12 Sampling Distributions

12.1 The Goal, and Fundamental Dilemma, of Statistics

Recall that the goal of statistics, at the most basic of levels, is to draw conclusions regarding the parameter values in a population of interest by analyzing a sample and computing statistics. Revisit Figure 10.1 for a visual representation of this procedure. In Chapter 11 we discussed in depth the study of descriptive statistics. Descriptive statistics aim to describe the data that have been observed through the study, through the computation of sample statistics or similar graphical procedures. That is, using the techniques from descriptive statistics we can take a sample and derive statistics from it. The fundamental dilemma we are faced with, however, is that a statistic will not typically equal a parameter value exactly. That is, the value we compute using a sample for any property¹ will not equal the value that the same property would take on in the population. As a result, while descriptive statistics allow us to understand thoroughly the data that we have collected, they do not (alone) address the complete goal of statistics.

To complement descriptive statistics we wish to be able to make statements about how sample statistics relate to, or are connected to, parameter values. In order to do so it is worth asking “why do the values of statistics tend to differ from the values of the corresponding parameters?”. Intuitively, the issue we are faced with is that a sample does not include every element of the population. As a result, quantities computed on a sample will differ from the same quantities computed in the population owing to the different make-up of the sample. We could envision what would happen if we took a second, different sample from the same population. We would likely get different elements in the sample, and as a result, anything computed on the sample would differ from the first time. If we continued to take samples, compute the values, and compare them we would find that each sample is subtly different from every other, leading to the values of statistics moving around sample-to-sample. Of course, if we could access the full population, the value of the parameter would never change since there is only one, true value. These differences sample-to-sample are referred to as sampling variability, and explain the core reason why statistics and parameters differ from one another.

Definition 12.1 (Sampling Variability) Sampling variability refers to the variation that occurs between samples drawn from the same population (whether the same method for selection is used or not). This variability manifests itself in the values of statistics that are computed on a sample, where repeated sampling from the same population will result in different values for the statistics. This variability is inherent in the sampling process and emerges owing to the fact that each sample will consist of different elements from the same population.

To understand this procedure completely, consider the following population of squares, depicted visually. If we had access to this entire population we would be able to determine any parameter value that we would like to know about, for instance, understanding the proportion of black squares present (in the population this results in a proportion of 0.195).

Figure 12.1: The population of squares. Consider each colour to represent a trait or variable for each individual in the population.

Generally, we will be unable to observe an entire population, and instead would be required to take random samples. If we take samples of size \(10\) from the population we may end up with something like the following.

Figure 12.2: A single sample from the population. In this sample of size \(10\), \(2\) of the resulting squares are black, making the sample proportion \(0.2\).

This sample, however, was not the only sample that we could have seen. Consider the following \(16\) samples. In each of them the number of black squares (and thus the proportion of black squares) differs. These differences arise naturally based on which squares happened to be included in the sample, and those that happened to be ignored. If we continued to sample more and more from the population and work out the corresponding proportion of black squares observed, we would see the proportions continue to vary.

Figure 12.3: Sixteen samples from the population. Each sample exhibits a different proportion of squares which are black, and as a result, a different sample proportion. Because this proportion differs from sample-to-sample we say that it is subject to sampling variability.

Owing to sampling variability, every time that we take a sample we expect to get a different value for our statistic. Because of this we can often regard the value of the statistic as being random. Ultimately, if the members of our sample determine the value of our statistic, and the members of our sample are randomly selected, then we know that the value of our statistic is a random value. Any numeric quantity which takes on random values is referred to as a random variable (Definition 5.1) and as a result statistics are random variables. Because statistics are random variables we must also conclude that statistics have distributions. The distribution of a statistic is referred to as the sampling distribution for the statistic, and serves as the primary tool for understanding how well the values of statistics and parameters agree with one another.

Example 12.1 (Sadie, Charles, and Ketchup) Sadie and Charles get along quite well in most regards, however, they cannot agree at all on ketchup. Specifically, Charles finds ketchup to be repugnant, disliking even being in its presence. Sadie, on the other hand, finds it to be quite pleasant and will happily enjoy it alongside many dishes. This is a frequent point of contention for them. As a result, they decide that they should take a survey of the individuals at their favourite coffee shop to settle the debate once-and-for-all. Thus, they go around asking each individual their thoughts on ketchup.

In the population as a whole, the number of people who like ketchup is best described by what distribution? What is the parameter of interest for Charles and Sadie?
If it is found that more people in the coffee shop agree with Charles than with Sadie, does that mean that more people in the population dislike ketchup? Explain.

Solution

The population distribution should be approximately binomial. The relevant parameter will be \(p\), the probability of “success”. Here \(p\) can either represent the proportion of individuals who like (or dislike) ketchup, depending on the ways in which the questions were phrased.
No, not necessarily. Because of sampling variability, it is possible to have selected a sample that shows a much different proportion than the true proportion in the population. It may be the case that it is close, or that it is far off. However, the general procedure of computing a statistic on a population is random and as such, the variation needs to be accounted for when drawing conclusions.

12.2 Sampling Distributions

Definition 12.2 (Sampling Distribution) A sampling distribution is the distribution of a sample statistic. The sampling distribution arises due to sampling variability, rendering samples – and statistics computed using samples – random.

The fact that statistics are random variables is the critical realization that facilitates inferential statistics. However, this is a concept which is not always immediately clear. It is worth reemphasizing how sampling distributions emerge, and how they differ from both frequency (or data) distributions, and from the underlying population distributions. We first consider a population. In this population the trait of interest will differ between individuals, and these differences will be summarized by a relevant parameter. When populations are large² we can view the trait in the population as being randomly distributed. We are thinking that, if we were to observe a single individual from the population, their value of the trait would follow some distribution. We call this underlying distribution the population distribution. Our interest is ultimately in the population distribution.

We can then think of taking a random, finite sample from the population. We can measure the value of the trait for all individuals in the sample. These observations constitute an observable dataset. Within these data we can discuss the frequency distribution or the data distribution, which summarizes how often values of the trait occurred in the sample. The data distribution describes what we actually observed, and we can characterize it exactly. We hope that our sample was a good sample³ and as a result, we hope that the data distribution is similar to the population distribution. However, we do not expect that these distributions will coincide directly since our sample is a subset of the population, meaning many values have been excluded. Using this sample we are able to compute statistics that are the sample version of the parameters of interest. These statistics characterize the data distribution in a similar way to the parameters characterize the population distribution.

We can then imagine repeating this process of sampling many times. Each time we do we would receive a slightly different sample, which in turn produces a slightly different data distribution, and as a result a slightly different statistic value. Suppose that we recorded the value of the statistic each time that we took our sample, and then re-sampled again. Doing this over and over again would produce a set of values for the statistics. These values would be seen as specific realizations from the distribution of possible realizations of the sample. This distribution is the sampling distribution. The sampling distribution characterizes the random variability in the value of a sample statistic, had we been able to repeatedly compute this over many different samples. The more spread that is in the sampling distribution, the more we expect different samples to differ from one another in terms of the value of the relevant statistic.

Consider the previous example of sampling squares from the population in Figure 12.1. If we continued to do this over, and over again, and we recorded the proportion of squares that were black, the resulting distribution would be the sampling distribution of the proportion of black squares. Looking at this distribution we could then ask “given a single sample from the population, how likely are we to get a representative value for the sample proportion?” If this probability is high then we can be relatively confident that a sample will provide us with a useful guess to the true parameter value. If this probability is low, we cannot be sure that we are learning much from the sample.

Figure 12.4: The sampling distribution for the proportion of black squares in samples of size \(10\) from the population of coloured squares. This distribution can be thought to emerge from the process of repeatedly sampling from the population, computing the resulting statistic, and then recording those statistics into a dataset itself. Moreover, we can read the probabilities here as stating “the probability that the proportion of black squares in a sample of size \(10\) will take on \(x\) is \(y\).”

If the sampling distribution of a statistic were known exactly, then probabilities could be computed regarding that statistic in the same way as probabilities are computed for any random variable. In our example, for instance, if we took \(\rho\) to represent the sample proportion for a random sample of size \(10\), then we could claim that \[P(\rho = 0.2) \approx 0.3056561.\] Because we know the value of the population parameter, and because \(0.2\) is as close to \(0.195\) as a sample can get in a population of size \(10\), we can thus say that nearly \(31\%\) of samples will provide an estimate that is as close to the truth as is possible, given the sample size. If we instead consider \[P(0.1 \leq \rho \leq 0.3) \approx 0.7792981,\] and so nearly \(78\%\) of our samples should be within \(1\) of the closest sample value to the true population parameter. That is, we can use the sampling distribution to assess how reliable our statistic is as a proxy for the parameter value.

A major difficulty in the application of this procedure in practice is that typically we do not have the true population on hand to either directly compute the sampling distribution, or to know what the true parameter value should be. If we did have access to the full population we would not need to use samples in the first place. Despite these limitations, the sampling distribution is still the key tool in unlocking an assessment of reliability of statistics as proxies for parameters. By recognizing that the sampling distribution is inherently useful in explaining the random behaviour of statistics, all that remains is being able to connect the sampling distribution to the population distribution. Fortunately, we will often find that, even without knowing the specific sampling distribution, we can make definitive statements about the link between the sampling distribution and the population distribution, giving a bridge between statistics and the corresponding parameters.

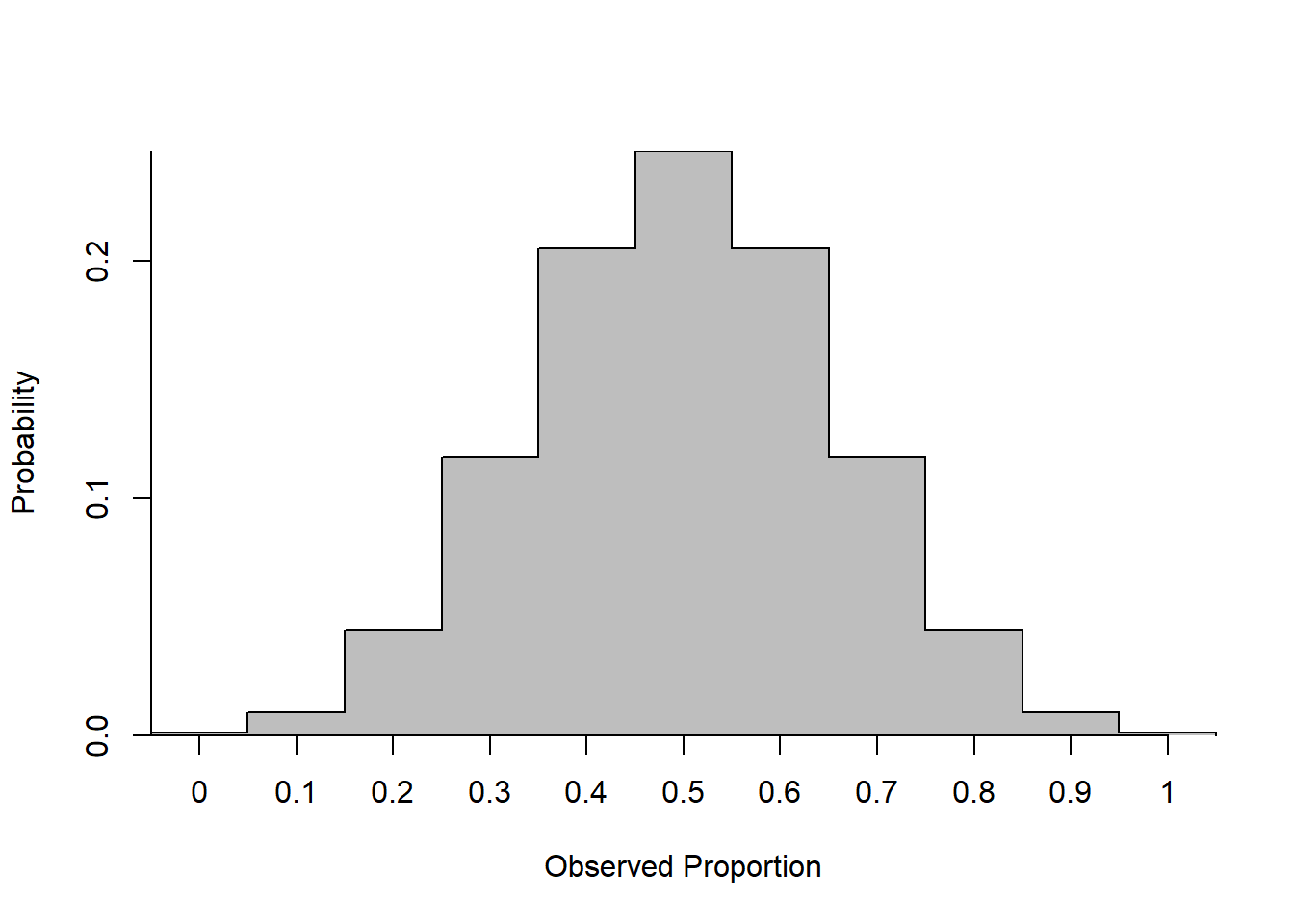
Example 12.2 (Sadie, Charles, and Ketchup (Repeated Over and Over)) After recognizing the lack of scientific validity of their single sample, Charles and Sadie decide that they should repeat their survey many times over. Each time they gather a sample of individuals and ask whether they agree with Charles or Sadie more. They do this many, many times, and report the proportion of individuals who agree with Sadie in the following chart.

How is this graph related to the data distribution? The population distribution? The sampling distribution?
According to this graph, what is (approximately) the probability that in a sample they will find more people agreeing with Sadie?
What conclusions can be drawn?

Solution

This graph shows the sampling distribution of the proportion of individuals who like ketchup in samples at random from the population. The population distribution would be binary, with everyone being either a \(1\) or a \(0\), however, the proportion in the \(0\) category should be related to the proportions realized in this graphic (so, around a 50-50 split). The data distribution would be comprised of observations from a single sample, where individuals in that sample were split at \(1\) and \(0\) as well. These observations would give rise to a single proportion displayed here.
According to the graph it appears that the data are split roughly 50-50 with proportions above and below \(0.5\). That is, it seems about equally likely that in a sample of individuals more people agree with Charles or more people agree with Sadie.
While drawing any definitive conclusions here is challenging from the graphic alone, owing to sampling variability, it seems likely that we could suggest that there is not a strong preference one way or the other in the population. If there were we would expect that more proportions would end up falling in favour of either Charles or Sadie, rather than the equal split that we actually observe.

12.3 The Sampling Distribution of a Sample Mean

As an illustrative example demonstrating the connection between the sampling distribution and the population distribution we will consider the case of sample means. Note that sample means are among the most important statistics that are worked with and so this example is representative of a large quantity of statistics in practical use. Moreover, statistics like sample proportions can be thought of as the sample mean of binary data.⁴ Other statistics can be analyzed in a similar manner, allowing us to draw similar conclusions for other parameters of interest.

12.3.1 Characterizing the Sampling Distribution of the Sample Mean

Consider an arbitrary population distribution for some trait. Suppose that \(X\) is a random variable that is drawn from this population distribution, so that the mean in the population is \(E[X]\) and the variance in the population is \(\text{var}(X)\). We will typically denote \(E[X] = \mu\) and \(\text{var}(X) = \sigma^2\), as we did for normal populations. Now, if we consider drawing a sample of size \(n\) from this population, and if we suppose that these are drawn independently of one another, then our sample can be thought of as a collection of \(n\) independent and identically distributed (Definition 5.12) random variables, denoted \(X_1, X_2, \dots, X_n\). Each of these random variables will have mean \(\mu\) and variance \(\sigma^2\), and each is independent of all the others. Then, the sample mean of this hypothetical sample is given by \[\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i.\] Note that we are using the same notation we used for random variables where capital letters indicate a random quantity, and the corresponding lowercase letters represent a specific value. Thus, \(\overline{X}\) is thought of as a random variable which represents the sample mean for a random sample. If we actually take a sample and compute the mean, we would have a corresponding \(\overline{x}\), which is just one realization of the random variable \(\overline{X}\).

Since \(\overline{X}\) is random it has a distribution. Because it is a statistic, its distribution is a sampling distribution, and in particular it is the sampling distribution of the sample mean. The specific form of this distribution will not generally be known, however, we can ask questions regarding parameters of this distribution (that is, sampling distribution parameters). Specifically, we may ask ourselves whether it is possible to determine \(E[\overline{X}]\) and \(\text{var}(\overline{X})\). Note that these are not the same as \(E[X]\) and \(\text{var}(X)\), where the former are the parameters of the sampling distribution and the latter are the parameters of the population distribution.

The Mean and Variance for the Sampling Distribution of the Sample Mean

Using the properties of expectation and variance of independent and identically distributed samples discussed in Section 7.5, we can claim that no matter the population distribution, \[E[\overline{X}] = \mu \quad\text{ and }\quad \text{var}(\overline{X}) = \frac{\sigma^2}{n}.\] That is, the mean and variance of the sampling distribution of the sample mean correspond to the mean of the population distribution and the variance of the population distribution scaled by the sample size, respectively.

Practically this means that the sample mean is centered on the true population mean, and on average should be correct. Moreover, the variance of the sample mean is related to the variance in the population⁵ and is inversely related to the sample size. The relationship to the sample size gives a mathematical justification for the intuition that “larger samples are preferable.” It makes sense that if your sample size is larger, you will get a better estimate of the truth. This can be justified since, as the sample size grows, the variance of the sampling distribution shrinks, and the sampling distribution becomes more heavily concentrated around the true population mean. It is constructive to consider what happens to the variability in the sampling distribution as the sample size increases \(n\to\infty\).

Specifically, as the sample size grows more and more, the variance shrinks smaller and smaller. Eventually, in the limit, the variance will shrink all the way to \(0\). At this point, we will be left with a sample mean that is exactly equal to the population mean, since \(E[X] = E[\overline{X}]\) and the variance of \(\overline{X}\) is zero. Of course, if we could take an infinite sample we would have taken every member of the population into the sample, and so we should expect that the two align in that case. Now, it will never be the case that we have a truly infinite sample, and so there will always be some variability that remains in the sampling distribution. However, the reduction in variance occurs even at finite samples. As more and more members are included in the sample, there is less and less variability in the statistic, and the results become more and more concentrated around the true population value. The important point of this characterization is that it does not matter what the population distribution is, nor what the value for the sample mean is.

More often than not when discussing the variability of the sampling distribution the measure of choice will be the standard deviation rather than the variance. That is, instead of reporting that \(\text{var}(\overline{X}) = \dfrac{\sigma^2}{n}\), it is far more common to report that \(\text{SD}(\overline{X}) = \dfrac{\sigma}{\sqrt{n}}\). These two quantities hold the same information, and it is straightforward to move from one to the other by either taking the square root or squaring the quantity. Now, when the standard deviation is computed for a statistic, such as the sample mean, it is not typically referred to as a standard deviation. Instead, it is called a standard error.

Definition 12.3 (Standard Error (of a statistic)) For any statistic \(\widehat{\theta}\) the standard error of the statistic is given by its standard deviation. That is, \[\text{SE}(\widehat{\theta}) = \text{SD}(\widehat{\theta}).\]

Definition 12.4 (Standard Error (of the Sample Mean)) The standard error of the sample mean (SEM) is the standard error of \(\overline{X}\). For a population with variance \(\sigma^2\), this is given by \[\text{SE}(\overline{X}) = \frac{\sigma}{\sqrt{n}}.\]

The standard error is a useful metric since, if reported alongside the estimate, we can directly quantify the uncertainty of the statistic. A higher standard error equates directly to more uncertainty in the statistic and this uncertainty is measured on the same scale as the statistic itself. Now, in practice, you will not have an exact value for the standard error since it relies on knowledge of \(\sigma\). Still, it will often be the case that we can get a good sense as to the standard error via the sample standard deviation, and use this quantity in place.⁶

Example 12.3 (Charles and Sadie Visit the Zoo) One day Charles and Sadie decide to visit the local zoo (a zoo with a strong focus on conservation research). Charles and Sadie learn that:

Eastern lowland gorillas weigh on average around \(407\)lbs, with a standard deviation of approximately \(65\)lbs.
Sumatran elephants weigh on average around \(6600\)lbs, with a standard deviation of approximately \(750\)lbs.
Leatherback sea turtles weigh on average around \(1036\)lbs, with a standard deviation of approximately \(125\)lbs.

Charles and Sadie think about finding samples of \(16\) of each of these species in the wild.

Characterize the sampling distribution for each of the species.
If larger samples were taken, how would this change the mean and standard error of the sampling distributions?
Suppose a sample of size \(n\) is taken of leatherback turtles. How large of a sample of Sumatran elephants would be needed to have the same standard error of the sample mean?

Solution

For the gorillas, the sampling distribution will be characterized by a mean of \(407\) and a variance of \(\dfrac{65^2}{16} = 264.0625\). The standard error is given by \(\dfrac{65}{\sqrt{16}} = 16.25\). For the elephants, the sampling distribution’s mean will be \(6600\) with a variance of \(35156.25\) and a standard error of \(187.5\). Finally, the sea turtles will have a sampling distribution characterized by a mean of \(1036\) with a variance of \(976.5625\) and a standard error of \(31.25\).
No matter the sample size, the mean of the sampling distribution does not change. As the sample size increases, however, the standard error will decrease. As a result, we would expect less variability in the sampling distribution with larger samples compared to the sampling distribution with smaller samples.
Suppose \(n_2\) elephants are sampled. The standard errors are given by \(\dfrac{125}{\sqrt{n}}\) and \(\dfrac{750}{\sqrt{n_2}}\), respectively. Thus, we get \[\begin{align*} \frac{125}{\sqrt{n}} &= \frac{750}{\sqrt{n_2}} \\ \sqrt{n_2} &= 6\sqrt{n} \\ n_2 &= 36n. \end{align*}\] As a result, you would need to sample \(36\) times as many elephants as you did turtles to have the same standard error.

Chebyshev’s Inequality and Bounds on the Sampling Distribution of the Sample Mean

Suppose that the population variance is known but that the population mean is unknown. Moreover, the population distribution is unknown. In this case, we can still apply Chebyshev’s inequality to make probability statements regarding the likelihood that \(\overline{X}\) is close to \(\mu\). Recall that Chebyshev’s inequality states that, for a random variable \(X\) with mean \(\mu\) and standard deviation \(\sigma\), \[P(\mu - k\sigma \leq X \leq \mu + k\sigma) \geq 1 - \frac{1}{k^2}.\] Suppose then that we consider the sample mean, \(\overline{X}\) to be the random variable of interest. The standard deviation of \(\overline{X}\) is \(\text{SE}(\overline{X}) = \sigma/\sqrt{n}\). Then, if we take \(\delta\) to be some positive value, we can state that the probability that \(\overline{X}\) is within \(\delta\) of \(\mu\) is at least, \[P(\mu - \delta \leq \overline{X} \leq \mu + \delta) \geq 1 - \frac{\sigma^2}{\delta^2n^2}.\] This will hold for any positive value of \(\delta\).

If we take \(\delta = 2\dfrac{\sigma}{\sqrt{n}}\), for instance, then we will find that the probability that the sample mean is within two standard errors of the true population mean is at least \(0.75\). That is, no matter the distribution of the population, there is always at least a \(0.75\) chance that the sample mean will be within two standard errors of the truth. This gives further justification for reporting the standard error.

12.3.2 The Sampling Distribution of the Sample Mean in Normal Populations

While it is possible to make concrete statements regarding the relationship between the parameters of the sampling distribution and the population distribution, we are not able to make concrete probability statements regarding the sample mean in general.⁷ However, in certain cases we are able to make stronger statements regarding the sampling distribution. These statements stem from knowledge that we may have of the underlying population. While it may be unrealistic to make strong assumptions regarding the values of population parameters, it is often the case that we may have a general idea of the shape of the underlying distribution. In Chapter 8 and in Chapter 9 we discussed how certain named distributions emerge as a result of the underlying processes, and how these can be identified based on the particulars of a given scenario. If you are in a case where you are willing to make an assumption regarding the shape of the population distribution, it may be possible to make stronger statements regarding the sampling distribution.

The most common assumption to make regarding an underlying population distribution is that the population is (approximately) normally distributed. That is, we assume that \(X \sim N(\mu,\sigma^2)\), where we perhaps have no knowledge as to what the values of \(\mu\) or \(\sigma^2\) are. Making this assumption regarding the shape of the distribution allows us to fully characterize the sampling distribution of \(\overline{X}\). To do so, we need only revisit the closure properties of the normal distribution. Specifically, if we have multiple quantities which are independent of one another, and each of them follows a normal distribution, then the sum of these random quantities will also follow a normal distribution. In addition, if we have a normally distributed random variable, and we multiply it by a constant, then the result will still be a normally distributed random variable.

The sample mean is constructed by first taking a sum of a set of random variables, and then second multiplying this summation by \(\dfrac{1}{n}\). If the population is normally distributed then this is the sum of a set of normally distributed random variables, and as a result, will be normally distributed itself. That is, whenever the population distribution is normally distributed, the sampling distribution of the sample mean will also be normally distributed.

The Sampling Distribution of the Sample Mean in Normal Populations

Suppose that a population is normally distributed with mean \(\mu\) and variance \(\sigma^2\). Then, supposing a random sample is taken independently, giving \(X_1,\dots,X_n\), the sampling distribution of the sample mean will be such that \[\overline{X} \sim N(\mu, \frac{\sigma^2}{n}).\]

In these cases, it is possible to make more concrete statements regarding the behaviour of the sample mean. For instance, an application of the empirical rule tells us that in approximately \(95\%\) of cases, the sample mean will be within two standard errors of the true mean. Supposing that the population variance is not too large, or the sample size is sufficiently large, this gives reasonable certainty that the sample mean is a good proxy for the population mean. Using this result to make definitive probability statements still requires knowledge of \(\sigma^2\) in the population, which will often be an unrealistic assumption. In the coming chapters we will learn how to overcome this shortcoming and quantify the uncertainty in the values of statistics even without direct knowledge of the population variance. A more pressing question, however, is whether there are any strong statements that can be made about the distribution of the sample mean when the population is not normally distributed.

Example 12.4 (Charles and Sadie Consider their Zoo Trip) After returning from the zoo, Charles and Sadie wish to figure out whether the zoo appeared to have a good representation of the animals or not. They record all of the following information:

Eastern lowland gorillas weigh on average around \(407\)lbs, with a standard deviation of approximately \(65\)lbs. The zoo had \(4\) gorillas with an average weight of \(342\)lbs.
Sumatran elephants weigh on average around \(6600\)lbs, with a standard deviation of approximately \(750\)lbs. The zoo had \(25\) elephants with an average weight of \(6750\)lbs.
Leatherback sea turtles weigh on average around \(1036\)lbs, with a standard deviation of approximately \(125\)lbs. The zoo had \(64\) turtles, with an average weight of \(1030\)lbs.

In order to proceed, Charles and Sadie are willing to assume that the animals all have weights that are approximately normally distributed in the population.

Describe the sampling distributions for each animal from the zoo.
If the sample of gorillas is randomly selected from the wild, what is the probability that the zoo would have a sample weight as low (or lower) as what they have?
If the sample of elephants is randomly selected from the wild, what is the probability that the zoo would have a sample weight as high (or higher) as what they have?
If the sample of turtles is randomly selected from the wild, what is the probability that the zoo would have a sample weight between \(1020.375\) and \(1051.625\)?

Solution

Because the populations are normally distributed all of the sampling distributions will be normally distributed as well. Let \(G\), \(E\), and \(T\) represent the random variables corresponding to gorillas, elephants, and turtles respectively. Then \[\begin{align*} \overline{G} &\sim N\left(407, \frac{4225}{4}\right) \\ \overline{E} &\sim N\left(6600, \frac{562500}{25}\right) = N\left(6600, 22500\right)\\ \overline{T} &\sim N\left(1036, \frac{15625}{64}\right). \end{align*}\]
Since the sampling distribution is normal we can compute this as \[\begin{align*} P(\overline{G} \leq 342) &= P(\frac{\overline{G} - 407}{\sqrt{4225/4}} \leq \frac{342 - 407}{\sqrt{4225/4}}) \\ &= \Phi\left(-2\right) \\ &\approx 0.025. \end{align*}\] The final approximation stems from an application of the empirical rule.
As above, we can take \[\begin{align*} P(\overline{E} \geq 6750) &= 1 - P(\overline{E} \leq 6750) \\ &= 1 - P(\frac{\overline{E} - 6600}{\sqrt{22500}} \leq \frac{6750 - 6600}{\sqrt{22500}}) \\ &= 1 - \Phi(1) \\ &\approx 0.16. \end{align*}\]
For the turtles we get \[\begin{align*} P(1020.375 \leq \overline{T} \leq 1051.625) &= P(\frac{1020.375 - 1036}{\sqrt{15625/64}} \leq \frac{\overline{T} - 1036}{\sqrt{15625/64}} \leq \frac{1051.625 - 1036}{\sqrt{15625/64}}) \\ &= \Phi(1) - \Phi(-1) \\ &\approx 0.68. \end{align*}\]

12.3.3 The Central Limit Theorem

If the underlying population does not follow a normal distribution it will not be the case that the sampling distribution is exactly normally distributed. However, a remarkable result states that, while we cannot state that a normal distribution will be exactly correct for the sampling distribution, we can state that, in large enough samples, the normal distribution will be approximately correct for the sampling distribution. That is to say, no matter the population distribution, if the sample size is large enough, the sample mean will have a distribution that is approximately normal. This statement is known as the Central Limit Theorem, and it sits at the heart of many of the results we will leverage for inferential statistics.

The Central Limit Theorem (CLT)

Suppose that \(X\) is drawn from a population with mean \(\mu\) and variance \(\sigma^2\), but an otherwise unspecified distribution. If a sample of size \(n\) is drawn from this population, giving \(X_1,\dots,X_n\), then supposing that \(n\) is large enough, we will have that \[\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i \dot\sim N(\mu, \frac{\sigma^2}{n}),\] where \(\dot\sim\) means “is approximately distributed as”. More formally, we can state that as \(n\to\infty\), the distribution of \(\overline{X}\) converges to a normal distribution.

The power of this result is difficult to overstate. Simply put, if \(n\) is sufficiently large then we do not need to know anything about the underlying population distribution in order to make use of the results from the normal distribution in assessing its behaviour. No matter the underlying population we can calculate using normal probabilities, make use of the empirical rule, and make definitive statements like those in the previous section. Importantly, these probabilities will not be exactly correct, however, even for moderate large \(n\), they will likely be close enough to be very useful. A natural question regarding the application of the Central Limit Theorem is then how large does \(n\) have to be? The short answer is that it depends. The required sample size for \(n\) depends primarily on how close to normality the original population is. If you have a population that is approximately normal to begin, even very small sample sizes will suffice for approximate normality. If the original population is further from normality then it will take larger samples to apply the CLT.

This plot shows the convergence of the sampling distribution of the sample mean to the normal distribution for three different populations. In the top row the population distribution is shown, followed by the sampling distribution for the sample mean over increasing values of n. While all three end up following a normal distribution, and all three end up having very little variance as the sample size grows (the x-axes are held constant across all plots), we can see that normality emerges more quickly for the populations that are closer to normality to begin. — This plot shows the convergence of the sampling distribution of the sample mean to the normal distribution for three different populations. In the top row the population distribution is shown, followed by the sampling distribution for the sample mean over increasing values of \(n\). While all three end up following a normal distribution, and all three end up having very little variance as the sample size grows (the \(x\)-axes are held constant across all plots), we can see that normality emerges more quickly for the populations that are closer to normality to begin.

Often, the concrete advice will be that, if \(n \geq 30\), the CLT will apply. As with most hard-and-fast rules, I would advise against following this dogmatically. The issue is two-fold. First, if populations are near to normality then the CLT will likely provide a suitable approximation for much smaller \(n\) than \(30\). Second, and more concerning, if the initial population is sufficiently far from normality it may require substantially larger sample sizes for the sampling distribution to appear normal. Instead of using a definitive, arbitrary cutoff, it is more sensible to consider the problem at hand, the likely shape of the population, and the sensitivity of your conclusions to the assumption that the CLT Is a good approximation. While it is hard to establish a clear-cut rule, it is always the case that as \(n\) increases in size the approximation becomes more and more reasonable. Throughout these course notes we will endeavour to make clear whenever the sample size is “large enough” for the CLT to hold. When in doubt, taking \(n\geq 30\) provides a useful starting point.

Example 12.5 (Charles and Sadie Re-Consider their Zoo Trip) After working out the probabilities associated with their zoo trip and the likelihood of observing what they observed (Example 12.4), Charles and Sadie do some additional research. They learn that their assumptions around the normally distributed weights of the animals likely do not hold. Instead, they learn that

The weights of gorillas are far from normal, with different modes emerging depending on various factors around the gorilla. The zoo had a sample of size \(4\).
The weights of elephants are close to normal, but not exactly so – there is more variability than would be expected in a normal population. The zoo had a sample of size \(25\).
The weights of sea turtles are far from normal, exhibiting skewness and multi-modality. The zoo had a sample of size \(64\).

Which of the conclusions that Charles and Sadie have previously drawn are still justified? Why and how?
Which of the conclusions that Charles and Sadie have previously drawn are no longer justified? Why?

Solution

Concluding that the sampling distribution for the sample mean weight of elephants is normally distributed is likely still justifiable. This is because the sample size (\(25\)) is likely large enough to invoke the CLT, meaning that the sampling distribution will be approximately normally distributed. This is justifiable since the population is approximately normal. Concluding that the sampling distribution for the sample mean weight of sea turtles is approximately normal is also likely justifiable. This is because, despite the fact that the population distribution is far from normal, the sample is large enough (\(64\)) to invoke the CLT. The distributions here will not be exactly normal, however, they will be close enough to use it as an approximation.
Concluding that the sampling distribution for the sample mean weight of the gorillas is normal is no longer justified. Because the sample size is very small (\(4\)) we cannot use the CLT. As a result, we would rely on the population distribution being normal in order to use normal probabilities; however, in this case, the population is far from normal, invalidating the assumption.

12.4 Exploring Sampling Distributions in R

The fact that the sampling distribution is best interpreted as the distribution that arises from repeatedly computing a particular statistic renders statistical programming to be an effective tool for exploring the ideas associated with sampling variability and sample statistics. If the population distribution is known, then it is possible (using the previously discussed tools for drawing samples from named distributions) to work out empirically the sampling distribution for any statistic. Moreover, we can use R to determine the necessary sample sizes in order for the sampling distribution of the sample mean to appear approximately normal. The process in all of these cases is similar: we repeatedly sample from the population distribution, compute the estimated statistic, and then record this value. Then, we can plot the sampling distribution by plotting the result of the various estimates.

The results of this first experiment demonstrate that, if the population is exponentially distributed, a sample of size \(10\) is insufficient to approximate normality. Consider what happens as you increase the sample size to the shape of the histogram. We can also see that the approximated mean and variance are close to what we would theoretically expect them to be, namely \(\dfrac{1}{4}\) and \(\dfrac{1}{160}\). If the number of replicates were increased, these values should become closer to the truth.

Perhaps more useful than considering the sampling distribution of the sample mean, however, is the use of statistical software to consider the sampling distributions of other statistics. Try to determine how you may modify this code to look at the sampling distribution for the sample variance, or the sample median, or the sample minimum, or any other statistic that can be computed on a sample. The following code will do just that for a normally distributed population.

The use of these simulations to determine the sampling distribution is an incredibly powerful tool in statistics. It allows us to work with quantities practically, even when the theory is too cumbersome to derive. What is more, the same ideas can be extended to approximate sampling distributions even when the population distribution is not known at all. The process is called bootstrapping, and it is one of the most powerful ideas that has been derived in modern statistics.

Be that a mean, variance, median, maximum, or so forth.↩︎
In small populations the same general procedure still applies, however, it will often be the case that in smaller populations we have a lesser need for deep statistical methodologies. Instead, we will be able to rely on census techniques or similar.↩︎
Meaning that it generally represents the underlying population.↩︎
To see this, consider the example of the population of coloured squares. For each square in our sample, record a \(1\) if the square is black and a \(0\) otherwise. Then, the sample mean \(\overline{x}\) is computed as \(\frac{1}{n}\sum_{i=1}^n x_i\). This is equivalent to the number of \(i\) that have \(x_i = 1\) divided by the total number, or put differently, the number of squares that are black divided by the total number of squares. In this sense, the proportion of black squares is a sample mean, and the ensuing discussion applies equally well to either case.↩︎
The more variability in the population the more variability in statistics computed from the population. This should make some intuitive sense. If a population is very concentrated in values, it does not really matter what sample you take as everyone will be close to one another, and most samples will be similar. If instead, the population has a lot of variability, then the specific sample will matter a great deal, and you will expect tremendous variability sample-to-sample.↩︎
Note, some authors refer to the standard error as the standard error using the sample standard deviation instead. That is, they define the standard error of the sample mean to be \(\dfrac{s}{\sqrt{n}}\) rather than \(\dfrac{\sigma}{\sqrt{n}}\). This has the benefit of being able to be computed, but the drawback of not being the true value of the standard deviation of the statistic. In these notes we will refer to this, where relevant, as the estimated standard error, and we will view this quantity as a guess at the true standard error.↩︎
We can lower-bound the probabilities using Chebyshev’s inequality, but this is not necessarily a useful lower bound.↩︎

12.1 The Goal, and Fundamental Dilemma, of Statistics

12.2 Sampling Distributions

12.3 The Sampling Distribution of a Sample Mean

12.3.1 Characterizing the Sampling Distribution of the Sample Mean

12.3.2 The Sampling Distribution of the Sample Mean in Normal Populations

12.3.3 The Central Limit Theorem

12.4 Exploring Sampling Distributions in R

Self-Assessment