18  The Analysis of Categorical Data

18.1 Contingency Tables, Frequency Distributions, and Categorical Data

The concept of contingency tables (Definition 4.7) was introduced in Section 4.5. Briefly, contingency tables succinctly summarize the breakdown of two (or more) traits in a population. The numbers of individual items in the population that satisfy the intersecting traits are recorded in a table, with each member of the population counted at some specific intersection. Contingency tables provide an effective tool for considering probability distributions over finite populations. This is particularly true when the traits being considered are categorical.

Categorical data provide an interesting challenge for statistical inference. If collected data happen to be categorical, it may not be immediately clear how to analyze them. With quantitative measurements we can readily compute estimates that map onto specific parameters in the population distribution. The parallels with categorical data are less direct.1 In order to conduct inference using categorical data, we require a technique for systematically converting qualitative information into quantitative information. While it is conceivable to determine several strategies for this purpose, one highly effective tool is the use of frequency distributions (Definition 11.1).

Notably, a contingency table can be seen as a method of encoding the joint frequency distribution of two (or more) categorical factors in a sample. By simply recording the number of individuals who possess particular combinations of traits, we are able to have a succinct breakdown of the composition of the sample. This summarizes the categorical features of the sample, but it does so quantitatively. Using the frequency distribution it is possible to ask whether different traits occur with similar frequencies in the sample.2 Alternatively, frequency distributions can begin to give insight into whether different traits are related to, or independent of, one another.3

Thus, (joint) frequency distributions, often expressed via contingency tables for samples, provide a useful mechanism for summarizing categorical data, and can in turn be used to conduct statistical inference. The primary technique for doing so is to consider what was expected to be seen based on an underlying null hypothesis, and then assess how different what was actually observed happened to be. In a sense we are comparing the observed contingency table to an expected contingency table, and the similarity (or difference) dictates the likelihood that our hypothesized model can adequately explain the data.

18.2 Expected Cell Counts for Contingency Tables

When dealing with random variables (Definition 5.1), the concept of an expected value was explored. The idea was that we can answer the question “What value do we expect to observe, if this random variable were to be realized?” on the basis of the underlying probability distribution. We can ask, and answer, a similar type of question in terms of contingency tables. Suppose, for instance, that we roll a die that has six different colours printed on each of its sides. If we roll the die \(60\) times it is reasonable to ask ourselves “how many times do we expect to see each colour?”. If the die is fair then we should expect that no colour turns up any more often than any other, and as a result, our expectation would be to observe \(10\) rolls for each colour. Now, suppose further that we did run this experiment. By recording the colours of the \(60\) rolls we could compare our observations to the expected observations, and the similarity of these two frequency distributions will give some evidence whether the die is actually fair or not. There is nothing particularly special about assuming the die is fair to determine the expected counts.

More generally, if we pose any particular model underpinning reality, we can determine what we would expect to observe in a frequency distribution or contingency table. This may be achieved by imposing a particular distribution on the underlying population or through assumptions about the traits of the population that impact their distribution. Critically, we require the ability to translate these types of statements into expected values for the contingency table and frequency distribution. While any set of assumptions that generate expected values can be used, there are three common overarching types of assumptions that are worth considering directly in more depth. Namely, these are (i) the fit of a specific distribution, (ii) homogeneity of multiple populations, or (iii) independence of two characteristics.

18.2.1 Expected Values for Goodness-of-Fit

It is common to ask whether a particular distribution is a good fit for a particular set of data. This may be through named distributions4 or it may be through explicitly specified distributions. In either case, these distributions give rise to expected frequency distributions. The idea, in brief, is to leverage the specific distribution to theoretically determine the expected number of observations in each cell, based on the overarching total. This was the process used by assuming that the die was fair. This assumption amounted to an assumption that the population follows a discrete uniform distribution (Section 8.1), and could be used to determine the expected counts.

Instead of assuming that the distribution was a discrete uniform, perhaps we had an explicitly specified distribution. Suppose that we wondered whether the die was biased such that it was \(5\) times as likely to come up as the \(6\)th colour, compared to all other options. Then, taking \(p_i\) to be the probability that the \(i\)th colour is rolled, we can determine that \(p_1 = p_2 = p_3 = p_4 = p_5 = 0.1\), while \(p_6 = 0.5\). Then, if we still rolled the coin \(60\) times we should expect to see \(E_1 = E_2 = E_3 = E_4 = E_5 = 0.1(60) = 6\), while \(E_6 = 0.5(60) = 30\). Any other explicit assumptions about the relative proportions of the different categories would result in a corresponding set of expected frequencies.5

In general, by assuming an underlying distribution, we can determine the theoretical probability of a particular observation being observed in a particular category. Then, with this probability, say \(p\), the expected count in a cell is given by \(np\), where \(n\) is the total number of observations in the frequency distribution or contingency table.

The Expected Value for Goodness-of-Fit Testing

Suppose that a distribution is hypothesized regarding the frequency distribution for a particular trait. Namely, suppose that the distribution gives rise to a set of probabilities, \(\{p_1,p_2,\dots,p_k\}\), such that each option for the trait \(j=1,\dots,k\) will have probability \(p_j\) of being observed. Moreover, suppose that a total of \(n\) observations will be taken. Then, the expected value of the \(j\)th cell is \(E_j = np_j\).

If the cell probabilities are not given directly, such as through a probability mass function or similar, they can often be derived via the use of a cumulative distribution function. Notably, if the categories are bins of numeric quantities, then, for a given continuous distribution with cumulative distribution function \(F\), \[E_j = n(F(u_j) - F(\ell_j)),\] where \(u_j\) is the upper bound on the \(j\)th bin, and \(\ell_j\) is the corresponding lower bound.

18.2.2 Expected Values for Homogeneity

If we wish to describe two quantities as being alike, we frequently describe them as being homogenous. If some trait is homogenous between two populations, then that trait is equally distributed between those different populations. We may wish to understand, for instance, whether genders are represented homogeneously between various careers. Note that this is not to say that all careers are equally likely to be pursued, but rather, that the rate that individuals pursue various careers is the same across gender.

We are able to summarize the frequency distribution of a single trait6 across multiple populations7 using a contingency table. We take the characteristic that defines the populations as one of the factors (say the rows), and then the trait of interest as the other factor (say the columns). This summarizes data in a manner that is identical to taking a sample from a single population, measuring two different traits, but it is conceived of differently. Notably, we view this as multiple samples of a single trait, from multiple distinct populations. Denote the number of observations from population \(i\), who have trait \(j\) as \(n_{i,j}\). Each population will have a set number of realizations drawn from it, denoted \(n_{i, \bullet}\).8 We can use a similar notation to denote the number of observations with trait \(j\), taking \(n_{\bullet, j} = \sum_{i=1}^k n_{i, j}\).

Table 18.1: The notation used for a contingency table based on \(k\) distinct populations, with each of which categorizes individuals based on a single trait, with \(\ell\) possible values. The notation \(n_{i,j}\) gives the total number of individuals in population \(i\) with trait \(j\). Subscripts of \(\bullet\) are used to sum over an index, so \(n_{i,\bullet}\) is the total sample size from population \(i\), and \(n_{\bullet,j}\) gives the total number of individuals with trait \(j\).
Population 1 Population 2 \(\cdots\) Population \(k\) Total
Trait \(1\) \(n_{1,1}\) \(n_{2,1}\) \(\cdots\) \(n_{k,1}\) \(n_{\bullet, 1}\)
Trait \(2\) \(n_{1,2}\) \(n_{2,2}\) \(\cdots\) \(n_{k,2}\) \(n_{\bullet, 2}\)
\(\vdots\) \(\vdots\) \(\vdots\) \(\ddots\) \(\vdots\) \(\vdots\)
Trait \(\ell\) \(n_{1,\ell}\) \(n_{2,\ell}\) \(\cdots\) \(n_{k,\ell}\) \(n_{\bullet, \ell}\)
\(n_{1,\bullet}\) \(n_{2,\bullet}\) \(\cdots\) \(n_{k,\bullet}\) \(n\)

Thus, the total number of realizations will be \(n = n_{1, \bullet} + n_{2, \bullet} + \cdots + n_{k, \bullet} = n_{\bullet, 1} + n_{\bullet, 2} + \cdots + n_{\bullet, \ell}\). In order for the populations to be homogenous, we would expect that the proportion of observations for any trait, say \(\dfrac{n_{i,j}}{n_{i,\bullet}}\) should be equivalent across the various populations. Note that, across the entire sample, the proportion of individuals with trait \(j\) is \(\dfrac{n_{\bullet, j}}{n}\). Thus, if we take \[p_j = \dfrac{n_{\bullet, j}}{n},\] under a homogenous model for the populations we should observe that \(n_{i, j} = n_{i,\bullet}p_j = \dfrac{n_{i,\bullet}n_{\bullet,j}}{n}\).9

Formally, we estimate the overall proportion of individuals in the sample with each trait, combining them across the different populations. We then suggest that, if the populations are truly homogenous with respect to the given trait, we would expect to see the proportion of individuals with the given trait being equivalent across each population. This gives rise to the homogenous expected frequency.

The Expected Value for Homogeneity Testing

Suppose that we are considering \(k\) distinct populations, and hypothesize that these \(k\) populations will be homogenous with respect to some trait that has \(\ell\) distinct options. In this case, for the \(i\)th population and \(j\)th value of the trait, we should expect to see \[E{i,j} = \frac{n_{i,\bullet}n_{\bullet,j}}{n}.\] That is, the expectation is the total size of the \(i\)th population, multiplied by the total count of individuals with the \(j\)th trait, divided by the total number of individuals.

18.2.3 Expected Values for Independence

Suppose that, rather than drawing from \(k\) distinct populations, we take a sample from a single population but measure two different traits.10 In this framing it is natural to inquire whether the traits measured in the population are independent of one another. Recall that independence (Definition 4.5) arises whenever one event (or random variable) provides no information regarding another event (or random variable). Mathematically, events \(A\) and \(B\) are independent if \(P(A,B) = P(A)P(B)\), and random variables \(X\) and \(Y\) are independent if \(p_{X,Y}(x,y) = p_X(x)p_Y(y)\).11

Thus, suppose that a two-way contingency table exists, using the same notation as Table 18.1, however, this time representing draws from a single population with two different traits measured. Thus, \(n_{i,j}\) is the count of the number of individuals who have option \(i\) for the first trait \(1\) and option \(j\) for the second trait. Then, consider the event \(A\) to be that a randomly selected individual has \(i\) as their first trait, and the event \(B\) to be that a randomly selected individual has \(j\) as their second trait. Thus, \[P(A) = \frac{n_{i,\bullet}}{n}, \quad P(B) = \frac{n_{\bullet,j}}{n},\quad\text{and}\quad P(A,B) = \frac{n_{i,j}}{n}.\] If \(A\) and \(B\) are independent then, this would require that \[\frac{n_{i,j}}{n} = \frac{n_{i,\bullet}}{n}\times\frac{n_{\bullet,j}}{n} \implies n_{i,j} = \frac{n_{i,\bullet}n_{\bullet,j}}{n}.\]

The same logic applies to any combination of traits. As a result, if we hypothesize that two traits in a population are independent, this gives us a means of determining how many observations we should expect to see, in each cell.

The Expected Value for Independence Testing

Suppose that we are considering a single population, with two traits, the first of which has \(k\) options and the second with \(\ell\) options. Further, suppose we hypothesize that, in this population, these traits are independent of one another. In this case, for the \(i\)th option of trait one and \(j\)th value of trait two, we should expect to see \[E{i,j} = \frac{n_{i,\bullet}n_{\bullet,j}}{n}.\] That is, the expectation is the total number of individuals with \(i\) as the first trait, multiplied by the total count of individuals with the \(j\)th second trait, divided by the total number of individuals.

Note that the expected value for testing independence and the expected value for testing homogeneity are mathematically equivalent to one another. In a sense, the assumption of homogeneity is equivalent to the assumption of independence, and vice versa. The distinction, however, arises based on what the data represent and how the data arise. When we are considering independence, we are envisioning the sample as arising from one overarching population, and we take a random sample from this. When we are considering homogeneity, we are considering \(k\) distinct populations, with random samples from each of these. Practically, this means that in homogeneity testing, we have \(n_{i,\bullet}\) fixed for all \(i\), while in independence testing, \(n_{i,\bullet}\) is a random quantity that is only observed once the sample is realized. We should not expect to see the exact same contingency tables if we run two separate experiments, one randomly sampling from a combined population, and the other sampling from each population separately.12

18.3 Chi-Squared Tests

Categorical data are well-summarized using a frequency distribution.13 Concrete assumptions regarding the underlying distribution of any categorical traits give rise to expected frequency distributions. The comparison of these observed and expected tables give a natural method for testing the underlying assumptions. Specifically, the observed and expected frequency distributions naturally give rise to Pearson’s chi-squared test statistic. This test statistic, under some minimal assumptions, will approximately follow a chi-squared distribution, supposing that the hypothesis used to generate the expected distribution is correct. Thus, this setup can be used to test assumptions regarding the underlying distribution of the categorical data.

18.3.1 The Chi-squared Test Statistic

To express the test statistic, suppose that we make observations \(O_{i,j}\) across the contingency table, for \(i=1,\dots,k\) and \(j=1,\dots,\ell\). Moreover, suppose that, under the assumptions that are being tested, the corresponding expected cell counts are found to be \(E_{i,j}\). Then the chi-squared test statistic is given by \[\chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{\ell}\frac{(O_{i,j} - E_{i,j})^2}{E_{i,j}}.\] Note that, if instead of a contingency table, a frequency distribution is used, this can be reframed as having observations \(O_i\), for \(i=1,\dots,k\), with corresponding expectations \(E_i\). Then, in this setting, \[\chi^2 = \sum_{i=1}^k \frac{(O_i - E_i)^2}{E_i}.\]

In general, the test statistic is computed by finding \[\frac{(\text{Observed} - \text{Expected})^2}{\text{Expected}},\] for each cell in the contingency table or frequency distribution, and then summing all of these values. This test statistic does not depend on the underlying hypothesis that is being tested, only on being able to determine the expected quantities for each cell in the table or distribution.

18.3.2 The Null Distribution

Under the null hypothesis, that the expected values are actually correct, the chi-squared test statistic will have an (approximate) chi-squared distribution. There are two important caveats on this point:

  1. This approximation will only hold under assumptions on the sampling procedure, sample size, and expected cell counts; and
  2. The exact number of degrees of freedom for the chi-squared distribution will depend on the assumptions generating the expectations.

There are three primary assumptions required to conduct a chi-squared test. First, we must assume that the sample arises from simple random sampling. That is, there is an overarching population (or multiple populations in the case of testing for homogeneity), from which the observed data are drawn, with equal probability of any member of the population being sampled. If sampling is not done via a simple random sample, alternatives to the chi-squared procedure are required. Next, we require that the expected cell counts are all sufficiently large. As a general rule of thumb, all the expected cell counts should be above \(5.\)14 Note that this assumption puts an implicit requirement on the sample size. Namely, if your sample size is too small, the expected counts will not be large enough to adequately perform the hypothesis test. The final assumption that is required is that the observations in the sample are independent of one another. We need to make independent draws from the underlying population, rather than allowing for dependence between different observations.15

If the assumptions are all satisfied, then \(\chi^2 \stackrel{H_0}{\sim} \chi^2_{d}\), where \(d\) represents the number of degrees of freedom for the distribution. Broadly speaking, the degrees of freedom will be given by \(k\ell - c\), where \(k\) and \(\ell\) are the total number of options for traits one and two, and \(c\) is the number of constraints placed on the table. Note that, \(k\ell\) gives the total number of cells in the contingency table. Moreover, if the test is being run on a frequency distribution rather than a contingency table, we can take \(\ell = 1\).

The number of constraints, \(c\), arise while calculating the expected frequencies based on the underlying hypotheses. The question we are asking ourselves is “how many cell values are pre-determined, based on the assumptions?”. Take, for instance, the simple goodness-of-fit assumptions. In this case we have that \(E_i = np_i\), for \(i=1,\dots,k\). Note, however, that in order to calculate \(E_i\) we are assuming that the total number of observations is going to be \(n\). By assumption, we know that \[E_1 + E_2 + \cdots + E_k = n.\] As a result, once we have determined \(\{E_1, E_2, \dots, E_{k-1}\}\), the final value, \(E_k\) must also be determined as \[E_k = n - E_1 - E_2 - \cdots - E_{k-1}.\] Thus, while we calculate \(k\) expected values, we have a constraint on exactly \(1\) of these values, so \(c=1\). This gives the familiar \(d = k - 1\).

In the contingency table for independence we calculate a total of \(k\ell\) expected values. However, we make the assumption that both \(n_{i,\bullet}\) and \(n_{\bullet,j}\) are fixed for each row and column. This gives \(k + \ell\) constraints, however, it is the case that \[\sum_{i=1}^{k} n_{i,\bullet} = \sum_{j=1}^{\ell} n_{\bullet,j} = n.\] Thus, once we have constrained the \(k\) totals for the rows, and \(\ell - 1\) totals for the columns, the final value for the remaining column has already been constrained as well. Thus, in this case, \(c = k + \ell - 1\). This gives, \[d = k\ell - (k + \ell - 1) = (k - 1)(\ell - 1).\]

An alternative framing for counting the degrees of freedom is to ask ourselves: “how many expected values can we independently compute?”. To answer this we note that we calculate one in each cell, minus any of those that are constrained, hence giving \(d = k\ell - c\). However, in some situations it may be easier to directly count the free to vary expected values. Either way, the assumptions guarantee that the distribution will be approximately chi-squared, and the hypotheses give rise to the number of degrees of freedom.

18.3.3 Performing a Chi-squared Test

In order to perform a chi-squared test we follow a five-step procedure:

  1. Compute the expected cell counts based on the underlying hypothesis.
  2. Compute the \(\chi^2\) test statistic, giving a realization of \(x\).
  3. Determine the null distribution (degrees of freedom).
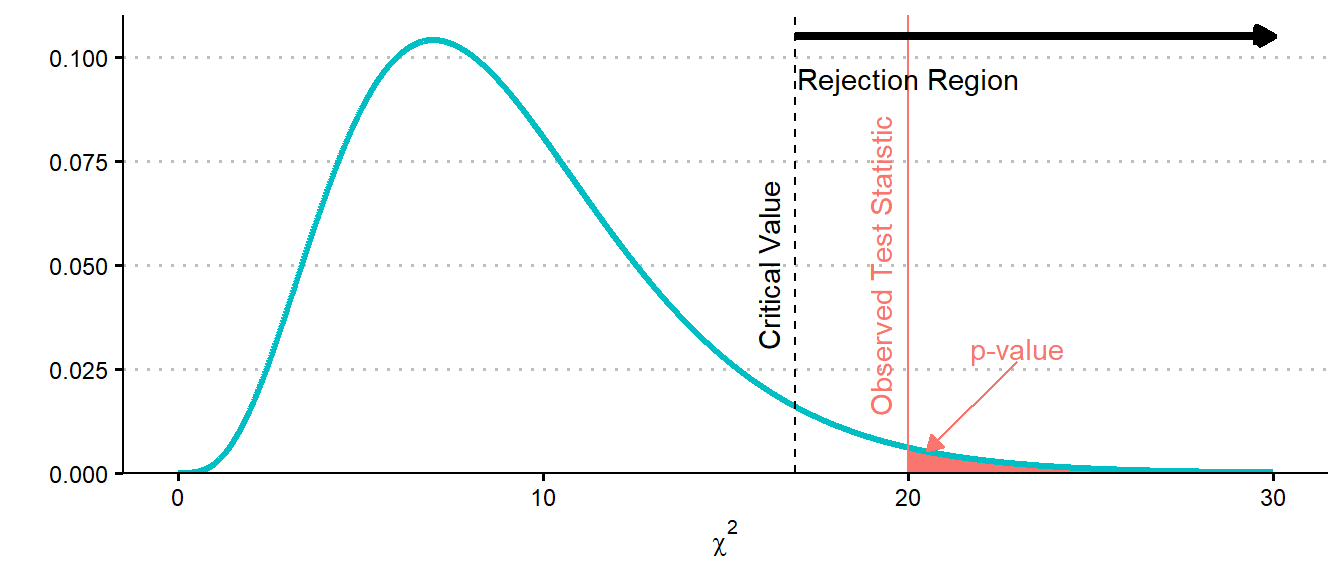
  4. Calculate the \(p\)-value as \(P(\chi^2 > x)\), or determine the relevant (upper-tail) critical value.
  5. Draw and communicate conclusions.

The first three steps are addressed in the previous sections. Once the realization of the test statistic and the null distribution are known, the test proceeds16 either via \(p\)-values or critical values. When attempting to determine the \(p\)-value, it is helpful to consider which tail contradicts the null hypothesis. Under the null hypothesis we should expect that \(O_{i,j} \approx E_{i,j}\), for all \(i\) and \(j\). If this is the case then we have that \(\chi^2\) will be small in magnitude (close to zero). If this is not the case, however, we will see that \(\chi^2\) will be large in magnitude (far from zero), and always positive.17 As a result, it is only the upper tail that we are concerned with in terms of generating \(p\)-values or for finding critical values.

Figure 18.1: The rejection region for a chi-squared hypothesis test. For chi-squared tests we do not differentiate between one- and two-tailed tests. Instead, if the alternative holds, we should expect to see large values of the test statistic. As a result, the \(p\)-value always corresponds to the right-tail probability. The \(p\)-value will, just as in other hypothesis tests, be compared to the level of significance.

Formally, taking \(F\) to represent the cumulative distribution function of a \(\chi^2_d\) random variable, then given \(\chi^2 = x\), the \(p\)-value for the hypothesis test is \(p = 1 - F(x)\). This can be compared to the level of significance, \(\alpha\). Alternatively, the critical value can be determined as \(\chi^2_{d, 1-\alpha}\). Then, if \(x > \chi^2_{d,1-\alpha}\), the null hypothesis is rejected at the \(\alpha\) level of significance. Conclusions are then drawn in the same manner as other hypothesis tests: if the null hypothesis is rejected at the given level of significance, there is sufficient evidence in the data to take the alternative as being a better description of reality than the null. The level of significance is still interpretable as the probability of making a Type I error, and it should still be balanced with the power of the hypothesis test, depending on the contextual requirements.

18.3.4 The Three Common Chi-squared Tests

While it is conceptually possible to test any hypotheses that generate expected frequency distributions, it is most common to test one of the three aforementioned hypotheses: (i) the goodness-of-fit of a distribution, (ii) the homogeneity of two or more populations, or (iii) the independence of two characteristics. Respectively, these tests are often referred to as the chi-squared goodness-of-fit test, the chi-squared test for homogeneity, and the chi-squared test for independence. Each test follows the general framework for a chi-squared test: the expected values are determined, \(\chi^2\) is calculated, the degrees of freedom are determined, and a \(p\)-value is derived. Because of the frequency with which these tests are used, it is useful to summarize each procedure as a concrete example of the relevant hypothesis test.

The Chi-squared Goodness-of-Fit Test

Suppose that observations are made for \(k\) categories, based on a simple random sample, giving \(O_1, \dots, O_k\). In order to test whether these are drawn from a particular distribution or not, we test \[H_0: \text{The Distribution is a Good Fit} \quad H_A: \text{The Distribution Does Not Fit}.\] The expected cell counts, \(E_1, \dots, E_k\) are computed under the null hypothesis (namely, that the distribution fits). In particular, the expected quantities are computed as \[E_i = p_in,\] where \(p_i\) is the probability of observing class \(i\) based on the assumed distribution.

Then, the \(\chi^2\) statistic is computed, \[\chi^2 = \sum_{i=1}^k \frac{(O_i - E_i)^2}{E_i} \stackrel{H_0}{\sim} \chi^2_{k-1}.\]

Finally, supposing that \(\chi^2 = x\), the \(p\)-value is calculated as \(p = P(\chi^2 \geq x)\), where \(\chi^2\) is a \(\chi^2_{k-1}\) random variable.

Because the expected values for testing for independence and homogeneity are equivalent, the test procedures for independence and homogeneity are also equivalent. Recall that the difference between the two test procedures stems from the difference in the data structure18 and in the method of data collection.19 Given that the differences are contextual, the test can be viewed as a single test procedure.

The Chi-squared Test for Homogeneity / Chi-Squared Test for Independence

Suppose that observations are made either from:

  1. A simple random sample from \(k\) distinct populations, producing observations of a trait with \(\ell\) categories; or
  2. A simple random sample from a single population, with two characteristics measured, the first with \(k\) distinct categories and the second with \(\ell\) categories.

In both cases, record the observed data as \(O_{i,j}\) for \(i=1,\dots,k\) (indexing the population or first trait), and \(j=1,\dots,\ell\) (indexing the second trait). In order to test either:

  1. \(H_0: \text{The Populations are Homogenous with Respect to the Trait}\) versus \(H_A: \text{The Populations are Heterogeneous with Respect to the Trait}\); or
  2. \(H_0: \text{The Traits are Independent in the Population}\) versus \(H_A: \text{The Traits are Dependent in the Population}\),

the expected values for each cell can be computed as \[E_{i,j} = \frac{n_{i,\bullet}n_{\bullet,j}}{n}.\]

Then, the \(\chi^2\) statistic is computed, \[\chi^2 = \sum_{i=1}^k\sum_{j=1}^{\ell} \frac{(O_{i,j} - E_{i,j})^2}{E_{i,j}} \stackrel{H_0}{\sim} \chi^2_{(k-1)(\ell-1)}.\]

Finally, supposing that \(\chi^2 = x\), the \(p\)-value is calculated as \(p = P(\chi^2 \geq x)\), where \(\chi^2\) is a \(\chi^2_{(k-1)(\ell-1)}\) random variable.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 18.1

In a batch of flowers that a florist receives the flowers are all either red or white. During this time of the year, they require 3 times as many red flowers as white flowers. They consider a sample of flowers from the shipment to test whether it meets their needs.

Option Observed Frequency
Red Flowers 40
White Flowers 16

Considering testing whether the shipment meets the needs.

  1. What is the expected cell count for ‘White Flowers’?
  2. What is the expected cell count for ‘Red Flowers’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0030580179)

A survey asks respondents to indicate their level of agreement with a statement on a five-point Likert scale: Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. For a particular statement, a researcher wants to know if the responses are uniformly distributed across the five categories.

Option Observed Frequency
Agree 33
Disagree 21
Neutral 14
Strongly Agree 107
Strongly Disagree 37

Considering testing whether the responses are uniformly distributed across the five agreement levels.

  1. What is the expected cell count for ‘Strongly Agree’?
  2. What is the expected cell count for ‘Agree’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0360817529)

A marketing team is testing the effectiveness of four different website designs (A, B, C, and D) in generating clicks. They randomly assign users to see one of the designs and record which design they clicked on. Before the test, they had no reason to believe any design would perform better than another.

Option Observed Frequency
A 75
B 70
C 73
D 73

Considering testing whether the four website designs have the same click-through rate.

  1. What is the expected cell count for ‘C’?
  2. What is the expected cell count for ‘B’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0598691132)

A teacher believes that the grades in their introductory statistics course should follow a certain distribution. There should be an equal number of As and Fs, twice as many Bs and Ds (compared to As), and four times as many Cs (compared to As). At the end of the semester, they want to compare the actual grade distribution of their class to this expected distribution.

Option Observed Frequency
A 25
B 110
C 613
D 170
F 12

Considering testing whether the actual grade distribution of the class matches the teacher’s expected distribution.

  1. What is the expected cell count for ‘D’?
  2. What is the expected cell count for ‘B’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0445842130)

In a batch of flowers that a florist receives the flowers are all either red or white. During this time of the year, they require 3 times as many red flowers as white flowers. They consider a sample of flowers from the shipment to test whether it meets their needs.

Option Observed Frequency
Red Flowers 107
White Flowers 40

Considering testing whether the shipment meets the needs.

  1. What is the expected cell count for ‘White Flowers’?
  2. What is the expected cell count for ‘Red Flowers’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0921784945)

A marketing team is testing the effectiveness of four different website designs (A, B, C, and D) in generating clicks. They randomly assign users to see one of the designs and record which design they clicked on. Before the test, they had no reason to believe any design would perform better than another.

Option Observed Frequency
A 236
B 26
C 18
D 177

Considering testing whether the four website designs have the same click-through rate.

  1. What is the expected cell count for ‘C’?
  2. What is the expected cell count for ‘A’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0148114025)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 101
Green 94
Red 72
Yellow 90

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Blue’?
  2. What is the expected cell count for ‘Green’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0898618802)

A researcher is investigating whether there is a preference for different types of online news sources. They categorize news sources into five types: Traditional Media, Online-Only News, Blogs, Social Media News, and Citizen Journalism. They assume that in the absence of preference, people would access these types equally.

Option Observed Frequency
Blogs 35
Citizen Journalism 95
Online-Only News 33
Social Media News 112
Traditional Media 28

Considering testing whether there is no preference for the different types of online news sources.

  1. What is the expected cell count for ‘Blogs’?
  2. What is the expected cell count for ‘Citizen Journalism’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0893807317)

An individual wishes to consider whether a particular six-sided die is actually fair. They decide to test this, by considering the results of a series of die rolls. They observe the following results.

Option Observed Frequency
1 193
2 31
3 241
4 107
5 119
6 120

Considering testing whether the die is actually fair.

  1. What is the expected cell count for ‘2’?
  2. What is the expected cell count for ‘1’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0371878654)

A survey asks respondents to indicate their level of agreement with a statement on a five-point Likert scale: Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. For a particular statement, a researcher wants to know if the responses are uniformly distributed across the five categories.

Option Observed Frequency
Agree 125
Disagree 203
Neutral 87
Strongly Agree 261
Strongly Disagree 360

Considering testing whether the responses are uniformly distributed across the five agreement levels.

  1. What is the expected cell count for ‘Strongly Disagree’?
  2. What is the expected cell count for ‘Neutral’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0829464018)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 53
Green 69
Red 58
Yellow 85

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Red’?
  2. What is the expected cell count for ‘Yellow’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0087264257)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 81
Green 25
Red 27
Yellow 17

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Red’?
  2. What is the expected cell count for ‘Yellow’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0825558485)

A factory produces items that can have one of three types of defects: Type 1, Type 2, or Type 3. Based on historical data, the expected proportion of these defects is 15%, 35%, and 50% respectively. A quality control inspector takes a sample of recently produced items to check if the current defect distribution matches the historical one.

Option Observed Frequency
Type 1 25
Type 2 30
Type 3 109

Considering testing whether the current defect distribution matches the historical proportions.

  1. What is the expected cell count for ‘Type 3’?
  2. What is the expected cell count for ‘Type 2’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0713607792)

A researcher is investigating whether there is a preference for different types of online news sources. They categorize news sources into five types: Traditional Media, Online-Only News, Blogs, Social Media News, and Citizen Journalism. They assume that in the absence of preference, people would access these types equally.

Option Observed Frequency
Blogs 26
Citizen Journalism 35
Online-Only News 34
Social Media News 26
Traditional Media 30

Considering testing whether there is no preference for the different types of online news sources.

  1. What is the expected cell count for ‘Blogs’?
  2. What is the expected cell count for ‘Citizen Journalism’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0623260475)

A researcher is investigating whether there is a preference for different types of online news sources. They categorize news sources into five types: Traditional Media, Online-Only News, Blogs, Social Media News, and Citizen Journalism. They assume that in the absence of preference, people would access these types equally.

Option Observed Frequency
Blogs 1608
Citizen Journalism 1305
Online-Only News 1843
Social Media News 361
Traditional Media 93

Considering testing whether there is no preference for the different types of online news sources.

  1. What is the expected cell count for ‘Social Media News’?
  2. What is the expected cell count for ‘Online-Only News’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0546896186)

A survey asks respondents to indicate their level of agreement with a statement on a five-point Likert scale: Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. For a particular statement, a researcher wants to know if the responses are uniformly distributed across the five categories.

Option Observed Frequency
Agree 251
Disagree 94
Neutral 232
Strongly Agree 69
Strongly Disagree 136

Considering testing whether the responses are uniformly distributed across the five agreement levels.

  1. What is the expected cell count for ‘Strongly Agree’?
  2. What is the expected cell count for ‘Neutral’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0918783570)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 98
Green 92
Red 95
Yellow 96

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Blue’?
  2. What is the expected cell count for ‘Red’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0614898882)

A factory produces items that can have one of three types of defects: Type 1, Type 2, or Type 3. Based on historical data, the expected proportion of these defects is 15%, 35%, and 50% respectively. A quality control inspector takes a sample of recently produced items to check if the current defect distribution matches the historical one.

Option Observed Frequency
Type 1 87
Type 2 62
Type 3 177

Considering testing whether the current defect distribution matches the historical proportions.

  1. What is the expected cell count for ‘Type 3’?
  2. What is the expected cell count for ‘Type 1’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0769598382)

A researcher is studying the distribution of blood types in a specific population. According to known population statistics, the distribution of blood types A, B, AB, and O should be 45%, 10%, 5%, and 40% respectively. The researcher collects a sample of individuals to see if their blood type distribution matches these expected proportions.

Option Observed Frequency
A 3150
AB 46
B 166
O 2375

Considering testing whether the blood type distribution in the sample matches the known population statistics.

  1. What is the expected cell count for ‘AB’?
  2. What is the expected cell count for ‘O’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0498487302)

In a large city, the mode of transportation used by commuters is thought to be distributed as follows: 60% drive alone, 20% use public transit, 15% carpool, and 5% bike or walk. A transportation planner conducts a survey to see if the current distribution matches these expectations.

Option Observed Frequency
Bike/Walk 42
Carpool 98
Drive Alone 389
Public Transit 125

Considering testing whether the current distribution of commuting modes matches the expected proportions.

  1. What is the expected cell count for ‘Public Transit’?
  2. What is the expected cell count for ‘Carpool’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0251285380)

In a large city, the mode of transportation used by commuters is thought to be distributed as follows: 60% drive alone, 20% use public transit, 15% carpool, and 5% bike or walk. A transportation planner conducts a survey to see if the current distribution matches these expectations.

Option Observed Frequency
Bike/Walk 56
Carpool 175
Drive Alone 614
Public Transit 230

Considering testing whether the current distribution of commuting modes matches the expected proportions.

  1. What is the expected cell count for ‘Drive Alone’?
  2. What is the expected cell count for ‘Carpool’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0557822442)

A researcher is studying the distribution of blood types in a specific population. According to known population statistics, the distribution of blood types A, B, AB, and O should be 45%, 10%, 5%, and 40% respectively. The researcher collects a sample of individuals to see if their blood type distribution matches these expected proportions.

Option Observed Frequency
A 387
AB 40
B 90
O 390

Considering testing whether the blood type distribution in the sample matches the known population statistics.

  1. What is the expected cell count for ‘AB’?
  2. What is the expected cell count for ‘O’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0383738967)

A geneticist is studying the inheritance of a particular trait that is determined by three possible genotypes: AA, Aa, and aa. According to Mendelian genetics, if both parents are heterozygous (Aa), the expected ratio of these genotypes in their offspring is 1:2:1. The geneticist examines a sample of offspring to test this theoretical ratio.

Option Observed Frequency
aa 104
Aa 243
AA 81

Considering testing whether the observed genotype ratio in the offspring follows the Mendelian expectation.

  1. What is the expected cell count for ‘aa’?
  2. What is the expected cell count for ‘Aa’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0856974614)

A survey asks respondents to indicate their level of agreement with a statement on a five-point Likert scale: Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. For a particular statement, a researcher wants to know if the responses are uniformly distributed across the five categories.

Option Observed Frequency
Agree 3915
Disagree 11726
Neutral 106
Strongly Agree 3645
Strongly Disagree 787

Considering testing whether the responses are uniformly distributed across the five agreement levels.

  1. What is the expected cell count for ‘Disagree’?
  2. What is the expected cell count for ‘Neutral’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0375041190)

In a batch of flowers that a florist receives the flowers are all either red or white. During this time of the year, they require 3 times as many red flowers as white flowers. They consider a sample of flowers from the shipment to test whether it meets their needs.

Option Observed Frequency
Red Flowers 246
White Flowers 91

Considering testing whether the shipment meets the needs.

  1. What is the expected cell count for ‘Red Flowers’?
  2. What is the expected cell count for ‘White Flowers’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0951767049)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 13
Green 15
Red 19
Yellow 23

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Yellow’?
  2. What is the expected cell count for ‘Blue’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0877868967)

A teacher believes that the grades in their introductory statistics course should follow a certain distribution. There should be an equal number of As and Fs, twice as many Bs and Ds (compared to As), and four times as many Cs (compared to As). At the end of the semester, they want to compare the actual grade distribution of their class to this expected distribution.

Option Observed Frequency
A 190
B 1128
C 224
D 97
F 102

Considering testing whether the actual grade distribution of the class matches the teacher’s expected distribution.

  1. What is the expected cell count for ‘B’?
  2. What is the expected cell count for ‘F’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0984766254)

A researcher is studying the distribution of blood types in a specific population. According to known population statistics, the distribution of blood types A, B, AB, and O should be 45%, 10%, 5%, and 40% respectively. The researcher collects a sample of individuals to see if their blood type distribution matches these expected proportions.

Option Observed Frequency
A 582
AB 46
B 344
O 833

Considering testing whether the blood type distribution in the sample matches the known population statistics.

  1. What is the expected cell count for ‘O’?
  2. What is the expected cell count for ‘A’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0041376159)

An individual wishes to consider whether a particular six-sided die is actually fair. They decide to test this, by considering the results of a series of die rolls. They observe the following results.

Option Observed Frequency
1 130
2 98
3 39
4 86
5 35
6 105

Considering testing whether the die is actually fair.

  1. What is the expected cell count for ‘6’?
  2. What is the expected cell count for ‘2’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0143176555)

An individual wishes to consider whether a particular six-sided die is actually fair. They decide to test this, by considering the results of a series of die rolls. They observe the following results.

Option Observed Frequency
1 93
2 59
3 92
4 87
5 83
6 83

Considering testing whether the die is actually fair.

  1. What is the expected cell count for ‘4’?
  2. What is the expected cell count for ‘6’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0148468275)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 71
Green 63
Red 54
Yellow 67

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Red’?
  2. What is the expected cell count for ‘Yellow’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0558218419)

A survey asks respondents to indicate their level of agreement with a statement on a five-point Likert scale: Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. For a particular statement, a researcher wants to know if the responses are uniformly distributed across the five categories.

Option Observed Frequency
Agree 18
Disagree 21
Neutral 27
Strongly Agree 20
Strongly Disagree 17

Considering testing whether the responses are uniformly distributed across the five agreement levels.

  1. What is the expected cell count for ‘Disagree’?
  2. What is the expected cell count for ‘Neutral’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0538910395)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 50
Green 55
Red 55
Yellow 68

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Red’?
  2. What is the expected cell count for ‘Green’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0038804888)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 17
Green 14
Red 13
Yellow 14

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Blue’?
  2. What is the expected cell count for ‘Red’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0177018299)

A researcher is investigating whether there is a preference for different types of online news sources. They categorize news sources into five types: Traditional Media, Online-Only News, Blogs, Social Media News, and Citizen Journalism. They assume that in the absence of preference, people would access these types equally.

Option Observed Frequency
Blogs 72
Citizen Journalism 75
Online-Only News 57
Social Media News 63
Traditional Media 72

Considering testing whether there is no preference for the different types of online news sources.

  1. What is the expected cell count for ‘Traditional Media’?
  2. What is the expected cell count for ‘Blogs’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0861478994)

An individual wishes to consider whether a particular six-sided die is actually fair. They decide to test this, by considering the results of a series of die rolls. They observe the following results.

Option Observed Frequency
1 69
2 74
3 66
4 63
5 73
6 67

Considering testing whether the die is actually fair.

  1. What is the expected cell count for ‘6’?
  2. What is the expected cell count for ‘2’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0215654951)

A geneticist is studying the inheritance of a particular trait that is determined by three possible genotypes: AA, Aa, and aa. According to Mendelian genetics, if both parents are heterozygous (Aa), the expected ratio of these genotypes in their offspring is 1:2:1. The geneticist examines a sample of offspring to test this theoretical ratio.

Option Observed Frequency
aa 1214
Aa 103
AA 721

Considering testing whether the observed genotype ratio in the offspring follows the Mendelian expectation.

  1. What is the expected cell count for ‘Aa’?
  2. What is the expected cell count for ‘AA’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0149644196)

A company sells candies in bags with four different colors: red, blue, green, and yellow. They claim that each color is equally likely to be in a bag. A consumer buys several bags and counts the number of candies of each color to test this claim.

Option Observed Frequency
Blue 84
Green 459
Red 452
Yellow 131

Considering testing whether each candy color is equally likely in the bags.

  1. What is the expected cell count for ‘Yellow’?
  2. What is the expected cell count for ‘Red’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0837109977)

In a large city, the mode of transportation used by commuters is thought to be distributed as follows: 60% drive alone, 20% use public transit, 15% carpool, and 5% bike or walk. A transportation planner conducts a survey to see if the current distribution matches these expectations.

Option Observed Frequency
Bike/Walk 53
Carpool 204
Drive Alone 938
Public Transit 80

Considering testing whether the current distribution of commuting modes matches the expected proportions.

  1. What is the expected cell count for ‘Public Transit’?
  2. What is the expected cell count for ‘Drive Alone’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0812416757)

A researcher is studying the distribution of blood types in a specific population. According to known population statistics, the distribution of blood types A, B, AB, and O should be 45%, 10%, 5%, and 40% respectively. The researcher collects a sample of individuals to see if their blood type distribution matches these expected proportions.

Option Observed Frequency
A 451
AB 56
B 59
O 661

Considering testing whether the blood type distribution in the sample matches the known population statistics.

  1. What is the expected cell count for ‘A’?
  2. What is the expected cell count for ‘O’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0761931836)

A marketing team is testing the effectiveness of four different website designs (A, B, C, and D) in generating clicks. They randomly assign users to see one of the designs and record which design they clicked on. Before the test, they had no reason to believe any design would perform better than another.

Option Observed Frequency
A 22
B 25
C 26
D 20

Considering testing whether the four website designs have the same click-through rate.

  1. What is the expected cell count for ‘A’?
  2. What is the expected cell count for ‘C’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0330776717)

In a batch of flowers that a florist receives the flowers are all either red or white. During this time of the year, they require 3 times as many red flowers as white flowers. They consider a sample of flowers from the shipment to test whether it meets their needs.

Option Observed Frequency
Red Flowers 38
White Flowers 12

Considering testing whether the shipment meets the needs.

  1. What is the expected cell count for ‘Red Flowers’?
  2. What is the expected cell count for ‘White Flowers’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0809522478)

A factory produces items that can have one of three types of defects: Type 1, Type 2, or Type 3. Based on historical data, the expected proportion of these defects is 15%, 35%, and 50% respectively. A quality control inspector takes a sample of recently produced items to check if the current defect distribution matches the historical one.

Option Observed Frequency
Type 1 25
Type 2 116
Type 3 319

Considering testing whether the current defect distribution matches the historical proportions.

  1. What is the expected cell count for ‘Type 1’?
  2. What is the expected cell count for ‘Type 2’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0129754839)

A marketing team is testing the effectiveness of four different website designs (A, B, C, and D) in generating clicks. They randomly assign users to see one of the designs and record which design they clicked on. Before the test, they had no reason to believe any design would perform better than another.

Option Observed Frequency
A 83
B 115
C 80
D 47

Considering testing whether the four website designs have the same click-through rate.

  1. What is the expected cell count for ‘D’?
  2. What is the expected cell count for ‘C’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0807758827)

An individual wishes to consider whether a particular six-sided die is actually fair. They decide to test this, by considering the results of a series of die rolls. They observe the following results.

Option Observed Frequency
1 25
2 33
3 28
4 31
5 23
6 37

Considering testing whether the die is actually fair.

  1. What is the expected cell count for ‘3’?
  2. What is the expected cell count for ‘1’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0577887689)

In a batch of flowers that a florist receives the flowers are all either red or white. During this time of the year, they require 3 times as many red flowers as white flowers. They consider a sample of flowers from the shipment to test whether it meets their needs.

Option Observed Frequency
Red Flowers 13
White Flowers 161

Considering testing whether the shipment meets the needs.

  1. What is the expected cell count for ‘White Flowers’?
  2. What is the expected cell count for ‘Red Flowers’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0134137354)

A teacher believes that the grades in their introductory statistics course should follow a certain distribution. There should be an equal number of As and Fs, twice as many Bs and Ds (compared to As), and four times as many Cs (compared to As). At the end of the semester, they want to compare the actual grade distribution of their class to this expected distribution.

Option Observed Frequency
A 77
B 4121
C 351
D 98
F 188

Considering testing whether the actual grade distribution of the class matches the teacher’s expected distribution.

  1. What is the expected cell count for ‘F’?
  2. What is the expected cell count for ‘C’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0573542743)

A marketing team is testing the effectiveness of four different website designs (A, B, C, and D) in generating clicks. They randomly assign users to see one of the designs and record which design they clicked on. Before the test, they had no reason to believe any design would perform better than another.

Option Observed Frequency
A 56
B 41
C 59
D 44

Considering testing whether the four website designs have the same click-through rate.

  1. What is the expected cell count for ‘D’?
  2. What is the expected cell count for ‘A’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0972518407)

A researcher is studying the distribution of blood types in a specific population. According to known population statistics, the distribution of blood types A, B, AB, and O should be 45%, 10%, 5%, and 40% respectively. The researcher collects a sample of individuals to see if their blood type distribution matches these expected proportions.

Option Observed Frequency
A 763
AB 72
B 181
O 678

Considering testing whether the blood type distribution in the sample matches the known population statistics.

  1. What is the expected cell count for ‘O’?
  2. What is the expected cell count for ‘AB’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0602031757)

A teacher believes that the grades in their introductory statistics course should follow a certain distribution. There should be an equal number of As and Fs, twice as many Bs and Ds (compared to As), and four times as many Cs (compared to As). At the end of the semester, they want to compare the actual grade distribution of their class to this expected distribution.

Option Observed Frequency
A 139
B 87
C 187
D 160
F 67

Considering testing whether the actual grade distribution of the class matches the teacher’s expected distribution.

  1. What is the expected cell count for ‘F’?
  2. What is the expected cell count for ‘B’?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0401151619)

Self Assessment 18.2

The distribution of blood types is compared across three different groups from different locations.

A B AB O
Group 1 152 29 520 1468
Group 2 121 28 566 1228
Group 3 201 35 735 1778

Considering testing whether the distribution of blood types is the same across the three groups.

  1. What is the expected cell count for AB within Group 3?
  2. What is the expected cell count for A within Group 1?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0912911109)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 26 211 98
Provider B 95 724 348

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Dissatisfied for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0962072302)

A survey asks people from two different cities about their preferred mode of transportation.

Car Public Transit Bike
City X 63 100 207
City Y 66 82 186

Considering testing whether the distribution of preferred transportation modes is the same in both cities.

  1. What is the expected cell count for Car for inhabitants of City X?
  2. What is the expected cell count for Public Transit for inhabitants of City Y?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0836636802)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 14 157 28
Provider B 50 778 152

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Neutral for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0118644283)

The survival rate of plants under two different watering schedules is recorded.

Survived Did Not Survive
Schedule 1 74 399
Schedule 2 100 639

Considering testing whether the survival rate of plants is the same under both watering schedules.

  1. What is the expected cell count for Did Not Survive under watering Schedule 1?
  2. What is the expected cell count for Survived under watering Schedule 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0794967101)

Researchers want to compare the effectiveness of two different teaching methods. They consider two separate classes, applying each method to one of the classes, and record the results for each of the students.

Pass Fail
Method A 98 498
Method B 65 362

Considering testing whether the teaching methods are equally effective.

  1. What is the expected cell count for Pass for students receiving teaching Method A?
  2. What is the expected cell count for Fail for students receiving teaching Method B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0052169317)

The purchase frequency of three different product categories is analyzed for customers from two different regions.

Category I Category II Category III
Region East 812 84 19674
Region West 657 83 16604

Considering testing whether the purchase frequency distribution across product categories is the same for customers from both regions.

  1. What is the expected cell count for Category III for customers in Region West?
  2. What is the expected cell count for Category II for customers in Region East?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0681791445)

The preference for three different social media platforms is surveyed among students from two different universities.

Platform 1 Platform 2 Platform 3
University A 334 92 98
University B 254 68 80

Considering testing whether the preference for social media platforms is the same among students from both universities.

  1. What is the expected cell count for Platform 2 among students at University B?
  2. What is the expected cell count for Platform 3 among students at University A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0683516473)

The distribution of blood types is compared across three different groups from different locations.

A B AB O
Group 1 502 473 318 88
Group 2 305 274 149 56
Group 3 211 233 197 63

Considering testing whether the distribution of blood types is the same across the three groups.

  1. What is the expected cell count for O within Group 3?
  2. What is the expected cell count for AB within Group 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0923768272)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 155 100
Medication B 67 59

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for Improved for patients receiving Medication A?
  2. What is the expected cell count for No Improvement for patients receiving Medication B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0044355363)

Two different types of fertilizers are used on separate plots of land, and the yield of crops is categorized.

Low Yield High Yield
Fertilizer X 30 14
Fertilizer Y 115 47

Considering testing whether the distribution of crop yield is the same for both fertilizers.

  1. What is the expected cell count for High Yield for crops grown with Fertilizer Y?
  2. What is the expected cell count for Low Yield for crops grown with Fertilizer X?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0724027344)

The distribution of blood types is compared across three different groups from different locations.

A B AB O
Group 1 264 33 247 522
Group 2 660 74 629 1402
Group 3 185 19 151 350

Considering testing whether the distribution of blood types is the same across the three groups.

  1. What is the expected cell count for A within Group 3?
  2. What is the expected cell count for AB within Group 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0330932658)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 69 81 124
Provider B 77 89 170

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Neutral for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0857094851)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 14 102 83
Provider B 16 144 89

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Neutral for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0829726601)

The purchase frequency of three different product categories is analyzed for customers from two different regions.

Category I Category II Category III
Region East 23 131 83
Region West 18 50 40

Considering testing whether the purchase frequency distribution across product categories is the same for customers from both regions.

  1. What is the expected cell count for Category II for customers in Region East?
  2. What is the expected cell count for Category I for customers in Region West?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0025157688)

Four different brands of tires are tested for tread life.

Low Wear Medium Wear High Wear
Brand A 148 254 81
Brand B 86 117 41
Brand C 37 52 19
Brand D 60 131 42

Considering testing whether the tire brands wear at equal rates.

  1. What is the expected cell count for Medium Wear tires from Brand D?
  2. What is the expected cell count for Low Wear tires from Brand C?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0277883339)

The preference for three different social media platforms is surveyed among students from two different universities.

Platform 1 Platform 2 Platform 3
University A 250 121 45
University B 410 155 91

Considering testing whether the preference for social media platforms is the same among students from both universities.

  1. What is the expected cell count for Platform 1 among students at University A?
  2. What is the expected cell count for Platform 2 among students at University B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0403684747)

Two different types of fertilizers are used on separate plots of land, and the yield of crops is categorized.

Low Yield High Yield
Fertilizer X 88 30
Fertilizer Y 112 50

Considering testing whether the distribution of crop yield is the same for both fertilizers.

  1. What is the expected cell count for Low Yield for crops grown with Fertilizer Y?
  2. What is the expected cell count for High Yield for crops grown with Fertilizer X?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0173049645)

Four different brands of tires are tested for tread life.

Low Wear Medium Wear High Wear
Brand A 45 195 137
Brand B 26 102 86
Brand C 86 321 283
Brand D 79 290 253

Considering testing whether the tire brands wear at equal rates.

  1. What is the expected cell count for Low Wear tires from Brand D?
  2. What is the expected cell count for Medium Wear tires from Brand C?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0604102236)

The occurrence of different types of errors is tracked for two different software development teams.

Syntax Error Logic Error Runtime Error
Team Alpha 69 724 475
Team Beta 36 395 251

Considering testing whether the distribution of error types is the same for both software development teams.

  1. What is the expected cell count for Logic Error by Team Alpha?
  2. What is the expected cell count for Syntax Error by Team Beta?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0082272261)

The purchase frequency of three different product categories is analyzed for customers from two different regions.

Category I Category II Category III
Region East 88 1685 62
Region West 31 913 38

Considering testing whether the purchase frequency distribution across product categories is the same for customers from both regions.

  1. What is the expected cell count for Category I for customers in Region West?
  2. What is the expected cell count for Category II for customers in Region East?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0505595511)

The occurrence of different types of errors is tracked for two different software development teams.

Syntax Error Logic Error Runtime Error
Team Alpha 46 1087 1733
Team Beta 67 1402 2221

Considering testing whether the distribution of error types is the same for both software development teams.

  1. What is the expected cell count for Syntax Error by Team Alpha?
  2. What is the expected cell count for Logic Error by Team Beta?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0991134813)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 63 374
Medication B 34 258

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for No Improvement for patients receiving Medication B?
  2. What is the expected cell count for Improved for patients receiving Medication A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0444129865)

Researchers want to compare the effectiveness of two different teaching methods. They consider two separate classes, applying each method to one of the classes, and record the results for each of the students.

Pass Fail
Method A 154 94
Method B 47 31

Considering testing whether the teaching methods are equally effective.

  1. What is the expected cell count for Fail for students receiving teaching Method B?
  2. What is the expected cell count for Pass for students receiving teaching Method A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0842213312)

Three different factories produce the same product. Samples from each factory are inspected for defects.

Defective Non-Defective
Factory A 24 25
Factory B 168 86
Factory C 170 99

Considering testing whether the factories produce defective items at equal rates.

  1. What is the expected cell count for Defective products produced at Factory A?
  2. What is the expected cell count for Non-Defective products produced at Factory C?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0140130593)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 173 95
Medication B 25 10

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for Improved for patients receiving Medication B?
  2. What is the expected cell count for No Improvement for patients receiving Medication A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0861764935)

A survey asks people from two different cities about their preferred mode of transportation.

Car Public Transit Bike
City X 446 485 72
City Y 84 60 10

Considering testing whether the distribution of preferred transportation modes is the same in both cities.

  1. What is the expected cell count for Bike for inhabitants of City Y?
  2. What is the expected cell count for Public Transit for inhabitants of City X?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0638670325)

The purchase frequency of three different product categories is analyzed for customers from two different regions.

Category I Category II Category III
Region East 191 314 53
Region West 125 204 34

Considering testing whether the purchase frequency distribution across product categories is the same for customers from both regions.

  1. What is the expected cell count for Category II for customers in Region West?
  2. What is the expected cell count for Category I for customers in Region East?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0077833037)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 249 57 43
Provider B 171 52 26

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Dissatisfied for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0230906038)

Two different types of fertilizers are used on separate plots of land, and the yield of crops is categorized.

Low Yield High Yield
Fertilizer X 81 35
Fertilizer Y 72 31

Considering testing whether the distribution of crop yield is the same for both fertilizers.

  1. What is the expected cell count for Low Yield for crops grown with Fertilizer Y?
  2. What is the expected cell count for High Yield for crops grown with Fertilizer X?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0981945871)

Three different factories produce the same product. Samples from each factory are inspected for defects.

Defective Non-Defective
Factory A 90 259
Factory B 89 304
Factory C 36 108

Considering testing whether the factories produce defective items at equal rates.

  1. What is the expected cell count for Defective products produced at Factory B?
  2. What is the expected cell count for Non-Defective products produced at Factory C?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0660218142)

Four different brands of tires are tested for tread life.

Low Wear Medium Wear High Wear
Brand A 114 101 154
Brand B 28 28 43
Brand C 107 96 147
Brand D 40 38 62

Considering testing whether the tire brands wear at equal rates.

  1. What is the expected cell count for High Wear tires from Brand A?
  2. What is the expected cell count for Low Wear tires from Brand C?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0603507524)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 100 49
Medication B 184 92

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for No Improvement for patients receiving Medication A?
  2. What is the expected cell count for Improved for patients receiving Medication B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0127919301)

The occurrence of different types of errors is tracked for two different software development teams.

Syntax Error Logic Error Runtime Error
Team Alpha 103 1016 303
Team Beta 52 582 200

Considering testing whether the distribution of error types is the same for both software development teams.

  1. What is the expected cell count for Runtime Error by Team Beta?
  2. What is the expected cell count for Syntax Error by Team Alpha?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0325629592)

A survey asks people from two different cities about their preferred mode of transportation.

Car Public Transit Bike
City X 54 271 144
City Y 73 311 220

Considering testing whether the distribution of preferred transportation modes is the same in both cities.

  1. What is the expected cell count for Car for inhabitants of City Y?
  2. What is the expected cell count for Public Transit for inhabitants of City X?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0934916072)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 60 51
Medication B 100 86

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for Improved for patients receiving Medication A?
  2. What is the expected cell count for No Improvement for patients receiving Medication B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0572672673)

The distribution of customer satisfaction levels is compared for two different service providers.

Satisfied Neutral Dissatisfied
Provider A 7641 95 1434
Provider B 4356 52 795

Considering testing whether the distribution of customer satisfaction levels is the same for both service providers.

  1. What is the expected cell count for Neutral for customers of Provider A?
  2. What is the expected cell count for Satisfied for customers of Provider B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0178897011)

The survival rate of plants under two different watering schedules is recorded.

Survived Did Not Survive
Schedule 1 82 122
Schedule 2 92 104

Considering testing whether the survival rate of plants is the same under both watering schedules.

  1. What is the expected cell count for Did Not Survive under watering Schedule 1?
  2. What is the expected cell count for Survived under watering Schedule 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0017780193)

Three different factories produce the same product. Samples from each factory are inspected for defects.

Defective Non-Defective
Factory A 6 25
Factory B 15 32
Factory C 21 47

Considering testing whether the factories produce defective items at equal rates.

  1. What is the expected cell count for Defective products produced at Factory B?
  2. What is the expected cell count for Non-Defective products produced at Factory A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0061379516)

Four different brands of tires are tested for tread life.

Low Wear Medium Wear High Wear
Brand A 209 94 183
Brand B 64 19 48
Brand C 128 43 124
Brand D 60 19 49

Considering testing whether the tire brands wear at equal rates.

  1. What is the expected cell count for Medium Wear tires from Brand A?
  2. What is the expected cell count for Low Wear tires from Brand B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0196293482)

The occurrence of different types of errors is tracked for two different software development teams.

Syntax Error Logic Error Runtime Error
Team Alpha 36 14 11
Team Beta 171 54 77

Considering testing whether the distribution of error types is the same for both software development teams.

  1. What is the expected cell count for Syntax Error by Team Alpha?
  2. What is the expected cell count for Logic Error by Team Beta?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0994468529)

Researchers want to compare the effectiveness of two different teaching methods. They consider two separate classes, applying each method to one of the classes, and record the results for each of the students.

Pass Fail
Method A 70 183
Method B 81 225

Considering testing whether the teaching methods are equally effective.

  1. What is the expected cell count for Fail for students receiving teaching Method A?
  2. What is the expected cell count for Pass for students receiving teaching Method B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0098885808)

The survival rate of plants under two different watering schedules is recorded.

Survived Did Not Survive
Schedule 1 85 235
Schedule 2 83 212

Considering testing whether the survival rate of plants is the same under both watering schedules.

  1. What is the expected cell count for Did Not Survive under watering Schedule 2?
  2. What is the expected cell count for Survived under watering Schedule 1?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0149993022)

Patients with a specific condition are given one of two different medications, and their improvement status is recorded.

Improved No Improvement
Medication A 192 51
Medication B 164 55

Considering testing whether the proportion of patients showing improvement is the same for both medications.

  1. What is the expected cell count for No Improvement for patients receiving Medication A?
  2. What is the expected cell count for Improved for patients receiving Medication B?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0729901212)

The survival rate of plants under two different watering schedules is recorded.

Survived Did Not Survive
Schedule 1 84 35
Schedule 2 135 47

Considering testing whether the survival rate of plants is the same under both watering schedules.

  1. What is the expected cell count for Survived under watering Schedule 1?
  2. What is the expected cell count for Did Not Survive under watering Schedule 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0351629880)

The occurrence of different types of errors is tracked for two different software development teams.

Syntax Error Logic Error Runtime Error
Team Alpha 35 622 480
Team Beta 75 1230 1063

Considering testing whether the distribution of error types is the same for both software development teams.

  1. What is the expected cell count for Logic Error by Team Beta?
  2. What is the expected cell count for Runtime Error by Team Alpha?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0663025067)

The distribution of blood types is compared across three different groups from different locations.

A B AB O
Group 1 28 176 242 118
Group 2 17 125 162 76
Group 3 80 441 699 362

Considering testing whether the distribution of blood types is the same across the three groups.

  1. What is the expected cell count for A within Group 1?
  2. What is the expected cell count for B within Group 3?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0858251099)

The survival rate of plants under two different watering schedules is recorded.

Survived Did Not Survive
Schedule 1 284 75
Schedule 2 273 78

Considering testing whether the survival rate of plants is the same under both watering schedules.

  1. What is the expected cell count for Did Not Survive under watering Schedule 1?
  2. What is the expected cell count for Survived under watering Schedule 2?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0433198316)

Two different types of fertilizers are used on separate plots of land, and the yield of crops is categorized.

Low Yield High Yield
Fertilizer X 428 80
Fertilizer Y 380 79

Considering testing whether the distribution of crop yield is the same for both fertilizers.

  1. What is the expected cell count for Low Yield for crops grown with Fertilizer X?
  2. What is the expected cell count for High Yield for crops grown with Fertilizer Y?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0783869530)

The preference for three different social media platforms is surveyed among students from two different universities.

Platform 1 Platform 2 Platform 3
University A 86 100 125
University B 41 43 61

Considering testing whether the preference for social media platforms is the same among students from both universities.

  1. What is the expected cell count for Platform 2 among students at University B?
  2. What is the expected cell count for Platform 3 among students at University A?
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0531325802)

Self Assessment 18.3

A group of kindergarten students are given a survey where they are asked their favourite primary colour, and their favourite season.

Spring Summer Fall Winter
Red 59777 1782 74916 6134
Blue 5231 151 6394 539
Yellow 1370 37 1669 135

Considering testing whether there is any association between a student’s favourite colour and their favourite season.

  1. What is the expected cell count for Blue / Fall
  2. What is the expected cell count for Red / Summer
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0059099673)

Researchers investigate if there’s a connection between a student’s participation in extracurricular activities and their academic performance.

Good Grades Poor Grades
Participates 45 47
Does Not Participate 48 64

Considering testing whether participation in extracurricular activities is independent of academic performance.

  1. What is the expected cell count for Participates / Good Grades
  2. What is the expected cell count for Does Not Participate / Poor Grades
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0387097624)

The relationship between the type of pet owned and the owner’s lifestyle (active vs. sedentary) is studied.

Active Sedentary
Dog 4966 6339
Cat 36 60
Other 3338 4329

Considering testing whether the type of pet owned is associated with the owner’s lifestyle.

  1. What is the expected cell count for Dog / Sedentary
  2. What is the expected cell count for Other / Active
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0972092029)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 107 2663
Print Ad 54 1246

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Online Ad / No Purchase
  2. What is the expected cell count for Print Ad / Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0756846524)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 18 34
Television News 15 25
Print News 13 35

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Online News / High Trust
  2. What is the expected cell count for Print News / Low Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0073226216)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 441 18
Bachelor’s 502 19
Graduate 484 11

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for Graduate / Employed
  2. What is the expected cell count for Bachelor’s / Unemployed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0348838829)

Researchers investigate if there’s a connection between a student’s participation in extracurricular activities and their academic performance.

Good Grades Poor Grades
Participates 63 19
Does Not Participate 45 21

Considering testing whether participation in extracurricular activities is independent of academic performance.

  1. What is the expected cell count for Participates / Good Grades
  2. What is the expected cell count for Does Not Participate / Poor Grades
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0546445364)

Data on the hair colour and eye colour of individuals from a particular population are collected.

Blue Green Brown
Blonde 8 59 2
Brown 5 64 7
Red 6 63 5
Black 6 72 4

Considering testing whether eye colour and hair colour are associated with one another.

  1. What is the expected cell count for Brown / Green
  2. What is the expected cell count for Blonde / Blue
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0324223046)

The connection between a person’s marital status and their level of happiness is examined.

Happy Not Happy
Single 29 25
Married 17 20
Divorced 15 21

Considering testing whether there is an association between marital status and level of happiness.

  1. What is the expected cell count for Married / Happy
  2. What is the expected cell count for Single / Not Happy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0324611316)

Researchers investigate if there’s a connection between a student’s participation in extracurricular activities and their academic performance.

Good Grades Poor Grades
Participates 333 99
Does Not Participate 716 220

Considering testing whether participation in extracurricular activities is independent of academic performance.

  1. What is the expected cell count for Participates / Poor Grades
  2. What is the expected cell count for Does Not Participate / Good Grades
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0676444964)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 22 199
Print Ad 24 176

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Online Ad / Purchase
  2. What is the expected cell count for Print Ad / No Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0025887913)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 20 18
Bachelor’s 10 21
Graduate 24 25

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for Bachelor’s / Employed
  2. What is the expected cell count for High School / Unemployed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0337030086)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 388 189
White 319 161
Black 157 99
Other 236 121

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Black / Accident
  2. What is the expected cell count for Other / No Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0003879471)

The relationship between the type of pet owned and the owner’s lifestyle (active vs. sedentary) is studied.

Active Sedentary
Dog 15 116
Cat 12 97
Other 15 107

Considering testing whether the type of pet owned is associated with the owner’s lifestyle.

  1. What is the expected cell count for Other / Active
  2. What is the expected cell count for Cat / Sedentary
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0057172585)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 36 25
Print Ad 36 19

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Online Ad / Purchase
  2. What is the expected cell count for Print Ad / No Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0901431047)

A study looks at the association between the time of day a person prefers to exercise and their self-reported energy levels.

High Energy Low Energy
Morning 12 15
Afternoon 11 13
Evening 5 8

Considering testing whether preferred exercise time and energy levels are independent.

  1. What is the expected cell count for Morning / Low Energy
  2. What is the expected cell count for Evening / High Energy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0103079578)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 28 53
Television News 25 64
Print News 29 42

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Television News / Low Trust
  2. What is the expected cell count for Print News / High Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0318779016)

The connection between a person’s marital status and their level of happiness is examined.

Happy Not Happy
Single 17 5
Married 13 6
Divorced 19 9

Considering testing whether there is an association between marital status and level of happiness.

  1. What is the expected cell count for Single / Not Happy
  2. What is the expected cell count for Married / Happy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0311211283)

The relationship between the type of pet owned and the owner’s lifestyle (active vs. sedentary) is studied.

Active Sedentary
Dog 648 5
Cat 644 8
Other 656 4

Considering testing whether the type of pet owned is associated with the owner’s lifestyle.

  1. What is the expected cell count for Other / Sedentary
  2. What is the expected cell count for Cat / Active
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0602754099)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 102 21
Bachelor’s 106 40
Graduate 100 30

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for High School / Unemployed
  2. What is the expected cell count for Bachelor’s / Employed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0855182324)

A group of kindergarten students are given a survey where they are asked their favourite primary colour, and their favourite season.

Spring Summer Fall Winter
Red 236 122 172 24
Blue 220 133 203 26
Yellow 243 121 200 18

Considering testing whether there is any association between a student’s favourite colour and their favourite season.

  1. What is the expected cell count for Blue / Summer
  2. What is the expected cell count for Yellow / Fall
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0263454449)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 19 11
Television News 946 594
Print News 856 493

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Print News / Low Trust
  2. What is the expected cell count for Television News / High Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0943215311)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 7 16
White 14 7
Black 7 13
Other 12 12

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Other / Accident
  2. What is the expected cell count for White / No Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0683024444)

A study looks at the association between the time of day a person prefers to exercise and their self-reported energy levels.

High Energy Low Energy
Morning 25 167
Afternoon 266 1814
Evening 99 697

Considering testing whether preferred exercise time and energy levels are independent.

  1. What is the expected cell count for Morning / High Energy
  2. What is the expected cell count for Evening / Low Energy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0569422815)

Data on the hair colour and eye colour of individuals from a particular population are collected.

Blue Green Brown
Blonde 11112 6971 504
Brown 55978 34080 2495
Red 1853 1144 86
Black 34346 21132 1603

Considering testing whether eye colour and hair colour are associated with one another.

  1. What is the expected cell count for Red / Brown
  2. What is the expected cell count for Blonde / Green
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0118148268)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 980 111
White 664 63
Black 3969 447
Other 1948 222

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Other / No Accident
  2. What is the expected cell count for White / Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0192456230)

A study looks at the association between the time of day a person prefers to exercise and their self-reported energy levels.

High Energy Low Energy
Morning 85 156
Afternoon 463 1058
Evening 338 711

Considering testing whether preferred exercise time and energy levels are independent.

  1. What is the expected cell count for Morning / Low Energy
  2. What is the expected cell count for Evening / High Energy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0449099555)

Researchers investigate if there’s a connection between a student’s participation in extracurricular activities and their academic performance.

Good Grades Poor Grades
Participates 38 22
Does Not Participate 25 23

Considering testing whether participation in extracurricular activities is independent of academic performance.

  1. What is the expected cell count for Participates / Good Grades
  2. What is the expected cell count for Does Not Participate / Poor Grades
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0614371455)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 23 5346
Print Ad 16 6798

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Print Ad / No Purchase
  2. What is the expected cell count for Online Ad / Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0298366511)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 95 10596
White 896 100418
Black 2968 331810
Other 165 21935

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Black / No Accident
  2. What is the expected cell count for Red / Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0216617743)

The connection between a person’s marital status and their level of happiness is examined.

Happy Not Happy
Single 75 15
Married 77 27
Divorced 95 17

Considering testing whether there is an association between marital status and level of happiness.

  1. What is the expected cell count for Divorced / Happy
  2. What is the expected cell count for Married / Not Happy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0990805174)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 12 206
Television News 8 189
Print News 16 216

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Online News / Low Trust
  2. What is the expected cell count for Television News / High Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0867549393)

A group of kindergarten students are given a survey where they are asked their favourite primary colour, and their favourite season.

Spring Summer Fall Winter
Red 127 38 48 72
Blue 112 31 62 66
Yellow 129 35 68 87

Considering testing whether there is any association between a student’s favourite colour and their favourite season.

  1. What is the expected cell count for Red / Spring
  2. What is the expected cell count for Blue / Winter
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0286898475)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 20 8
Print Ad 20 14

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Print Ad / Purchase
  2. What is the expected cell count for Online Ad / No Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0311902844)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 33 35
Television News 40 44
Print News 37 32

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Print News / Low Trust
  2. What is the expected cell count for Television News / High Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0203809642)

Data on the hair colour and eye colour of individuals from a particular population are collected.

Blue Green Brown
Blonde 35 27 105
Brown 188 95 524
Red 25 16 71
Black 39 19 103

Considering testing whether eye colour and hair colour are associated with one another.

  1. What is the expected cell count for Red / Green
  2. What is the expected cell count for Black / Blue
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0550908343)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 25 64
Bachelor’s 23 55
Graduate 38 43

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for Bachelor’s / Unemployed
  2. What is the expected cell count for High School / Employed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0884192537)

Data on the hair colour and eye colour of individuals from a particular population are collected.

Blue Green Brown
Blonde 298 1486 2304
Brown 142 731 1239
Red 74 394 644
Black 756 3515 6091

Considering testing whether eye colour and hair colour are associated with one another.

  1. What is the expected cell count for Blonde / Green
  2. What is the expected cell count for Black / Blue
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.02\) level of significance?

(Question ID: 0745326372)

Data on the hair colour and eye colour of individuals from a particular population are collected.

Blue Green Brown
Blonde 337 2177 305
Brown 117 726 96
Red 57 435 70
Black 1029 6946 983

Considering testing whether eye colour and hair colour are associated with one another.

  1. What is the expected cell count for Black / Brown
  2. What is the expected cell count for Blonde / Blue
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0280695196)

A group of kindergarten students are given a survey where they are asked their favourite primary colour, and their favourite season.

Spring Summer Fall Winter
Red 77 15 210 81
Blue 58 18 199 81
Yellow 53 17 202 108

Considering testing whether there is any association between a student’s favourite colour and their favourite season.

  1. What is the expected cell count for Red / Winter
  2. What is the expected cell count for Yellow / Summer
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.03\) level of significance?

(Question ID: 0048780043)

A group of kindergarten students are given a survey where they are asked their favourite primary colour, and their favourite season.

Spring Summer Fall Winter
Red 45 51 1431 58
Blue 119 163 3753 124
Yellow 36 43 1082 50

Considering testing whether there is any association between a student’s favourite colour and their favourite season.

  1. What is the expected cell count for Red / Fall
  2. What is the expected cell count for Blue / Spring
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.01\) level of significance?

(Question ID: 0787842794)

The connection between a person’s marital status and their level of happiness is examined.

Happy Not Happy
Single 4793 7812
Married 14771 24233
Divorced 27 48

Considering testing whether there is an association between marital status and level of happiness.

  1. What is the expected cell count for Married / Not Happy
  2. What is the expected cell count for Divorced / Happy
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.08\) level of significance?

(Question ID: 0666601665)

A marketing team wants to know if there’s a link between the type of advertisement shown and whether a customer makes a purchase.

Purchase No Purchase
Online Ad 32 210
Print Ad 21 247

Considering testing whether the type of advertisement is independent of whether a customer makes a purchase.

  1. What is the expected cell count for Print Ad / Purchase
  2. What is the expected cell count for Online Ad / No Purchase
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.06\) level of significance?

(Question ID: 0791377467)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 25 29
Bachelor’s 15 28
Graduate 28 39

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for Bachelor’s / Unemployed
  2. What is the expected cell count for High School / Employed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0359078611)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 427 552
White 32 42
Black 223 292
Other 958 1458

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Red / Accident
  2. What is the expected cell count for Black / No Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0461157674)

Researchers investigate if there’s a connection between a student’s participation in extracurricular activities and their academic performance.

Good Grades Poor Grades
Participates 869 108
Does Not Participate 3215 353

Considering testing whether participation in extracurricular activities is independent of academic performance.

  1. What is the expected cell count for Participates / Poor Grades
  2. What is the expected cell count for Does Not Participate / Good Grades
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.05\) level of significance?

(Question ID: 0078797251)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 23807 1133
Bachelor’s 6338 280
Graduate 623 31

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for Graduate / Employed
  2. What is the expected cell count for Bachelor’s / Unemployed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.1\) level of significance?

(Question ID: 0786922460)

A survey asks individuals about their primary source of news and their level of trust in the media.

High Trust Low Trust
Online News 417 323
Television News 446 355
Print News 71 56

Considering testing whether the primary source of news is independent of the level of trust in the media.

  1. What is the expected cell count for Online News / High Trust
  2. What is the expected cell count for Print News / Low Trust
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.09\) level of significance?

(Question ID: 0701255820)

A car manufacturer investigates if there is a relationship between the color of a car and the likelihood of it being involved in an accident.

Accident No Accident
Red 6469 974
White 2069 350
Black 970 162
Other 467 85

Considering testing whether the color of a car is independent of its likelihood of being involved in an accident.

  1. What is the expected cell count for Black / No Accident
  2. What is the expected cell count for Red / Accident
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.04\) level of significance?

(Question ID: 0293156727)

A study examines the relationship between educational attainment and employment status in a city.

Employed Unemployed
High School 33 6127
Bachelor’s 32 6033
Graduate 33 5933

Considering testing whether there is an association between a person’s level of education and their employment status.

  1. What is the expected cell count for High School / Employed
  2. What is the expected cell count for Bachelor’s / Unemployed
  3. What is the value of the test statistic for testing the null hypothesis?
  4. What is the \(p\)-value for testing the null hypothesis?
  5. What is the conclusion, to test at an \(\alpha = 0.07\) level of significance?

(Question ID: 0807600870)

  1. There is no way, for instance, to consider the average favourite colour for a group of school-aged children, or to consider the median political party that a region supports. There may be techniques that can measure related quantities numerically, however, these are not typically numerical quantities.↩︎

  2. For instance, do children report red and blue as being their favourite colour with equal proportions?↩︎

  3. For instance, is a child’s favourite colour related to their favourite animal, or are these two characteristics independent?↩︎

  4. Such as the Poisson, generating counts.↩︎

  5. While this is described as being a distribution that is explicitly characterized, rather than deriving from a named distribution, the underlying distribution is in fact named. Notably, the distribution follows a multinomial distribution, where the multinomial extends the concept of the binomial to multiple different options. This is characterized by a total number of observations (\(60\) in the example), as well as a set of probabilities of observing each class (\(p_1,\dots,p_6\)).↩︎

  6. Such as one’s career.↩︎

  7. Say, defined by individuals’ gender.↩︎

  8. The notation of a subscript \(\bullet\) is used to suggest that you sum over that index. So, \(n_{i,\bullet} = \sum_{j} n_{i,j}\).↩︎

  9. Notice that, if this were actually true, then for two populations, say \(i\) and \(k\), we would have \[\dfrac{n_{i,j}}{n_{i,\bullet}} = \frac{n_{\bullet,j}}{n} = \frac{n_{k,j}}{n_{k,\bullet}},\] exactly as desired.↩︎

  10. For instance, we may take a random sample of individuals and ask them for their gender and their job.↩︎

  11. If the random variables are continuous, the same breakdown applies with density functions rather than probability mass functions, giving \(f_{X,Y}(x,y) = f_X(x)f_Y(y)\).↩︎

  12. The reason for this stems from the fact that each population may be different sizes. If you have one population that is much larger than another, in the overall simple random sample, you should expect far more realizations from this population. In the separate population framing, this would only hold if you choose to select fewer individuals from the smaller populations. The difference is analogous to the difference between simple random sampling and stratified random sampling.↩︎

  13. Or, equivalently, a contingency table↩︎

  14. As with all rules of thumb, this is a rough rule that indicates where these tests may be appropriate. Some sources may indicate that you should have above \(10\) for some expected values. Others indicate that, if you have many cells under consideration, it suffices to have \(80\%\) of the expected cells above \(5\), so long as none are zero. As with all size requirements, the truth depends on the underlying reality, however, the larger the expected counts, the better the approximation will work.↩︎

  15. There are two important points on this. First, under a true simple random sample, independence will typically be a reasonable assumption. Second, the required independence is distinct from the type of independence we may test for using the chi-squared test. Independence of observations means that two subsequent realizations should not ever depend on one another. The independence that we may test for, conversely, refers to independence of traits within a population (that is, traits on the same individual are independent of one another).↩︎

  16. As do all other tests in the NHST framework.↩︎

  17. This arises since the differences between the observed and expected values are squared, so any difference, positive or negative, becomes a positive contribution to the test statistic.↩︎

  18. Testing for homogeneity involves multiple separate populations, whereas testing for independence involves a single population with multiple traits.↩︎

  19. Testing for homogeneity relies on multiple simple random samples from various populations, whereas, testing for independence relies on a single simple random sample.↩︎