13 Methods of Estimation

13.1 The Role of Estimation, Estimators, and Estimates

When introducing sample statistics, we had been discussing their role as relating to population parameters. That is, to formalize the process we are following we started from the position that there is a population that we wish to learn about, and specifically some parameter(s) in that population whose value we would like to know. Owing to the fundamental limitations we are faced with¹ we are unable to directly observe the population in full. As a result, the parameter value remains unknown to us. Instead, we attempt to understand the population by observing a sample. We are able to consider the distribution of this sample via the data distribution, and we are able to compute statistics on this sample. These statistics, intuitively, are connected to the parameter values of interest.² The sampling distribution of the sample statistics provides one technique for codifying the connection between the parameter value and the value of the statistic that we can compute.

In this process it is possible to view statistics as serving two distinct, but related, roles. The first is as a means of describing the true sample. That is, we use statistics in the description of the data distribution, and they provide a description of what we actually observed. The second is as a “guess” as to the value of an unknown parameter. The process of using data to “guess” the value of an unknown parameter is referred to as estimation, and it is one of the primary goals of statistical inference.

Definition 13.1 (Estimation) Any procedure that attempts to infer the value of a parameter in a population using information from a sample is referred to as estimation. With estimation, statistics are computed from data with the explicit goal of providing information about the population.

Thus, if we are interested in the mean value for some trait in a population, we take a sample, and using this sample compute the sample mean for this value, then we can view this as a procedure to estimate to true mean in the population. This process of estimation will not, generally, give us an exact value for the population parameter, however, if we follow efficient estimation procedures, we can be fairly confident that the reported values will be close to the truth.

We will formalize the process of estimation by considering an arbitrary parameter in the population. Suppose that this parameter has an unknown value, denoted $\theta$.³ Owing to limitations in our ability to directly observe the population, we cannot directly compute $\theta$. Instead, it is our goal to determine an estimated value for $\theta$ using data that are observed in a sample. Before we have collected any data at all, we can determine a procedure that we could follow to generate these estimated values. This procedure is referred to as an estimator.

Definition 13.2 (Estimator) An estimator is a mathematical procedure (function) that takes in observable data (from a sample) and outputs an estimate for a parameter value. Estimators are specific to the parameter that they are attempting to estimate. For instance, if $\theta$ is an unknown parameter of interest, then we may define \[\widehat{\theta}(X_1,X_2,\dots,X_n) = \widehat{\theta},\] as a procedure that takes in a sample ($X_1, \dots, X_n$) and outputs a value. In this framework we hope that, once computed, $\widehat{\theta} \approx \theta$.

Estimators are simply statistics that are computed with the goal of approximating the value of a parameter. Thus, any of the statistics that we have seen previously can be viewed as estimators. The sample mean, \[\overline{X} = \widehat{\mu} = \frac{1}{n}\sum_{i=1}^n X_i,\] can be viewed as an estimator of the population mean, $\mu$. The sample variance, \[S^2 = \widehat{\sigma}^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2,\] can be viewed as an estimator of the population variance, $\sigma^2$. The defining feature of an estimator is that it is a mathematical function, meaning that it takes in data that may be observed in a sample. An estimator is not a specific numeric value. Because estimators take as input data from a sample, and because we regard the data from samples as being random, estimators are random variables. For instance, the value of the sample mean can be regarded as a random value prior to a sample being observed.

The fact that estimators are random variables means that estimators have distributions. Estimators are, however, just statistics. In Chapter 12 we defined the sampling distribution of a statistic. The sampling distribution of a statistic was the distribution of a statistic when it was regarded as a process that takes in random data, and outputs a value. The sampling distribution emerges by considering the repeated sampling of data and the computation of a statistic using these data. Estimators have sampling distributions in exactly the same way. That is, we may consider repeatedly drawing samples from a population of interest. On each of these samples we may apply our estimator to generate a guess as the parameter value. If we repeated this over many samples, we would observe many values computed by the estimator. These values would differ owing to sampling variability. The distribution that emerges from this repeated process is the sampling distribution of an estimator.

Example 13.1 (Charles’ Excitement for the Hockey Season) As the summer came to a close, Charles began to get very excited about the upcoming hockey season. This time of year is always exciting as teams begin to make roster announcements, and Charles is excitedly scrolling through the list of players currently under contract. When hockey is being played there are typically 6 individuals on the ice at any point for each team, the goalie and 5 skaters. Charles recognizes that this group of 6 players is not a perfectly random sample, but decides to consider it as such in any event. If the 6 players were regarded as a random sample, Charles recognizes that the average weight of the players on the ice at any time could be viewed as an estimator of the average weight of players on the team as a whole.

Curious as to how such an estimator would behave, Charles records the following data, comprising the weight of every player (in pounds) currently on the roster.

224	216	178	190	175	217	217	188	192	187
181	183	170	184	202	166	181	215	179	199
196	217	192	178	230	212	209	188	202	193
201	158	220	196	209	238	202	196	240	205
225	222	207

Because this represents the entire population, Charles is able to know that the true average weight for players on this team is 199.5348837 pounds.

Describe the sampling distribution of the estimator outlined by Charles.
Describe how different realizations from the sampling distribution could be generated. Generate several of these values, explaining the procedure.
(Challenge) construct a histogram that represents the probability mass function for the sampling distribution of the estimator.

Solution

The sampling distribution can be constructed by conceiving of every sample of size $6$ from this population as being equally likely. There are $\dbinom{43}{6}$ different combinations of $6$ players that can be selected here, and each of these combinations is thought of as being equally likely. Then, with each combination, the sample mean \[\overline{x} = \frac{1}{6}(x_1 + x_2 + x_3 + x_4 + x_5 + x_6),\] can be computed. This value will be assigned probability \[\frac{1}{\binom{43}{6}}.\] Now, it is important to note that there are multiple combinations that will result in the same $\overline{x}$, and as a result, when summarizing the probabilities some combinations will have higher probability than others. Still, the sampling distribution of the estimator can be conceived of as being the equally likely probability model applied to the sample of $6096454$ possible combinations of players.
A realization of the sampling distribution is generated by selecting $6$ individuals at random and computing their average weight. For instance, if we number the players from left-to-right, top-to-bottom, $1$ through $43$, then perhaps we select 2, 17, 14, 35, 37, 43 as a sample. These individuals have weights 216, 181, 184, 209, 202, 207, resulting in a sample average of 199.8333333. Note that this is reasonably close to the population mean, but not exactly equal. We can consider doing this several times over.
- A sample of 41, 35, 40, 16, 20, 22 produces weights of 225, 209, 205, 166, 199, 217 with a mean of 203.5.
- A sample of 22, 23, 9, 42, 40, 34 produces weights of 217, 192, 192, 222, 205, 196 with a mean of 204.
- A sample of 8, 26, 11, 4, 41, 34 produces weights of 188, 212, 181, 190, 225, 196 with a mean of 198.6666667.
- A sample of 29, 4, 42, 35, 6, 3 produces weights of 202, 190, 222, 209, 217, 178 with a mean of 203.
Because there are over 6 million possible combinations, it is infeasible to consider this by-hand. Instead, we can use R, for instance, to construct all possible combinations of the sample weights, and plot these together.

The sampling distribution for the sample mean, with samples of 6 players.

While the value of an estimator is random when the estimator is thought of as a mathematical procedure, once we have data, we are able to compute an exact value using the estimator. The value that the sample mean will take on, before we have observed a sample, is unknown and random. However, once we have taken a sample, the value of the sample mean is some fixed number. These fixed values that are computed using estimators are referred to as estimates. We will typically regard estimates as “guesses” of the value of a parameter.

Definition 13.3 (Estimate) A constant value that is computed using an estimator is referred to as an estimate. An estimate is derived by applying some estimator, $\widehat{\theta}$, to an observed sample of data, $X_1=x_1, X_2=x_2,\dots, X_n=x_n$. Once computed, the value of the estimate is regarded as a proxy for the value of the parameter, $\theta$.

Because estimates are constant values, computed for a specific sample, estimates are not random. There is no distribution for estimates. Instead, they are simply numeric values that are tied to the specific sample from which they were computed. Thus, in the population there are parameters, which take on some unknown, constant value. These are not random, however, they are also unobservable. In an attempt to infer the value of a parameter, we can devise a mathematical procedure used for estimation. This procedure, referred to as an estimator, is a random function since it takes in data from an unobserved sample. The distribution of the estimator is the sampling distribution. Once a sample is actually drawn, the estimator can be applied to the sample, producing an estimate. The estimate is a fixed numeric value, and as such is not random. Unlike the parameter value, the value of the estimate is known since it is derived from a sample. The goal of estimation is to have the value of the estimate be a reasonable approximation for the value of the parameter.

Example 13.2 (Charles and the Starting Line) Still invested in the upcoming hockey season, Charles decides to continue investigating the weights of the players. Instead of considering the full roster, Charles begins to consider the population as simply the members of the team who will likely be on the ice to start the first game of the season, excluding the goalie. Taking these $5$ individuals as the populations, the relevant weights are: $175$, $212$, $230$, $196$, and $201$. Suppose that these are considered the population, and Charles considers estimating values about this population through the use of samples.

Write down the complete sampling distribution for the sample mean if samples of size $2$ are taken.
Write down an estimate for the population mean if a sample of size $3$ is taken. What estimator did you use?
Suppose that instead of considering the average, Charles is interested in the minimum weight of the players. What estimator can be used to estimate this value from samples of size $4$? Identify the corresponding sampling distribution.
Describe, in relation to this current setup, the difference between the sampling distribution and the population distribution.

Solution

There are a total of $\dbinom{5}{2} = 10$ possible samples that can be taken. These result in:
- $175$, $212$ for a mean of $193.5$
- $175$, $230$ for a mean of $202.5$
- $175$, $196$ for a mean of $185.5$
- $175$, $201$ for a mean of $188$
- $212$, $230$ for a mean of $221$
- $212$, $196$ for a mean of $204$
- $212$, $201$ for a mean of $206.5$
- $230$, $196$ for a mean of $213$
- $230$, $201$ for a mean of $215.5$
- $196$, $201$ for a mean of $198.5$
There are no repeated values here and so the sampling distribution is an equally likely probability model with the set of possible outcomes equalling \[\mathcal{X} = \{193.5, 202.5, 182.5, 188, 221, 204, 206.5, 213, 215.5, 198.5\}.\] Specifically, each outcome has probability $0.1$.
Suppose that the sample we obtained was $175, 196, 230$. Then, if we used the sample mean as the estimator, we would estimate the value of the population mean to be \[\frac{601}{3} = 200.333333.\]
We could consider using the sample minimum as the estimator. In this case, with samples of size $4$ there are $5$ possible samples (one where each observation is held out). In every sample where $175$ is included, it will be the minimum. In the sample where it is not included, the minimum will be $196$. Thus, suppose that we take $X_{(1)}$ to be the sample minimum estimator, then \[p_{X_{(1)}}(x) = \begin{cases} \frac{4}{5} & x = 175 \\ \frac{1}{5} & x = 196 \\ 0 & \text{otherwise} \end{cases}.\]
Here, the five measurements of weight correspond to the population. If we sample from these five individuals, then any statistics that are computed using this sample will be an estimate of the relevant value in the population. These samples, containing just a subset of the five weights, are subject to sampling variability based on which individual observations are included or are not included. As a result, if we envision the set of possible samples that could be realized we can discuss the distribution of the statistics via the sampling distribution. These distributions answer the question “if we were to repeatedly sample from this population, what is the probability we will observe particular values for the computed estimate?” For instance, in (c) we saw that if we take samples of size $4$ from the population, there is a $0.8$ probability that the estimated minimum will exactly equal the population minimum. This $0.8$ comes from the sampling distribution of the sample minimum.

The process described above is more specifically referred to as point estimation. In point estimation, we form point estimators and generate the corresponding point estimates to approximate the value of a parameter using one, single value. That is, a point estimator outputs a single number that should be our “best guess” to the value of the parameter. Point estimation stands in contrast to interval estimation where instead of making a guess of a single value, we give a range of plausible values that the parameter may take on. Typically, if something is referred to as an “estimator” or an “estimate”, it is implied that this is in reference to a “point estimator” or a “point estimate”. We will investigate interval estimation in the coming chapters.

13.2 Assessing the Performance of Estimators

The process of estimation described above is a seemingly intuitive method for approximating parameter values through the use of sample statistics. However, to this point we have not stopped to consider whether this intuitive procedure actually works well in practice. To remedy this, we need to devise techniques that will allow us to assess the performance of estimators broadly. We want to be sure that, if we are using an estimate as an approximation for a parameter, we can be reasonably certain that this is a justifiable thing to do. While defining the performance of an estimator requires some care, intuitively, an estimator will have better performance if it typically produces estimates that are close to the truth.

13.2.1 The Bias of an Estimator

One way to formalize the performance of an estimator is to suggest that we want estimates to be close to the truth, on average. Intuitively, an estimator that is reliable is one that, were it to be computed over and over again, would have a typical value that is close to the parameter. Now, because estimators are random functions and they have distributions, it is also possible to conceive of the expected value of an estimator. If an estimator is reliable it is reasonable to suggest that the expected value of the estimator should be close to the parameter. As a result, we can define a measure of performance based on how far the estimator is from the truth, on average. We call this the bias of an estimator.

Definition 13.4 (Bias (of an estimator)) The bias of an estimator, $\widehat{\theta}$, of a parameter $\theta$ is a measure of the expected difference between the estimator and the truth. That is, \[\text{Bias}(\widehat{\theta}) = E[\widehat{\theta} - \theta] = E[\widehat{\theta}] - \theta.\]

All else equal, it is preferable to have estimators that have a low bias. If the bias is low then on average we expect the estimator to be close to the truth. A low bias provides a reasonable justification for using an estimator in many situations. In the event that the bias of an estimator is shown to be $0$, we call the estimator unbiased.

Definition 13.5 (Unbiased Estimator) An unbiased estimator is any estimator, $\widehat{\theta}$, with a bias of $0$. That is, \[E[\widehat{\theta}] - \theta = 0 \implies E[\widehat{\theta}] = \theta.\]

If an estimator is unbiased then its expectation exactly coincides with the truth. If you were able to take many different samples, compute estimates on each of those samples, and then take the average of those various estimates, an unbiased estimator will have this average coincide with the true parameter value. This is typically a desirable trait, and it is very common to try to find unbiased estimators for parameters of interest. Many of the common estimators that we have seen are unbiased. Despite the utility of unbiased estimators, knowing that something is unbiased is not enough to justify its use. Moreover, it is often possible to find many different unbiased estimators for the same parameter, which nevertheless give different estimates. In these cases it is important to be able to choose between different estimators on the basis of additional performance metrics.

Example 13.3 (Sadie and Charles Explore Bias) Fascinated by having the bias to assess the quality of estimators, Charles and Sadie turn their attention to trying to determine as many ways of estimating population means as they can think of. For each of the following pairs of estimators, assess the bias of each of them and determine which estimator is preferable based on the bias alone.

Charles considers an arbitrary population and suggests that both $\overline{X}$, the sample mean, and $X_1$, the first observation, may be used to estimate the mean of the distribution.
Sadie, thinking of a Poisson distribution, suggests that both the sample variance, $S^2$, and $\dfrac{1}{2}(X_1 - X_2)^2$ may work to estimate $\lambda$.
In a normal population, Charles and Sadie both want to estimate $\mu^2$. Charles suggests taking the average of $X_i^2$, that is \[\frac{1}{n}\sum_{i=1}^n X_i^2,\] while Sadie suggests taking $\overline{X}^2$.

Solution

Both of these estimators are unbiased for the truth. To see this note that \[E[\overline{X}] = E\left[\frac{1}{n}\sum_{i=1}^n X_i\right] = \frac{1}{n}\sum_{i=1}^n E[X_i] = \mu.\] Similarly, we know that $E[X_i] = \mu$ for all $i = 1,\dots, n$ so $E[X_1] = \mu$. As a result, the biases of both estimators are the same and selecting either is equivalent in terms of the bias.
Recall that for a Poisson distribution, $E[X] = \text{var}(X) = \lambda$. Thus, \[\begin{align*} E[S^2] &= E\left[\frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n E[(X_i - \lambda + \lambda - \overline{X})^2] \\ &= \frac{1}{n-1}\sum_{i=1}^n E[(X_i - \lambda)^2] + 2E[(X_i - \lambda)(\lambda - \overline{X})] + E[(\lambda - \overline{X})^2] \\ &= \frac{1}{n-1}\sum_{i=1}^n \text{var}(X_i) - 2E[(X_i - \lambda)(\overline{X} - \lambda)] + \text{var}(\overline{X}) \\ &= \frac{1}{n-1}\sum_{i=1}^n \left[\lambda - \frac{2}{n}\sum_{j=1}^n E[(X_i-\lambda)(X_j-\lambda)] + \frac{\lambda}{n}\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n \left[\lambda - \frac{2}{n}E[(X_i-\lambda)^2] + \frac{\lambda}{n}\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n \lambda - \frac{\lambda}{n} \\ &= \lambda. \end{align*}\] On the other hand, we have that \[\begin{align*} E\left[\frac{1}{2}(X_1 - X_2)^2\right] &= \frac{1}{2}\left(E[X_1^2] - 2E[X_1X_2] + E[X_2^2]\right)\\ &= \frac{1}{2}\left((\lambda + \lambda^2) - 2E[X_1]E[X_2] + (\lambda + \lambda^2)\right) \\ &= \lambda. \end{align*}\] As a result, both of the proposed estimators are unbiased and just as in the previous case, they cannot be selected between one another based on bias alone.
First, consider the expected value of Charles’ estimator. Notably, \[\begin{align*} E\left[\frac{1}{n}\sum_{i=1}^nX_i^2\right] &= \frac{1}{n}\sum_{i=1}^n E[X_i^2] \\ &= \frac{1}{n}\sum_{i=1}^n (\sigma^2 + \mu^2) \\ &= \sigma^2 + \mu^2. \end{align*}\] Meanwhile, for Sadie’s estimator we find \[\begin{align*} E\left[\overline{X}^2\right] &= \text{var}(\overline{X}) + E[\overline{X}]^2 \\ &= \frac{\sigma^2}{n} + \mu^2. \end{align*}\] As a result, both estimators are biased. The one proposed by Charles has a bias of \[\sigma^2 + \mu^2 - \mu^2 = \sigma^2,\] while Sadie’s has a bias of \[\frac{\sigma^2}{n} + \mu^2 - \mu^2 = \frac{\sigma^2}{n}.\] As a result, Sadie’s estimator has a smaller bias and is preferable in that regard.

In a normal population, Charles and Sadie both want to estimate $\mu^2$. Charles suggests taking the average of $X_i^2$, that is \[\frac{1}{n}\sum_{i=1}^n X_i^2,\] while Sadie suggests taking $\overline{X}^2$.

A Note on Variance Estimation

The standard technique for computing the sample variance is to take \[\widehat{\sigma}^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2.\] This is a slightly strange formula for the sample variance where it would feel far more natural for \[\widehat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})^2.\] However, the reason that the first technique is typically used is that it is an unbiased estimator, where the more natural version is biased. To see this consider \[\begin{align*} E[\widehat{\sigma}^2] &= E\left[\frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})^2\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n E[(X_i - \mu + \mu - \overline{X})^2] \\ &= \frac{1}{n-1}\sum_{i=1}^n E[(X_i - \mu)^2] + 2E[(X_i - \mu)(\mu - \overline{X})] + E[(\mu - \overline{X})^2] \\ &= \frac{1}{n-1}\sum_{i=1}^n \text{var}(X_i) - 2E[(X_i - \mu)(\overline{X} - \mu)] + \text{var}(\overline{X}) \\ &= \frac{1}{n-1}\sum_{i=1}^n \left[\sigma^2 - \frac{2}{n}\sum_{j=1}^n E[(X_i-\mu)(X_j-\mu)] + \frac{\sigma^2}{n}\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n \left[\sigma^2 - \frac{2}{n}E[(X_i-\mu)^2] + \frac{\sigma^2}{n}\right] \\ &= \frac{1}{n-1}\sum_{i=1}^n \sigma^2 - \frac{\sigma^2}{n} \\ &= \sigma^2. \end{align*}\] Note that in this derivation, the first step simply adds $0$ (by adding and subtracting $\mu$). Moreover, when trying to find $E[(X_i - \mu)(X_j - \mu)]$ we use the fact that if $i\neq j$ then $X_i \perp X_j$ and so \[E[(X_i - \mu)(X_j - \mu)] = E[(X_i - \mu)]E[(X_j - \mu)],\] which is zero. Thus, dividing by $n-1$ gives an unbiased estimator for $\sigma^2$.

Note that this means that if we instead divided by $n$ we would find that the bias were \[\frac{n-1}{n}\sigma^2 - \sigma^2 = \frac{-\sigma^2}{n}.\] As $n$ increases this bias tends towards $0$ and the difference between the two estimators is minimal.

When we summarized random variables with location summaries we saw that the variability inherent in the random variable was missed. We can think of bias as being a measure of the estimator’s location, relative to the truth. In this sense the variability of the estimator is also overlooked when reporting bias. We may consider two estimators, each of which is unbiased for the truth. In terms of their average location, there is no difference between the two of them. However, it may be the case that one of the estimators is far more variable than the other. If this is so then we know that, while on average it will equal the true value, we will also expect it to be further from the truth on any given realization. That is, a good estimator is one that is close to the truth on average, but that also is not too variable. If the estimator moves around a lot, it is less reliable, and any given estimate from the estimator may be likely to be quite far from the truth. Thus, just as with random variables we needed to include measures of location and variability, so too with estimators should include measures of the bias and variance.

13.2.2 The Variance of an Estimator

Remembering that estimators are random variables and are realizations from a sampling distribution, we are able to discuss the variance of an estimator in exactly the same way as we would discuss the variance of any random quantity.

Definition 13.6 (Variance of an Estimator) The variance of an estimator is the variance of the sampling distribution of the estimator. That is, an estimator $\widehat{\theta}$, will have variance given by \[\text{var}(\widehat{\theta}) = E[(\widehat{\theta} - E[\widehat{\theta}])^2] = E[\widehat{\theta}^2] - E[\widehat{\theta}]^2.\] If an estimator is unbiased then $E[\widehat{\theta}] = \theta$ and the variance simplifies to \[\text{var}(\widehat{\theta}) = E[\widehat{\theta}^2] - \theta^2.\]

The variance of an estimator can be interpreted in much the same way as the variance of any random variable is. Specifically, variance is a measure of the spread around an estimator’s mean. If the process of drawing samples and computing estimates were to be repeated over and over again, then a higher variance estimator will have more spread in the estimates that are computed as compared to a lower variance estimator. In this sense, the variance of an estimator serves as a measure of the reliability of the estimator. It is typically preferable, all else equal, to have an estimator with low variability. This gives more confidence that any estimate that is computed is likely to be near any other estimate that could have been computed, with less susceptibility to the specifics of the random sample.⁴

Example 13.4 (Sadie and Charles Moved Beyond Bias) Content in their exploration of bias alone, Sadie and Charles realize that they must be missing part of the picture. In particular, they found two estimators that have equivalent bias but, intuitively, they each know that they are not equivalent estimators. They want to understand why that is. Together, they set out to investigate the two estimators that Charles was considering for the population mean of an arbitrary distribution.

In an arbitrary population, is $\overline{X}$, the sample mean, or $X_1$, the first observation, a better estimator for the mean of the distribution? Why?
Suppose that an estimator is considered of the form \[\widehat{\theta} = \sum_{i=1}^n \omega_iX_i,\] where $\sum_{i=1}^n \omega_i = 1$. Then the sample mean takes $\omega_i = \dfrac{1}{n}$ for all $i$, and the first point takes $\omega_1 = 1$ and $\omega_i = 0$ for all other points. How does this general estimator compare to the sample mean?

Solution

The sample mean is a better estimator than the first observation. The bias is the same for each estimator, and so we can directly compare the variance. The variance of $\overline{X}$ is \[\text{var}(\overline{X}) = \frac{\sigma^2}{n}.\] On the other hand, the first data point, $X_1$, will have variance $\sigma^2$. As a result, the variance for the single estimator is $n$ times larger than the variance of the sample mean, justifying its use instead.
First, we consider the bias. Note that \[\begin{align*} E[\widehat{\theta}] = E\left[\sum_{i=1}^n \omega_iX_i\right] \\ &= \sum_{i=1}^n \omega_iE[X_i] \\ &= \sum_{i=1}^n \omega_i\mu \\ &= \mu\sum_{i=1}^n \omega_i = \mu. \end{align*}\] Thus, the estimator is unbiased. Then, to consider the variance of the estimator we get \[\begin{align*} \text{var}(\widehat{\theta}) &= \text{var}\left(\sum_{i=1}^n \omega_iX_i\right) \\ &= \sum_{i=1}^n \text{var}(\omega_iX_i) \\ &= \sum_{i=1}^n \omega_i^2\text{var}(X_i) \\ &= \sigma^2\sum_{i=1}^n \omega_i^2. \end{align*}\] Then, the variance of the estimator depends on $\sum_{i=1}^n \omega_i^2$.⁵

In many cases the variance of an estimator becomes a secondary consideration once the bias is known to be small. If you have shown a comparatively small bias for two estimators then by reducing the variance of the estimator you are increasing the probability that the estimates produced will be near the truth. This becomes especially relevant when the estimators under consideration are unbiased. When comparing two unbiased estimators, the natural point of comparison is in the variance. We know that on average both estimators will produce estimates of the truth. To have a more useful estimator for a single sample, however, we want the one that will more reliably produce values that are close to the truth, which is to say, the lower variance estimator. In fact, if we consider only unbiased estimators, then it would be most ideal to search for the unbiased estimator with the lowest possible variance, the so-called minimum variance unbiased estimator.

Definition 13.7 (Minimum Variance Unbiased Estimator (MVUE)) The minimum variance unbiased estimator (MVUE) is the unbiased estimator for a parameter that has the smallest possible variance among all unbiased estimators for that parameter. That is, if $\widehat{\theta}^*$ is the MVUE, and $\widehat{\theta}$ is any estimator such that $E[\widehat{\theta}] = \theta$, then \[\text{var}(\widehat{\theta}^*) \leq \text{var}(\widehat{\theta}).\]

Generally, the MVUE will depend on both the underlying population distribution and on the parameter that is being estimated. It is also often the case that MVUEs are not feasible to find. However, in cases where they are known and easy to calculate, there is a strong justification for their application. Specifically, the MVUE is guaranteed to be the lowest variance estimator among any estimator that will be correct on average. Some commonly applied estimators happen to be the MVUEs. For instance, if the data are normally distributed then $\overline{X}$ is the MVUE for $\mu$. Moreover, if the data are from a binomial distribution, then $\widehat{p}$, the sample proportion, is the MVUE for $p$. In general, however, the sample mean will not be the MVUE for the population mean, nor will the sample variance be the MVUE for the population variance. Despite this, the sample mean and variance remain useful estimators for their respective parameters. Why is this the case?

The MVUE codifies one possible condition for the optimality of an estimator. That is, if we define the optimal estimator to be unbiased and with low variance, then the MVUE is optimal. However, this is a rather restrictive definition for optimality. Specifically, requiring estimators to be unbiased removes many useful estimators that wind-up performing better on average. Often it will be possible to sacrifice a little in terms of the bias for major gains in terms of the variance. Doing this may be worthwhile, undermining the optimality of the MVUE. What’s more, the MVUE only considers the properties of bias and variance in performance assessment. While the bias and variance are the most commonly applied metrics for estimator performance, other considerations are often useful, depending on the context.

13.2.3 The Mean Squared Error, Accuracy, and Precision

The MVUE achieves a fairly restrictive trade-off between the bias and variance of the estimator. Specifically, by only considering estimators that are unbiased, the MVUE begins from a restrictive place. As was previously argued, it is important to consider both the mean and the variance when assessing the performance of an estimator, though, that does not specifically necessitate considering unbiased estimators. Instead, we may wish to consider estimators that are biased, but only if there is a sufficient reduction in variance to justify this. In essence, we are hoping to find estimators that minimize both quantities simultaneously. As it turns out, this is well-summarized through the use of the mean squared error.

Definition 13.8 (Mean Squared Error) The mean squared error (MSE) of an estimator is the expected square distance between the estimator and the true value of the parameter. If $\widehat{\theta}$ is an estimator for $\theta$, then \[\text{MSE}(\widehat{\theta}) = E[(\widehat{\theta} - \theta)^2].\]

Estimators with lower MSE values are typically preferred, all else equal. The MSE of an estimator at first glance appears to be similar to the variance. However, where in the variance the squared distance is computed to the expected value of the estimator, $E[\widehat{\theta}]$, for the MSE the squared distance is computed to the true value of the estimator, $\theta$. Note that for unbiased estimators we know that $E[\widehat{\theta}] = \theta$, and so if the bias of an estimator is $0$, then the MSE is exactly equal to the variance. However, even when the bias of the estimator is non-zero, the MSE still balances the bias and the variance of the estimator. This is best seen through the bias-variance decomposition.

The Bias-Variance Decomposition

The mean squared error of an estimator can be decomposed such that \[\text{MSE}(\widehat{\theta}) = \text{Bias}(\widehat{\theta})^2 + \text{var}(\widehat{\theta}).\] In this way, reducing the MSE is akin to the simultaneous reduction of the bias and the variance, allowing a trade-off between them.

The decomposition of the MSE into the bias and variance formalizes the notion that we wish to simultaneously minimize each quantity. It also directly allows us to consider the tradeoff between bias and variance that is inherent in much of statistics. Often, by reducing the variance of an estimator you must incur extra bias, or by reducing the bias, you must incur extra variance. The MSE provides a metric to understand when these tradeoffs are worthwhile and when they are not. In a sense, finding minimal MSE estimators is a generalization of the procedure of finding the MVUE. In this case, however, we are permitted to consider estimators which have positive bias (so long as their reduced variance justifies consideration).

Example 13.5 (Charles and Sadie Consider Variance Estimators) When introduced originally, Charles was quite perturbed by the sample variance formula and the division by $n-1$. In a conversation with Sadie, Charles expressed some frustration that the formula should just divide by $n$. What’s the big difference between the two, after all? Sadie, remembering this conversation, returns to Charles and points out that at least they now understand that the $n-1$ exists to make the estimator unbiased. Charles was satisfied until learning of the MSE and bias-variance decomposition. “Why not sacrifice some bias in exchange for a more interpretable formula? What is really being lost?” Sadie points out that they could answer this by considering the MSE of the estimators. Charles thinks that is a great idea and recalls reading somewhere that, in a normal population, the variance of $S^2$ is $\dfrac{2\sigma^4}{n-1}$.

What is the MSE of $S^2$?
What is the MSE of the variance estimator that divides by $n$ in place of $n-1$?
Frustrated by the arbitrariness, Charles declares, “Why not divide by $n+1$ instead?” If this were done, what would the MSE be?
Which of the three estimators is quantitatively the best?

Solution

Note that given that $E[S^2] = \sigma^2$, the bias of the estimator is $0$. As a result, \[\text{MSE}(S^2) = \text{var}(S^2) = \frac{2}{n-1}\sigma^4.\]
To find the MSE we consider first the bias. We know that the estimator can be written as $\dfrac{n-1}{n}S^2$ and so \[E\left[\frac{n-1}{n}S^2\right] = \frac{n-1}{n}E[S^2] = \frac{n-1}{n}\sigma^2.\] Thus, the bias is given by \[\frac{n-1}{n}\sigma^2 - \sigma^2 = \frac{-\sigma^2}{n}.\] We can perform a similar calculation for the variance, giving \[\text{var}\left(\frac{n-1}{n}S^2\right) = \frac{(n-1)^2}{n^2}\text{var}(S^2) = 2\frac{(n-1)}{n^2}\sigma^4.\] Then we get that \[\text{MSE}(S_{n}^2) = \left(-\frac{\sigma^2}{n}\right)^2 + 2\frac{(n-1)}{n^2}\sigma^4 = \frac{2n - 1}{n^2}\sigma^4.\]
We can use a similar procedure here. Note that \[S_{n+1}^2 = \frac{n-1}{n+1}S^2\] and so for the bias we get \[\left(\frac{n-1}{n+1} - 1\right)\sigma^2 = \frac{-2\sigma^2}{n+1}.\] Then, working on the variance we find \[\text{var}(S_{n+1}^2) = 2\frac{(n-1)}{(n+1)^2}\sigma^4.\] Thus, combined the MSE is given by \[\text{MSE}(S_{n+1}^2) = \frac{2n + 2}{(n+1)^2}\sigma^4 = \frac{2}{n+1}\sigma^4.\]
We can compare the three different MSEs either algebraically, graphically, or via example. The following graph plots their respective values for $n=2$ through to $n=30$. Note that if $n=1$ then all estimators will produce $0$ so it is not a valid point of comparison. Also note that this is simply graphing the constant multiple of $\sigma^4$. This can be interpreted as either a case where $\sigma^2 = 1$ or else as the multiple of the squared variance that is relevant.

Note that the lowest MSE is the estimator dividing by $n+1$, followed by that dividing by $n$, followed by the standard variance estimator. Algebraically it is clear to see that $\text{MSE}(S^2) \geq \text{MSE}(S_{n+1}^2)$, since dividing by $n+1$ will be smaller for all $n$. While it is slightly more involved, it is possible to show that dividing by $n$ will always fall between these two. That is, quantitatively, the best estimator (of those considered) for the variance of a normal population is the sample variance that divides by $n+1$ rather than by $n-1$.

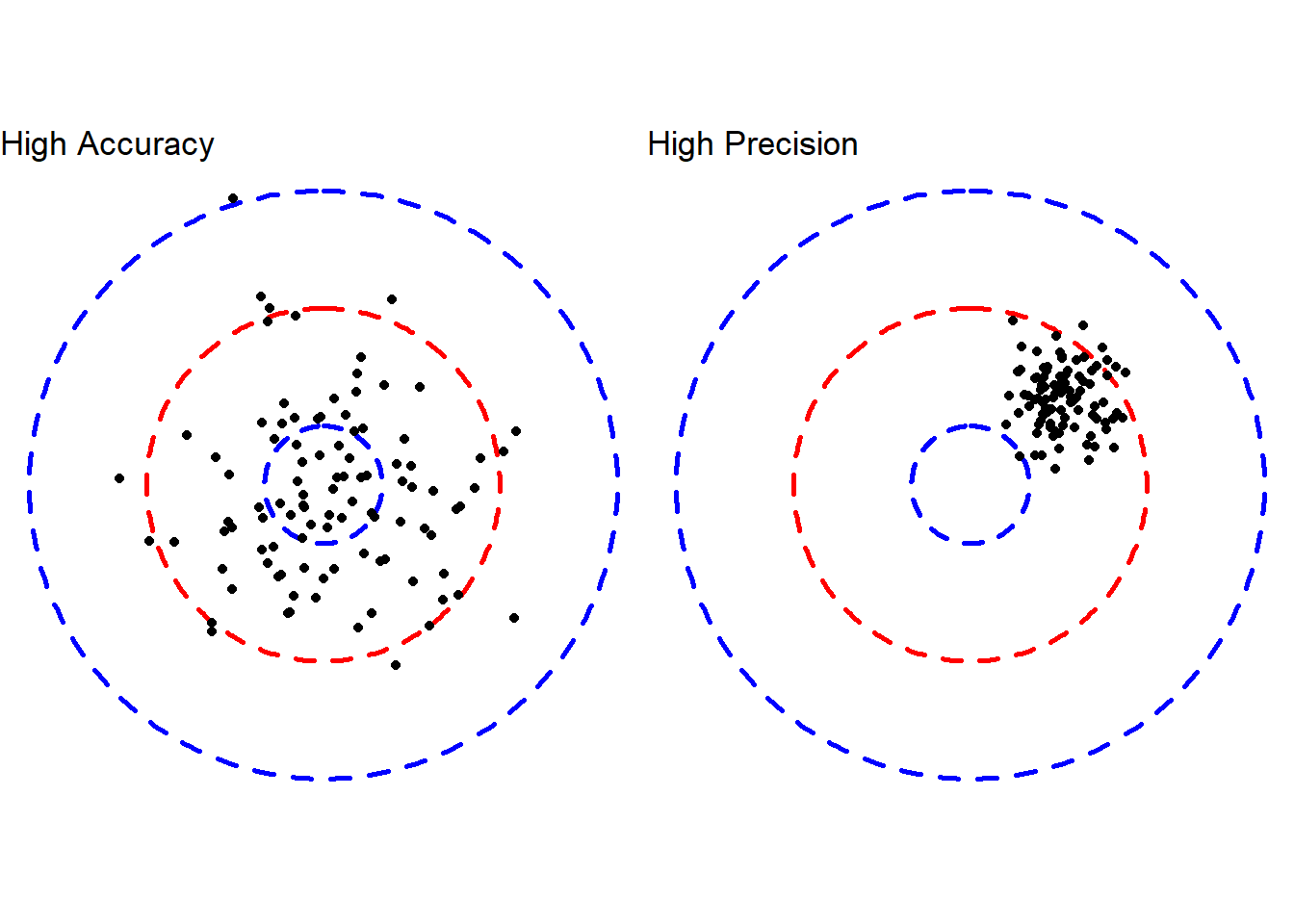
The innate tradeoff between the bias and variance of estimators is understandable through its analogue in accuracy and precision. When speaking of the bias of an estimator we are speaking primarily of the accuracy of the estimator. To say that the bias is low is to say that, on average, we expect the estimated values to center on the truth. On average, a low bias estimator will be nearly correct. This says nothing to how tightly the points concentrate around the truth. In contrast, the variance of the estimator is a measure of the precision of the estimator. A low variance estimator will frequently take values that are clustered around one another. This cluster may or may not be near the true value, however, there will be minimal spread in them. A perfect estimator would have high accuracy (low bias) and high precision (low variance), however, it will often be the case that we can achieve on aim or the other. Using the MSE allows us to quantitatively consider the tradeoffs between accuracy and precision, and find an estimator that strikes a good balance.

Figure 13.1: A plot demonstrating the difference between high accuracy (with low precision) and high precision (with low accuracy). Higher accuracy refers to the tendency to be centered correctly on the truth. High precision refers for the tendency to be tightly clustered together. The accuracy is analogous to the bias of an estimator where the precision is analogous to the variance of an estimator. The mean squared error combines both concepts.

In general, unless otherwise specified, the best estimator to use in a given situation will be the estimator with the lowest MSE. There may be scenarios where an unbiased estimator is particularly important, in which case, you may instead search for the MVUE. Alternatively, there may be scenarios where the precision is of utmost importance, seeking the lowest variance estimator among those that are reasonable. Still, more often than not, the minimal MSE estimator will be preferred from a performance perspective. With that said, there are occasionally considerations beyond the bias or variance of an estimator that ought to be considered when assessing performance.

13.2.4 Conditions Beyond the Mean Squared Error

While it is typically the case that our primary concern is the MSE of an estimator, there are other considerations that we may need to make on occasion. It is important to always consider that we are assessing estimators for a particular purpose in a particular setting. The generality of the MSE rule makes it a useful place to start, however, we should always be cognizant of the particular demands of our scenario. For instance, the bias, variance, and MSE of an estimator are all dependent on the sampling distribution of the estimator. The sampling distribution, in turn, will often depend on the population distribution. As a result, estimators that minimize the MSE will typically only minimize the MSE for a specific population distribution. If the estimator is applied to data drawn from a different population, the MSE will typically change. As a result, if we are uncertain about the population distribution we may prefer to find an estimator that will perform well regardless of what the truth happens to be, even if it has a higher MSE for certain populations than other estimators. This is a measure of the robustness of an estimator.

Definition 13.9 (Robust (Estimator)) Roughly speaking, an estimator is said to be robust if the estimator performs well even when the distributional assumptions made regarding the estimators are incorrect.

Robustness is a property which, when present, gives more certainty that the estimators will perform well in practice. There are also practical considerations we may need to make regarding estimators. For instance, we may be concerned with how well we are able to compute estimates using the estimators. If an estimator is theoretically performant, but in practice, it requires substantial computational resources to calculate, then it may not be practical in use. Additionally, there may be assumptions beyond the distributional assumptions addressed with robustness required for certain estimators. It may be preferable to select an estimator with fewer assumptions, or perhaps, less restrictive assumptions, even if that means sacrificing quantitative performance. One final consideration that may be required is the popularity of the estimator. In certain fields there are expected analytical pathways since the individuals working or researching in those fields are used to interpreting particular estimators. In these cases, even if a more performant estimator exists, the added utility of estimating quantities that others know and understand, and the capacity to compare to work that was previously done, may be a benefit worthy of consideration.

Example 13.6 (Understanding the Sample Variance Estimator) Charles and Sadie continue to discuss the sample variance estimator. After determining (Example 13.5) that the MSE of the estimator that divides by $n+1$ has a better MSE than the estimator that divides by $n-1$, Charles is perturbed that it has become so common to take the sample variance to be defined as the unbiased estimator. When discussing with Sadie, Charles notes that unbiasedness is only one small part of an estimator’s performance, and that it is an arbitrary decision to select it. Sadie, sensing the frustration that Charles feels at the scenario, suggests that they do an exercise together of making an argument in favour of each of the three estimators that they have been studying, $S^2$, $S_{n}^2$, and, $S_{n+1}^2$.

What may the arguments include?

Solution

For $S^2$, the primary argument quantitatively is that it is unbiased. Moreover, for even moderate $n$, the reduction in the MSE that the other estimators achieve over $S^2$ will be minimal, and as such, the unbiasedness is a desirable property. Further, when sample variances are computed and reported, it is most common that they will be computed and reported according to $S^2$. As a result, it is important for interpretability and communication to estimate variance in the same manner when discussing results with other people.

For $S_n^2$, the primary argument is that it is conceptually straightforward. It mirrors the sample mean, and feels far less arbitrary than either $S^2$ or $S_{n+1}^2$. While the estimator is biased, for moderate $n$ the bias will be fairly small, and despite the bias, the MSE is an improvement over the MSE of $S^2$. As a result, you can gain simplicity of the estimator, improve the performance in terms of MSE, and only minimally sacrifice on the bias.

For $S_{n+1}^2$, the primary argument is that it is the best estimator by the standards of the MSE. When considering accuracy and precision jointly, it will perform better than either $S^2$ or $S_n^2$. What is more, the bias that the estimator has is minimal for even moderate $n$. The added complexity of the formula feels no more complex, and no more arbitrary, than the complexity in the formula for taking $n-1$, and this complexity could be justified by appealing to the optimality of the estimator.

There are undoubtedly considerations beyond those listed here that may be worth considering. The overarching point is that, ultimately, estimators are meant to be tools that provide useful information in particular settings. It is important to keep the context of the estimation problem in mind when selecting an estimator, rather than simply deferring to a rigid quantitative principle.

13.3 Procedures for Estimation

In most situations considered until this point, the parameter of interest in the population has been a quantity with a well-defined sample analog. For instance, we were concerned with the population mean, $\mu$, and as such it made sense to consider the sample mean, $\overline{X}$, as an estimator. This is a reasonable approach for parameters that map well onto descriptive statistics, however, many distributions will be characterized by parameters that do not have well-studied sample variants. Despite this, there will still often be a need to derive estimators for these parameters. As a result, it is desirable to have strategies that can be applied in order to derive estimators for parameters of interest in general. We refer to such strategies as estimation procedures.

There are two particularly prominent estimation procedures, which together, cover many of the most common estimators in frequent use. These are maximum likelihood estimators and method of moment estimators. In maximum likelihood estimation, the goal is to determine the parameter value that, if it were the correct value, would result in the highest likelihood of observing the sample that is observed. These estimators are in frequent use and have many desirable theoretical properties. Calculating the maximum likelihood estimator relies on differential calculus, as it necessitates us solving optimization problems.⁶ Method of moments estimators, on the other hand, take the intuitive idea of matching sample and population statistics directly, and generalize this to account for arbitrary parameters to be estimated. As a result, the method of moments procedure is quite intuitive, and provides an accessible introduction to general estimation techniques.

13.4 Method of Moments Estimators

Fundamentally, method of moments estimators are derived by finding estimators that match population moments to sample moments. To understand this fully, we start by defining moments.

Definition 13.10 ((Population) Moments) The $k$th population moment of a random variable $X$ is defined to be $$m_K = E[X^k]$. Thus, the expected value is the first population moment, $E[X^2]$ is the second, and so forth. In general, if the population distribution is characterized by a parameter $\theta$, then the population moments will be functions of the unknown parameter $\theta$.

The population moments can, in a sense, be thought of as containing most of the information in the distribution. As a result, two distributions that share the same set moments can, in many situations, be thought of as the same distribution. Thus, if an estimator of $\theta$ reproduces the population moments then this estimator can be regarded as a useful estimator, at least in theory. As a result, in method of moments estimation, we match population moments to sample moments.

Definition 13.11 (Sample Moments) The $k$th sample moment of a random sample, $X_1,\dots,X_n$, is given by the sample average of $X_i^k$. That is, \[\widehat{m}_k = \frac{1}{n}\sum_{i=1}^n X_i^k.\] The $k$th sample moment can be regarded as an estimator for the $k$th population moment. Moreover, the $k$th sample moment will be unbiased for the $k$th population moment.

Given an observed sample it is possible to calculate specific values for any sample moment. We know that these estimators are unbiased for the corresponding population moments, and that the corresponding population moments are functions of the unknown parameter $\theta$. This motivates the method of moments estimation procedure.

Method of Moments Procedure

Suppose that a population is characterized by an unknown parameter, $\theta$. Suppose that $\theta$ has $L$ components. The goal is to estimate $\theta$ using a sample $X_1,\dots,X_n$. To proceed, the method of moments estimator, $\widehat{\theta}_\text{MoM}$, is calculated as follows:

Compute the first $L$ population moments, $m_1,\dots,m_L$ producing $L$ functions of $\theta$. Note, if any of the first $L$ population moments do not depend on $\theta$, continue computing these until there are $L$ equations.
Compute the $L$ sample moments, $\widehat{m}_1,\dots,\widehat{m}_L$, corresponding to each of the population moments computed.
For each $j = 1, \dots, L$, set \[m_j(\theta) = \widehat{m}_j.\]
Finally, simultaneously solve the $L$ equations for $\theta$.

The solution to these equations produces $\widehat{\theta}_\text{MoM}$.

Example 13.7 (Charles Estimates the Weight Distribution of Hockey Players) With a firmer understanding of estimation procedures, Charles returns to the earlier fascination regarding the weights of professional hockey players. In particular, Charles, making the assumption that the weights across the entire league are normally distributed with a mean of $\mu$ and a variance of $\sigma^2$, wants to estimate these values from a sample of $5$ observations.

Write down the method of moments estimators for $\mu$ and $\sigma^2$ in a normal population.
If Charles samples 188, 212, 181, 190, 225, 196, what are the estimated values for $\mu$ and $\sigma^2$?

Solution

First, we find the population moments. Note that $E[X] = \mu$. Moreover, we know that $\sigma^2 = E[X^2] - E[X]^2$, and so $E[X^2] = \sigma^2 + E[X]^2 = \sigma^2 + \mu^2$. Thus, taking $\widehat{m}_1$ and $\widehat{m}_2$ to be the first two sample moments, we get: \[\begin{align*} \mu &= \widehat{m}_1 \\ \sigma^2 + \mu^2 &= \widehat{m}_2 \\ \implies \sigma^2 &= \widehat{m}_2 - \mu^2 \\ &= \widehat{m}_2 - \widehat{m}_1^2. \end{align*}\] Thus, the estimators are $\widehat{m}_1$ and $\widehat{m}_2 - \widehat{m}_1^2$, respectively.
In this sample we can find that $\widehat{m}_1$ is given by 198.6667 and that $\widehat{m}_2$ is given by 39698.33. ⁷ Taking these values into the formula derived in the previous part gives an estimate for $\mu$ as 198.6667 and estimate for $\sigma^2$ as 229.8889.

Example 13.8 (Sadie’s Game) Sadie has started playing a new game with Charles. The game goes as follows. First, Sadie selects a random sized die, without Charles seeing the die. Then, Sadie will roll the die and flip a coin. If the coin comes up heads, the number that turned up on the die is told to Charles. If the coin comes up tails, the number is reported as a negative value. Charles does not see this process at all, and is just told that a string of numbers from a discrete uniform distribution between $-a$ and $a$ will be reported.

If Charles gets to hear $n$ numbers and then has to guess $a$, what is the method of moments estimator that could be used?
Suppose that Charles observes -5, 2, 3, 0. What is the method of moments estimate?

Solution

The first step is to derive the population moments. Note that for the discrete uniform on the interval between $a$ and $b$ we have \[E[X] = \frac{a+b}{2}.\] Thus, in this case that results in $E[X] = 0$. As a result, we must turn to the second population moment in order to use the method of moments estimators since $E[X]$ does not depend on $\theta$. To this end we have \[\text{var}(X) = \frac{(a - (-a) + 1)^2 - 1}{12} = \frac{(2a + 1)^2 - 1}{12}.\] Note that here, $\text{var}(X) = E[X^2]$, since $E[X] = 0$. Thus, we can set $\widehat{m}_2$ equal to this moment and solve for $a$. This gives \[\begin{align*} \frac{(2a + 1)^2 - 1}{12} &= \widehat{m}_2 \\ 4a^2 + 4a + 1 - 1 - 12\widehat{m}_2 &= 0 \\ a^2 + a - 3\widehat{m}_2 &= 0 \\ \implies a &= \frac{-1 \pm \sqrt{1 + 12\widehat{m}_2}}{2}. \end{align*}\] Since $a$ is positive, we need only consider the positive root in this case, giving $\widehat{a} = \dfrac{-1 + \sqrt{1 + 12\widehat{m}_2}}{2}$.
From this sample, the second sample moment is equal to 9.5. Thus, applying the result from above this would give estimates of either 4.8619.

Intuitively, this procedure takes the population moments, matches them to the sample moments, and defines the estimator to be the value of the parameter that equates these two sets of quantities. This is a reasonable sounding approach to derive estimators and, in practice, method of moments estimators perform quite well. Specifically, the method of moments estimators tend to be fairly robust to distributional assumptions, making them appropriate across a wide variety of populations and modelling scenarios. Beyond the robustness and intuitiveness, the method of moments estimators tend to be fairly performant, and are often easy to compute. All of these factors make this an attractive estimation technique in practice. With that said, there are some notable shortcomings of the method of moments procedure.

13.4.1 Shortcomings of the Method of Moments Procedure

There are three shortcomings of the method of moments procedures. Whether these shortcomings will override the utility and benefits of these techniques will depend on the specific scenario in which the estimators are being applied. The first concern is that, in order to calculate the method of moments estimators, we must assume that the population moments actually exist. While it is uncommon in practice, there are many distributions which do not have moments, or do not have all of their moments, and in these settings, it is not possible to use the method of moments technique at all. Second, the method of moments estimators tend to be biased for the true parameter values. This is not universally true, however, in most scenarios with even moderate complexity, the resulting estimators will not be unbiased. As discussed previously, the existence of bias does not disqualify an estimator from being useful or performant, however, it can be a shortcoming of the technique in certain settings. Finally, the estimates produced through the method of moments are not guaranteed to be valid estimates for the parameters. For instance, using method of moments estimators may result in variances that are negative, proportions greater than one, or other impossible estimates. These estimates can often be assessed to be evidently incorrect when they arise in practice, however, the fact that such estimates are possible at all can render the methods of moments to be of limited utility in certain scenarios.

13.4.2 Method of Moment Estimation in R

While it will often be the case that explicit forms for the method of moments estimators can be derived, this is not always straightforward, and not always desired. Instead, we may choose to leverage R to numerically work out the estimator for the method of moments, rather than doing so by hand. There are several possible approaches to this depending on the size of the parameter, $\theta$, that we wish to estimate as well as on the information that we already know. In particular, if $\theta$ is a single parameter then we can use a more straightforward technique compared to if $\theta$ is multidimensional. Further, we will differentiate the scenario where we know the closed form version of the population moments from those scenarios where we are only aware of the underlying distribution.

One Dimensional Parameter with Known Moment

In the simplest case we have a single dimensional parameter, $\theta$, and we know the population moments. In this case we can make use of the R uniroot function, which solves for the value of $x$ such that $f(x) = 0$ for some specified function. To use uniroot, we need to provide the function that we wish to solve for the root of, as well as an interval over which we are searching for a root. The idea is that we will define a function, \[f(\widehat{\theta}) = m_1(\widehat{\theta}) - \widehat{m}_1.\] The value for which $f$ is equal to $0$ will correspond to the value for $\widehat{\theta}$ that equates $m_1 = \widehat{m}_1$, which is what is required for a single dimensional parameter. Consider, for instance, the exponential distribution, characterized by a single parameter $\lambda$. The first moment of an exponential distribution is $\frac{1}{\lambda}$. In this case we will have $\theta = \lambda$ as a single dimensional parameter, and so we can use the following procedure.

One Dimensional Parameter with Unknown Moment

If the moment is unknown then it is often still possible to work out the method of moment estimator, however, it is required to use R to solve for the approximate moment(s) of the distribution in place of using the closed form solution. This will typically be less efficient, and there may be stability concerns with the computation, however, in many scenarios this will provide a quicker technique for approximating the solution. To do so we will make use of either sum for discrete distributions or integrate for continuous distributions. Note that if $X$ is discrete then \[E[X^k] = \sum_{x} x^kp_X(x),\] and if $X$ is a continuous random variable then \[E[X^k] = \int_{x} x^kf_X(x)dx.\] As long as we know either $p_X(x)$ or $f_X(x)$ then we can leverage R to directly compute these values. Consider the same example as above, without assuming knowledge of exp.moment1.

Notice that these estimates are effectively identical to the above estimates when the population moments were assumed to be known. Note that effectively the same procedure can be applied in the case of a discrete random variable however, instead of integrating over x, we form a vector of the outputs of $xp_X(x)$ and then sum over this. For instance, suppose that we have a hypergeometric distribution where we do not know the number of ‘success’ items, but we do know that there are $100$ items in total and that our sample will be of size $10$.

Multidimensional Parameters

The same general procedure can be applied when $\theta$ has more than one parameter. The changes that are required are two-fold. First, it is required to define multiple functions for the required population moments and, correspondingly, multiple equations to set to be equal to zero. Second, the uniroot function only applies for one dimensional equations, and so we must instead use a technique designed for higher dimensional solving. For instance, the multiroot function from the rootSolve package can be applied. Alternatively, we can turn this into an optimization rather than a root finding problem and apply optim. Beyond these changes the process is similar. The functions for population moments can either be explicitly encoded or approximated numerically, and the process will work whether there is a discrete or continuous random variable under consideration. While the procedure is conceptually straightforward, root finding and optimization in multiple dimensions can be fairly unstable computationally. As a result, it will often be the case that other tricks from computational statistics are required in order to accurately determine the roots of the functions, and in turn, solve for the method of moments estimation. For the interested, I would advise you looking into the documentation on multiroot and optim, however, a deeper exploration of these packages is beyond the scope of these notes.

Exercises

Exercise 13.1 Describe the difference between an estimator and an estimate.

Exercise 13.2 Suppose that a sample of size $250$ is drawn from a population with a distribution with mean $25$ and variance $5$. The sample mean, denoted $\overline{x}$, is found to be $23.3$. What is the probability that $\overline{x}$ is less than or equal to $25$?

Exercise 13.3 A set of $10$ houses in a particular area are being sampled to understand their weekly grocery expenses. Suppose that the average grocery spend during the week under study is denoted $\mu$. Moreover, suppose that in the sample of $10$ observations, the houses spend: $103$, $156$, $118$, $89$, $125$, $147$, $122$, $109$, $138$, and $99$.

Compute a point estimate for $\mu$.
Suppose that there are $10,000$ houses in this area. Let $\tau$ denote the total amount spent by all of these houses during the week. Estimate $\tau$ using the data collected. What estimator did you use?
Use the data given data to estimate $p$, the proportion of all houses that spend at least $100$ in a week on groceries.
Give a point estimate of the population median spend based on the sample. What estimator did you use?

Exercise 13.4 In a random sample of $80$ components of a certain type, $12$ are found to be defective.

Give a point estimate of the proportion of all such components that are not defective.
A system is to be constructed by randomly selecting two of these components and combining them in sequence. The connection will function if and only if both components function correctly. Estimate the proportion of all such systems that will work properly.

Exercise 13.5 Show that the estimator for the sample variance which divides by $n$ is biased. That is, \[S_n^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})^2,\] is a biased estimator of $\sigma^2$.

Exercise 13.6 Show that the sample variance estimator is unbiased. That is, \[S_{n-1}^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X})^2,\] is an unbiased estimator of $\sigma^2$.

Exercise 13.7 Suppose that we wish to estimate the population mean from a sample of size $n\geq 1$. We consider the two estimators, $\widehat{\theta}_1 = \overline{X}$ and $\widehat{\theta}_2 = X_1$.

Which estimator has a lower bias?
Which estimator has a lower variance?
Which is the better estimator?

Exercise 13.8 Suppose that a square plot of land with side length $\mu$ is desired. To form this plot, a long measuring stick of side length $\mu$ is used. The value of $\mu$ is unknown, and as a result, the area of the plots is unknown. In order to determine this, you make measurements of the measuring stick, denoted $X_1,\dots,X_n$. Assume that each $X_i$ is unbiased for $\mu$, with variance $\sigma^2$.

Is $\overline{X}^2$ an unbiased estimator for $\mu^2$?
Suppose you consider estimators of the form $\overline{X}^2 - kS^2$. What value of $k$ makes this an unbiased estimator?

Exercise 13.9 Let $X_1,X_2,\dots,X_n$ represent a random sample from the distribution \[f(x;\theta) = \frac{x}{\theta}\exp\left(-\frac{x^2}{2\theta}\right) \quad x > 0. \]

It can be shown that $E[X^2] = 2\theta$.⁸ Use this fact to construct an unbiased estimator of $\theta$ based on $X_1$.
Construct an unbiased estimator of $\theta$ based on $\sum_{i=1}^n X_i^2$.

Exercise 13.10 Consider a random sample $X_1,\dots,X_n$ from the pdf \[f(x;\theta) = 0.5(1+\theta x) \quad -1\leq x\leq 1.\] The value of $\theta$ falls in the range $[-1,1]$. Show that $\widehat{\theta} = 3\overline{X}$ is an unbiased estimator of $\theta$.

Exercise 13.11 Let $X_1,\dots,X_n$ be Bernoulli random variables, independently drawn, with success probability $p$. What is a method of moments estimator for $p$?

Exercise 13.12 Suppose that the proportion of allotted time that a randomly selected student spends working on a certain test is denoted $X$. Suppose that the pdf of $X$ is given by \[f(x;\theta) = \begin{cases} (\theta + 1)x^\theta & 0 \leq x \leq 1 \\ 0 & \text{otherwise} \end{cases}.\] Here we have $-1 < \theta$.

Use the method of moments to obtain an estimator of $\theta$.
Consider a sample of $10$ observations given by $0.92$, $0.79$, $0.90$, $0.65$, $0.86$, $0.47$, $0.73$, $0.97$, $0.94$, and $0.77$. What is an estimate of $\theta$?

Exercise 13.13 Suppose that $X \sim \text{Unif}(-\theta,\theta)$.

What is the method of moments estimator for $\theta$ based on a sample of size $n$?
Is this estimator unbiased for $\theta$?

Exercise 13.14 Show that the method of moments estimator for the mean of a distribution is unbiased.

Exercise 13.15 Are method of moments estimators always unbiased? Justify your answer.

For instance, the population being too large, us being resource constrained, it being a conceptual population without any finite representation, laziness… any of the usual culprits!↩︎
For instance, we may be interested in the population mean and as a result we compute the sample mean.↩︎
Thus, $\theta$ may be the value of the true mean in the population, or the variance, or the $75$th percentile. Any possible value that we could compute, if we had access to the full population, can be encompassed in this framework.↩︎
Note that it may not always be the case that a low variance is preferable, even between two estimators that have the same bias. Consider if the bias of two estimators is really bad. In this case, an estimator with low variance is guaranteed to give you an estimate that is really bad, in the sense that it will be far from the truth. On the other hand, a high variance estimator may give you an estimate that is really bad, however, the higher variability may also mean that it gives an estimate closer to the truth than would be feasible from the low variance estimator. This is not a typical case, and you would be ill-advised to rely on this high-bias/high-variance estimator in practice, but the example is useful to demonstrate the true concern with variance: it is less predictably close to its expected value.↩︎
It can be shown that, subject to the constraint that $\sum_{i=1}^n \omega_i = 1$, the sum of squares is minimized for $\omega_i = \frac{1}{n}$. This is an exercise that you can complete if you are familiar with Lagrange multipliers!↩︎
That is to say, problems where we seek the value that will maximize a function. If you have taken differential calculus, these types of questions are likely commonplace.↩︎
Note: this is not the sample variance. It is the mean of $X_i^2$. Thus, you square the data, and then average the results.↩︎
Try to show this!↩︎

13.1 The Role of Estimation, Estimators, and Estimates

13.2 Assessing the Performance of Estimators

13.2.1 The Bias of an Estimator

13.2.2 The Variance of an Estimator

13.2.3 The Mean Squared Error, Accuracy, and Precision

13.2.4 Conditions Beyond the Mean Squared Error

13.3 Procedures for Estimation

13.4 Method of Moments Estimators

13.4.1 Shortcomings of the Method of Moments Procedure

13.4.2 Method of Moment Estimation in R

One Dimensional Parameter with Known Moment

One Dimensional Parameter with Unknown Moment

Multidimensional Parameters

Exercises

Self-Assessment