15  The Basics of Null Hypothesis Significance Testing

15.1 The Framework of Null Hypothesis Significance Testing

Over the past two chapters the focus has been on estimation procedures for parameters of interest. Point estimation gives us methods to make inferences regarding the specific value of a particular parameter, while interval estimation permits the discussion of the uncertainty of these estimates. Taken together these estimation techniques allow for a deep understanding of the value of parameters, based on observed samples. We know that every sample we take is likely to result in different estimates based on sampling variability. Correspondingly, the specific inferences that are made regarding the parameter values will depend on the specific sample that is observed. Using interval estimates we hope to capture how uncertain our knowledge is, however, it is an unavoidable truth that any conclusions we draw are subject to the whims of the sample. A fundamental question we can ask, in light of this truth, is “how are we able to draw specific conclusions or make decisions on the basis of our estimated values?”

The framework of null hypothesis significance testing (NHST), often referred to as simply hypothesis testing, provides one mechanism for making decisions regarding the value(s) of parameter(s) using observed samples. In a hypothesis test the observed sample is used to weigh evidence against competing explanations for what is true in the population. We make educated guesses regarding the likely value of a population parameter and then determine how likely it would be to observe the sample that we have actually observed, if our guesses are actually true. If the sample is likely to be produced under our specified version of truth, then the sample provides no evidence against the guesses. If, on the other hand, the sample is unlikely given our specified version of the truth, this serves as evidence against our guesses.

Example 15.1 (Sadie and the Weighted Die) Sadie has been playing a board game that was borrowed from Garth, and has been feeling particularly unlucky based on dice rolls. Uncertain if the die provided in the game is actually fair, Sadie decides to test it. Specifically, in the game it benefits the player to roll high numbers and is a detriment to rolling low numbers. Sadie decides to roll the die many times, recording whether each roll is high (greater than or equal to \(3\)) or low (less than or equal to \(3\)).

1. Suppose Sadie rolls the die \(50\) times and observes \(21\) high values and \(29\) low values. If the die were fair, approximately how likely is it that \(21\) or fewer high values would be rolled in \(50\) rolls?
2. Suppose Sadie continues rolling, and in \(100\) rolls of the die, observes \(35\) high values and \(65\) low values. If the die were fair, approximately how likely is it that \(35\) or fewer high values would be rolled in \(100\) rolls?
3. In light of these probabilities, what is your conclusion about the die?

Solution

1. If the die were actually fair, then we know the number of high values should follow a \(\text{Bin}(50, 0.5)\). Thus, we want \(P(X \leq 21)\). We can compute this directly from the binomial (for instance, using R), which gives 0.161. Alternatively, we can use the normal approximation to the binomial. In this case, we would find that \(X\) share an approximate distribution with \(W \sim N(25, 12.5)\), and \(P(X \leq 21) \approx P(W \leq 21.5)\). Then, \[P(W \leq 21.5) = P(Z \leq \frac{21.5-25}{\sqrt{12.5}}) = \Phi(-0.99) \approx \Phi(-1).\] This can be approximated via the empirical rule as \[1 - (0.5 + \frac{0.68}{2}) = 0.16,\] which is near the value calculated directly from the binomial. Thus, there is about a \(16\%\) chance that the die would produce this few high numbers, if it were fair.
2. Using the exact same procedure as above, we get \(X \sim \text{Bin}(100, 0.5)\) approximated by \(W \sim N(50, 25)\). This gives either a direct binomial probability of approximately 0.002. For the approximation, we get \[P(W \leq 35.5) = P(Z \leq \frac{35.5 - 50}{5}) = \Phi(-2.9) \approx \Phi(-3).\] This is, from the empirical rule, approximately \[1 - (0.5 + \frac{0.997}{2}) = 0.0015.\]
3. Based on the \(100\) rolls of the die, it seems very unlikely that the die is actually fair. Sadie could be getting very unlucky, however, if the die is fair there is about a \(1\) in \(1000\) chance that this few high rolls would be seen. Thus, it is more reasonable to assume that the die is not actually fair than it is to assume that Sadie has just been very unlucky. The evidence after \(50\) rolls is far less strong, being approximately \(1\) in \(5\).

Definition 15.1 (Hypothesis Testing) Hypothesis testing is a statistical framework through which data are assessed to determine whether they sufficiently support a particular hypothesis regarding a population parameter. Under an assumed hypothesis regarding the true population parameter, the likelihood of observing the present sample is computed. From this, conclusions are drawn regarding the statistical validity of the hypothesis.

At the core of the hypothesis testing framework is the idea of a statistical hypothesis. A statistical hypothesis is a specification of a plausible parameter value made on the basis of subject-matter expertise, rather than through the data themselves. Alongside the statistical hypothesis, subject-matter expertise is required to define the evidentiary requirements of the test. Specifically, we must consider how certain we want to be regarding conclusions that we draw, a decision that is ultimately based on the stakes of drawing an incorrect conclusion. With the specification of a hypothesis and a required level of significance, we turn to the data that have been observed and summarize them using a test statistic. A test statistic is a statistic that has a known sampling distribution under the assumption that our hypothesis is correct. Using this test statistic, and the knowledge of its sampling distribution, we can assess the likelihood of having observed this specific statistic if the hypothesis were true. Based on our assessment, and the level of significance we desire, we can then draw conclusions and interpret the results.

This high-level description summarizes the procedure of hypothesis testing as a five-step procedure:

1. Determine the null and alternative hypotheses.
2. Determine the significance level for the test.
3. Compute the test statistic using the observed data.
4. Find the \(p\)-value based on the null sampling distribution.
5. Make a comparison, draw conclusions, and interpret the results.

Each of these steps is outlined in general in the following sections.

15.1.1 The Null and Alternative Hypothesis

At the core of the framework of hypothesis testing is the concept of statistical hypotheses. Specifically, hypothesis testing is fundamentally a procedure wherein evidence within a sample is assessed to determine whether it contradicts a particular hypothesis.

Definition 15.2 (Statistical Hypothesis) A statistical hypothesis is a statement regarding the value of an (unknown) population parameter, informed via outside knowledge rather than through estimation. For instance, we may state that \(\theta = 0\) or \(\theta \geq 10\).

In the framework of null hypothesis significance testing, we focus on the specification of two distinct hypotheses. First, and most importantly, we specify the null hypothesis. The null hypothesis corresponds to our underlying belief about the world prior to conducting statistical tests. The null hypothesis will capture how we will act without strong evidence to the contrary. In contrast to the null hypothesis, we also specify an alternative hypothesis. The alternative gives an alternative explanation compared to the null. That is, if the null is not true, then the alternative should be.

Definition 15.3 (Null Hypothesis) The null hypothesis is a statistical hypothesis that is meant to capture the assumed state of the world that would be believed without contradictory evidence. The null hypothesis captures the value of a parameter that is assumed to hold by default. Often, the null hypothesis captures the idea of no effect or no difference, such as taking \(\theta = 0\). The null hypothesis is typically denoted \(H_0\), so we write, for instance, \(H_0: \theta = 0\) or \(H_0: \theta \geq 10\).

Definition 15.4 (Alternative Hypothesis) The alternative hypothesis is a statistical hypothesis that is defined in contrast to a stated null hypothesis. Generally, we take the alternative hypothesis to be not the null. If the null hypothesis states \(\theta = 0\) then the alternative will be \(\theta \neq 0\). We denote the alternative as either \(H_1\) or \(H_A\). If the null hypothesis is not true, the alternative hypothesis will be.

When framing the null and the alternative hypothesis it is important to keep in mind that we are seeking evidence against the null hypothesis. We will never seek to positively confirm that the null hypothesis actually holds. Instead, we want to see if the observed data allow us to conclude that it certainly does not hold. For this reason, the hypotheses we are considering should be determined prior to data collection and should be informed by a subject-matter understanding, rather than for statistical convenience. To determine your null hypothesis, you should ask what you would continue to believe without evidence to the contrary, and take that as the null. If you have no such prior beliefs, then it is best to take the most conservative statement as the null hypothesis.¹

Example 15.2 (Sadie and Charles Care for Trees: Identifying Hypotheses) Sadie and Charles have, after watching a new documentary, become quite interested in caring for trees. They have started a small tree nursery, and are interested in how statistics may be used to inform their progress through this adventure. For each of the following questions, they are looking to identify what null and alternative hypotheses may be reasonable for the following questions.

1. They have found a pouch of aspen seeds, but are not sure where they came from. Aspens typically grow to be a total of about \(50\) feet tall, with a diameter of \(10.5\) inches. They want to know whether these aspens seeds are similar to common aspens, or not.
2. They have many different fertilizer options. They want to know whether a particular blend of their fertilizers influences the height to which the trees grow, or not.
3. They understand that bark beetles are a problem that can often impact pine trees. Before they help reforest in a certain area, they want to know whether more than \(10\%\) of pine trees are infested with bark beetles, or not, to understand whether new plants are likely to survive.

Solution

1. Here, we could think of running two separate hypothesis tests. If we take \(\theta_1\) to represent the average height of an aspen grown from the seed, we may test \(H_0: \theta_1 = 50\) versus the alternative \(H_A: \theta_1 \neq 50\). If \(\theta_2\) represents the average diameter of the grown aspens, then we can test \(H_1: \theta_2 = 10.5\) versus the alternative \(H_A: \theta_2 \neq 10.5\).
2. Here, we require a parameter, say \(\theta_3\), to represent the effect of the fertilizer on tree growth. Specifically, we may take \(\theta_3\) to represent the average change in height that a tree receiving the fertilizer has (compared to if the tree had not received the fertilizer). Then, it is most sensible to assume by default that there is no effect, and thus \(H_0: \theta_3 = 0\) versus \(H_A: \theta_3 \neq 0\).
3. Here, the parameter of interest is \(\theta_4\), the proportion of trees in a particular area that are infected with bark beetles. We may consider \(H_0: \theta = 0.1\) versus the alternative \(H_A: \theta \neq 0.1\). However, in this case, it may be more prudent to actually use a one-sided hypothesis, taking \(H_0: \theta \geq 0.1\) versus \(H_A: \theta < 0.1\). The rationale would be that, since the decision to act would only be influenced by a small value of \(\theta_4\), the true interest is in whether it is smaller than \(0.1\), not simply whether it is different from \(0.1\).

A hypothesis test is outlined by the collective statement of the null and alternative hypotheses. When deciding on the null and alternative, there is the possibility of considering either a one-tailed or a two-tailed hypothesis test. These refer to the number of tails of the distribution that would be considered evidence against the null hypothesis, or put differently, the number of tails captured by the alternative hypothesis.

Definition 15.5 (One-Tailed Hypothesis Test) In a one-tailed hypothesis test, the alternative hypothesis will take the form \(H_A: \theta > \theta_0\), or \(H_A: \theta < \theta_0\), for some constant value \(\theta_0\). In this sense, only one tail (either the upper tail in terms of \(\theta > \theta_0\) or the lower tail in terms of \(\theta < \theta_0\)) will be considered as evidence against the null hypothesis. In a one-tailed test, the null hypothesis is given as either \(H_0: \theta \leq \theta_0\) or \(H_0: \theta \geq \theta_0\).²

Definition 15.6 (Two-Tailed Hypothesis Test) In a two-tailed hypothesis test, the alternative hypothesis will take the form \(H_A: \theta \neq \theta_0\), for some constant value \(\theta_0\). In this sense, both the upper and lower tails will be considered as evidence against the null hypothesis. In a two-tailed test, the null hypothesis is given as \(H_0: \theta = \theta_0\).

As we continue to discuss the implementation of a hypothesis test and the practicalities in testing a particular hypothesis, we will discuss the implications in using one versus two tailed tests. The general guidance is that, unless there is a very strong, scientific rationale for considering a one-tailed test, two tailed tests ought to be preferred. If a one-tailed test is to be suggested, the null and alternative should still be specified prior to doing any analysis of the experiment, and which tail is tested should be informed through subject-matter expertise.³ Once the hypotheses have been selected, we need to make a choice regarding the levels of significance.

15.1.2 Significance Levels

In addition to specifying the hypotheses on the basis of subject-matter knowledge, to perform a hypothesis test we must also decide on the level of significance that we are considering. Generally, the level of significance refers to the amount of evidence that we would need against the null hypothesis in order to reject it (in favour of the alternative). This decision should be informed based on the stakes of the decisions that we are making. When the stakes are high, or it is very important to not reject the null hypothesis incorrectly, we should increase the amount of evidence we are looking for.

Definition 15.7 (Level of Significance) The level of significance, denoted \(\alpha\), is a measure of how much evidence is required to reject the null hypothesis in favour of the alternative. Formally, the level of significance specifies the probability of rejecting the null hypothesis, if it were actually true. In this sense, the lower the value of \(\alpha\), the stronger the evidence required against the null hypothesis. Typically, \(\alpha \leq 0.1\) is selected, with the specific value dependent on the context.

A fundamental truth of hypothesis testing⁴ is that we can never be certain in our conclusions. Owing to the inherent random nature of data, there is always the possibility that mistakes occur. The level of significance provides us with the capacity to control the likelihood of one class of these mistakes. Specifically, it controls how likely it is to conclude that the null hypothesis is not true when it is. In a perfect world, free of randomness and uncertainty, we would take \(\alpha = 0\). This way, we would never conclude that the null hypothesis should be rejected when it is actually true. Unfortunately, the only way to ensure that we never make this mistake is to never reject the null hypothesis.⁵ Instead, we take \(\alpha\) to be a small value greater than \(0\).

To decide what value specifically, we have to consider the question “What if we are wrong?”. If you incorrectly reject the null hypothesis, what are the stakes of that error? Consider a scenario where we are testing a new treatment for a severe illness, and we want to test whether the treatment has an effect on survival rates. In this case, we would typically take \(H_0: \theta = 0\) versus the alternative, \(H_A: \theta \neq 0\); by default we are assuming that the treatment does not have any impact, and are looking for evidence to the contrary. Now, suppose that there already exists a treatment for the illness that is moderately effective. In this setting, it is far more costly to make a mistake stating that the new treatment is also effective, if it turns out that it is not. The reason being that if we conclude the treatment is effective it may be prescribed to individuals, and this may happen in place of the existing effective treatment. If it turns out that the new treatment does not have a positive impact, this would mean that real people will receive treatments that are ineffective, when they could receive treatments that actually help. Conversely, if there does not exist any treatment at all for the illness now, we likely are willing to take a slightly higher risk. In this case, if we are wrong and the treatment does not meaningfully help, there is no alternative for the patient. As a result, in the first case we should take a lower value of \(\alpha\) compared to the second.

Example 15.3 (Sadie and Charles Care for Trees: Identifying Hypotheses) With the statistical hypotheses identified for their tree planting hobby, Charles and Sadie are now trying to determine what level of significance they should pick in running these hypotheses. Specifically, they are looking to rank the following hypotheses in order of required significance levels, and justify these choices to one another.

1. They have found a pouch of aspen seeds, but are not sure where they came from. Aspens typically grow to be a total of about \(50\) feet tall, with a diameter of \(10.5\) inches. They want to know whether these aspens seeds are similar to common aspens, or not. Importantly, they have decided that they will plant the aspens no matter what they find, and care for them all the same. Because they do not know where the seeds came from, they cannot change suppliers even if they wanted to.
2. They have many different fertilizer options. They want to know whether a particular blend of their fertilizers influences the height to which the trees grow, or not. The mix of fertilizer that they are considering here is cheaper than their current fertilizer choice, and so they have a desire to switch if possible. However, they know that the current fertilizer they use is effective at increasing growth.
3. They understand that bark beetles are a problem that can often impact pine trees. Before they help reforest in a certain area, they want to know whether more than \(10\%\) of pine trees are infested with bark beetles, or not, to understand whether new plants are likely to survive. If they plant trees into an infested area, these trees will likely all die relatively young, wasting resources and the ability to help revitalize the ecosystem.

Solution

These hypotheses require evidence in the order that they are currently written. Namely, hypothesis (a) requires less than (b) which requires less than (c).

• For (a), the hypothesis test is mostly for intrigue. It will not alter the way that Sadie and Charles act in any way, nor are there any stakes to the decision. As a result, if they are wrong, that is okay – the only impact of this is that they may tell people they found aspen seeds that grow differently compared to regular, when they have not actually done so.
• Next, is (b). The stakes here are higher since there currently exists a fertilizer that works well. If Sadie and Charles conclude that the new fertilizer also improves growth, but it does not, then they will end up with plants that are worse off than they otherwise would be had they not made the same conclusion. Fortunately, however, the fertilizer is less costly than the current one. As a result, the mistake, while impacting the growth of their trees, will not have cascading negative outcomes.
• Finally, hypothesis (c) is the hypothesis with the largest stakes. If they draw the wrong conclusion in this case, they are risking resources and opportunity. Additionally, if they find that the infestation is bad, they have remedies for this, and as such, it is important to draw the correct conclusion here.

The Historical Case for \(\alpha = 0.05\)

There is a long tradition, one which persists across many fields today, of taking \(\alpha = 0.05\), regardless of the situation. This tendency owes itself to early work by Ronald Fisher (a statistician largely responsible for our approach to statistical inference). In Statistical Methods for Research Workers, published in 1925, Fisher wrote “It is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not. Deviations exceeding twice the standard deviation are thus formally regarded as significant.” In 1926, Fisher further wrote “If one in twenty does not seem high enough odds, we may, if we prefer it, draw the line at one in fifty (the \(2\) per cent point), or one in a hundred (the \(1\) per cent point). Personally, the writer prefers to set a low standard of significance at the \(5\) per cent point, and ignore entirely all results which fail to reach this level. A scientific fact should be regarded as experimentally established only if a properly designed experiment rarely fails to give this level of significance.”

Fisher largely worked in well-designed experiments applied to the study of agriculture. It is probably prudent to read Fisher’s advice of the \(5\%\) level of significance as existing in this context. Even as the originator of taking \(\alpha = 0.05\), Fisher acknowledged the importance of selecting a line based on the needs of the particular context. It is a somewhat unfortunate historical artifact that his declarative statements of \(\alpha = 0.05\) took far stronger hold on the scientific world at large, as compared to his more contextual statements. Still, with our present understanding of hypothesis testing, we should always keep in mind the context of the question we are asking, and determine an appropriate level of significance within this context.

Once a level of significance has been decided upon, we need to determine a method for establishing how we can assess whether the evidence in the sample achieves the level of significance or not. To do so, we rely on test statistics.

15.1.3 Test Statistics

Test statistics are statistics⁶ with a special property. Notably, if the null hypothesis is true, a test statistic must have a known distribution, with all parameter values known as well. That is, if the sampling distribution of a statistic is fully specified assuming that the null hypothesis holds, this statistic is a test statistic.

Definition 15.8 (Test Statistic) A test statistic is any statistic, which is to say a quantity computable given a specific sample, used for hypothesis testing. Test statistics must have the property that, supposing the null hypothesis is true, the sampling distribution of the statistic is completely specified. Often, the exact sampling distribution will not be known, but a statistic can still be regarded as a test statistic if an approximate distribution is available.

Definition 15.9 (Null Distribution) The sampling distribution of a test statistic, assuming the null hypothesis holds, is referred to as the null distribution. We may also say that the statistic follows a particular distribution, under the null. Suppose that \(\widehat{\theta}\) is a test statistic with a null distribution \(F\), then we can write \(\widehat{\theta} \stackrel{H_0}{\sim} F\), to mean that, under the null, the statistic follows the distribution given by \(F\).

Because the null distribution is fully specified, it is possible to calculate probabilities associated with test statistics assuming that the null hypothesis holds. These probabilities will ultimately be assessed as evidence in relation to the level of significance. Typically, a test statistic can be derived by first considering a statistic, and then introducing dependence on the unknown parameters that are being tested. While these parameter values are unknown, generally speaking, if the null hypothesis is assumed to be true this will specify concretely the value of the parameter. For instance, suppose that we have a sample from a normal distribution, with a known variance (\(\sigma^2\)) but an unknown mean (\(\mu\)). We know that the sample mean will have a normal sampling distribution, giving \(\overline{X} \sim N(\mu,\sigma^2)\). If we wish to test the null hypothesis \(H_0: \mu = \mu_0\), for some constant \(\mu_0\), then the null distribution of \(\overline{X}\) becomes \(N(\mu_0, \sigma^2)\). This stands as a test statistic since we exactly know the distribution under the null. More commonly we may take \(\overline{X} - \mu_0\), resulting in \(N(0, \sigma^2)\), or even \[\frac{\overline{X} - \mu_0}{\sigma} \stackrel{H_0}{\sim} N(0,1).\]

In each case, the statistic has a known null distribution. As a result, we can solve for probabilities assuming that the null hypothesis were true. These probabilities are most commonly codified through the use of p-values.

15.1.4 \(p\)-values and Critical Values

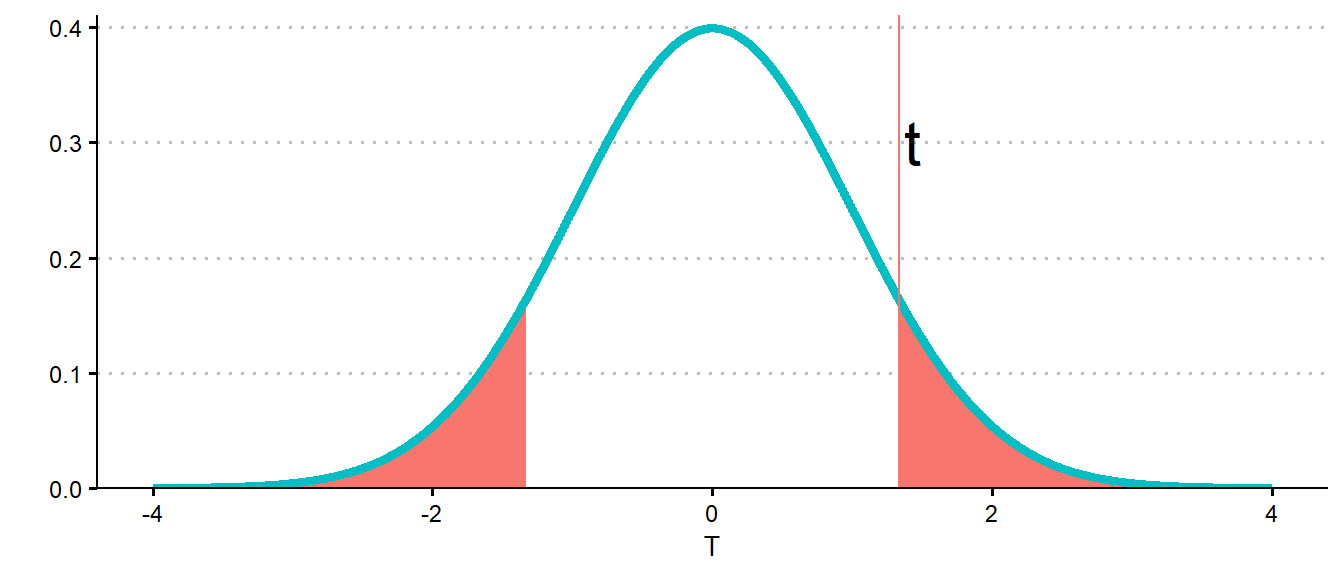
To determine whether there is sufficient evidence to contradict the assumed null hypothesis, we must be able to translate statements regarding our test statistic into probability values. Specifically, we can “ask what values for our test statistic could we have observed that would have been at least as contradictory to the null hypothesis as the value that we did observe?”. Then, using the null distribution, we can ask, “assuming the null hypothesis were true, how likely would it have been to observe an outcome of the test statistic at least as contradictory as the outcome we did observe?”. The probability associated with this is called the \(p\)-value.

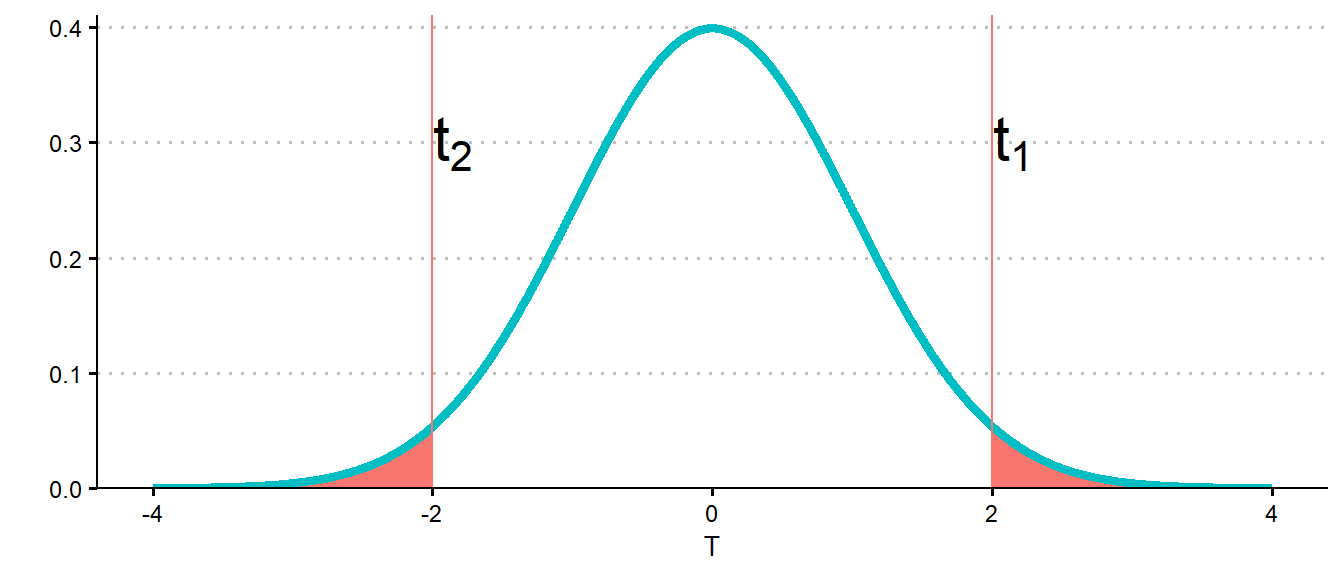
Definition 15.10 (\(p\)-value) The \(p\)-value, (or probability value), is a measure of how likely the observed data are, assuming that the null hypothesis is true. Specifically, the \(p\)-value measures the probability of observing an outcome at least as extreme⁷ as the outcome that was observed, based on the test statistic. This probability indicates how likely the data were to be observed by random chance, assuming the null hypothesis holds.

Suppose, for sake of example, we observe a value of a test statistic, \(t=-2\). Under the null hypothesis, we know that \(t\) should equal \(0\). Then, we ask “what could we have observed that would have been more contradictory than what we did observe?” Suppose that we are considering a two-tailed alternative. Note that if we had observed any value of \(t < -2\), this would have been more extreme. On the other hand, had we observed any value of \(t \geq 2\), this also would have been more extreme. Thus, any value outside the interval \((-2, 2)\) would have been more extreme. Thus, to work out the \(p\)-value in this case we would find \[P(\{T \leq -2\}\cup\{T \geq 2\}) = P(T \leq -2) + P(T \geq 2).\] Had this been a one-tailed test, the \(p\)-value would have been only \(P(T \leq -2)\).

Intuitively, the smaller the \(p\)-value, the more evidence against the null hypothesis based on the sample. If the \(p\)-value were sufficiently low, then it would be the case that the observation we made would be sufficiently rare, assuming the null hypothesis were true. With a small enough probability, it is more reasonable to assume that the null hypothesis is not accurate, rather than assuming that we happened to make a particularly rare observation. To decide how small of a probability is small enough, we turn to our level of significance. If the \(p\)-value is below the selected level of significance, then we can conclude that the results are unlikely to have been observed due to chance, and instead, it is more likely to be observed as the alternative is a better explanation of the underlying reality. On the flip side, if the \(p\)-value is larger than the level of significance, then we did not see sufficient evidence in the sample to reject the null hypothesis.

Example 15.4 (Sadie and Charles Care for Trees: Identifying \(p\)-Values) Charles and Sadie are feeling quite confident in their application of hypothesis testing for tree care. They have decided on hypotheses, significance levels, and have even worked out what test statistics they will use. Now, they are hoping to practice calculating \(p\)-values before the data collection actually begins, to ensure that they will be able to do it later on, when it matters. Determine the \(p\)-values based on the given information in the following.

1. For the pouch of aspen seeds, they are planning to test \(H_0: \theta_1 = 50\) versus \(H_A: \theta_1 \neq 50\). This will be done using the test statistic \[T_1 = \frac{\overline{X} - 50}{10/\sqrt{n}} \stackrel{H_0}{\sim} N(0,1).\] Suppose than in a sample of size \(4\) they find \(\overline{x} = 60\). For the diameters, testing \(H_0: \theta_2 = 10.5\) versus \(H_A: \theta_2 \neq 10.5\), they will take \[T_2 = \frac{\overline{X} - 10.5}{3/\sqrt{n}} \stackrel{H_0}{\sim} N(0,1).\] Suppose in a sample of size \(9\) they observe \(\overline{x} = 8.5\).
2. To understand the effects of their fertilizer types, they will test \(H_0: \theta_3 = 0\) versus \(H_A: \theta_3 \neq 0\). They will use the statistic \[T = \frac{\overline{X}}{s/\sqrt{n}} \stackrel{H_0}{\sim} t_{n-1}.\] In a sample of \(49\) trees, they observe \(\overline{x} = 3\), with a sample standard deviation of \(14\).
3. To investigate the extent of the bark beetle infestation, they will test \(H_0: \theta_4 \leq 0.1\) versus \(H_A: \theta_4 > 0.1\). This can be done via \[T=\frac{\widehat{p} - 0.1}{\sqrt{0.1(0.9)/n}} \stackrel{H_0}{\sim} N(0,1).\] In a sample of size \(100\) they observe \(14\) trees that are infected.

Solution

1. Using \(T_1\), we find an observed value, \(t_1\) by plugging in \(n=4\) and \(\overline{x} = 60\). This gives \(t_1 = 10/5 = 2\). As a result, the \(p\)-value is given by \[P(Z \geq 2) + P(Z \leq -2) = 1 - \Phi(2) + \Phi(-2) = 2(1 - \Phi(2)) \approx 0.046.\] Alternatively, we could have used the empirical rule to conclude that this will be approximately \(0.05\). For \(T_2\), plugging in \(n=9\) and \(\overline{x} = 8.5\) gives \(t_2 = -2/1 = -2\). Thus, for the \(p\)-value we would get the exact same quantity, since we need \(P(Z \leq -2) + P(Z > 2)\). Consider the following plot that shades the area needed to calculate the \(p\)-value, with \(t_1\) and \(t_2\) each labelled.

2. Here, taking \(n=49\), \(\overline{x} = 3\), and \(s = 14\). Thus, \[t = \frac{3}{14/\sqrt{49}} = \frac{3}{2} = 1.5.\] To calculate a \(p\)-value, we make reference to the \(t_{48}\) distribution, taking \(F\) to be its CDF, this gives \[P(T \leq -1.5) + P(T > 1.5) = F(-1.5) + (1 - F(1.5)) = 2F(-1.5) \approx 0.14.\] The corresponding area is identified in the following figure.

3. Here, the observation has been \(\widehat{p} = 14/100 = 0.14\), with \(n=100\). Thus, \(t = 0.04/0.03 = 4/3\). The \(p\)-value here is given by \[P\left(Z \leq \frac{-4}{3}\right) + P\left(Z \geq \frac{4}{3}\right) = \Phi\left(\frac{-4}{3}\right) + \left(1 - \Phi\left(\frac{4}{3}\right)\right) = 2\Phi\left(\frac{-4}{3}\right) \approx 0.182.\] The following plot shades the relevant region.

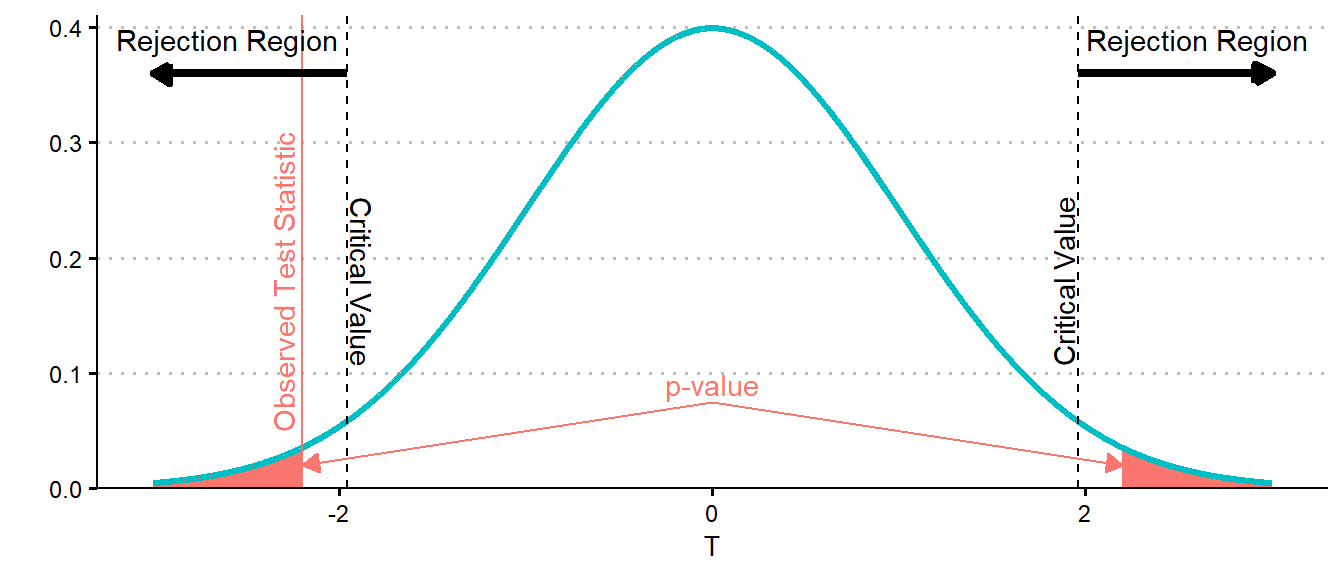
The \(p\)-value can be interpreted as the level of significance at which the observed data contradict the null hypothesis. In this sense, the \(p\)-value serves as a measure of how strong the evidence against the null hypothesis will be. An alternative method for the same mathematical approach is to determine how large of a test statistic value would need to be observed in order to achieve a \(p\)-value equal to the level of significance. If we observe a test statistic that is larger than this value that is then equivalent to observing a \(p\)-value which is smaller (and vice versa). This value is known as a critical value.

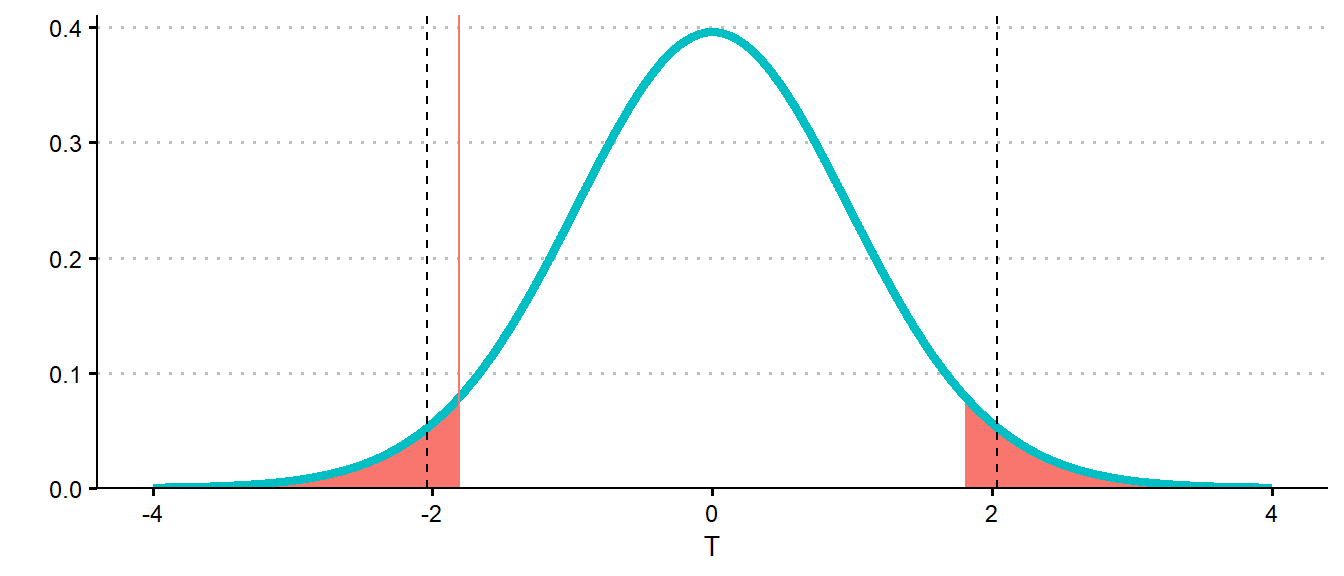
Definition 15.11 (Critical Value) A critical value is the value, derived through a null distribution, at which the corresponding \(p\)-value coincides with the significance level. That is, the critical value is the value, \(t^*\), such that \[P(T \leq -t^*) + P(T \geq t^*) = \alpha,\] assuming a two-tailed hypothesis test, where \(T\) is the statistic of interest, and the probability is taken with respect to the null distribution.

The critical values are related to the percentiles of a distribution. Specifically, if \(T\) has a symmetric distribution⁸ then the critical value for a significance level \(\alpha\) exactly coincides with the \(1-\alpha/2\) percentile of the distribution. We saw these critical values being used when discussing confidence intervals, if we substitute the confidence level \(p=1-\alpha\). If a critical value of \(t^*\) is found then if we observe \(t\) such that \(|t| > t^*\), this is equivalent to observing a \(p\)-value that is less than \(\alpha\). The \(p\)-value provides more information than a comparison to a critical value, however, the critical value technique can be easier to leverage for quick calculations, particularly when you are away from a computer.

Example 15.5 (Sadie and Charles Care for Trees: Identifying Critical Values) While they had some success identifying the \(p\)-values, Charles and Sadie realize that the conclusions that the calculations for the \(p\)-values are highly dependent on what values they assumed they would see. However, if they approached the problems via critical values, this will be relevant as long as the null distributions are correct. For each scenario, they wish to identify the critical value associated with the given hypothesis test.

1. For the pouch of aspen seeds, they are planning to test \(H_0: \theta_1 = 50\) versus \(H_A: \theta_1 \neq 50\). This will be done using a test statistic with a null distribution of \(N(0,1)\), at \(\alpha = 0.1\). For the diameters, testing \(H_0: \theta_2 = 10.5\) versus \(H_A: \theta_2 \neq 10.5\), they will use the same null distribution and significance level.
2. To understand the effects of their fertilizer types, they will test \(H_0: \theta_3 = 0\) versus \(H_A: \theta_3 \neq 0\). They wish to take \(\alpha = 0.05\), and use a test statistic with \(t_{n-1}\) degrees of freedom. They suspect the sample size will be \(49\).
3. To investigate the extent of the bark beetle infestation, they will test \(H_0: \theta_4 \leq 0.1\) versus \(H_A: \theta_4 > 0.1\). Here, they require a significance level of \(\alpha = 0.01\).

Solution

1. Since these tests use the same significance levels, they will have the same critical values. Notably, we require \(\Phi(-t^*) + 1-\Phi(t^*) = \alpha\), which is equivalent to saying \[\Phi(-t^*) = \frac{\alpha}{2} \implies t^* = -Z_{0.1/2} \approx 1.64.\]
2. For this test, taking \(F(t)\) to represent the cumulative distribution function for a \(t_{48}\) distribution, we require \(F(-t^*) + 1 - F(t^*) = \alpha\), which is equivalent to saying \[F(-t^*) = \frac{\alpha}{2} \implies t^* = -F^{-1}(\frac{0.05}{2}) = -t_{n-1,0.025} \approx 2.01.\]
3. For this test, the critical value must satisfy \(1 - \Phi(t^*) = \alpha\), which is equivalent to \[\Phi(-t^*) = \alpha \implies t^* = -Z_{0.01} \approx 2.33.\]

With either the \(p\)-value calculated or the critical value for comparison, it is possible to draw scientific conclusions from the hypothesis test.

15.1.5 Drawing Conclusions and Interpretation

By comparing the calculated \(p\)-value to the level of significance, or the calculated test statistic to the critical value, we are able to draw conclusions from the hypothesis test. Our conclusion will provide an answer to whether we reject or fail to reject the null hypothesis. Specifically, if the \(p\)-value is less than the level of significance, or the observed test statistic is less than the critical value⁹ then we can reject the null hypothesis, in favour of the alternative. We call the region of observations where we reject the null hypothesis the rejection region (see Figure 15.1). Practically this means that the level of evidence contradicting the null hypothesis in the observed data exceeds the level of evidence we needed to see, in the given context, in order to act as though the null hypothesis is not true. If the \(p\)-value is larger than the level of significance (or equivalently, if the critical value does not fall into the rejection region) then we fail to reject the null hypothesis. This means that our sample did not contain sufficient contradictory evidence to the null hypothesis, based on the context of the situation.

Figure 15.1: The labelled components of a hypothesis test. The observed test statistic is either compared to the critical values to see whether it falls into the rejection region or not. In a one-sided hypothesis test, the rejection region is one-sided as well. Alternatively, the area under the null distribution outside of the observed test statistic (in both tails, as depicted here, for a two-sided hypothesis test; in a single tail for a one-sided hypothesis test) can be computed as the \(p\)-value. The \(p\)-value is then compared to the level of significance.

Note, it is not possible in the hypothesis testing framework to accept the null hypothesis. This is because our level of evidence is always assessed for the degree to which it contradicts the null hypothesis. If our observations are unlikely assuming that the null hypothesis is true, it is reasonable for us to act as though the null hypothesis is not true. If, on the other hand, our observations do not contradict the null hypothesis, we will continue to act as though it were true, even though we have not built up positive evidence in its favour.

When we reject the null hypothesis, we often say that the result is statistically significant at the \(\alpha\) significance level. Statistical significance is a measure of strength of evidence against the null hypothesis.

Definition 15.12 (Statistical Significance) A result is said to be statistically significant if the null hypothesis is rejected. Specifically, the result is said to be statistically significant at a set level of significance, though, this is often implied from context. A result is said to be not statistically significant if the null hypothesis is not rejected.

Example 15.6 (Sadie and Charles Care for Trees: Drawing Conclusions) Charles and Sadie have managed to calculate test statistics, \(p\)-values, and critical values for the hypothesis tests that they established. All that is left is for them to interpret what these test results actually mean. They are looking to draw and interpret conclusions, based on the following information, and ideally, they would do this both using \(p\)-values and critical values.

1. For the pouch of aspen seeds, they are testing \(H_0: \theta_1 = 50\) versus \(H_A: \theta_1 \neq 50\), using \[T_1 = \frac{\overline{X} - 50}{10/\sqrt{n}} \stackrel{H_0}{\sim} N(0,1).\] In a sample of size \(4\) they find \(\overline{x} = 60\). For the diameters, they test \(H_0: \theta_2 = 10.5\) versus \(H_A: \theta_2 \neq 10.5\), using \[T_2 = \frac{\overline{X} - 10.5}{3/\sqrt{n}} \stackrel{H_0}{\sim} N(0,1).\] In a sample of size \(9\) they observe \(\overline{x} = 8.5\). They wish to use \(\alpha = 0.1\) level of significance.
2. To understand the effects of their fertilizer types, they test \(H_0: \theta_3 = 0\) versus \(H_A: \theta_3 \neq 0\) using \[T = \frac{\overline{X}}{s/\sqrt{n}} \stackrel{H_0}{\sim} t_{n-1}.\] In a sample of \(49\) trees, they observe \(\overline{x} = 3\), with a sample standard deviation of \(14\). They wish to use \(\alpha = 0.05\) level of significance.
3. To investigate the extent of the bark beetle infestation, they test \(H_0: \theta_4 \leq 0.1\) versus \(H_A: \theta_4 > 0.1\) using \[T=\frac{\widehat{p} - 0.1}{\sqrt{0.1(0.9)/n}} \stackrel{H_0}{\sim} N(0,1).\] In a sample of size \(100\) they observe \(14\) trees that are infected. They wish to use \(\alpha = 0.01\) level of significance.

Solution

1. From the previous examples we found that the \(p\)-value was approximately \(0.046\) for both tests. Since \(p < \alpha\), we can reject the null hypothesis, and we conclude that, based on the sample, there is sufficient evidence to conclude that the heights and diameters of the found aspen seeds are different from average aspen seeds. These results are statistically significant at the \(0.1\) level of significance. Alternatively, we could use the critical value of \(1.64\). Since \(t_1 = 2 > 1.64\), and since \(t_2 = -2\), so \(|t_2| > 1.64\), both statistics fall into the rejection region, and we reject the null hypothesis at the \(0.1\) level of significance.

2. Here we find \(p = 0.14\). Since \(p > \alpha\), we fail to reject the null hypothesis at the \(\alpha = 0.05\) level of significance. Thus, we conclude that there is insufficient evidence in the sample to conclude that the fertilizer has a non-zero effect on growth. Alternatively, we can consider that \(t = 1.5\), compared to a critical value of \(2.01\). Since \(t < 2.01\), the statistic does not fall in the rejection region, and we fail to reject the null hypothesis.

3. The \(p\)-value was found to be \(0.182\). Since we are testing at a \(0.01\) level of significance, \(p > \alpha\), and so we fail to reject the null hypothesis. As a result, there is insufficient evidence, based on the sample, to conclude that more than \(10\%\) of the pine trees are infected by bark beetles. Alternatively, we consider the critical value to be \(2.33\). Here, note that since this is a one-tailed test, the rejection region is only the values of \(t\), such that \(t > 2.33\). Because \(t < 2.33\) we fail to reject the null hypothesis.

Statistical significance is the foundational language of scientific inquiry. Specifically, results that are statistically significant are typically held up as actual results, where those that are not statistically significant are treated as though they are the result of random noise. In order for a claim to be scientifically justified, it must be statistically significant. However, it is important to note that statistical significance is not a measure of how big or meaningful a particular effect will be. Instead, it is a measure of how strong the evidence for believing a result is. That is, you can have statistically significant findings that are not particularly meaningful. For instance, suppose that the parameter of interest is the effect of a medical treatment on life expectancy. If we find that the treatment improves the life expectancy for patients, and that this result is statistically significant we do not know whether the treatment improves the life expectancy by a lot or a little. All we know, in this context, is that there was strong evidence in the sample that the treatment actually did improve the outcome in this case.

15.2 Errors in Hypothesis Testing

When conducting a hypothesis test we are still dealing with uncertainty. As a result it is always possible that the conclusions that are drawn will be incorrect. By selecting an appropriate level of significance, and by selecting a test statistic with a known null distribution, we hope to minimize the possibility of errors. However, random variation can still lead to incorrect conclusions. When considering errors in the conclusions of a hypothesis test, there are two types of errors that can be made. We can either reject a null hypothesis that is actually true, or else we can fail to reject a null hypothesis that is actually false. These are¹⁰ referred to as Type I and Type II errors, respectively.

Definition 15.13 (Type I Error) A type I error is a false positive. This occurs when the null hypothesis is rejected, but the null hypothesis is actually true.

Definition 15.14 (Type II Error) A type II error is a false negative. This occurs when the null hypothesis is not rejected, but the null hypothesis is actually false.

Both type I and type II errors are problematic, and test procedures are preferable when they minimize the probabilities of each error type. Focusing on the probability that a type I error occurs, we can determine how likely this is by asking what the probability of rejecting the null hypothesis is, assuming that the null is true. That is, under the null hypothesis, what is the probability that we observe a statistic beyond the critical value? By definition, this is given by the level of significance. That is, the probability of a type I error is exactly equal to the level of significance, \(\alpha\).

This gives an alternative method of interpreting the value of \(\alpha\). Specifically, the value of \(\alpha\) is the probability of making a false positive claim. Intuitively, we want this to be as small as possible, and so taking \(\alpha\) to be smaller seems reasonable. Unfortunately, the probability of making a type I error tends to be inversely correlated with the probability of making a type II error. The probability of a type II error is, typically, less straightforward to determine. For it, we need to determine the probability, assuming that the null hypothesis is actually false, that we fail to reject the null. That is, under the alternative hypothesis, what is the probability that we observe a statistic value that is less than the critical value. While this is a challenging probability to determine¹¹ explicitly, we give this the label \(\beta\). If we consider the probability \(1-\beta\), this gives the probability of rejecting the null hypothesis when it is actually false, a true rejection. This is a quantity of particular interest in hypothesis testing, and as such, we refer to it as the power of a hypothesis test.

Definition 15.15 (Power) The power of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is, in fact, false. That is it gives the probability of a true rejection. The power of a test generally gives a measure of how well a test is able to detect true effects. Typically, the power of a test is denoted by \(1-\beta\), where \(\beta\) gives the probability of a type II error.

A hypothesis test would ideally have a low probability of a type I error, which is to say a low level of significance, and a corresponding high power. Unfortunately, typically as the level of significance of a test decreases, so too does the power, and vice versa. As a result, in any hypothesis testing scenario there is a need to make a deliberate trade-off between the level of significance and the power. Typically, hypothesis testing proceeds by selecting an appropriate level of significance for the given setting, and then among tests that achieve this level of significance, searching for a test with the highest power. This way the type I errors are controlled at a set level, and the type II errors are minimized. By recognizing that the probabilities of type I and type II errors need to be balanced against one another, it is possible to more intentionally select an appropriate level of significance. Specifically, it is worth thinking through, in any given setting, whether the prospect of a false positive or a false negative is a worse outcome, and then balancing the selected rates accordingly.

Table 15.1: Conclusions and errors of hypothesis testing.

	\(H_0\) is True	\(H_0\) is False
\(H_0\) is Rejected	False Positive Type I Error (\(\alpha\))	True Positive Power (\(1-\beta\))
\(H_0\) is Not Rejected	True Negative	False Negative Type II Error (\(\beta\))

Example 15.7 (Charles and Sadie Care for Trees: Possible Errors) With an understanding of how they can draw conclusions using null hypothesis significance testing, Charles and Sadie turn to questioning “what if we are wrong?” Specifically, they want to think about different hypothesis tests that they can run as they continue their tree nursery, with a focus on understanding what a type I or type II error would refer to in each case, and whether they should prioritize a low level of significance or a high power for the corresponding tests.

1. Charles and Sadie wish to consider whether the germination rate of a new seed variety is any different from the historical average. The new seed is more expensive than historical seeds, and they are not currently displeased with the seeds that they have been using.
2. They wish to investigate whether a new fertilizer that is substantially cheaper than their current fertilizer is offered. They wish to test whether there is an improvement of the new fertilizer, compared with the old one.
3. Charles is told of a new treatment that promises to increase the disease resistance in seedlings. The treatment is relatively affordable, and does not seem to have any negative impacts, but they are concerned that it may not actually work.
4. Sadie has been researching techniques for protecting plants through the winter. Their current strategy works reasonably well, but Sadie thinks that with a little more investment, they may be able to improve this dramatically.

Solution

1. In this case, a Type I error represents the conclusion that the new seed variety differs from the historical average when, in fact, it does not. A type II error would occur if Sadie and Charles fail to reject the null hypothesis, concluding that there is no evidence of a difference between the current and historical seeds, when such a difference really does exist. Because they are currently happy with their current seeds, and because the new seeds are more expensive, they would want to be very certain that the new seeds are in fact different if they are going to switch. As a result, they should be considering a lower level of significance here, reducing the probability of type I error.

2. In this case, a Type I error occurs if they conclude the new fertilizer is improved, if it really is not an improvement, where the type II error occurs if they see no evidence of improvement when there really is. Because the fertilizer is cheaper, they would save money if they managed to switch, and thus it is important for them to identify if there really is an improvement. Missing an improvement that exists is a costly mistake, and so they should prioritize higher power in order to minimize the negative consequences associated with missing out.

3. In this case, a Type I error occurs if they conclude that the treatment actually does increase the resistance to diseases in plants, when it does not in actual fact. A type II error would occur if they conclude that there is no evidence for suggesting that the treatment reduces diseases, but it actually does. Here, because the treatment is affordable and seems otherwise harmless, it is worse to conclude that it does nothing if it actually works compared to concluding that it does nothing if it does not. As a result, a higher power is preferable.

4. In this case, a Type I error occurs if they conclude that the new strategy works better than the old strategy, when it does not. Type II errors occur if the new strategy works better, but they do not find sufficient evidence to conclude this in the sample. Here, they currently have a functioning strategy, and it would cost more to move to a new one. As a result, they need to make sure that if they do move, it is an improvement. This corresponds to a lower level of significance.

15.3 Hypothesis Testing for Population Means

The general procedure for hypothesis testing is versatile and applies in a wide range of scenarios. Whenever there is a need to test a particular parameter, the outlined steps can be followed and, supposing that an appropriate test statistic is found, a valid hypothesis test will be derived. With that said, there are several parameters that are tested with enough frequency that the corresponding hypothesis testing procedures are worth studying specifically. In the following sections, we outline the specific procedures for testing hypotheses relating to population means and proportions. These procedures are specific instantiations of the previously outlined procedures, and serve as example use cases for the overarching framework of hypothesis testing.

15.3.1 \(Z\)-Tests for Population Means in Normal Populations

Suppose that we are interested in testing hypotheses relating to the mean of a normal distribution, with a known variance. In this context, we have that \(X_1,\dots,X_n \sim N(\mu, \sigma^2)\), where \(\mu\) is unknown. We have seen that the sample mean, \(\overline{X}\), has a sampling distribution given by \(N(\mu,\dfrac{\sigma^2}{n})\). As a result, suppose that we wish to test the null hypothesis \(H_0: \mu = \mu_0\). Then, assuming the null hypothesis holds, we must have that \(E[\overline{X}] = \mu_0\), and more specifically, \[T = \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}} \stackrel{H_0}{\sim} N(0, 1).\] Suppose that we observe \(T = t\), then owing to symmetry we can compute the relevant \(p\)-value as \[P(T \leq -|t|) + P(T \geq |t|) = P(Z \leq |t|) + (1 - P(Z \leq -|t|)) = 2\Phi(-|t|).\] If, instead, we had wished to use the critical value method, then we would need to solve \[2\Phi(-t^*) = \alpha \iff t^* = Z_{1-\alpha/2},\] where \(Z_{1-\alpha/2}\) is the critical value of the standard normal. If instead a one-tailed hypothesis test were run, we would take the \(p\)-value to be \(\Phi(t)\) (or \(1-\Phi(t)\)), and the critical value as either \(Z_{\alpha}\) or \(Z_{1-\alpha}\), depending on whether the upper or lower tail test is being run.

Figure 15.2: Illustration of the \(Z\)-test, depicting the observed statistic (solid line), area for the \(p\)-values (shaded areas), and locations of the critical value (dotted lines). In this example, the critical value is at \(1.96\), and the observed statistic is at \(-2.473\). Thus, it falls outside of the critical value. Additionally, the shaded area gives the p-value, \(0.013\), which is less than the implied significance level of \(0.05\). Consider where the critical values would fall had \(\alpha = 0.01\) been used instead.

\(Z\)-Tests for Population Means in Normal Populations with Known Variances

If data are selected from a normal population, with a known variance, then the \(Z\)-test is the most common test to apply for hypotheses surrounding the population mean. Specifically, the test statistic is \[T = \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}},\] where \(\mu_0\) is the value of the mean under the null hypothesis. Then, supposing \(T=t\) is observed:

1. If \(H_0: \mu = \mu_0\) versus \(H_A: \mu \neq \mu_0\), the \(p\)-value is \(2\Phi(-|t|) = 2(1 - \Phi(|t|))\). The corresponding critical value is \(Z_{1-\alpha/2}\).
2. If \(H_0: \mu \geq \mu_0\) versus \(H_A: \mu < \mu_0\), the \(p\)-value is \(\Phi(t)\). The corresponding critical value is \(Z_{\alpha}\).
3. If \(H_0: \mu \leq \mu_0\) versus \(H_A: \mu > \mu_0\), the \(p\)-value is \(1 - \Phi(t)\). The corresponding critical value is \(Z_{1-\alpha}\).

15.3.2 One Sample \(t\)-Tests for Population Means

Suppose instead that we are dealing with a population with an unknown variance, but we are still only interested in the mean of the population. If the population is either normally distributed, or else if the sample size is large enough to justify the use of the Central Limit Theorem, then we know that \(\overline{X} \sim N(\mu, \sigma^2)\), however, \(\sigma^2\) is unknown. We have seen that we can replace \(\sigma\) with \(s\), the sample standard deviation, and update the corresponding sampling distribution to a \(t_{n-1}\). This result suggests that we run a \(t\)-test, taking \[T = \frac{\overline{X} - \mu_0}{s/\sqrt{n}} \stackrel{H_0}{\sim} t_{n-1}.\] Suppose that we observe \(T=t\), then owing to symmetry we can compute the relevant \(p\)-value as \[P(T \leq -|t|) + P(T \geq |t|) = 2F(-|t|),\] where \(F(t)\) is the cumulative distribution function for the \(t_{n-1}\) distribution. If instead we wish to use the critical value method, then we would need to solve \[2F(-t^*) = \alpha \iff t^* = t_{n-1, 1-\alpha/2},\] where \(t_{n-1,1-\alpha/2}\) is the critical value from the \(t_{n-1}\) distribution. If instead a one-tailed hypothesis test were run, we would take the \(p\)-value to be \(F(t)\) (or \(1-F(t)\)), and the critical value as either \(t_{n-1, \alpha}\) or \(t_{n-1, 1-\alpha}\).

Figure 15.3: Illustration of the \(t\)-test, based on \(n=32\), depicting the observed statistic (solid line), area for the \(p\)-values (shaded areas), and locations of the critical value (dotted lines). In this example, the critical value is at \(2.04\), and the observed statistic is at \(1.81\). Thus, it falls inside of the critical value. Additionally, the shaded area gives the p-value, \(0.080\), which is greater than the implied significance level of \(0.05\). Consider where the critical values would fall had a one-tailed hypothesis test been used instead.

\(t\)-Tests for Population Means in Normal Populations or Large Samples

If data are selected from a normal population, or from a non-normal population with a sufficiently large sample size, with an unknown variance, then the \(t\)-test is the most common test to apply for hypotheses surrounding the population mean. Specifically, the test statistic is \[T = \frac{\overline{X} - \mu_0}{s/\sqrt{n}},\] where \(\mu_0\) is the value of the mean under the null hypothesis. Define the sample size to be \(n\). Then, supposing \(T=t\) is observed, and taking \(F(t)\) to be the cumulative distribution function for the \(t_{n-1}\) distribution:

1. If \(H_0: \mu = \mu_0\) versus \(H_A: \mu \neq \mu_0\), the \(p\)-value is \(2F(-|t|) = 2(1 - F(|t|))\). The corresponding critical value is \(t_{n-1, 1-\alpha/2}\).
2. If \(H_0: \mu \geq \mu_0\) versus \(H_A: \mu < \mu_0\), the \(p\)-value is \(F(t)\). The corresponding critical value is \(t_{n-1, \alpha}\).
3. If \(H_0: \mu \leq \mu_0\) versus \(H_A: \mu > \mu_0\), the \(p\)-value is \(1 - F(t)\). The corresponding critical value is \(t_{n-1, 1-\alpha}\).

15.3.3 Hypothesis Tests for Population Proportions

Suppose that instead of concern with a population mean, we are instead concerned with a population proportion. We can either view the data as coming from a sample of \(n\) independent and identically distributed Bernoulli random variables, with success probability \(p\), or, equivalently, we can view these data as a single realization from a \(\text{Bin}(n, p)\) distribution. In the first case, take \[\widehat{p} = \frac{1}{n}\sum_{i=1}^n X_i = \overline{X},\] and so through the Central Limit Theorem, as long as \(n\) is sufficiently large, \(\widehat{p}\) will be approximately normal.¹² At this point, supposing we are testing a hypothesis of \(p\) as it relates to \(p_0\), then under the null \(\widehat{p} \sim N(p_0, p_0(1-p_0)/n)\). As such, \[T = \frac{\widehat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \stackrel{H_0}{\sim} N(0, 1).\] Correspondingly, we can apply a \(Z\)-test for the population proportions, following exactly the same procedure outlined above.

Note that in the case of a population proportion, the specification of the proportion under the null hypothesis also specifies the population variance. This is because, in a Bernoulli distribution, the mean and variance are governed by a single parameter. This means that we need not estimate the variance from the sample, nor consider the \(t\) distribution. If the null hypothesis holds, then the population mean will be exactly \(p_0\) and the variance \(p_0(1-p_0)/n\). However, this is still an approximate hypothesis test since it relies on the use of the Central Limit Theorem to justify normality.

15.4 Further Considerations of Hypothesis Testing

The process of hypothesis testing is used extensively across a wide variety of scenarios. It is quite flexible, and can accommodate any types of data or any hypotheses of interest, so long as a suitable test statistic and null distribution can be derived. With that said, hypothesis testing is not a panacea for scientific inquiry. It needs to be carefully and critically applied, informed by the context of the situation and driven by our underlying subject-matter expertise. We saw the importance of this when informing the hypothesis to test, whether to use a one-sided or two-sided alternative, and in selecting a threshold for the level of significance. At every stage of the process care is required in order to ensure that the results of our hypothesis tests are useful and valid.

15.4.1 Practical Significance versus Statistical Significance

A key consideration in the application of hypothesis testing is differentiating between those results that are statistically significant¹³ and those results that are practically significant. Practical significance, broadly speaking, indicates whether a particular effect actually matters given the underlying context.

Definition 15.16 (Practical Significance) A result is said to be practically significant if the effect is large enough to be meaningful in the real-world. Practical significance is not achieved on the basis of statistical analyses, but rather, on the basis of the subject-matter expertise. The degree of practical significance is somewhat subjective, and will depend on the particular context.

To assess practical significance in practice we should ask ourselves, supposing that the observed effects are real, do we even care? Consider a lifestyle intervention that, in medical studies, is found to increase an individual’s life expectancy by \(1\) day. This result may or may not be statistically significant, depending on the degree of evidence in the observed sample. However, this result is almost certainly not practically significant. That is because, even if it were found to be a strong statistical result, it is likely not a result that is large enough to care about it in practice. On the other hand, a lifestyle intervention that increases life expectancy by \(10\) years is likely to be very practically significant.

A result is only meaningful if it achieves both statistical significance and practical significance. Without statistical significance, we do not have strong enough evidence to believe that the observed result is really different from our null hypothesis. Without practical significance, we do not care about the existence of the result broadly. The combined statistical and practical significance means that, not only is there good evidence for the result, but there is also value in considering the result.

Critically, the degree of statistical significance is not a measure of practical significance. That is, a smaller \(p\)-value does not necessarily mean that the result is more practically significant. The measure of statistical significance is orthogonal to the measure of practical significance. Instead, to assess practical significance, we consider the size of the effect directly. The measure of effect size will be dependent on the given scenario and the specific parameter that is being assessed. This should be measured relative to known information in the field. Thus, if we are interested in the mean result, perhaps the effect size is given by the mean difference between the sample mean and the value under the null hypothesis. If we are interested in a proportion, we may take the absolute size of the proportion to measure the effect. Whatever value we can compare to our existing experience will serve as a basis for assessing the degree of practical significance that has been attained.

15.4.2 The Connection Between Hypothesis Testing and Confidence Levels

In discussing hypothesis testing we reintroduced many of the same concepts that were introduced during our discussions of confidence intervals as well. This is not coincidental, and it is not merely an aesthetic similarity. There is a fundamental connection between confidence intervals and hypothesis testing, one that renders them to be equivalent, in a sense, mathematically. More concretely, a confidence interval and a hypothesis test that are based on the same underlying statistic will always agree with one another.

Suppose that a hypothesis test is run, testing \(H_0: \theta = \theta_0\), and the computed \(p\)-value is \(0.01\). This means that, assuming that the null hypothesis is true, there is a probability of \(0.01\) that we would observe a result as extreme as the one we actually did. Now, recall that a confidence interval gives a range of values that, prior to actually conducting the sample, achieves some set probability of containing the true value. Suppose we construct a \(95\%\) confidence interval. This interval will have a probability of \(0.95\) of containing the truth, or put differently, there is a probability of \(0.05\) that the truth does not fall inside this interval. If we construct the interval on the same data for which we found a \(p\)-value of \(0.01\), where should we expect \(\theta_0\) to fall relative to our interval? The probability, assuming \(\theta = \theta_0\), that we observe a statistic as extreme as we did is \(0.01\). This is notably smaller than the \(0.05\) probability that the truth would fall outside the interval, and as such, we should not expect to see \(\theta_0\) in the interval.

Concretely, if a \(100(1-\alpha)\%\) confidence interval is formed, and it contains the null value \(\theta_0\), then the \(p\)-value for a hypothesis test of \(H_0: \theta = \theta_0\) will have a \(p\)-value that is greater than or equal to \(\alpha\). If the \(100(1-\alpha)\%\) confidence interval is formed and does not contain the null value \(\theta_0\), then the \(p\)-value for the hypothesis test will be less than \(\alpha\). Equivalently, if the \(p\)-value when testing \(H_0: \theta = \theta_0\) is found to be \(\alpha\), then every confidence interval that is at least as wide as \(100(1-\alpha)\%\) will contain \(\theta_0\), and every interval that is more narrow than this will not contain the null value.

One way to conceptualize this more concretely is to consider that a confidence interval is effectively giving you the set of values that, based on your sample, you have no evidence to differentiate between. Any value in your confidence interval is justified by the sample in being considered the true value. This justification stems from the fact that, prior to the construction of the interval, there was only an \(\alpha\) probability that the true value would not be in the interval, and so the values in this interval remain plausible based on the evidence. In a hypothesis test, we are trying to assess whether our sample contradicts a particular value for the truth, at a given threshold for evidence. If the value we are trying to reject is contained within our confidence interval, the logic of the confidence interval suggests that we should not reject it as possible. On the other hand, if the value we are interested in falls outside the confidence interval, our sample seems to reject its plausibility.

15.4.3 Critiques of Null Hypothesis Significance Testing

Despite the prevalence of hypothesis testing and the seemingly intuitive derivation of the procedure it is not without its faults, and it is not free of detractors. There are many critiques of hypothesis testing that are valid, and that should be seriously considered before an uncritical application of the procedures. The critiques of hypothesis tests tend to fall into two categories: there are the critiques about the application of hypothesis testing in practice, and there are critiques about the underlying foundation of hypothesis testing. The first can be remedied through careful application of the procedures we have discussed. The second represents a more philosophical debate, one in which competing sources of evidence need to be weighed against one another. Statisticians who are particularly critical of hypothesis testing, as it has been outlined here, often propose alternative procedures to accomplish similar goals. These frameworks are often rooted in fundamentally different approaches to the understanding of uncertainty, such as those emerging from the Bayesian paradigm. Such approaches to scientific knowledge and inquiry can be quite useful, but will not be pursued further in these notes.

While there are many critiques of hypothesis testing, we focus on four foundational concerns.

1. Effects are (basically) never truly zero. Most of the time, hypothesis testing is set up with a null hypothesis of \(H_0: \theta = 0\). This typically refers to the effect of some intervention (such as a medical treatment), or the difference in outcomes achieved after making some change, or similar. The hypothesis test then seeks to determine, based on the observed evidence, is the effect of interest really different from zero. Many individuals critique this framing since, in practice, we should not expect any effect to be exactly zero. Every factor likely exerts some influence, no matter how small, on any related factors. It may not be practically significant in terms of its effect size, but the only quantities that will truly have no effect on each other are quantities that are not likely to be tested against one another. As a result, for many hypothesis tests, the framework is set up to disprove a statement that no one actually believes. We are not seeking evidence of effect size, just that it is different from zero, but likely we should approach every situation expecting the effects to be different from zero.
2. In hypothesis testing, \(p\)-values are prioritized above all else. \(p\)-values are, at their core, a statistic computed based on a particular sample that provide a measure of the level of evidence against a null hypothesis. This is a continuous measure of evidence, with any value \((0,1)\) being theoretically possible. The process of hypothesis testing takes this continuous measure and expresses it discretely as either “statistically significant” or else “not statistically significant”, treating this discretization as the sole arbiter of whether an effect is real or not. Not only is there information lost by moving from a continuous measure to a discrete one based on only two categories, but this process also ignores other important sources of information that should likely be considered alongside a \(p\)-value. For instance, alongside a \(p\)-value we may wish to consider whatever prior evidence of the claim we may have, the scientific validity or plausibility of the underlying finding, the quality of the data or the study, the practical significance, and so forth. The critique in this context is not so much that \(p\)-values are not useful, but rather, that a sole reliance on \(p\)-values ignores many important factors.
3. The null hypothesis is often a straw man. This is related to the first point, but is more broad than the idea that we can typically assume that effects are non-zero. Recall that the null hypothesis is meant to be the default belief about the world, the state of affairs that we ought to believe without sufficient evidence contradicting it. A null hypothesis that actually satisfies this criterion is required for the utility of the hypothesis testing framework. Often, however, the null hypothesis that is selected is one that effectively no one would actually believe. This is a straw man.¹⁴ If the null hypothesis is not truly believed by anyone, or if it is so unlikely as to be irrelevant, then refuting it with a hypothesis test tells us nothing. At the heart of the hypothesis testing framework is the concept of falsification. We are not looking for positive, confirmatory support in favour of a particular hypothesis, but rather looking to falsify the null hypothesis. If the idea that we are falsifying is not particularly relevant, then the fact that we have falsified it is also not particularly relevant. Unfortunately, in practice, irrelevant null hypotheses are often used.
4. The hypothesis testing framework is ripe for abuse. In any statistical analysis there are many choices that need to be made by individuals conducting the analysis. Often, there are many reasonable sounding choices that could lead to valid results, if those choices are guided by substantive considerations. Different choices which may be reasonable in different settings can, if applied to the same analysis, lead to very different conclusions. This is a reality in any statistical analysis, but is particularly concerning in the hypothesis testing framework where there is often a single goal for the researcher, namely, find a result that is statistically significant. A researcher that is setting out to achieve statistical significance at all costs is able to make many choices that aid in this attempt, if so desired. This process, known as p-hacking, can be intentional or unintentional, and can involve decisions that are reasonable from the outside or decisions that are explicitly fraudulent. For instance, an investigator may consider using a one-sided hypothesis test, a choice that, while reasonable in some settings, has the effect of halving the observed \(p\)-value. Researchers may throw out certain data that they deem to be outliers because they do not follow the underlying trend they are looking for. Researchers may perform many different analyses, and only report those that happened to be statistically significant.¹⁵ The arbitrary nature of the level of significance is another area of choice for the researchers – if they calculate a \(p\)-value and find it to be \(0.08\), taking \(\alpha = 0.1\) allows them to report a statistically significant effect. The sum total of these choices means that any particular analysis, even if well-intentioned, may be subject to an artificially deflated \(p\)-value, achieving the moniker of statistical significance unfairly.

These critiques are not just theoretical. There has been, in recent years, major concern over the replicability of research in a wide range of fields. While there are many aspects that drive this so-called replication crisis, the inappropriate use of hypothesis testing is certainly among the explanations. In light of these critiques, it is worth questioning whether the framework of hypothesis testing is worthy of pursuit. Generally, it is reasonable to answer this with a cautious “yes”. However, it is critically important to take seriously these criticisms. Hypothesis testing should not be used to the exclusion of other forms of evidence. The hypothesis tests should not be dichotomized as “significant” or “not significant” where all results that are “significant” are treated as gospel and those that are “not significant” are treated as false. The selected null hypothesis should be a genuine null hypothesis, and the choices made in the analysis should be made prior to collecting or analyzing data on the basis of the context of the situation, rather than on the basis of what happens to be observed. Hypothesis testing should be used to support scientific inquiry, not as the sole tool of scientific inquiry. In short, the process of hypothesis testing provides a useful, statistical framework for assessing the degree of evidence that exists within a sample, however, it should never be applied uncritically.

15.5 Hypothesis Testing in R

Hypothesis testing in R can proceed in one of two ways. First, test statistics can be directly computed, and then functions (such as pnorm or similar) can be used to compute \(p\)-values according to the null distribution. Alternatively, many common hypothesis tests are built into R to begin. The most relevant function, given the tests that were discussed throughout this chapter, is the t.test function. This will perform a \(t\)-test, based on a sample of data, contrasting the mean against a particular value. Moreover, the t.test function will, by default, produce confidence intervals for the mean, allowing both to be reported alongside one another. If you wish to perform a hypothesis test that is not built-in, then this can be accomplished using the same procedures outlined for confidence intervals.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 15.1

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0368189968)

\(\sigma_1^2 - \sigma_2^2 \geq -21\)\(S_X^2 - S_Y^2 = -22\)\(\sigma_1^2 - \sigma_2^2 \neq 37\)\(\theta \geq -64\).\(\theta_1 - \theta_2 \geq -95\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0005858495)

\(\overline{X} \neq -93\).\(\theta < -87\).\(\mu_1 < \mu_2\)\(\mu_1 - \mu_2 < -47\)\(\theta \neq 73\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0973478387)

\(S_X = S_Y\)\(X - Y \neq -17\)\(\mu_1 \neq \mu_2\)\(S_X > S_Y\)\(X \leq -85\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0870521544)

\(\sigma_1 > \sigma_2\)\(\sigma \neq 49\).\(\sigma^2 > 11\).\(\sigma > 41\).\(\overline{X} = 87\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0439450882)

\(\mu_1 - \mu_2 \neq 12\)\(S_X^2 < 61\).\(\sigma_1 - \sigma_2 = 1\)\(\mu \leq -58\).\(\theta_1 \geq \theta_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0735235852)

\(\sigma_1^2 \geq \sigma_2^2\)\(\mu < -24\).\(\mu = 11\).\(X > Y\)\(\theta_1 \geq \theta_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0462769893)

\(\sigma_1^2 = \sigma_2^2\)\(\overline{X} \neq \overline{Y}\)\(\sigma_1 \leq \sigma_2\)\(\sigma_1^2 > \sigma_2^2\)\(\mu_1 \neq \mu_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0395669627)

\(\mu \geq 51\).\(\theta_1 \geq \theta_2\)\(\theta_1 - \theta_2 \neq -95\)\(\overline{X} - \overline{Y} < 54\)\(\sigma_1^2 - \sigma_2^2 \neq 42\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0264964642)

\(S_X > 82\).\(S_X < S_Y\)\(X = 65\).\(\sigma_1 > \sigma_2\)\(X - Y \leq -98\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0192074064)

\(\overline{X} - \overline{Y} \neq -15\)\(S_X^2 - S_Y^2 \neq -44\)\(X \geq Y\)\(\overline{X} \neq -58\).\(\sigma_1^2 < \sigma_2^2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0628893088)

\(\sigma_1^2 = \sigma_2^2\)\(\theta_1 = \theta_2\)\(X \neq 42\).\(\theta_1 - \theta_2 < -99\)\(\mu \geq -22\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0863817935)

\(\mu \geq -70\).\(\sigma \neq 96\).\(\sigma^2 \geq 17\).\(\mu < -3\).\(S_X^2 - S_Y^2 \geq 61\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0187121802)

\(\theta_1 - \theta_2 \neq -34\)\(S_X^2 - S_Y^2 < -11\)\(\overline{X} \leq \overline{Y}\)\(X - Y \leq -22\)\(X < -32\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0082819283)

\(\theta_1 - \theta_2 \neq 8\)\(S_X - S_Y > -20\)\(\overline{X} - \overline{Y} \leq -35\)\(S_X \leq 69\).\(S_X - S_Y \geq 73\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0547017503)

\(\sigma_1 \neq \sigma_2\)\(\theta_1 > \theta_2\)\(\mu \leq -1\).\(\theta_1 \geq \theta_2\)\(S_X^2 \leq S_Y^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0526763720)

\(S_X^2 - S_Y^2 > 38\)\(\sigma < 68\).\(S_X^2 > S_Y^2\)\(S_X - S_Y < -48\)\(X - Y \leq 56\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0747503340)

\(\sigma_1 - \sigma_2 \geq 55\)\(\sigma_1^2 - \sigma_2^2 \leq 79\)\(\sigma_1^2 - \sigma_2^2 = -29\)\(S_X^2 = 75\).\(\sigma_1^2 \neq \sigma_2^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0558494348)

\(S_X^2 = 78\).\(S_X \leq 33\).\(S_X - S_Y = -66\)\(\overline{X} = \overline{Y}\)\(\theta_1 - \theta_2 \leq -64\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0914438944)

\(S_X - S_Y < 1\)\(\theta_1 - \theta_2 \geq 54\)\(X > Y\)\(\overline{X} - \overline{Y} < -57\)\(S_X^2 \neq 59\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0964134720)

\(S_X^2 - S_Y^2 \geq -9\)\(S_X \leq S_Y\)\(\overline{X} \neq \overline{Y}\)\(\sigma_1 - \sigma_2 \neq -11\)\(S_X < S_Y\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0780333401)

\(S_X^2 - S_Y^2 < 59\)\(\theta > -24\).\(\sigma_1 - \sigma_2 > -93\)\(\mu_1 - \mu_2 \neq -80\)\(\theta_1 \geq \theta_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0124711488)

\(\theta_1 - \theta_2 > 30\)\(\sigma_1 \geq \sigma_2\)\(\sigma_1^2 - \sigma_2^2 = 30\)\(\overline{X} - \overline{Y} = 12\)\(\sigma^2 = 10\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0239064518)

\(\sigma^2 \geq 51\).\(X \geq -27\).\(\sigma_1^2 - \sigma_2^2 \neq 46\)\(\sigma_1^2 \leq \sigma_2^2\)\(\mu_1 - \mu_2 > 0\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0881241900)

\(S_X \neq 25\).\(\sigma_1 > \sigma_2\)\(\sigma < 40\).\(\mu_1 - \mu_2 < -39\)\(\mu \leq 31\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0932907631)

\(\mu_1 - \mu_2 > 96\)\(\sigma_1 = \sigma_2\)\(\theta = -30\).\(X < -23\).\(\mu_1 - \mu_2 \leq 56\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0339577400)

\(\sigma_1 \neq \sigma_2\)\(\mu_1 - \mu_2 \leq -1\)\(\mu_1 - \mu_2 > 77\)\(\theta \geq -29\).\(S_X - S_Y > 3\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0994824707)

\(\sigma_1 - \sigma_2 \geq 35\)\(\theta_1 \neq \theta_2\)\(\mu > -8\).\(S_X - S_Y = -3\)\(\theta < -55\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0624369714)

\(\theta_1 = \theta_2\)\(\theta < 60\).\(\sigma_1 \geq \sigma_2\)\(\mu_1 \geq \mu_2\)\(\overline{X} - \overline{Y} \geq 85\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0474952201)

\(\overline{X} - \overline{Y} \leq 87\)\(\sigma^2 \neq 43\).\(\sigma = 87\).\(\sigma_1 \geq \sigma_2\)\(\theta < 45\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0934489917)

\(X \geq 0\).\(S_X^2 \neq S_Y^2\)\(X \leq 87\).\(\sigma_1^2 < \sigma_2^2\)\(S_X > 7\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0259356825)

\(S_X \neq 95\).\(\mu \neq -34\).\(\sigma_1^2 - \sigma_2^2 > -79\)\(\theta \neq -22\).\(\theta_1 \neq \theta_2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0911907284)

\(S_X \neq 93\).\(\sigma_1 = \sigma_2\)\(\overline{X} \neq 22\).\(\overline{X} \geq 11\).\(S_X - S_Y \geq 67\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0581636270)

\(\sigma > 27\).\(S_X - S_Y \geq -94\)\(S_X^2 = S_Y^2\)\(S_X = S_Y\)\(S_X^2 > S_Y^2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0416011634)

\(\mu > -39\).\(\sigma^2 = 2\).\(\theta_1 - \theta_2 \neq 33\)\(\sigma_1^2 \geq \sigma_2^2\)\(S_X^2 \neq S_Y^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0267810756)

\(S_X - S_Y \leq 3\)\(X - Y \neq -6\)\(\overline{X} \neq \overline{Y}\)\(X - Y > -64\)\(\mu_1 \neq \mu_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0019761277)

\(\sigma_1 - \sigma_2 \leq -37\)\(\theta > -73\).\(\sigma_1^2 - \sigma_2^2 \geq 87\)\(\mu > 98\).\(X \neq 16\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0383024121)

\(S_X^2 - S_Y^2 \leq 48\)\(S_X - S_Y \leq 79\)\(\mu_1 \geq \mu_2\)\(X \neq -45\).\(X - Y \leq -50\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0420436483)

\(\mu_1 \geq \mu_2\)\(\sigma_1^2 = \sigma_2^2\)\(S_X = S_Y\)\(\sigma^2 > 72\).\(\sigma = 30\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0105053579)

\(\sigma_1 - \sigma_2 > 31\)\(\mu_1 - \mu_2 \neq -44\)\(\sigma^2 > 36\).\(\overline{X} \leq -13\).\(\sigma_1^2 \geq \sigma_2^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0743780485)

\(S_X - S_Y > 51\)\(S_X^2 - S_Y^2 < -78\)\(\theta \neq 15\).\(X - Y \neq 14\)\(X \neq Y\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0169458329)

\(\mu_1 \geq \mu_2\)\(\sigma_1^2 - \sigma_2^2 = 84\)\(\sigma \geq 50\).\(X \leq Y\)\(\mu_1 - \mu_2 \neq -69\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0104476664)

\(\sigma_1^2 - \sigma_2^2 \leq -75\)\(S_X^2 = S_Y^2\)\(S_X^2 < S_Y^2\)\(X \neq Y\)\(X - Y > 5\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0199907222)

\(\sigma_1 - \sigma_2 \neq -49\)\(\sigma_1 > \sigma_2\)\(\sigma_1^2 \geq \sigma_2^2\)\(S_X^2 > S_Y^2\)\(\sigma_1^2 - \sigma_2^2 \neq 66\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0424749082)

\(\mu_1 - \mu_2 \neq -27\)\(\mu = -89\).\(\theta_1 - \theta_2 < -12\)\(\mu > 5\).\(X = -41\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0846287693)

\(X \leq Y\)\(\sigma_1^2 - \sigma_2^2 = 19\)\(X - Y > 89\)\(\overline{X} \neq -55\).\(\overline{X} - \overline{Y} = -87\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0543681850)

\(\theta_1 \geq \theta_2\)\(\overline{X} - \overline{Y} \neq -4\)\(\theta_1 - \theta_2 < 76\)\(\sigma_1 < \sigma_2\)\(\sigma^2 > 100\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0675276441)

\(\sigma_1^2 - \sigma_2^2 > -62\)\(\overline{X} < \overline{Y}\)\(S_X \leq 53\).\(X - Y \geq -99\)\(S_X^2 > 29\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0421727362)

\(X - Y < -82\)\(S_X - S_Y = 93\)\(S_X \neq S_Y\)\(S_X - S_Y > -7\)\(\theta < -36\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0011772515)

\(\sigma^2 > 29\).\(\mu = 43\).\(\sigma_1^2 - \sigma_2^2 > 15\)\(\sigma = 72\).\(\overline{X} \neq \overline{Y}\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0064539557)

\(\mu \leq -49\).\(\sigma_1 \neq \sigma_2\)\(\sigma_1^2 \neq \sigma_2^2\)\(\overline{X} < -66\).\(\sigma_1^2 - \sigma_2^2 \leq -38\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0503493660)

\(\theta_1 \leq \theta_2\)\(\overline{X} \neq -19\).\(\mu = 65\).\(\sigma_1^2 - \sigma_2^2 < 60\)\(\sigma \geq 32\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0315519865)

\(\overline{X} - \overline{Y} < -72\)\(X \neq Y\)\(\mu_1 - \mu_2 \leq -86\)\(X < Y\)\(S_X < 1\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0268874712)

\(\mu_1 - \mu_2 \leq 14\)\(\overline{X} \neq 50\).\(X - Y \leq 100\)\(S_X^2 - S_Y^2 \leq 45\)\(S_X > 62\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0183720345)

\(\sigma_1^2 \leq \sigma_2^2\)\(\sigma_1 > \sigma_2\)\(\sigma_1^2 \neq \sigma_2^2\)\(\overline{X} > -83\).\(\mu_1 - \mu_2 \leq 24\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0155203522)

\(\mu_1 \geq \mu_2\)\(\overline{X} > \overline{Y}\)\(\mu_1 - \mu_2 \neq -95\)\(\mu_1 - \mu_2 \leq 74\)\(\mu \neq -22\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0712228205)

\(\overline{X} \neq -28\).\(S_X - S_Y \leq 22\)\(\overline{X} \geq \overline{Y}\)\(S_X^2 \geq S_Y^2\)\(\sigma_1 = \sigma_2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0985713270)

\(S_X < 72\).\(\mu_1 - \mu_2 > 2\)\(S_X^2 > 30\).\(S_X^2 - S_Y^2 > -47\)\(X < 22\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0069598409)

\(\theta_1 = \theta_2\)\(\sigma_1 - \sigma_2 \neq -72\)\(\theta > -37\).\(X < 56\).\(\theta_1 - \theta_2 \neq -41\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0838322509)

\(S_X^2 > S_Y^2\)\(\sigma < 96\).\(S_X = 39\).\(S_X^2 - S_Y^2 \geq -87\)\(\overline{X} - \overline{Y} = 94\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0032505664)

\(S_X - S_Y > 96\)\(\theta_1 = \theta_2\)\(\mu_1 - \mu_2 > 55\)\(\mu_1 < \mu_2\)\(\sigma \geq 51\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0131944649)

\(\mu_1 - \mu_2 \leq 17\)\(\overline{X} = \overline{Y}\)\(S_X - S_Y > 88\)\(X = Y\)\(\overline{X} - \overline{Y} \neq 90\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0649609565)

\(\mu_1 - \mu_2 \neq -40\)\(\sigma \neq 16\).\(\sigma_1 < \sigma_2\)\(S_X^2 \leq 78\).\(\theta_1 - \theta_2 \leq -11\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0496019866)

\(\mu_1 > \mu_2\)\(X - Y \geq -47\)\(S_X > S_Y\)\(S_X^2 \leq 5\).\(X \neq -88\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0005561962)

\(\theta_1 - \theta_2 \neq -29\)\(\theta_1 \geq \theta_2\)\(S_X \neq 46\).\(\sigma \geq 72\).\(\mu_1 - \mu_2 = 0\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0047769612)

\(\sigma_1^2 \neq \sigma_2^2\)\(\overline{X} \geq \overline{Y}\)\(\mu_1 < \mu_2\)\(\sigma_1 - \sigma_2 < 1\)\(\sigma^2 < 79\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0873154500)

\(\sigma_1 < \sigma_2\)\(\sigma^2 > 42\).\(\theta_1 - \theta_2 \geq 22\)\(\overline{X} \neq \overline{Y}\)\(\mu_1 \leq \mu_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0918814781)

\(\sigma_1^2 > \sigma_2^2\)\(S_X^2 \geq 63\).\(\theta_1 < \theta_2\)\(\sigma_1^2 - \sigma_2^2 < -36\)\(\sigma \geq 83\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0364726585)

\(X - Y > -98\)\(S_X^2 = 76\).\(S_X^2 - S_Y^2 \leq 63\)\(\mu_1 - \mu_2 > -54\)\(S_X \neq 90\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0675049476)

\(\overline{X} = \overline{Y}\)\(S_X < S_Y\)\(\overline{X} \leq \overline{Y}\)\(\sigma^2 > 86\).\(\overline{X} = 13\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0758089803)

\(\sigma^2 = 84\).\(\mu_1 - \mu_2 \leq -45\)\(S_X^2 - S_Y^2 = 13\)\(\mu_1 - \mu_2 \neq 34\)\(\sigma \geq 95\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0604960797)

\(\mu = -73\).\(S_X^2 > S_Y^2\)\(S_X^2 \neq 31\).\(\overline{X} = \overline{Y}\)\(X < 69\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0002619668)

\(\sigma_1^2 - \sigma_2^2 \leq 2\)\(\theta_1 - \theta_2 \geq 37\)\(\theta_1 \neq \theta_2\)\(\sigma \geq 9\).\(X - Y \leq 38\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0077564911)

\(S_X^2 \neq S_Y^2\)\(S_X \leq S_Y\)\(\overline{X} \leq \overline{Y}\)\(S_X \neq S_Y\)\(\mu < -6\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0348026465)

\(X < Y\)\(\mu_1 - \mu_2 \neq 66\)\(S_X - S_Y > 52\)\(X - Y \leq -96\)\(S_X^2 > S_Y^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0429130313)

\(S_X < S_Y\)\(\sigma_1 \neq \sigma_2\)\(S_X^2 > 17\).\(X - Y \leq -51\)\(S_X^2 - S_Y^2 \leq 68\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0916442196)

\(\sigma^2 \geq 67\).\(\sigma_1 - \sigma_2 = 64\)\(S_X - S_Y > -60\)\(\theta > -53\).\(\mu_1 \leq \mu_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0984261358)

\(S_X \geq S_Y\)\(\sigma < 15\).\(\theta < -21\).\(\sigma^2 = 18\).\(\sigma_1^2 \geq \sigma_2^2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0435059034)

\(X < 64\).\(S_X \neq 23\).\(S_X^2 = 27\).\(\theta_1 - \theta_2 < -43\)\(X \neq -11\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0184952384)

\(\mu_1 - \mu_2 \neq -35\)\(S_X \geq S_Y\)\(\overline{X} - \overline{Y} \leq -81\)\(S_X^2 = S_Y^2\)\(S_X \leq S_Y\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0636827390)

\(\overline{X} < -28\).\(S_X^2 - S_Y^2 > 64\)\(X \geq -47\).\(\sigma_1^2 - \sigma_2^2 = -58\)\(S_X^2 - S_Y^2 < -23\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0185855224)

\(\theta_1 = \theta_2\)\(\sigma_1 < \sigma_2\)\(X < Y\)\(\sigma \geq 5\).\(\theta_1 - \theta_2 = -41\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0706906616)

\(X - Y = -42\)\(\mu_1 - \mu_2 \neq 83\)\(\theta_1 \geq \theta_2\)\(\sigma_1 - \sigma_2 \geq 53\)\(\mu_1 = \mu_2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0576296157)

\(X > Y\)\(X \neq 3\).\(\overline{X} - \overline{Y} > 75\)\(S_X - S_Y \geq -75\)\(\mu_1 > \mu_2\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0857182182)

\(\theta_1 - \theta_2 \geq 51\)\(\sigma_1 = \sigma_2\)\(\sigma > 5\).\(\mu_1 \leq \mu_2\)\(\overline{X} \leq \overline{Y}\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0577130437)

\(\mu_1 - \mu_2 \geq 27\)\(\theta_1 - \theta_2 \neq -63\)\(\mu \leq -25\).\(\mu_1 \geq \mu_2\)\(S_X \leq S_Y\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0527911760)

\(\sigma_1^2 = \sigma_2^2\)\(\theta_1 - \theta_2 > 31\)\(\theta < -12\).\(\overline{X} \leq \overline{Y}\)\(\mu_1 - \mu_2 < -92\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0012975382)

\(S_X^2 = S_Y^2\)\(S_X - S_Y \neq -97\)\(\mu_1 = \mu_2\)\(S_X^2 \leq S_Y^2\)\(X - Y \leq 90\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0765219722)

\(X > Y\)\(S_X^2 - S_Y^2 \neq 64\)\(S_X^2 - S_Y^2 \geq -97\)\(S_X < S_Y\)\(\sigma_1^2 - \sigma_2^2 < -3\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0317093011)

\(\mu \geq 8\).\(\overline{X} = \overline{Y}\)\(\theta_1 - \theta_2 \neq 23\)\(\theta_1 = \theta_2\)\(\sigma < 67\).

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0872857625)

\(\mu_1 = \mu_2\)\(\overline{X} > \overline{Y}\)\(\sigma_1 > \sigma_2\)\(\sigma_1 - \sigma_2 \leq -18\)\(\mu_1 > \mu_2\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0934387990)

\(S_X^2 = S_Y^2\)\(S_X < S_Y\)\(\sigma_1^2 \geq \sigma_2^2\)\(S_X - S_Y = 0\)\(X < -84\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0424252664)

\(S_X = 83\).\(\sigma_1 \geq \sigma_2\)\(\overline{X} < -16\).\(S_X^2 - S_Y^2 \leq 58\)\(X - Y \geq -98\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0964573231)

\(\sigma_1^2 - \sigma_2^2 = -91\)\(\mu_1 - \mu_2 > 21\)\(\theta = 68\).\(\mu_1 \leq \mu_2\)\(\overline{X} = \overline{Y}\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0741044074)

\(\sigma_1^2 = \sigma_2^2\)\(X < Y\)\(S_X \geq 22\).\(S_X^2 \leq S_Y^2\)\(S_X < 61\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0265357855)

\(\overline{X} = 24\).\(\sigma_1^2 - \sigma_2^2 \geq 74\)\(\overline{X} \geq \overline{Y}\)\(\overline{X} < \overline{Y}\)\(S_X \geq S_Y\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0477763678)

\(S_X^2 \neq 54\).\(\theta \leq -69\).\(\sigma_1^2 \geq \sigma_2^2\)\(\theta_1 \leq \theta_2\)\(\mu_1 - \mu_2 \geq -12\)

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0752664791)

\(\theta_1 \leq \theta_2\)\(S_X^2 - S_Y^2 > -20\)\(X - Y > -22\)\(S_X^2 - S_Y^2 \neq 36\)\(S_X^2 - S_Y^2 \geq -61\)

Which of the following statements is not a valid statistical hypothesis?

(Question ID: 0750240496)

\(\sigma_1 - \sigma_2 > -35\)\(\sigma > 18\).\(\sigma_1^2 \neq \sigma_2^2\)\(X - Y \geq -19\)\(\sigma^2 \leq 73\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0009205430)

\(S_X^2 < 24\).\(\overline{X} - \overline{Y} < 26\)\(\theta_1 \neq \theta_2\)\(\overline{X} > \overline{Y}\)\(S_X \geq 60\).

Which of the following statements is a valid statistical hypothesis?

(Question ID: 0293452883)

\(S_X < 98\).\(\sigma_1^2 - \sigma_2^2 \leq 37\)\(X \leq Y\)\(\overline{X} \leq -77\).\(\overline{X} \neq 49\).

Self Assessment 15.2

Which of the following statements is a valid null hypothesis?

(Question ID: 0313677688)

\(\sigma^2 = 11\).\(\sigma_1 \neq \sigma_2\)\(\theta \neq -53\).\(\mu_1 < \mu_2\)\(\sigma^2 > 96\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0561340792)

\(\sigma_1 \leq \sigma_2\)\(\theta \leq 52\).\(\sigma < 18\).\(\mu_1 - \mu_2 = 26\)\(\theta \geq -87\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0465364096)

\(\theta = 14\).\(\mu_1 \neq \mu_2\)\(\sigma_1 - \sigma_2 < -72\)\(\theta < -1\).\(\sigma^2 < 83\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0223342424)

\(\sigma_1 \neq \sigma_2\)\(\mu_1 - \mu_2 < -50\)\(\mu_1 - \mu_2 \neq 94\)\(\sigma_1^2 = \sigma_2^2\)\(\sigma^2 > 97\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0662536287)

\(\mu_1 \geq \mu_2\)\(\theta_1 = \theta_2\)\(\mu < 53\).\(\sigma_1 - \sigma_2 \leq -48\)\(\mu_1 \leq \mu_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0017588891)

\(\mu_1 < \mu_2\)\(\theta_1 \neq \theta_2\)\(\sigma_1^2 > \sigma_2^2\)\(\theta > 15\).\(\mu \leq -33\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0452819152)

\(\mu_1 \leq \mu_2\)\(\mu_1 - \mu_2 \leq 19\)\(\mu < 42\).\(\theta_1 - \theta_2 = -1\)\(\sigma \geq 47\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0364534957)

\(\sigma < 89\).\(\theta > -100\).\(\sigma^2 < 16\).\(\sigma_1^2 > \sigma_2^2\)\(\theta \leq -63\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0075028892)

\(\theta_1 - \theta_2 \geq 14\)\(\sigma = 71\).\(\sigma_1^2 > \sigma_2^2\)\(\theta = 74\).\(\sigma^2 \geq 8\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0940331482)

\(\theta > 55\).\(\mu_1 - \mu_2 > 3\)\(\theta_1 > \theta_2\)\(\sigma_1 - \sigma_2 > -54\)\(\sigma_1 = \sigma_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0262055116)

\(\sigma \neq 86\).\(\sigma_1^2 > \sigma_2^2\)\(\mu_1 < \mu_2\)\(\sigma^2 = 69\).\(\mu_1 - \mu_2 < 61\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0520270341)

\(\sigma_1^2 - \sigma_2^2 = 44\)\(\sigma_1 < \sigma_2\)\(\theta \neq -94\).\(\theta < -76\).\(\theta_1 \neq \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0715888315)

\(\sigma_1^2 - \sigma_2^2 > -28\)\(\mu_1 - \mu_2 \leq 77\)\(\sigma_1^2 \neq \sigma_2^2\)\(\mu_1 > \mu_2\)\(\sigma_1 - \sigma_2 > 96\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0571411463)

\(\sigma_1 - \sigma_2 = 11\)\(\sigma_1 = \sigma_2\)\(\theta_1 < \theta_2\)\(\sigma_1 - \sigma_2 \leq 33\)\(\sigma^2 \leq 38\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0202088879)

\(\sigma_1 \leq \sigma_2\)\(\theta_1 - \theta_2 = 72\)\(\sigma_1^2 \neq \sigma_2^2\)\(\theta \leq 64\).\(\mu_1 \leq \mu_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0868563736)

\(\sigma_1^2 < \sigma_2^2\)\(\mu = 93\).\(\theta_1 = \theta_2\)\(\theta = 51\).\(\theta \geq -13\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0650818799)

\(\theta_1 \leq \theta_2\)\(\theta_1 = \theta_2\)\(\sigma_1^2 - \sigma_2^2 < 95\)\(\sigma_1 - \sigma_2 \leq -33\)\(\sigma \geq 1\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0669267853)

\(\theta_1 > \theta_2\)\(\mu \neq -71\).\(\sigma_1 - \sigma_2 < -52\)\(\sigma_1^2 - \sigma_2^2 \leq 15\)\(\sigma_1 < \sigma_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0651083768)

\(\theta_1 \neq \theta_2\)\(\mu_1 - \mu_2 = -93\)\(\sigma = 16\).\(\sigma_1^2 - \sigma_2^2 \leq 6\)\(\sigma_1 - \sigma_2 \leq 87\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0698397727)

\(\sigma_1 > \sigma_2\)\(\sigma_1^2 - \sigma_2^2 \leq 93\)\(\sigma \leq 66\).\(\mu_1 \leq \mu_2\)\(\mu_1 - \mu_2 = -35\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0916143678)

\(\mu_1 - \mu_2 > -78\)\(\sigma_1^2 < \sigma_2^2\)\(\sigma^2 = 88\).\(\sigma < 10\).\(\sigma^2 < 59\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0971708250)

\(\sigma_1^2 - \sigma_2^2 < -22\)\(\sigma_1^2 - \sigma_2^2 \leq 32\)\(\theta < -39\).\(\mu_1 \neq \mu_2\)\(\theta_1 - \theta_2 < 72\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0001754407)

\(\sigma_1^2 \leq \sigma_2^2\)\(\theta < 81\).\(\sigma \geq 79\).\(\sigma = 92\).\(\mu_1 - \mu_2 = 91\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0657103866)

\(\theta_1 \neq \theta_2\)\(\sigma_1 - \sigma_2 \neq -8\)\(\sigma > 6\).\(\theta \leq -57\).\(\theta_1 < \theta_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0445339562)

\(\sigma_1 - \sigma_2 \leq -69\)\(\sigma_1^2 > \sigma_2^2\)\(\theta = -71\).\(\sigma_1^2 \geq \sigma_2^2\)\(\sigma^2 \geq 3\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0380676560)

\(\theta_1 - \theta_2 = -14\)\(\mu_1 \geq \mu_2\)\(\sigma_1 - \sigma_2 = -31\)\(\mu_1 > \mu_2\)\(\theta_1 \leq \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0576134953)

\(\sigma_1^2 - \sigma_2^2 < -11\)\(\theta \neq 8\).\(\sigma_1 - \sigma_2 > -50\)\(\mu \leq 30\).\(\sigma^2 \neq 64\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0961798119)

\(\theta_1 \geq \theta_2\)\(\sigma_1^2 \geq \sigma_2^2\)\(\mu_1 = \mu_2\)\(\sigma_1 > \sigma_2\)\(\sigma_1 \leq \sigma_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0870999312)

\(\mu \neq -89\).\(\sigma^2 \neq 84\).\(\sigma_1^2 > \sigma_2^2\)\(\mu_1 - \mu_2 \leq -41\)\(\sigma_1^2 < \sigma_2^2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0815120292)

\(\sigma_1 < \sigma_2\)\(\theta > 98\).\(\sigma^2 \geq 46\).\(\theta_1 - \theta_2 > -14\)\(\sigma_1 \neq \sigma_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0211010990)

\(\sigma_1 - \sigma_2 \leq -54\)\(\sigma \leq 82\).\(\theta_1 - \theta_2 \geq -62\)\(\sigma_1^2 \neq \sigma_2^2\)\(\sigma_1^2 - \sigma_2^2 \geq 52\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0498093453)

\(\theta \neq -21\).\(\sigma_1^2 - \sigma_2^2 \leq 74\)\(\sigma_1^2 < \sigma_2^2\)\(\mu > -61\).\(\sigma_1 - \sigma_2 \neq -75\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0240763929)

\(\sigma = 36\).\(\sigma^2 \leq 68\).\(\sigma^2 \neq 60\).\(\theta_1 - \theta_2 \leq 60\)\(\mu \geq 8\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0240832062)

\(\sigma_1^2 \geq \sigma_2^2\)\(\mu_1 - \mu_2 < -65\)\(\mu_1 = \mu_2\)\(\theta \geq 44\).\(\theta_1 - \theta_2 \geq 99\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0857076776)

\(\theta_1 \geq \theta_2\)\(\sigma_1^2 - \sigma_2^2 \neq -35\)\(\mu \neq 24\).\(\sigma_1 - \sigma_2 \neq -32\)\(\mu_1 - \mu_2 < -37\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0414694441)

\(\theta \geq -8\).\(\mu_1 - \mu_2 \leq 50\)\(\sigma_1 - \sigma_2 \geq 28\)\(\mu > 64\).\(\sigma \geq 39\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0607339430)

\(\mu > 71\).\(\theta_1 \leq \theta_2\)\(\theta \neq 84\).\(\theta < -98\).\(\mu \neq -40\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0387286343)

\(\sigma^2 < 35\).\(\sigma^2 \geq 74\).\(\mu_1 - \mu_2 = -75\)\(\sigma_1 \geq \sigma_2\)\(\theta_1 = \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0071996975)

\(\mu_1 \geq \mu_2\)\(\theta > -91\).\(\sigma^2 > 33\).\(\theta_1 > \theta_2\)\(\theta \neq -98\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0335054130)

\(\mu_1 - \mu_2 \leq 49\)\(\sigma = 11\).\(\sigma^2 < 25\).\(\sigma_1^2 - \sigma_2^2 \leq -68\)\(\mu_1 - \mu_2 \geq -2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0739252701)

\(\sigma_1^2 \leq \sigma_2^2\)\(\sigma_1^2 > \sigma_2^2\)\(\sigma_1^2 = \sigma_2^2\)\(\mu_1 - \mu_2 \leq 6\)\(\theta_1 = \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0052716036)

\(\sigma_1^2 \neq \sigma_2^2\)\(\mu_1 < \mu_2\)\(\sigma_1^2 - \sigma_2^2 > -12\)\(\sigma_1^2 \geq \sigma_2^2\)\(\mu < 71\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0423853965)

\(\mu_1 - \mu_2 = 68\)\(\sigma_1 - \sigma_2 = -46\)\(\theta_1 - \theta_2 > 27\)\(\mu_1 = \mu_2\)\(\theta = -60\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0108990842)

\(\sigma^2 \geq 45\).\(\sigma_1 - \sigma_2 \neq 58\)\(\mu_1 - \mu_2 < 63\)\(\mu_1 < \mu_2\)\(\sigma^2 \neq 36\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0918453751)

\(\sigma_1 - \sigma_2 > -14\)\(\sigma_1^2 - \sigma_2^2 < 96\)\(\theta_1 > \theta_2\)\(\sigma_1^2 = \sigma_2^2\)\(\mu_1 - \mu_2 < 11\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0614619935)

\(\sigma \geq 21\).\(\sigma_1^2 - \sigma_2^2 > 94\)\(\sigma_1 \leq \sigma_2\)\(\sigma_1 \geq \sigma_2\)\(\mu_1 - \mu_2 = -64\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0624515445)

\(\theta \neq 22\).\(\sigma_1^2 - \sigma_2^2 > -32\)\(\sigma_1 - \sigma_2 > 61\)\(\sigma_1 - \sigma_2 \geq 57\)\(\sigma \neq 9\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0442348074)

\(\sigma_1^2 \geq \sigma_2^2\)\(\mu_1 \leq \mu_2\)\(\mu = 39\).\(\mu_1 = \mu_2\)\(\sigma^2 > 95\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0097858784)

\(\theta \leq -68\).\(\sigma_1^2 - \sigma_2^2 \geq 14\)\(\mu \leq 16\).\(\sigma_1 - \sigma_2 > -28\)\(\sigma^2 = 4\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0581492158)

\(\theta_1 \geq \theta_2\)\(\mu_1 = \mu_2\)\(\sigma_1^2 - \sigma_2^2 > 91\)\(\theta \leq -57\).\(\mu \leq -28\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0943741263)

\(\sigma_1^2 \geq \sigma_2^2\)\(\sigma^2 \geq 9\).\(\sigma_1 - \sigma_2 = -11\)\(\mu_1 > \mu_2\)\(\theta_1 \geq \theta_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0756415007)

\(\theta = 18\).\(\sigma < 21\).\(\mu_1 - \mu_2 \geq 57\)\(\sigma_1 = \sigma_2\)\(\sigma_1^2 - \sigma_2^2 \leq -64\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0014614345)

\(\theta \leq 64\).\(\mu_1 - \mu_2 \leq -28\)\(\sigma_1^2 - \sigma_2^2 = 16\)\(\sigma_1^2 - \sigma_2^2 > -96\)\(\theta_1 - \theta_2 \leq -31\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0884293779)

\(\mu_1 - \mu_2 > -95\)\(\theta < -38\).\(\sigma_1^2 < \sigma_2^2\)\(\sigma < 37\).\(\mu \leq -41\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0661416703)

\(\theta_1 > \theta_2\)\(\mu_1 > \mu_2\)\(\sigma_1^2 \neq \sigma_2^2\)\(\sigma^2 \neq 7\).\(\mu \geq -21\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0105023983)

\(\sigma_1^2 - \sigma_2^2 > 49\)\(\mu < -100\).\(\sigma_1^2 > \sigma_2^2\)\(\sigma_1 - \sigma_2 < 45\)\(\sigma_1 - \sigma_2 = 79\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0985917447)

\(\sigma_1^2 - \sigma_2^2 < -2\)\(\sigma_1^2 > \sigma_2^2\)\(\theta_1 - \theta_2 > -79\)\(\mu_1 - \mu_2 < -70\)\(\sigma_1^2 - \sigma_2^2 \geq 5\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0221591977)

\(\theta_1 - \theta_2 > -99\)\(\mu > 58\).\(\sigma^2 \leq 75\).\(\sigma_1 - \sigma_2 \neq -35\)\(\sigma > 10\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0161610547)

\(\theta \leq 89\).\(\sigma_1^2 \leq \sigma_2^2\)\(\mu_1 \geq \mu_2\)\(\mu_1 - \mu_2 = -63\)\(\sigma_1^2 - \sigma_2^2 < -91\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0436508857)

\(\sigma > 21\).\(\theta \neq -15\).\(\sigma^2 > 21\).\(\sigma_1^2 - \sigma_2^2 < 91\)\(\mu_1 - \mu_2 \leq 96\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0022725396)

\(\mu \leq 1\).\(\theta_1 \leq \theta_2\)\(\sigma^2 \geq 90\).\(\sigma^2 > 76\).\(\sigma_1^2 - \sigma_2^2 \geq 39\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0691754541)

\(\theta_1 \neq \theta_2\)\(\sigma_1^2 \neq \sigma_2^2\)\(\sigma_1 > \sigma_2\)\(\sigma_1 < \sigma_2\)\(\mu \geq -64\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0096514093)

\(\sigma \geq 60\).\(\sigma_1 \leq \sigma_2\)\(\sigma_1^2 - \sigma_2^2 \neq -56\)\(\sigma_1^2 = \sigma_2^2\)\(\sigma_1 = \sigma_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0098701070)

\(\sigma_1 < \sigma_2\)\(\sigma = 46\).\(\theta_1 = \theta_2\)\(\theta_1 \geq \theta_2\)\(\mu_1 = \mu_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0167999236)

\(\sigma > 97\).\(\mu \neq 28\).\(\theta_1 > \theta_2\)\(\theta \neq -72\).\(\sigma \leq 38\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0847069062)

\(\mu_1 > \mu_2\)\(\theta_1 - \theta_2 < -68\)\(\mu_1 - \mu_2 < 9\)\(\mu_1 = \mu_2\)\(\theta_1 < \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0897606128)

\(\sigma^2 \neq 96\).\(\theta \neq 58\).\(\theta_1 - \theta_2 < 33\)\(\mu_1 > \mu_2\)\(\sigma_1^2 \leq \sigma_2^2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0111373322)

\(\theta_1 - \theta_2 \geq -89\)\(\mu_1 = \mu_2\)\(\theta_1 \neq \theta_2\)\(\theta_1 = \theta_2\)\(\theta = 50\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0500862971)

\(\mu > 27\).\(\sigma_1 > \sigma_2\)\(\sigma^2 < 95\).\(\mu \geq 69\).\(\theta_1 > \theta_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0178214057)

\(\theta \leq 68\).\(\sigma_1^2 = \sigma_2^2\)\(\theta_1 - \theta_2 \leq -37\)\(\sigma_1^2 \leq \sigma_2^2\)\(\theta_1 - \theta_2 > -77\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0396076653)

\(\sigma^2 = 93\).\(\sigma \geq 89\).\(\sigma_1 - \sigma_2 = 92\)\(\sigma_1^2 - \sigma_2^2 \leq 66\)\(\sigma_1 - \sigma_2 > 19\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0867586755)

\(\theta_1 \neq \theta_2\)\(\theta_1 - \theta_2 \geq -1\)\(\sigma_1 - \sigma_2 > 35\)\(\sigma_1^2 > \sigma_2^2\)\(\sigma_1 \neq \sigma_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0910430280)

\(\theta_1 > \theta_2\)\(\mu_1 - \mu_2 > -3\)\(\mu_1 = \mu_2\)\(\theta_1 \neq \theta_2\)\(\mu > -43\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0026287469)

\(\mu_1 = \mu_2\)\(\sigma_1 > \sigma_2\)\(\mu_1 \leq \mu_2\)\(\mu = -57\).\(\sigma_1^2 - \sigma_2^2 = -54\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0092007147)

\(\sigma_1 - \sigma_2 \geq 20\)\(\sigma_1^2 - \sigma_2^2 = 64\)\(\sigma_1^2 = \sigma_2^2\)\(\mu \leq -74\).\(\sigma_1^2 - \sigma_2^2 \neq -98\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0777985986)

\(\sigma_1 - \sigma_2 \leq 95\)\(\mu_1 - \mu_2 \neq 23\)\(\mu \neq 82\).\(\theta_1 \neq \theta_2\)\(\sigma_1 - \sigma_2 > -44\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0719292148)

\(\theta = 6\).\(\sigma \geq 16\).\(\sigma_1^2 - \sigma_2^2 \leq -60\)\(\sigma \leq 55\).\(\sigma \neq 11\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0476446560)

\(\sigma_1 - \sigma_2 > -94\)\(\sigma^2 \leq 14\).\(\sigma_1^2 - \sigma_2^2 \geq 49\)\(\sigma_1 \geq \sigma_2\)\(\theta_1 - \theta_2 \leq 96\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0660775097)

\(\sigma_1 \geq \sigma_2\)\(\mu_1 \neq \mu_2\)\(\sigma_1^2 < \sigma_2^2\)\(\sigma_1 - \sigma_2 \neq 12\)\(\theta_1 < \theta_2\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0083269016)

\(\sigma_1 - \sigma_2 > -63\)\(\theta_1 < \theta_2\)\(\sigma_1^2 > \sigma_2^2\)\(\theta_1 - \theta_2 \geq -85\)\(\sigma_1 \neq \sigma_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0847325886)

\(\mu_1 - \mu_2 \leq 27\)\(\mu_1 < \mu_2\)\(\mu_1 \geq \mu_2\)\(\theta \leq -94\).\(\sigma_1^2 - \sigma_2^2 = 82\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0781130657)

\(\sigma_1^2 - \sigma_2^2 = 80\)\(\theta > 71\).\(\mu \geq 62\).\(\theta_1 \leq \theta_2\)\(\mu = -1\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0880535835)

\(\sigma_1^2 - \sigma_2^2 = 74\)\(\mu > -44\).\(\sigma^2 = 80\).\(\sigma_1^2 - \sigma_2^2 \leq 11\)\(\sigma_1 - \sigma_2 \leq -74\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0001692578)

\(\sigma \geq 8\).\(\sigma \neq 76\).\(\theta = 71\).\(\mu \leq -15\).\(\theta_1 - \theta_2 = -47\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0273855123)

\(\sigma_1^2 > \sigma_2^2\)\(\sigma_1^2 \leq \sigma_2^2\)\(\sigma_1 = \sigma_2\)\(\sigma \geq 40\).\(\mu_1 \geq \mu_2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0170852499)

\(\mu_1 = \mu_2\)\(\theta = 42\).\(\theta_1 - \theta_2 = 74\)\(\mu_1 \geq \mu_2\)\(\sigma_1^2 - \sigma_2^2 \neq 0\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0422465073)

\(\sigma_1 - \sigma_2 \leq -63\)\(\sigma_1^2 \neq \sigma_2^2\)\(\theta_1 - \theta_2 \leq 0\)\(\mu_1 = \mu_2\)\(\theta \leq 93\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0548914288)

\(\theta_1 \neq \theta_2\)\(\mu_1 - \mu_2 \geq -88\)\(\mu_1 > \mu_2\)\(\sigma_1^2 < \sigma_2^2\)\(\sigma_1^2 - \sigma_2^2 < -48\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0698454906)

\(\sigma^2 \neq 50\).\(\sigma_1^2 < \sigma_2^2\)\(\theta < 24\).\(\sigma^2 \geq 66\).\(\mu_1 - \mu_2 \neq -56\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0114114071)

\(\sigma_1 < \sigma_2\)\(\theta_1 - \theta_2 < 13\)\(\sigma_1^2 \geq \sigma_2^2\)\(\theta < 23\).\(\sigma_1^2 \neq \sigma_2^2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0376219751)

\(\theta_1 \geq \theta_2\)\(\mu = -40\).\(\sigma^2 \geq 28\).\(\theta_1 - \theta_2 > -19\)\(\theta_1 - \theta_2 = -42\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0036494649)

\(\sigma_1^2 \neq \sigma_2^2\)\(\theta_1 - \theta_2 < 52\)\(\sigma_1^2 < \sigma_2^2\)\(\mu = 36\).\(\sigma_1^2 > \sigma_2^2\)

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0506927243)

\(\theta_1 < \theta_2\)\(\sigma_1 = \sigma_2\)\(\sigma^2 \geq 54\).\(\theta_1 \geq \theta_2\)\(\sigma_1 - \sigma_2 = -41\)

Which of the following statements is a valid null hypothesis?

(Question ID: 0904672155)

\(\theta_1 < \theta_2\)\(\sigma^2 > 8\).\(\mu_1 > \mu_2\)\(\mu = 65\).\(\sigma^2 < 42\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0048619493)

\(\sigma_1^2 \leq \sigma_2^2\)\(\sigma_1 - \sigma_2 \geq -9\)\(\sigma_1 \geq \sigma_2\)\(\sigma^2 \leq 63\).\(\sigma^2 \neq 85\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0209454076)

\(\mu_1 - \mu_2 < -10\)\(\sigma_1^2 \neq \sigma_2^2\)\(\sigma \neq 18\).\(\theta_1 \leq \theta_2\)\(\sigma > 70\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0821994821)

\(\sigma_1^2 - \sigma_2^2 < -67\)\(\theta_1 - \theta_2 > 64\)\(\mu \leq 76\).\(\sigma_1^2 < \sigma_2^2\)\(\mu > -38\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0104792528)

\(\sigma_1 \leq \sigma_2\)\(\mu_1 - \mu_2 = 78\)\(\theta_1 \neq \theta_2\)\(\theta = -12\).\(\mu = 49\).

Which of the following statements is a valid alternative hypothesis?

(Question ID: 0569233504)

\(\theta > -26\).\(\theta_1 \geq \theta_2\)\(\sigma \geq 32\).\(\theta \leq 44\).\(\mu = -62\).

Which of the following statements is a valid null hypothesis?

(Question ID: 0565755884)

\(\mu < 64\).\(\theta > 12\).\(\mu_1 - \mu_2 < -30\)\(\sigma_1^2 - \sigma_2^2 \geq -100\)\(\sigma_1 > \sigma_2\)

Self Assessment 15.3

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.2458\) and \(\alpha=0.025\).\(p=0.6714\) and \(\alpha=0.08\).\(p=0.0077\) and \(\alpha=0.075\).\(p=0.0358\) and \(\alpha=0.035\).\(p=0.0978\) and \(\alpha=0.05\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0809\) and \(\alpha=0.08\).\(p=0.0820\) and \(\alpha=0.085\).\(p=0.1507\) and \(\alpha=0.1\).\(p=0.6466\) and \(\alpha=0.005\).\(p=0.0238\) and \(\alpha=0.015\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0076\) and \(\alpha=0.015\).\(p=0.0673\) and \(\alpha=0.075\).\(p=0.0701\) and \(\alpha=0.09\).\(p=0.0828\) and \(\alpha=0.045\).\(p=0.0034\) and \(\alpha=0.06\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1388\) and \(\alpha=0.095\).\(p=0.6960\) and \(\alpha=0.09\).\(p=0.0486\) and \(\alpha=0.055\).\(p=0.0354\) and \(\alpha=0.035\).\(p=0.3903\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0706\) and \(\alpha=0.04\).\(p=0.0055\) and \(\alpha=0.095\).\(p=0.5021\) and \(\alpha=0.005\).\(p=0.0655\) and \(\alpha=0.065\).\(p=0.0791\) and \(\alpha=0.035\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0210\) and \(\alpha=0.02\).\(p=0.0068\) and \(\alpha=0.01\).\(p=0.7310\) and \(\alpha=0.095\).\(p=0.0751\) and \(\alpha=0.035\).\(p=0.0616\) and \(\alpha=0.055\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0059\) and \(\alpha=0.005\).\(p=0.0223\) and \(\alpha=0.035\).\(p=0.3284\) and \(\alpha=0.055\).\(p=0.1350\) and \(\alpha=0.09\).\(p=0.7756\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0019\) and \(\alpha=0.005\).\(p=0.0194\) and \(\alpha=0.05\).\(p=0.0251\) and \(\alpha=0.045\).\(p=0.0210\) and \(\alpha=0.09\).\(p=0.1003\) and \(\alpha=0.1\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.8174\) and \(\alpha=0.02\).\(p=0.0062\) and \(\alpha=0.005\).\(p=0.1283\) and \(\alpha=0.065\).\(p=0.0076\) and \(\alpha=0.035\).\(p=0.0501\) and \(\alpha=0.05\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.6627\) and \(\alpha=0.095\).\(p=0.0452\) and \(\alpha=0.025\).\(p=0.0062\) and \(\alpha=0.065\).\(p=0.0158\) and \(\alpha=0.015\).\(p=0.1081\) and \(\alpha=0.055\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1008\) and \(\alpha=0.1\).\(p=0.1262\) and \(\alpha=0.05\).\(p=0.1542\) and \(\alpha=0.09\).\(p=0.6889\) and \(\alpha=0.065\).\(p=0.0113\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.4115\) and \(\alpha=0.02\).\(p=0.0804\) and \(\alpha=0.08\).\(p=0.5708\) and \(\alpha=0.09\).\(p=0.0520\) and \(\alpha=0.03\).\(p=0.0241\) and \(\alpha=0.085\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0952\) and \(\alpha=0.095\).\(p=0.9830\) and \(\alpha=0.085\).\(p=0.0414\) and \(\alpha=0.03\).\(p=0.1581\) and \(\alpha=0.07\).\(p=0.0540\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0074\) and \(\alpha=0.015\).\(p=0.0116\) and \(\alpha=0.07\).\(p=0.0002\) and \(\alpha=0.01\).\(p=0.0414\) and \(\alpha=0.035\).\(p=0.0189\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0655\) and \(\alpha=0.065\).\(p=0.1213\) and \(\alpha=0.1\).\(p=0.6270\) and \(\alpha=0.06\).\(p=0.1048\) and \(\alpha=0.07\).\(p=0.0086\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0057\) and \(\alpha=0.005\).\(p=0.0874\) and \(\alpha=0.05\).\(p=0.0188\) and \(\alpha=0.04\).\(p=0.6206\) and \(\alpha=0.015\).\(p=0.4302\) and \(\alpha=0.08\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0259\) and \(\alpha=0.03\).\(p=0.0101\) and \(\alpha=0.01\).\(p=0.0025\) and \(\alpha=0.005\).\(p=0.0055\) and \(\alpha=0.075\).\(p=0.0761\) and \(\alpha=0.09\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.8527\) and \(\alpha=0.025\).\(p=0.0838\) and \(\alpha=0.055\).\(p=0.2513\) and \(\alpha=0.085\).\(p=0.0040\) and \(\alpha=0.02\).\(p=0.0605\) and \(\alpha=0.06\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0054\) and \(\alpha=0.005\).\(p=0.1715\) and \(\alpha=0.06\).\(p=0.9776\) and \(\alpha=0.01\).\(p=0.0660\) and \(\alpha=0.065\).\(p=0.0154\) and \(\alpha=0.02\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0257\) and \(\alpha=0.025\).\(p=0.1070\) and \(\alpha=0.065\).\(p=0.4123\) and \(\alpha=0.075\).\(p=0.0345\) and \(\alpha=0.085\).\(p=0.6001\) and \(\alpha=0.09\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0301\) and \(\alpha=0.04\).\(p=0.0256\) and \(\alpha=0.035\).\(p=0.0176\) and \(\alpha=0.07\).\(p=0.4330\) and \(\alpha=0.075\).\(p=0.0049\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1480\) and \(\alpha=0.085\).\(p=0.3642\) and \(\alpha=0.09\).\(p=0.0555\) and \(\alpha=0.06\).\(p=0.0756\) and \(\alpha=0.075\).\(p=0.9600\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.1805\) and \(\alpha=0.09\).\(p=0.0014\) and \(\alpha=0.075\).\(p=0.0378\) and \(\alpha=0.045\).\(p=0.0264\) and \(\alpha=0.095\).\(p=0.0021\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0297\) and \(\alpha=0.085\).\(p=0.3083\) and \(\alpha=0.095\).\(p=0.0599\) and \(\alpha=0.065\).\(p=0.0273\) and \(\alpha=0.04\).\(p=0.0123\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0706\) and \(\alpha=0.07\).\(p=0.0048\) and \(\alpha=0.015\).\(p=0.1203\) and \(\alpha=0.095\).\(p=0.9626\) and \(\alpha=0.075\).\(p=0.0476\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0209\) and \(\alpha=0.02\).\(p=0.1512\) and \(\alpha=0.085\).\(p=0.6214\) and \(\alpha=0.07\).\(p=0.2434\) and \(\alpha=0.04\).\(p=0.0007\) and \(\alpha=0.045\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0493\) and \(\alpha=0.065\).\(p=0.7093\) and \(\alpha=0.075\).\(p=0.0596\) and \(\alpha=0.08\).\(p=0.0175\) and \(\alpha=0.02\).\(p=0.0779\) and \(\alpha=0.095\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0241\) and \(\alpha=0.025\).\(p=0.0214\) and \(\alpha=0.04\).\(p=0.0043\) and \(\alpha=0.005\).\(p=0.1036\) and \(\alpha=0.06\).\(p=0.0031\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1368\) and \(\alpha=0.08\).\(p=0.0746\) and \(\alpha=0.015\).\(p=0.0206\) and \(\alpha=0.02\).\(p=0.0521\) and \(\alpha=0.085\).\(p=0.8909\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0182\) and \(\alpha=0.02\).\(p=0.0036\) and \(\alpha=0.01\).\(p=0.0256\) and \(\alpha=0.09\).\(p=0.0008\) and \(\alpha=0.005\).\(p=0.1008\) and \(\alpha=0.1\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.6759\) and \(\alpha=0.015\).\(p=0.0710\) and \(\alpha=0.07\).\(p=0.2246\) and \(\alpha=0.075\).\(p=0.0494\) and \(\alpha=0.06\).\(p=0.1490\) and \(\alpha=0.1\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.4175\) and \(\alpha=0.07\).\(p=0.0530\) and \(\alpha=0.06\).\(p=0.0225\) and \(\alpha=0.045\).\(p=0.0134\) and \(\alpha=0.08\).\(p=0.0605\) and \(\alpha=0.1\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0332\) and \(\alpha=0.095\).\(p=0.0368\) and \(\alpha=0.065\).\(p=0.0129\) and \(\alpha=0.05\).\(p=0.1236\) and \(\alpha=0.085\).\(p=0.0210\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.8520\) and \(\alpha=0.09\).\(p=0.0604\) and \(\alpha=0.06\).\(p=0.3787\) and \(\alpha=0.02\).\(p=0.0094\) and \(\alpha=0.005\).\(p=0.0219\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0525\) and \(\alpha=0.075\).\(p=0.0660\) and \(\alpha=0.065\).\(p=0.0245\) and \(\alpha=0.025\).\(p=0.0096\) and \(\alpha=0.01\).\(p=0.0094\) and \(\alpha=0.035\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0227\) and \(\alpha=0.04\).\(p=0.0019\) and \(\alpha=0.01\).\(p=0.0240\) and \(\alpha=0.07\).\(p=0.1880\) and \(\alpha=0.005\).\(p=0.0145\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0632\) and \(\alpha=0.08\).\(p=0.4494\) and \(\alpha=0.09\).\(p=0.0373\) and \(\alpha=0.07\).\(p=0.0251\) and \(\alpha=0.055\).\(p=0.0229\) and \(\alpha=0.045\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.2182\) and \(\alpha=0.02\).\(p=0.0121\) and \(\alpha=0.04\).\(p=0.0067\) and \(\alpha=0.055\).\(p=0.0100\) and \(\alpha=0.045\).\(p=0.0118\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0196\) and \(\alpha=0.095\).\(p=0.3583\) and \(\alpha=0.03\).\(p=0.0399\) and \(\alpha=0.055\).\(p=0.0426\) and \(\alpha=0.09\).\(p=0.0055\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.5947\) and \(\alpha=0.08\).\(p=0.0166\) and \(\alpha=0.015\).\(p=0.0116\) and \(\alpha=0.04\).\(p=0.0758\) and \(\alpha=0.075\).\(p=0.2822\) and \(\alpha=0.05\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.6876\) and \(\alpha=0.085\).\(p=0.0760\) and \(\alpha=0.075\).\(p=0.0212\) and \(\alpha=0.06\).\(p=0.2102\) and \(\alpha=0.05\).\(p=0.0788\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0495\) and \(\alpha=0.085\).\(p=0.0409\) and \(\alpha=0.04\).\(p=0.0107\) and \(\alpha=0.03\).\(p=0.0127\) and \(\alpha=0.025\).\(p=0.0354\) and \(\alpha=0.05\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0206\) and \(\alpha=0.1\).\(p=0.0602\) and \(\alpha=0.05\).\(p=0.9807\) and \(\alpha=0.095\).\(p=0.0109\) and \(\alpha=0.01\).\(p=0.3154\) and \(\alpha=0.06\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0277\) and \(\alpha=0.04\).\(p=0.0006\) and \(\alpha=0.06\).\(p=0.1621\) and \(\alpha=0.05\).\(p=0.0065\) and \(\alpha=0.015\).\(p=0.0060\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.5304\) and \(\alpha=0.085\).\(p=0.0707\) and \(\alpha=0.07\).\(p=0.0390\) and \(\alpha=0.03\).\(p=0.3701\) and \(\alpha=0.08\).\(p=0.0006\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0520\) and \(\alpha=0.085\).\(p=0.0078\) and \(\alpha=0.005\).\(p=0.0017\) and \(\alpha=0.08\).\(p=0.0014\) and \(\alpha=0.02\).\(p=0.0179\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.3120\) and \(\alpha=0.01\).\(p=0.0208\) and \(\alpha=0.015\).\(p=0.0352\) and \(\alpha=0.035\).\(p=0.6285\) and \(\alpha=0.085\).\(p=0.0111\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0042\) and \(\alpha=0.005\).\(p=0.0251\) and \(\alpha=0.025\).\(p=0.0230\) and \(\alpha=0.02\).\(p=0.5552\) and \(\alpha=0.07\).\(p=0.4816\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0115\) and \(\alpha=0.015\).\(p=0.0181\) and \(\alpha=0.025\).\(p=0.0409\) and \(\alpha=0.04\).\(p=0.0670\) and \(\alpha=0.095\).\(p=0.0542\) and \(\alpha=0.085\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0257\) and \(\alpha=0.025\).\(p=0.0648\) and \(\alpha=0.045\).\(p=0.0002\) and \(\alpha=0.01\).\(p=0.5528\) and \(\alpha=0.035\).\(p=0.1633\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.6326\) and \(\alpha=0.04\).\(p=0.0302\) and \(\alpha=0.08\).\(p=0.1026\) and \(\alpha=0.085\).\(p=0.4650\) and \(\alpha=0.065\).\(p=0.0309\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0153\) and \(\alpha=0.035\).\(p=0.0055\) and \(\alpha=0.045\).\(p=0.3539\) and \(\alpha=0.06\).\(p=0.0691\) and \(\alpha=0.08\).\(p=0.0054\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0095\) and \(\alpha=0.01\).\(p=0.0107\) and \(\alpha=0.095\).\(p=0.0212\) and \(\alpha=0.1\).\(p=0.0384\) and \(\alpha=0.085\).\(p=0.9586\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0906\) and \(\alpha=0.055\).\(p=0.0370\) and \(\alpha=0.05\).\(p=0.0960\) and \(\alpha=0.095\).\(p=0.2774\) and \(\alpha=0.065\).\(p=0.7789\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.7686\) and \(\alpha=0.025\).\(p=0.0103\) and \(\alpha=0.05\).\(p=0.0026\) and \(\alpha=0.1\).\(p=0.0390\) and \(\alpha=0.045\).\(p=0.0301\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0060\) and \(\alpha=0.025\).\(p=0.0798\) and \(\alpha=0.05\).\(p=0.0169\) and \(\alpha=0.035\).\(p=0.0696\) and \(\alpha=0.1\).\(p=0.0522\) and \(\alpha=0.09\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0089\) and \(\alpha=0.02\).\(p=0.0354\) and \(\alpha=0.035\).\(p=0.0471\) and \(\alpha=0.065\).\(p=0.0474\) and \(\alpha=0.075\).\(p=0.0067\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0029\) and \(\alpha=0.005\).\(p=0.0467\) and \(\alpha=0.095\).\(p=0.0551\) and \(\alpha=0.07\).\(p=0.0025\) and \(\alpha=0.04\).\(p=0.0157\) and \(\alpha=0.015\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0406\) and \(\alpha=0.06\).\(p=0.0055\) and \(\alpha=0.005\).\(p=0.0364\) and \(\alpha=0.085\).\(p=0.0447\) and \(\alpha=0.055\).\(p=0.0264\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.3942\) and \(\alpha=0.04\).\(p=0.0356\) and \(\alpha=0.035\).\(p=0.7183\) and \(\alpha=0.005\).\(p=0.1210\) and \(\alpha=0.095\).\(p=0.0178\) and \(\alpha=0.02\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0179\) and \(\alpha=0.03\).\(p=0.0787\) and \(\alpha=0.1\).\(p=0.0369\) and \(\alpha=0.04\).\(p=0.3196\) and \(\alpha=0.035\).\(p=0.0172\) and \(\alpha=0.085\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.1218\) and \(\alpha=0.07\).\(p=0.0154\) and \(\alpha=0.05\).\(p=0.0027\) and \(\alpha=0.01\).\(p=0.0021\) and \(\alpha=0.005\).\(p=0.0241\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1208\) and \(\alpha=0.08\).\(p=0.9174\) and \(\alpha=0.06\).\(p=0.3784\) and \(\alpha=0.09\).\(p=0.0455\) and \(\alpha=0.045\).\(p=0.0061\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.6306\) and \(\alpha=0.005\).\(p=0.0141\) and \(\alpha=0.045\).\(p=0.0130\) and \(\alpha=0.025\).\(p=0.0457\) and \(\alpha=0.05\).\(p=0.0886\) and \(\alpha=0.095\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1302\) and \(\alpha=0.1\).\(p=0.0254\) and \(\alpha=0.025\).\(p=0.0369\) and \(\alpha=0.045\).\(p=0.3918\) and \(\alpha=0.07\).\(p=0.5200\) and \(\alpha=0.095\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0097\) and \(\alpha=0.08\).\(p=0.0155\) and \(\alpha=0.02\).\(p=0.3274\) and \(\alpha=0.04\).\(p=0.0870\) and \(\alpha=0.09\).\(p=0.0147\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0183\) and \(\alpha=0.045\).\(p=0.0023\) and \(\alpha=0.005\).\(p=0.1058\) and \(\alpha=0.06\).\(p=0.0079\) and \(\alpha=0.07\).\(p=0.0239\) and \(\alpha=0.025\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0786\) and \(\alpha=0.045\).\(p=0.0806\) and \(\alpha=0.08\).\(p=0.0305\) and \(\alpha=0.065\).\(p=0.2151\) and \(\alpha=0.02\).\(p=0.8649\) and \(\alpha=0.035\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0720\) and \(\alpha=0.085\).\(p=0.0185\) and \(\alpha=0.05\).\(p=0.0443\) and \(\alpha=0.09\).\(p=0.0104\) and \(\alpha=0.015\).\(p=0.6211\) and \(\alpha=0.1\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0084\) and \(\alpha=0.01\).\(p=0.0442\) and \(\alpha=0.06\).\(p=0.0037\) and \(\alpha=0.005\).\(p=0.0146\) and \(\alpha=0.02\).\(p=0.0302\) and \(\alpha=0.03\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0302\) and \(\alpha=0.09\).\(p=0.0580\) and \(\alpha=0.07\).\(p=0.1049\) and \(\alpha=0.08\).\(p=0.0324\) and \(\alpha=0.06\).\(p=0.0616\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0256\) and \(\alpha=0.025\).\(p=0.2775\) and \(\alpha=0.06\).\(p=0.5766\) and \(\alpha=0.04\).\(p=0.0626\) and \(\alpha=0.065\).\(p=0.0288\) and \(\alpha=0.02\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0519\) and \(\alpha=0.095\).\(p=0.0046\) and \(\alpha=0.06\).\(p=0.0156\) and \(\alpha=0.03\).\(p=0.0619\) and \(\alpha=0.07\).\(p=0.3475\) and \(\alpha=0.005\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0609\) and \(\alpha=0.06\).\(p=0.1082\) and \(\alpha=0.1\).\(p=0.1438\) and \(\alpha=0.075\).\(p=0.0018\) and \(\alpha=0.02\).\(p=0.8638\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0434\) and \(\alpha=0.035\).\(p=0.0106\) and \(\alpha=0.01\).\(p=0.1752\) and \(\alpha=0.1\).\(p=0.6950\) and \(\alpha=0.03\).\(p=0.0011\) and \(\alpha=0.005\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.1409\) and \(\alpha=0.07\).\(p=0.0814\) and \(\alpha=0.09\).\(p=0.0134\) and \(\alpha=0.015\).\(p=0.0069\) and \(\alpha=0.03\).\(p=0.0298\) and \(\alpha=0.055\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0033\) and \(\alpha=0.005\).\(p=0.0506\) and \(\alpha=0.07\).\(p=0.6964\) and \(\alpha=0.095\).\(p=0.0124\) and \(\alpha=0.025\).\(p=0.0481\) and \(\alpha=0.075\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0802\) and \(\alpha=0.08\).\(p=0.1885\) and \(\alpha=0.095\).\(p=0.1552\) and \(\alpha=0.1\).\(p=0.8506\) and \(\alpha=0.085\).\(p=0.0001\) and \(\alpha=0.045\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0413\) and \(\alpha=0.07\).\(p=0.8002\) and \(\alpha=0.02\).\(p=0.1342\) and \(\alpha=0.075\).\(p=0.3947\) and \(\alpha=0.04\).\(p=0.0557\) and \(\alpha=0.055\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1442\) and \(\alpha=0.08\).\(p=0.0558\) and \(\alpha=0.085\).\(p=0.9009\) and \(\alpha=0.07\).\(p=0.1597\) and \(\alpha=0.065\).\(p=0.0406\) and \(\alpha=0.04\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0610\) and \(\alpha=0.1\).\(p=0.0224\) and \(\alpha=0.06\).\(p=0.0363\) and \(\alpha=0.09\).\(p=0.0065\) and \(\alpha=0.01\).\(p=0.1742\) and \(\alpha=0.065\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0006\) and \(\alpha=0.035\).\(p=0.0733\) and \(\alpha=0.075\).\(p=0.0655\) and \(\alpha=0.065\).\(p=0.0486\) and \(\alpha=0.05\).\(p=0.0369\) and \(\alpha=0.09\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0061\) and \(\alpha=0.01\).\(p=0.0590\) and \(\alpha=0.06\).\(p=0.1568\) and \(\alpha=0.08\).\(p=0.0014\) and \(\alpha=0.025\).\(p=0.0026\) and \(\alpha=0.005\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0187\) and \(\alpha=0.055\).\(p=0.0692\) and \(\alpha=0.075\).\(p=0.0668\) and \(\alpha=0.07\).\(p=0.0478\) and \(\alpha=0.085\).\(p=0.7027\) and \(\alpha=0.035\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.5299\) and \(\alpha=0.035\).\(p=0.1652\) and \(\alpha=0.1\).\(p=0.0634\) and \(\alpha=0.09\).\(p=0.4353\) and \(\alpha=0.04\).\(p=0.0557\) and \(\alpha=0.055\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0091\) and \(\alpha=0.095\).\(p=0.0041\) and \(\alpha=0.075\).\(p=0.0092\) and \(\alpha=0.01\).\(p=0.0408\) and \(\alpha=0.03\).\(p=0.0347\) and \(\alpha=0.045\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.8073\) and \(\alpha=0.075\).\(p=0.1016\) and \(\alpha=0.06\).\(p=0.0549\) and \(\alpha=0.095\).\(p=0.0254\) and \(\alpha=0.02\).\(p=0.0105\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0152\) and \(\alpha=0.055\).\(p=0.0146\) and \(\alpha=0.06\).\(p=0.0232\) and \(\alpha=0.07\).\(p=0.0197\) and \(\alpha=0.025\).\(p=0.1039\) and \(\alpha=0.045\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0019\) and \(\alpha=0.025\).\(p=0.0284\) and \(\alpha=0.085\).\(p=0.0167\) and \(\alpha=0.05\).\(p=0.0048\) and \(\alpha=0.005\).\(p=0.2244\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0736\) and \(\alpha=0.065\).\(p=0.0321\) and \(\alpha=0.045\).\(p=0.0803\) and \(\alpha=0.09\).\(p=0.0292\) and \(\alpha=0.03\).\(p=0.0021\) and \(\alpha=0.005\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.1320\) and \(\alpha=0.1\).\(p=0.0552\) and \(\alpha=0.075\).\(p=0.0046\) and \(\alpha=0.08\).\(p=0.0486\) and \(\alpha=0.055\).\(p=0.0140\) and \(\alpha=0.06\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0546\) and \(\alpha=0.065\).\(p=0.0692\) and \(\alpha=0.05\).\(p=0.0611\) and \(\alpha=0.045\).\(p=0.9432\) and \(\alpha=0.095\).\(p=0.0755\) and \(\alpha=0.075\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0158\) and \(\alpha=0.015\).\(p=0.0215\) and \(\alpha=0.05\).\(p=0.0392\) and \(\alpha=0.02\).\(p=0.4744\) and \(\alpha=0.09\).\(p=0.5128\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.7112\) and \(\alpha=0.065\).\(p=0.0108\) and \(\alpha=0.045\).\(p=0.2162\) and \(\alpha=0.07\).\(p=0.0398\) and \(\alpha=0.035\).\(p=0.0801\) and \(\alpha=0.08\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0614\) and \(\alpha=0.075\).\(p=0.0255\) and \(\alpha=0.035\).\(p=0.7836\) and \(\alpha=0.03\).\(p=0.0898\) and \(\alpha=0.095\).\(p=0.0097\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0095\) and \(\alpha=0.045\).\(p=0.1100\) and \(\alpha=0.07\).\(p=0.0230\) and \(\alpha=0.025\).\(p=0.0180\) and \(\alpha=0.06\).\(p=0.0044\) and \(\alpha=0.01\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0014\) and \(\alpha=0.005\).\(p=0.1082\) and \(\alpha=0.09\).\(p=0.0807\) and \(\alpha=0.08\).\(p=0.6853\) and \(\alpha=0.035\).\(p=0.3640\) and \(\alpha=0.07\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.1147\) and \(\alpha=0.005\).\(p=0.0030\) and \(\alpha=0.01\).\(p=0.8162\) and \(\alpha=0.1\).\(p=0.0810\) and \(\alpha=0.08\).\(p=0.1278\) and \(\alpha=0.095\).

A statistical hypothesis test is run. It is a two-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher reject the null hypothesis?

\(p=0.0692\) and \(\alpha=0.055\).\(p=0.0022\) and \(\alpha=0.005\).\(p=0.3093\) and \(\alpha=0.05\).\(p=0.0404\) and \(\alpha=0.04\).\(p=0.6057\) and \(\alpha=0.09\).

A statistical hypothesis test is run. It is a one-tailed test. For which of the following \(p\)-value / level of significance pairs would the researcher fail to reject the null hypothesis?

\(p=0.0064\) and \(\alpha=0.055\).\(p=0.0202\) and \(\alpha=0.025\).\(p=0.0179\) and \(\alpha=0.065\).\(p=0.9843\) and \(\alpha=0.085\).\(p=0.0046\) and \(\alpha=0.09\).

Self Assessment 15.4

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 160.23 . To understand the impact of the diet, they randomly select 70 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 161.8 and a sample standard deviation of 7.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0584416063

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 79 . To test the new method, they randomly sample 61 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 82.4 and a sample standard deviation of 8.05.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0926042361

A factory that fills food containers has a process that is meant to fill individual boxes to 400 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 75 boxes, weighing them. They find a sample mean of 402.3 and a sample standard deviation of 8.58.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0591999135

A factory that fills food containers has a process that is meant to fill individual boxes to 554 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 47 boxes, weighing them. They find a sample mean of 553.3 and a sample standard deviation of 6.99.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0123075359

A factory that fills food containers has a process that is meant to fill individual boxes to 562 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 93 boxes, weighing them. They find a sample mean of 564 and a sample standard deviation of 9.6.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0651962371

A large chain coffee shop claims that their lattes have 158 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 91 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 159.2 and a sample standard deviation of 3.57.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0439477241

A large chain coffee shop claims that their lattes have 147 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 47 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 147.3 and a sample standard deviation of 3.01.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0812454485

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.6559 seconds. The researchers randomly sample 60 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.0583.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0435672142

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 144.43 . To understand the impact of the diet, they randomly select 83 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 143.1 and a sample standard deviation of 6.48.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0743716960

A factory that fills food containers has a process that is meant to fill individual boxes to 457 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 52 boxes, weighing them. They find a sample mean of 457.5 and a sample standard deviation of 5.04.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0880189985

A factory that fills food containers has a process that is meant to fill individual boxes to 600 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 86 boxes, weighing them. They find a sample mean of 599.1 and a sample standard deviation of 5.93.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0287455383

A factory that fills food containers has a process that is meant to fill individual boxes to 588 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 53 boxes, weighing them. They find a sample mean of 589.7 and a sample standard deviation of 5.44.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0259397751

A factory that fills food containers has a process that is meant to fill individual boxes to 416 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 86 boxes, weighing them. They find a sample mean of 414.3 and a sample standard deviation of 6.12.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0424316137

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 71 . To test the new method, they randomly sample 41 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 73.7 and a sample standard deviation of 6.41.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0512803976

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 105 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 91 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 105.7 and a sample standard deviation of 6.3.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0958254505

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 74 . To test the new method, they randomly sample 55 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 74.4 and a sample standard deviation of 7.08.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0232428551

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 70 . To test the new method, they randomly sample 35 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 68.4 and a sample standard deviation of 9.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0938696636

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.6845 seconds. The researchers randomly sample 44 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0953.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0261820740

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 129 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 82 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 129.7 and a sample standard deviation of 6.1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0559589491

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.4500 seconds. The researchers randomly sample 85 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0873.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0338354875

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.5355 seconds. The researchers randomly sample 49 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0519.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0652205871

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 104 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 53 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 102.1 and a sample standard deviation of 6.71.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0807598018

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.3960 seconds. The researchers randomly sample 56 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0823.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0372255639

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 77 . To test the new method, they randomly sample 67 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 78.8 and a sample standard deviation of 8.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0026009284

A large chain coffee shop claims that their lattes have 140 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 91 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 141.8 and a sample standard deviation of 4.58.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0518746393

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 171.65 . To understand the impact of the diet, they randomly select 39 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 170.5 and a sample standard deviation of 9.01.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0414441233

A factory that fills food containers has a process that is meant to fill individual boxes to 535 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 77 boxes, weighing them. They find a sample mean of 536.7 and a sample standard deviation of 5.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0899338266

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 71 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 87 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 74.1 and a sample standard deviation of 17.82.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0509070730

A large chain coffee shop claims that their lattes have 151 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 92 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 151.2 and a sample standard deviation of 3.26.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0028780449

A large chain coffee shop claims that their lattes have 156 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 78 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 154.7 and a sample standard deviation of 4.67.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0423356580

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 86 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 78.9 and a sample standard deviation of 8.47.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0961151215

A large chain coffee shop claims that their lattes have 140 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 64 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 139.6 and a sample standard deviation of 4.03.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0579102009

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 79 . To test the new method, they randomly sample 66 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 79.4 and a sample standard deviation of 6.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0579599028

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.3816 seconds. The researchers randomly sample 65 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0657.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0765811964

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 165.5 . To understand the impact of the diet, they randomly select 92 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 165.3 and a sample standard deviation of 5.14.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0134348236

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.4582 seconds. The researchers randomly sample 68 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0734.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0486931161

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.4071 seconds. The researchers randomly sample 80 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0832.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0718167707

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 172 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 46 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 169.6 and a sample standard deviation of 15.55.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0345620119

A factory that fills food containers has a process that is meant to fill individual boxes to 450 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 90 boxes, weighing them. They find a sample mean of 449 and a sample standard deviation of 5.86.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0805834907

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.6916 seconds. The researchers randomly sample 73 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0604.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0122145442

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 107 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 68 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 104.2 and a sample standard deviation of 11.22.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0004233906

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.6926 seconds. The researchers randomly sample 94 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0771.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0337176952

A large chain coffee shop claims that their lattes have 150 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 90 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 149.7 and a sample standard deviation of 3.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0742481994

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 159.72 . To understand the impact of the diet, they randomly select 68 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 162.4 and a sample standard deviation of 9.23.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0514383582

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.4832 seconds. The researchers randomly sample 71 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.073.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0899771533

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 155.03 . To understand the impact of the diet, they randomly select 38 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 152.1 and a sample standard deviation of 14.95.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0720907369

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 132 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 63 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 133.5 and a sample standard deviation of 7.04.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0108257699

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 158.36 . To understand the impact of the diet, they randomly select 99 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 160.2 and a sample standard deviation of 5.81.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0370908153

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 81 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 41 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 79.1 and a sample standard deviation of 13.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0471112685

A large chain coffee shop claims that their lattes have 147 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 35 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 147.4 and a sample standard deviation of 3.1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0764802792

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 172.79 . To understand the impact of the diet, they randomly select 69 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 169.6 and a sample standard deviation of 11.68.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0139361779

A factory that fills food containers has a process that is meant to fill individual boxes to 558 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 37 boxes, weighing them. They find a sample mean of 560.3 and a sample standard deviation of 8.14.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0121446783

A large chain coffee shop claims that their lattes have 151 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 48 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 151.4 and a sample standard deviation of 4.64.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0122626445

A large chain coffee shop claims that their lattes have 154 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 83 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 154.5 and a sample standard deviation of 4.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0279511679

A large chain coffee shop claims that their lattes have 151 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 97 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 150.3 and a sample standard deviation of 3.34.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0665178216

A factory that fills food containers has a process that is meant to fill individual boxes to 473 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 70 boxes, weighing them. They find a sample mean of 472.2 and a sample standard deviation of 8.22.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0850430309

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.3887 seconds. The researchers randomly sample 80 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0944.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0538899665

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 80 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 58 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 79.3 and a sample standard deviation of 6.78.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0677580622

A factory that fills food containers has a process that is meant to fill individual boxes to 580 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 100 boxes, weighing them. They find a sample mean of 577.9 and a sample standard deviation of 9.04.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0417145992

A large chain coffee shop claims that their lattes have 142 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 70 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 142.7 and a sample standard deviation of 4.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0971904871

A large chain coffee shop claims that their lattes have 140 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 79 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 139.8 and a sample standard deviation of 4.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0110290689

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.5290 seconds. The researchers randomly sample 93 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0918.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0887027165

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 153.16 . To understand the impact of the diet, they randomly select 98 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 151.5 and a sample standard deviation of 8.32.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0630575441

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 177.5 . To understand the impact of the diet, they randomly select 67 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 179.5 and a sample standard deviation of 14.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0537624752

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 127 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 52 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 126.5 and a sample standard deviation of 7.79.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0308166804

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.5219 seconds. The researchers randomly sample 77 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0783.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0469075955

A factory that fills food containers has a process that is meant to fill individual boxes to 459 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 48 boxes, weighing them. They find a sample mean of 455.9 and a sample standard deviation of 8.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0827940534

A factory that fills food containers has a process that is meant to fill individual boxes to 404 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 80 boxes, weighing them. They find a sample mean of 403.3 and a sample standard deviation of 7.15.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0182670418

A large chain coffee shop claims that their lattes have 153 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 59 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 153.2 and a sample standard deviation of 4.1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0890063525

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 65 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 79.3 and a sample standard deviation of 8.13.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0625459722

A large chain coffee shop claims that their lattes have 152 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 77 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 150.9 and a sample standard deviation of 3.48.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0460565447

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 73 . To test the new method, they randomly sample 99 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 70.5 and a sample standard deviation of 8.67.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0412961847

A large chain coffee shop claims that their lattes have 151 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 86 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 151.7 and a sample standard deviation of 3.55.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0517336645

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 71 . To test the new method, they randomly sample 100 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 72.6 and a sample standard deviation of 5.69.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0946557678

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 83 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 38 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 81.6 and a sample standard deviation of 14.49.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0917130301

A factory that fills food containers has a process that is meant to fill individual boxes to 489 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 45 boxes, weighing them. They find a sample mean of 487.6 and a sample standard deviation of 7.88.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0097503552

A factory that fills food containers has a process that is meant to fill individual boxes to 432 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 100 boxes, weighing them. They find a sample mean of 435.1 and a sample standard deviation of 8.58.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0017075039

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 55 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 84 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 51.6 and a sample standard deviation of 10.21.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0160116848

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 50 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 73 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 51.3 and a sample standard deviation of 3.95.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0527495428

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 168.76 . To understand the impact of the diet, they randomly select 52 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 171.2 and a sample standard deviation of 5.56.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0642472984

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 71 . To test the new method, they randomly sample 55 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 71.4 and a sample standard deviation of 5.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0303415400

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 159.34 . To understand the impact of the diet, they randomly select 42 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 162.2 and a sample standard deviation of 9.73.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0573205822

A factory that fills food containers has a process that is meant to fill individual boxes to 412 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 70 boxes, weighing them. They find a sample mean of 412.5 and a sample standard deviation of 6.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0692129188

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 73 . To test the new method, they randomly sample 72 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 70.4 and a sample standard deviation of 7.26.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0351556765

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 163.03 . To understand the impact of the diet, they randomly select 70 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 165.8 and a sample standard deviation of 11.3.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0645935948

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 55 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 71 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 54.1 and a sample standard deviation of 12.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0061142105

A large chain coffee shop claims that their lattes have 142 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 88 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 141.6 and a sample standard deviation of 4.9.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0725084912

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 89 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 76.3 and a sample standard deviation of 6.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0559040729

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 113 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 52 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 110.6 and a sample standard deviation of 18.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0385459763

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 77 . To test the new method, they randomly sample 35 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 76.3 and a sample standard deviation of 5.73.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0538294499

A large chain coffee shop claims that their lattes have 150 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 64 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 149.4 and a sample standard deviation of 2.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0213214356

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 148.26 . To understand the impact of the diet, they randomly select 57 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 146.1 and a sample standard deviation of 7.17.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0662173726

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 88 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 80.9 and a sample standard deviation of 9.13.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0493729685

A factory that fills food containers has a process that is meant to fill individual boxes to 433 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 67 boxes, weighing them. They find a sample mean of 430.2 and a sample standard deviation of 9.46.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0481590360

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 162.44 . To understand the impact of the diet, they randomly select 46 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 166.1 and a sample standard deviation of 9.88.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0565651215

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 152.86 . To understand the impact of the diet, they randomly select 68 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 151.8 and a sample standard deviation of 10.54.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0992456491

A researcher is studying the impact of a particular drug on human reaction times. They want to know whether the drug impacts reaction times, compared to average. They know that the average reaction time for subjects without the drug in the task is 0.5901 seconds. The researchers randomly sample 54 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.0984.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0372747309

A factory that fills food containers has a process that is meant to fill individual boxes to 599 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 72 boxes, weighing them. They find a sample mean of 598.6 and a sample standard deviation of 9.48.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0291895920

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 165.66 . To understand the impact of the diet, they randomly select 48 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 166.2 and a sample standard deviation of 10.35.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0124806366

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 71 . To test the new method, they randomly sample 99 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 70.2 and a sample standard deviation of 5.16.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0148223270

Self Assessment 15.5

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 3.82 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 79 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 3.7 and a sample standard deviation of 1.27.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0264909953

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 169.52 . To test its efficacy, researchers take a sample of 63 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 168.1 and a sample standard deviation of 14.24.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0416036924

A phone manufacturer claims that their phone batteries last for an average of 44.65 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 39 phones, testing the battery life, and find a sample mean of 45.83 and a sample standard deviation of 3.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0827285669

A cloud server host is contractually obligated to maintain a server load time of no more than 288.94 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 97 page visits, recording the load time for each, and find a sample mean of 277.71 and a sample standard deviation of 120.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0722922264

A coffee shop chain claims that their average cup of coffee contains 10.94 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.94 ounces. They randomly sample 81 cups of coffee from various locations and find a sample mean of 10.99 and a sample standard deviation of 1.15.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0317149780

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 12.79 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 39 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 13.16 and a sample standard deviation of 2.97.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0100409021

A cloud server host is contractually obligated to maintain a server load time of no more than 420.89 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 71 page visits, recording the load time for each, and find a sample mean of 393.06 and a sample standard deviation of 79.86.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0114518612

A phone manufacturer claims that their phone batteries last for an average of 35.75 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 93 phones, testing the battery life, and find a sample mean of 35.87 and a sample standard deviation of 1.24.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0859138268

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 4.91 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 50 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.6 and a sample standard deviation of 1.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0558332409

A phone manufacturer claims that their phone batteries last for an average of 36.37 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 95 phones, testing the battery life, and find a sample mean of 35.39 and a sample standard deviation of 4.92.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0134322194

A phone manufacturer claims that their phone batteries last for an average of 23.06 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 77 phones, testing the battery life, and find a sample mean of 23.03 and a sample standard deviation of 1.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0569003433

A coffee shop chain claims that their average cup of coffee contains 12.89 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.89 ounces. They randomly sample 81 cups of coffee from various locations and find a sample mean of 13.06 and a sample standard deviation of 1.23.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0672450762

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 143.95 . To test its efficacy, researchers take a sample of 45 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 143.53 and a sample standard deviation of 11.94.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0674203050

A cloud server host is contractually obligated to maintain a server load time of no more than 365.70 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 72 page visits, recording the load time for each, and find a sample mean of 343.02 and a sample standard deviation of 106.84.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0771968248

A phone manufacturer claims that their phone batteries last for an average of 21.73 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 98 phones, testing the battery life, and find a sample mean of 20.5 and a sample standard deviation of 3.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0489397120

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 151.79 . To test its efficacy, researchers take a sample of 35 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 152.25 and a sample standard deviation of 7.96.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0600292043

A cloud server host is contractually obligated to maintain a server load time of no more than 137.32 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 65 page visits, recording the load time for each, and find a sample mean of 126.74 and a sample standard deviation of 58.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0549447518

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 2247 hours. To test the new design, the company samples 90 of the new lightbulbs, testing their lifespan, and they find a sample mean of 2215.99 and a sample standard deviation of 105.66.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0515990094

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 177.89 . To test its efficacy, researchers take a sample of 83 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 175.18 and a sample standard deviation of 13.34.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0130229288

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 13145 hours. To test the new design, the company samples 96 of the new lightbulbs, testing their lifespan, and they find a sample mean of 13006.49 and a sample standard deviation of 390.09.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0712764178

A phone manufacturer claims that their phone batteries last for an average of 34.98 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 45 phones, testing the battery life, and find a sample mean of 34.65 and a sample standard deviation of 2.16.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0551044000

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 174.23 . To test its efficacy, researchers take a sample of 91 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 175.87 and a sample standard deviation of 8.98.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0241225274

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 142.28 . To test its efficacy, researchers take a sample of 60 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 142.43 and a sample standard deviation of 6.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0041524247

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 156.66 . To test its efficacy, researchers take a sample of 86 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 155.22 and a sample standard deviation of 8.01.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0031121117

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 9.79 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 86 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 9.06 and a sample standard deviation of 2.53.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0877032525

A coffee shop chain claims that their average cup of coffee contains 12.62 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.62 ounces. They randomly sample 80 cups of coffee from various locations and find a sample mean of 12.74 and a sample standard deviation of 0.49.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0530369303

A cloud server host is contractually obligated to maintain a server load time of no more than 239.79 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 56 page visits, recording the load time for each, and find a sample mean of 251.49 and a sample standard deviation of 106.21.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0094482515

A cloud server host is contractually obligated to maintain a server load time of no more than 493.81 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 68 page visits, recording the load time for each, and find a sample mean of 473.3 and a sample standard deviation of 127.34.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0324421298

A cloud server host is contractually obligated to maintain a server load time of no more than 189.01 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 81 page visits, recording the load time for each, and find a sample mean of 178.27 and a sample standard deviation of 42.82.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0917098601

A coffee shop chain claims that their average cup of coffee contains 10.36 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.36 ounces. They randomly sample 69 cups of coffee from various locations and find a sample mean of 10.22 and a sample standard deviation of 1.02.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0474456315

A coffee shop chain claims that their average cup of coffee contains 12.90 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.90 ounces. They randomly sample 93 cups of coffee from various locations and find a sample mean of 12.71 and a sample standard deviation of 0.58.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0625363054

A cloud server host is contractually obligated to maintain a server load time of no more than 264.04 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 78 page visits, recording the load time for each, and find a sample mean of 214.55 and a sample standard deviation of 110.94.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0674967877

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3398 hours. To test the new design, the company samples 71 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3369.91 and a sample standard deviation of 126.49.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0015664991

A phone manufacturer claims that their phone batteries last for an average of 23.80 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 56 phones, testing the battery life, and find a sample mean of 23.77 and a sample standard deviation of 2.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0078766856

A coffee shop chain claims that their average cup of coffee contains 11.97 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.97 ounces. They randomly sample 54 cups of coffee from various locations and find a sample mean of 11.61 and a sample standard deviation of 1.1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0120297382

A cloud server host is contractually obligated to maintain a server load time of no more than 212.48 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 48 page visits, recording the load time for each, and find a sample mean of 226.56 and a sample standard deviation of 99.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0148541335

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.62 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 54 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 12.95 and a sample standard deviation of 3.79.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0432292338

A phone manufacturer claims that their phone batteries last for an average of 17.35 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 63 phones, testing the battery life, and find a sample mean of 17.54 and a sample standard deviation of 2.95.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0568398099

A phone manufacturer claims that their phone batteries last for an average of 33.07 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 58 phones, testing the battery life, and find a sample mean of 32.84 and a sample standard deviation of 3.31.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0045157272

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 4.89 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 42 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.05 and a sample standard deviation of 1.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0805080722

A coffee shop chain claims that their average cup of coffee contains 13.29 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 13.29 ounces. They randomly sample 49 cups of coffee from various locations and find a sample mean of 13.29 and a sample standard deviation of 1.04.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0250894754

A phone manufacturer claims that their phone batteries last for an average of 36.32 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 49 phones, testing the battery life, and find a sample mean of 35.87 and a sample standard deviation of 5.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0329021256

A phone manufacturer claims that their phone batteries last for an average of 30.14 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 65 phones, testing the battery life, and find a sample mean of 29.88 and a sample standard deviation of 3.2.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0796269287

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 11.53 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 95 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 11.89 and a sample standard deviation of 2.14.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0344558723

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 164.57 . To test its efficacy, researchers take a sample of 100 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 161.26 and a sample standard deviation of 14.5.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0190558404

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 176.34 . To test its efficacy, researchers take a sample of 74 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 174.55 and a sample standard deviation of 11.78.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0103385107

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 7.80 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 49 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 7.8 and a sample standard deviation of 1.79.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0471996840

A coffee shop chain claims that their average cup of coffee contains 13.71 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 13.71 ounces. They randomly sample 83 cups of coffee from various locations and find a sample mean of 13.83 and a sample standard deviation of 0.75.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0765015668

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 164.06 . To test its efficacy, researchers take a sample of 76 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 160.99 and a sample standard deviation of 12.96.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0407090611

A phone manufacturer claims that their phone batteries last for an average of 20.62 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 80 phones, testing the battery life, and find a sample mean of 19.89 and a sample standard deviation of 4.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0846381759

A coffee shop chain claims that their average cup of coffee contains 12.81 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.81 ounces. They randomly sample 66 cups of coffee from various locations and find a sample mean of 12.59 and a sample standard deviation of 1.12.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0036333373

A coffee shop chain claims that their average cup of coffee contains 12.67 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.67 ounces. They randomly sample 45 cups of coffee from various locations and find a sample mean of 12.37 and a sample standard deviation of 0.98.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0004433848

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 156.92 . To test its efficacy, researchers take a sample of 77 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 157.88 and a sample standard deviation of 9.29.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0724049605

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 9.95 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 42 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 9.78 and a sample standard deviation of 1.9.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0221026349

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 14875 hours. To test the new design, the company samples 43 of the new lightbulbs, testing their lifespan, and they find a sample mean of 14915.07 and a sample standard deviation of 515.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0422510854

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 159.90 . To test its efficacy, researchers take a sample of 51 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 157.29 and a sample standard deviation of 8.73.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0148336498

A cloud server host is contractually obligated to maintain a server load time of no more than 94.21 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 61 page visits, recording the load time for each, and find a sample mean of 97.27 and a sample standard deviation of 16.65.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0273033842

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 9850 hours. To test the new design, the company samples 48 of the new lightbulbs, testing their lifespan, and they find a sample mean of 9764.83 and a sample standard deviation of 361.43.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0221704750

A coffee shop chain claims that their average cup of coffee contains 12.81 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.81 ounces. They randomly sample 69 cups of coffee from various locations and find a sample mean of 12.77 and a sample standard deviation of 0.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0694907671

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 155.46 . To test its efficacy, researchers take a sample of 67 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 152.58 and a sample standard deviation of 10.17.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0519327755

A coffee shop chain claims that their average cup of coffee contains 13.35 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 13.35 ounces. They randomly sample 46 cups of coffee from various locations and find a sample mean of 12.93 and a sample standard deviation of 0.91.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0208896213

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 6.19 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 93 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 6.53 and a sample standard deviation of 2.03.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0296003386

A phone manufacturer claims that their phone batteries last for an average of 24.01 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 41 phones, testing the battery life, and find a sample mean of 24.28 and a sample standard deviation of 1.29.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0168350328

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 150.44 . To test its efficacy, researchers take a sample of 75 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 147.63 and a sample standard deviation of 13.48.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0550679697

A cloud server host is contractually obligated to maintain a server load time of no more than 404.09 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 93 page visits, recording the load time for each, and find a sample mean of 386.06 and a sample standard deviation of 123.66.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0734099045

A cloud server host is contractually obligated to maintain a server load time of no more than 213.21 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 99 page visits, recording the load time for each, and find a sample mean of 227.57 and a sample standard deviation of 105.19.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0308191451

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 142.13 . To test its efficacy, researchers take a sample of 49 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 136.18 and a sample standard deviation of 14.75.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0433833258

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 10499 hours. To test the new design, the company samples 88 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10462.5 and a sample standard deviation of 299.59.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0262626712

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 4.23 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 45 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.33 and a sample standard deviation of 0.91.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0752350414

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.02 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 88 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.63 and a sample standard deviation of 1.4.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0318803133

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.67 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 52 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 5.55 and a sample standard deviation of 1.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0830027795

A coffee shop chain claims that their average cup of coffee contains 11.03 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.03 ounces. They randomly sample 63 cups of coffee from various locations and find a sample mean of 11.04 and a sample standard deviation of 0.9.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0237412527

A phone manufacturer claims that their phone batteries last for an average of 35.00 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 98 phones, testing the battery life, and find a sample mean of 34.66 and a sample standard deviation of 2.05.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0052417460

A phone manufacturer claims that their phone batteries last for an average of 24.97 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 93 phones, testing the battery life, and find a sample mean of 24.71 and a sample standard deviation of 1.33.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0890484425

A cloud server host is contractually obligated to maintain a server load time of no more than 311.71 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 74 page visits, recording the load time for each, and find a sample mean of 299.1 and a sample standard deviation of 54.34.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0121023439

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 6.52 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 37 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 7.2 and a sample standard deviation of 2.11.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0510685290

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 178.87 . To test its efficacy, researchers take a sample of 83 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 178.24 and a sample standard deviation of 8.46.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0159973749

A coffee shop chain claims that their average cup of coffee contains 11.28 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.28 ounces. They randomly sample 77 cups of coffee from various locations and find a sample mean of 11.29 and a sample standard deviation of 0.07.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0943795956

A cloud server host is contractually obligated to maintain a server load time of no more than 90.32 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 90 page visits, recording the load time for each, and find a sample mean of 90.29 and a sample standard deviation of 31.12.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0358164423

A phone manufacturer claims that their phone batteries last for an average of 33.03 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 64 phones, testing the battery life, and find a sample mean of 33.85 and a sample standard deviation of 2.53.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0984737831

A coffee shop chain claims that their average cup of coffee contains 10.23 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.23 ounces. They randomly sample 90 cups of coffee from various locations and find a sample mean of 10.36 and a sample standard deviation of 0.99.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0246217284

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 9.24 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 99 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 9.26 and a sample standard deviation of 1.8.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0971365745

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 12533 hours. To test the new design, the company samples 69 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12567.24 and a sample standard deviation of 624.02.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0743625893

A coffee shop chain claims that their average cup of coffee contains 12.32 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.32 ounces. They randomly sample 52 cups of coffee from various locations and find a sample mean of 12.48 and a sample standard deviation of 1.27.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0684003652

A coffee shop chain claims that their average cup of coffee contains 11.22 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.22 ounces. They randomly sample 68 cups of coffee from various locations and find a sample mean of 11.22 and a sample standard deviation of 0.17.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0149466255

A coffee shop chain claims that their average cup of coffee contains 10.86 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.86 ounces. They randomly sample 82 cups of coffee from various locations and find a sample mean of 10.63 and a sample standard deviation of 0.9.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0008523593

A phone manufacturer claims that their phone batteries last for an average of 44.01 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 86 phones, testing the battery life, and find a sample mean of 44.23 and a sample standard deviation of 2.8.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0559978702

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 7.93 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 87 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 8.11 and a sample standard deviation of 2.29.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0797451752

A coffee shop chain claims that their average cup of coffee contains 11.32 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.32 ounces. They randomly sample 75 cups of coffee from various locations and find a sample mean of 11.3 and a sample standard deviation of 0.11.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0270165715

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 173.35 . To test its efficacy, researchers take a sample of 52 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 170.71 and a sample standard deviation of 10.46.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0216669485

A phone manufacturer claims that their phone batteries last for an average of 36.67 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 97 phones, testing the battery life, and find a sample mean of 36.62 and a sample standard deviation of 1.89.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0903485840

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 154.40 . To test its efficacy, researchers take a sample of 88 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 151.59 and a sample standard deviation of 14.1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0986012558

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 174.25 . To test its efficacy, researchers take a sample of 59 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 171.95 and a sample standard deviation of 14.44.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0648828775

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 11.83 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 85 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 11.56 and a sample standard deviation of 2.82.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0003781727

A cloud server host is contractually obligated to maintain a server load time of no more than 297.82 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 67 page visits, recording the load time for each, and find a sample mean of 306.23 and a sample standard deviation of 62.72.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0487070456

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 7.22 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 87 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 7.1 and a sample standard deviation of 2.15.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0415106446

A cloud server host is contractually obligated to maintain a server load time of no more than 295.07 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 82 page visits, recording the load time for each, and find a sample mean of 319.66 and a sample standard deviation of 132.31.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0301602273

A coffee shop chain claims that their average cup of coffee contains 11.87 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.87 ounces. They randomly sample 97 cups of coffee from various locations and find a sample mean of 11.88 and a sample standard deviation of 0.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0932334197

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 10879 hours. To test the new design, the company samples 98 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10697.65 and a sample standard deviation of 478.84.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0879088633

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 13606 hours. To test the new design, the company samples 86 of the new lightbulbs, testing their lifespan, and they find a sample mean of 13446.39 and a sample standard deviation of 570.18.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0389202596

Self Assessment 15.6

The average lifespan in a particular country is 68.62 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 91 individuals in this region, recording their lifespans. They find a sample mean of 68.5 and a sample standard deviation of 1.98.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0502837597

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 1 points. To test this, they randomly sample 71 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 0.8 and a sample standard deviation of 3.17.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0638425290

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 47 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 10.2 and a sample standard deviation of 1.98.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0704120031

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 99 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 3.5 and a sample standard deviation of 2.22.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0499630947

The average lifespan in a particular country is 72.55 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 53 individuals in this region, recording their lifespans. They find a sample mean of 73.4 and a sample standard deviation of 1.92.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0965344299

The average lifespan in a particular country is 74.21 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 92 individuals in this region, recording their lifespans. They find a sample mean of 73.8 and a sample standard deviation of 3.67.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0207267451

The average lifespan in a particular country is 77.34 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 38 individuals in this region, recording their lifespans. They find a sample mean of 77.8 and a sample standard deviation of 1.99.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0751215344

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 11 points. A clinical trial was conducted with 92 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 11.6 and a sample standard deviation of 2.6.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0200499761

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 9 points. To test this, they randomly sample 51 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 8.7 and a sample standard deviation of 2.31.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0210649115

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 16 points. A clinical trial was conducted with 48 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 18.1 and a sample standard deviation of 4.41.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0228699148

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 35 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 9.8 and a sample standard deviation of 2.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0400246415

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 5304 hours. To test the new design, the company samples 74 of the new lightbulbs, testing their lifespan, and they find a sample mean of 5345.2 and a sample standard deviation of 169.97.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0356573806

The average lifespan in a particular country is 71.66 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 43 individuals in this region, recording their lifespans. They find a sample mean of 73.4 and a sample standard deviation of 4.24.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0093759868

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 44.17 hours. They randomly sample 96 of the new model phones, testing the battery life, and find a sample mean of 43.4 and a sample standard deviation of 4.28.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0626537597

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 5 points. To test this, they randomly sample 55 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.1 and a sample standard deviation of 1.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0967245255

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 5 points. A clinical trial was conducted with 93 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 4.2 and a sample standard deviation of 7.63.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0266671842

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 10581 hours. To test the new design, the company samples 78 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10620.9 and a sample standard deviation of 315.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0526140157

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 11323 hours. To test the new design, the company samples 58 of the new lightbulbs, testing their lifespan, and they find a sample mean of 11284.5 and a sample standard deviation of 380.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0486622420

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 8 points. To test this, they randomly sample 41 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 7.8 and a sample standard deviation of 1.16.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0507717262

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 7 points. To test this, they randomly sample 83 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 6.9 and a sample standard deviation of 3.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0220978522

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients. To test this, they randomly sample 93 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of -0.1 and a sample standard deviation of 1.23.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0582009912

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 6 points. To test this, they randomly sample 49 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 6.1 and a sample standard deviation of 1.8.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0258394014

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 5046 hours. To test the new design, the company samples 94 of the new lightbulbs, testing their lifespan, and they find a sample mean of 5094.7 and a sample standard deviation of 174.62.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0012332531

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 25.39 hours. They randomly sample 97 of the new model phones, testing the battery life, and find a sample mean of 25.4 and a sample standard deviation of 1.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0853789876

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 6 points. To test this, they randomly sample 97 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 6.2 and a sample standard deviation of 4.76.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0598557069

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3577 hours. To test the new design, the company samples 57 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3609.8 and a sample standard deviation of 102.15.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0086019601

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 2 points. To test this, they randomly sample 95 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 2.5 and a sample standard deviation of 4.45.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0520842146

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 8 points. A clinical trial was conducted with 35 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 8.1 and a sample standard deviation of 1.64.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0894063692

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 51 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 10.8 and a sample standard deviation of 1.98.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0209687681

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 5 points. To test this, they randomly sample 46 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 4.3 and a sample standard deviation of 2.86.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0847890692

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 2331 hours. To test the new design, the company samples 75 of the new lightbulbs, testing their lifespan, and they find a sample mean of 2336.4 and a sample standard deviation of 62.11.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0123607017

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 10 points. To test this, they randomly sample 46 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 11 and a sample standard deviation of 4.2.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0573893777

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 11287 hours. To test the new design, the company samples 48 of the new lightbulbs, testing their lifespan, and they find a sample mean of 11405.7 and a sample standard deviation of 482.71.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0169788216

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 14501 hours. To test the new design, the company samples 58 of the new lightbulbs, testing their lifespan, and they find a sample mean of 14625.2 and a sample standard deviation of 640.26.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0464898176

The average lifespan in a particular country is 75.88 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 70 individuals in this region, recording their lifespans. They find a sample mean of 75.7 and a sample standard deviation of 3.44.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0272997824

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 18.29 hours. They randomly sample 67 of the new model phones, testing the battery life, and find a sample mean of 19 and a sample standard deviation of 4.67.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0833899105

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 39.33 hours. They randomly sample 41 of the new model phones, testing the battery life, and find a sample mean of 40.9 and a sample standard deviation of 4.12.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0994339368

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 96 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 3.8 and a sample standard deviation of 4.78.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0363521404

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 47.75 hours. They randomly sample 81 of the new model phones, testing the battery life, and find a sample mean of 48.7 and a sample standard deviation of 4.48.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0252530749

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 73 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 3.4 and a sample standard deviation of 1.13.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0795726415

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 8207 hours. To test the new design, the company samples 41 of the new lightbulbs, testing their lifespan, and they find a sample mean of 8192.7 and a sample standard deviation of 401.29.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0034412708

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 11225 hours. To test the new design, the company samples 49 of the new lightbulbs, testing their lifespan, and they find a sample mean of 11205.1 and a sample standard deviation of 293.17.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0692646500

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 1 points. To test this, they randomly sample 50 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 1.7 and a sample standard deviation of 3.03.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0661232887

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 9 points. To test this, they randomly sample 58 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 9.1 and a sample standard deviation of 3.45.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0488799215

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 9713 hours. To test the new design, the company samples 43 of the new lightbulbs, testing their lifespan, and they find a sample mean of 9906.1 and a sample standard deviation of 470.66.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0892334092

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 10 points. A clinical trial was conducted with 68 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 11 and a sample standard deviation of 2.51.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0130513511

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 44.51 hours. They randomly sample 65 of the new model phones, testing the battery life, and find a sample mean of 45.2 and a sample standard deviation of 2.67.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0868035440

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 45.86 hours. They randomly sample 52 of the new model phones, testing the battery life, and find a sample mean of 46.1 and a sample standard deviation of 1.53.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0119771290

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 12930 hours. To test the new design, the company samples 46 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12992.4 and a sample standard deviation of 426.39.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0612675982

The average lifespan in a particular country is 66.96 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 53 individuals in this region, recording their lifespans. They find a sample mean of 68 and a sample standard deviation of 2.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0154887636

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 18 points. A clinical trial was conducted with 48 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 18.5 and a sample standard deviation of 3.64.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0961705556

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 8 points. A clinical trial was conducted with 91 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 6.6 and a sample standard deviation of 5.33.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0326943881

The average lifespan in a particular country is 68.93 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 36 individuals in this region, recording their lifespans. They find a sample mean of 71.7 and a sample standard deviation of 4.7.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0463553535

The average lifespan in a particular country is 76.52 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 92 individuals in this region, recording their lifespans. They find a sample mean of 76.8 and a sample standard deviation of 1.84.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0299520108

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 26.58 hours. They randomly sample 80 of the new model phones, testing the battery life, and find a sample mean of 25.8 and a sample standard deviation of 4.57.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0379395027

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 19 points. A clinical trial was conducted with 68 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 20.2 and a sample standard deviation of 4.24.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0272580336

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 5570 hours. To test the new design, the company samples 86 of the new lightbulbs, testing their lifespan, and they find a sample mean of 5598.1 and a sample standard deviation of 224.07.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0040768304

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 10 points. To test this, they randomly sample 97 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 9.9 and a sample standard deviation of 2.82.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0020383617

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients. To test this, they randomly sample 45 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 0.4 and a sample standard deviation of 2.57.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0583755889

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 14684 hours. To test the new design, the company samples 76 of the new lightbulbs, testing their lifespan, and they find a sample mean of 14781.8 and a sample standard deviation of 508.74.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0709463347

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 4 points. To test this, they randomly sample 64 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 3.8 and a sample standard deviation of 1.76.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0480389302

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 25 points. A clinical trial was conducted with 60 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 25.4 and a sample standard deviation of 3.05.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0299357912

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 17 points. A clinical trial was conducted with 39 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 17.5 and a sample standard deviation of 1.44.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0736987861

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 18.27 hours. They randomly sample 45 of the new model phones, testing the battery life, and find a sample mean of 18.4 and a sample standard deviation of 1.92.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0705040170

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 96 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12.2 and a sample standard deviation of 1.11.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0025046427

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 8 points. To test this, they randomly sample 61 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 8 and a sample standard deviation of 2.47.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0087309213

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 27.79 hours. They randomly sample 77 of the new model phones, testing the battery life, and find a sample mean of 27.9 and a sample standard deviation of 4.97.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0986818712

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 3 points. To test this, they randomly sample 48 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 4.1 and a sample standard deviation of 3.38.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0233427864

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 43.60 hours. They randomly sample 52 of the new model phones, testing the battery life, and find a sample mean of 44.4 and a sample standard deviation of 2.27.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0928289459

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 18 points. A clinical trial was conducted with 80 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 17.9 and a sample standard deviation of 3.33.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0844586561

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 1 points. To test this, they randomly sample 79 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 2 and a sample standard deviation of 2.99.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0870577567

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 38 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 10.9 and a sample standard deviation of 3.41.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0370551114

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 9 points. A clinical trial was conducted with 41 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 10.7 and a sample standard deviation of 5.63.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0390745071

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3636 hours. To test the new design, the company samples 64 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3672.7 and a sample standard deviation of 91.52.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0264326001

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 9 points. A clinical trial was conducted with 50 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 9.5 and a sample standard deviation of 4.92.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0336407062

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 14 points. A clinical trial was conducted with 94 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 15.8 and a sample standard deviation of 4.97.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0637389522

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 18 points. A clinical trial was conducted with 67 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 17.4 and a sample standard deviation of 7.65.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0253387196

The average lifespan in a particular country is 65.75 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 66 individuals in this region, recording their lifespans. They find a sample mean of 65.1 and a sample standard deviation of 4.13.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0592450848

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 7375 hours. To test the new design, the company samples 36 of the new lightbulbs, testing their lifespan, and they find a sample mean of 7477.3 and a sample standard deviation of 298.45.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0573180670

The average lifespan in a particular country is 79.15 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 67 individuals in this region, recording their lifespans. They find a sample mean of 80.2 and a sample standard deviation of 4.75.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0819646703

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 34.96 hours. They randomly sample 88 of the new model phones, testing the battery life, and find a sample mean of 35.3 and a sample standard deviation of 2.34.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0397325124

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 37 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.1 and a sample standard deviation of 4.16.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0791239024

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 13732 hours. To test the new design, the company samples 36 of the new lightbulbs, testing their lifespan, and they find a sample mean of 13800.5 and a sample standard deviation of 419.8.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0152029719

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 1 points. To test this, they randomly sample 50 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 1.7 and a sample standard deviation of 3.3.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0871744483

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 4195 hours. To test the new design, the company samples 89 of the new lightbulbs, testing their lifespan, and they find a sample mean of 4236.7 and a sample standard deviation of 106.66.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0104543401

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 19 points. A clinical trial was conducted with 80 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 18.9 and a sample standard deviation of 5.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0411322863

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 7 points. To test this, they randomly sample 86 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 7.5 and a sample standard deviation of 4.76.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0620079253

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 2 points. To test this, they randomly sample 60 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 1.5 and a sample standard deviation of 3.73.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0223058847

The average lifespan in a particular country is 73.77 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 96 individuals in this region, recording their lifespans. They find a sample mean of 73.9 and a sample standard deviation of 1.4.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0629144876

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 10 points. To test this, they randomly sample 84 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 9.9 and a sample standard deviation of 1.61.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0010739284

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 86 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12.4 and a sample standard deviation of 2.05.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0056351915

The average lifespan in a particular country is 68.52 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 77 individuals in this region, recording their lifespans. They find a sample mean of 68.7 and a sample standard deviation of 1.29.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0893197254

The average lifespan in a particular country is 71.33 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 68 individuals in this region, recording their lifespans. They find a sample mean of 71.2 and a sample standard deviation of 1.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0016026710

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 6414 hours. To test the new design, the company samples 62 of the new lightbulbs, testing their lifespan, and they find a sample mean of 6484.1 and a sample standard deviation of 267.31.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0860893801

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 23 points. A clinical trial was conducted with 68 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 23.4 and a sample standard deviation of 6.06.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0313781002

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 65 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12 and a sample standard deviation of 1.33.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0756502444

The average lifespan in a particular country is 78.1 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 71 individuals in this region, recording their lifespans. They find a sample mean of 78.4 and a sample standard deviation of 1.25.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0289671376

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 7103 hours. To test the new design, the company samples 47 of the new lightbulbs, testing their lifespan, and they find a sample mean of 7072.4 and a sample standard deviation of 200.53.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0290556255

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 23.34 hours. They randomly sample 62 of the new model phones, testing the battery life, and find a sample mean of 24.5 and a sample standard deviation of 4.54.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0676352313

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 25 points. A clinical trial was conducted with 59 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 26.2 and a sample standard deviation of 6.02.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value calculated when running this hypothesis test?
3. What is the conclusion from the hypothesis test, if \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0285942279

Self Assessment 15.7

A factory that fills food containers has a process that is meant to fill individual boxes to 469 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 96 boxes, weighing them. They find a sample mean of 469.4 and a sample standard deviation of 9.01.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0870819604

A factory that fills food containers has a process that is meant to fill individual boxes to 593 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 54 boxes, weighing them. They find a sample mean of 594.2 and a sample standard deviation of 7.88.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0093012077

A large chain coffee shop claims that their lattes have 151 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 63 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 149.2 and a sample standard deviation of 4.85.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0459485291

A factory that fills food containers has a process that is meant to fill individual boxes to 501 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 100 boxes, weighing them. They find a sample mean of 500.1 and a sample standard deviation of 5.19.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0552628739

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 141.2 . To understand the impact of the diet, they randomly select 71 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 142.5 and a sample standard deviation of 12.62.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0041352399

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 80 . To test the new method, they randomly sample 39 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 81.2 and a sample standard deviation of 7.45.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0992246239

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.3108 seconds. The researchers randomly sample 39 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.2 and a sample standard deviation of 0.0904.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0640331712

A factory that fills food containers has a process that is meant to fill individual boxes to 575 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 81 boxes, weighing them. They find a sample mean of 573.9 and a sample standard deviation of 7.85.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0229709726

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 168.2 . To understand the impact of the diet, they randomly select 52 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 170 and a sample standard deviation of 11.33.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0187218020

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.4459 seconds. The researchers randomly sample 100 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0865.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0932539304

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6394 seconds. The researchers randomly sample 80 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.0981.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0920546205

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6663 seconds. The researchers randomly sample 45 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0552.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0009018706

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 138 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 91 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 138.9 and a sample standard deviation of 22.93.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0775292068

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 108 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 87 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 106.4 and a sample standard deviation of 20.46.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0924769329

A large chain coffee shop claims that their lattes have 158 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 55 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 158.6 and a sample standard deviation of 2.04.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0522189205

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 177.73 . To understand the impact of the diet, they randomly select 37 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 180.2 and a sample standard deviation of 14.61.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0044931678

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.4218 seconds. The researchers randomly sample 67 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0788.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0276608319

A large chain coffee shop claims that their lattes have 146 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 94 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 144.5 and a sample standard deviation of 3.8.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0356340430

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.5670 seconds. The researchers randomly sample 85 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.0845.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0580730676

A factory that fills food containers has a process that is meant to fill individual boxes to 591 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 42 boxes, weighing them. They find a sample mean of 588.5 and a sample standard deviation of 9.99.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0014853520

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 55 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 67 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 55.6 and a sample standard deviation of 9.53.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202896137

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 53 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 82 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 58.7 and a sample standard deviation of 22.39.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0088040260

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 176.86 . To understand the impact of the diet, they randomly select 52 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 181.8 and a sample standard deviation of 13.39.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0049471860

A factory that fills food containers has a process that is meant to fill individual boxes to 462 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 52 boxes, weighing them. They find a sample mean of 458.5 and a sample standard deviation of 7.7.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0183720015

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 169.28 . To understand the impact of the diet, they randomly select 99 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 170.2 and a sample standard deviation of 10.42.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0346464873

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 80 . To test the new method, they randomly sample 46 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 82.8 and a sample standard deviation of 7.63.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0303861118

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.2686 seconds. The researchers randomly sample 98 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.3 and a sample standard deviation of 0.0899.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0438600072

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6303 seconds. The researchers randomly sample 58 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.074.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0010577105

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 73 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 43 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 78.8 and a sample standard deviation of 10.67.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0969429721

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 151.34 . To understand the impact of the diet, they randomly select 72 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 151.9 and a sample standard deviation of 5.58.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0287774724

A large chain coffee shop claims that their lattes have 145 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 46 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 144.9 and a sample standard deviation of 2.81.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0626691191

A factory that fills food containers has a process that is meant to fill individual boxes to 503 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 97 boxes, weighing them. They find a sample mean of 503.9 and a sample standard deviation of 9.47.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0334851401

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.3600 seconds. The researchers randomly sample 64 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.3 and a sample standard deviation of 0.0895.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0541769305

A factory that fills food containers has a process that is meant to fill individual boxes to 447 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 62 boxes, weighing them. They find a sample mean of 450.9 and a sample standard deviation of 9.9.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0330549111

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 91 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 41 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 89.7 and a sample standard deviation of 7.28.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0853993777

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.5749 seconds. The researchers randomly sample 39 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.6 and a sample standard deviation of 0.0904.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0370595134

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.4037 seconds. The researchers randomly sample 54 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0949.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0787934002

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.5460 seconds. The researchers randomly sample 40 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0815.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0096350974

A large chain coffee shop claims that their lattes have 147 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 97 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 147.3 and a sample standard deviation of 4.99.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0751556973

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 73 . To test the new method, they randomly sample 98 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 75 and a sample standard deviation of 6.94.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0829376377

A large chain coffee shop claims that their lattes have 152 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 36 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 151.9 and a sample standard deviation of 2.06.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0101955513

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 172 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 49 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 167.4 and a sample standard deviation of 10.41.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0913974270

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6326 seconds. The researchers randomly sample 43 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0511.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0576975777

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 162 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 43 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 165.9 and a sample standard deviation of 20.43.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0672222879

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 167.75 . To understand the impact of the diet, they randomly select 46 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 169.4 and a sample standard deviation of 11.27.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0984783370

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 153.46 . To understand the impact of the diet, they randomly select 80 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 157.1 and a sample standard deviation of 12.97.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0884241055

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6856 seconds. The researchers randomly sample 64 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0746.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0301085814

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 41 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 78.6 and a sample standard deviation of 6.05.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0072001399

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 178 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 56 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 173.7 and a sample standard deviation of 14.67.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0305927023

A large chain coffee shop claims that their lattes have 150 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 58 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 150.2 and a sample standard deviation of 2.57.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0713852132

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 70 . To test the new method, they randomly sample 80 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 72 and a sample standard deviation of 8.45.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0911279478

A large chain coffee shop claims that their lattes have 157 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 74 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 157.3 and a sample standard deviation of 2.34.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0898136480

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 140.23 . To understand the impact of the diet, they randomly select 35 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 141.8 and a sample standard deviation of 10.29.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0438993022

A large chain coffee shop claims that their lattes have 145 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 76 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 143.9 and a sample standard deviation of 3.24.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0593338211

A factory that fills food containers has a process that is meant to fill individual boxes to 438 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 61 boxes, weighing them. They find a sample mean of 438.8 and a sample standard deviation of 9.16.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0103478029

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 161.79 . To understand the impact of the diet, they randomly select 74 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 158.1 and a sample standard deviation of 14.31.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0449500306

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6720 seconds. The researchers randomly sample 68 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0882.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0919873187

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 72 . To test the new method, they randomly sample 73 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 70.9 and a sample standard deviation of 9.28.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0501018050

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.2833 seconds. The researchers randomly sample 92 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.3 and a sample standard deviation of 0.0694.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0067138058

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 161 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 42 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 160.2 and a sample standard deviation of 3.39.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0361961607

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 61 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 65 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 63.3 and a sample standard deviation of 19.37.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0442952125

A factory that fills food containers has a process that is meant to fill individual boxes to 538 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 99 boxes, weighing them. They find a sample mean of 538.9 and a sample standard deviation of 8.84.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0094257600

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 148.1 . To understand the impact of the diet, they randomly select 63 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 147.2 and a sample standard deviation of 11.32.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0157107631

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.3374 seconds. The researchers randomly sample 79 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.3 and a sample standard deviation of 0.0593.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0621267234

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 78 . To test the new method, they randomly sample 65 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 81.2 and a sample standard deviation of 7.36.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0301720681

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 88 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 52 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 93.4 and a sample standard deviation of 16.5.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0555602088

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 169 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 95 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 162.6 and a sample standard deviation of 22.65.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0085862796

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.6494 seconds. The researchers randomly sample 97 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0873.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0749620079

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 76 . To test the new method, they randomly sample 93 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 76.7 and a sample standard deviation of 7.94.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0599375751

A large chain coffee shop claims that their lattes have 159 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 45 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 158.6 and a sample standard deviation of 2.85.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0782380219

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 148.72 . To understand the impact of the diet, they randomly select 88 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 150.2 and a sample standard deviation of 9.17.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0314644239

A factory that fills food containers has a process that is meant to fill individual boxes to 536 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 41 boxes, weighing them. They find a sample mean of 531.9 and a sample standard deviation of 9.46.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0733584530

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 106 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 66 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 101.9 and a sample standard deviation of 12.79.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0595204315

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.3535 seconds. The researchers randomly sample 95 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.3 and a sample standard deviation of 0.0901.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0774434876

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 140.91 . To understand the impact of the diet, they randomly select 70 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 142 and a sample standard deviation of 12.96.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0248367018

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 76 . To test the new method, they randomly sample 43 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 76.7 and a sample standard deviation of 9.49.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0798563701

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 75 . To test the new method, they randomly sample 72 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 73.6 and a sample standard deviation of 7.43.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0613694106

A factory that fills food containers has a process that is meant to fill individual boxes to 531 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 60 boxes, weighing them. They find a sample mean of 532 and a sample standard deviation of 7.83.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0670442912

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 154.16 . To understand the impact of the diet, they randomly select 70 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 158.6 and a sample standard deviation of 11.46.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0095903562

A factory that fills food containers has a process that is meant to fill individual boxes to 406 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 62 boxes, weighing them. They find a sample mean of 404 and a sample standard deviation of 5.82.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0182373872

A large chain coffee shop claims that their lattes have 141 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 54 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 142.8 and a sample standard deviation of 4.84.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0823156007

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.7341 seconds. The researchers randomly sample 38 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0898.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202872978

A factory that fills food containers has a process that is meant to fill individual boxes to 461 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 79 boxes, weighing them. They find a sample mean of 458.3 and a sample standard deviation of 5.33.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0843788594

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 169.6 . To understand the impact of the diet, they randomly select 81 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 166.7 and a sample standard deviation of 11.61.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0865672202

A large chain coffee shop claims that their lattes have 141 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 69 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 141.8 and a sample standard deviation of 2.19.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0468048639

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.5338 seconds. The researchers randomly sample 73 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0531.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0479215901

A teacher is investigating the impact of a new teaching method for their students. Historically, the standardized test used to assess the students has had students scoring an average of 75 . To test the new method, they randomly sample 85 students to be given the new teaching method. They record the standardized test scores for each individual. They find a sample mean of 71.9 and a sample standard deviation of 8.5.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0561050019

A biologist is studying the average lifespan of a particular species of beetle. Based on previous research, the average lifespan of these beetles is known to be 100 days. The biologist suspects that environmental changes in a specific region might be affecting the beetles’ lifespan. They observe a sample of 46 beetles from the specific region, measuring the lifepsan of these sampled beetles. They find a sample mean of 102.7 and a sample standard deviation of 9.67.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0292549335

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 153.77 . To understand the impact of the diet, they randomly select 69 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 156.2 and a sample standard deviation of 11.81.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0175551467

A large chain coffee shop claims that their lattes have 158 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 83 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 157.4 and a sample standard deviation of 2.61.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0553085930

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.7082 seconds. The researchers randomly sample 93 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.7 and a sample standard deviation of 0.0815.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0652800698

A large chain coffee shop claims that their lattes have 140 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 69 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 140.3 and a sample standard deviation of 3.07.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0459044059

A large chain coffee shop claims that their lattes have 140 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 76 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 141.4 and a sample standard deviation of 4.25.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0835253372

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.3473 seconds. The researchers randomly sample 69 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0739.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0041033527

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.4963 seconds. The researchers randomly sample 95 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.5 and a sample standard deviation of 0.0813.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0299955393

A factory that fills food containers has a process that is meant to fill individual boxes to 444 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 90 boxes, weighing them. They find a sample mean of 447.6 and a sample standard deviation of 8.05.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0328991168

A medical researcher is interested in understanding if a particular diet has an impact on individual blood pressure. In the population they know the average blood pressure is 162.88 . To understand the impact of the diet, they randomly select 53 individuals, and have them change their diet. Following up, the research records each individual’s blood pressure. They find a sample mean of 160.3 and a sample standard deviation of 5.37.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0155406093

A researcher is studying the impact of a particular drug on human reaction times. They know that the average reaction time for subjects without the drug in the task is 0.4593 seconds. The researchers randomly sample 64 individuals, providing them the drug, and measure their reaction times. They find a sample mean of 0.4 and a sample standard deviation of 0.0966.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0678568516

A factory that fills food containers has a process that is meant to fill individual boxes to 503 g. To ensure that the process has not resulted in faulty calibration, the company randomly samples 47 boxes, weighing them. They find a sample mean of 500.8 and a sample standard deviation of 7.62.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0530645060

A large chain coffee shop claims that their lattes have 141 mg of caffeine. A researcher, who stops to grab a latte from this chain each morning, is curious as to whether this claim is accurate. As a result, they purchase a sample of 43 lattes, randomly from various locations, and bring them to a lab to measure the caffeine content. Doing this they find a sample mean of 139.3 and a sample standard deviation of 2.85.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0464894295

Self Assessment 15.8

A cloud server host is contractually obligated to maintain a server load time of no more than 185.20 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 99 page visits, recording the load time for each, and find a sample mean of 176.89 and a sample standard deviation of 83.4.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0234522880

A coffee shop chain claims that their average cup of coffee contains 12.15 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.15 ounces. They randomly sample 94 cups of coffee from various locations and find a sample mean of 12.2 and a sample standard deviation of 0.3.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0357652468

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 10614 hours. To test their competitor’s new design, the company purchases 56 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10570.73 and a sample standard deviation of 287.47.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0728726086

A cloud server host is contractually obligated to maintain a server load time of no more than 221.17 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 95 page visits, recording the load time for each, and find a sample mean of 224.78 and a sample standard deviation of 40.4.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0936343865

A coffee shop chain claims that their average cup of coffee contains 10.25 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.25 ounces. They randomly sample 65 cups of coffee from various locations and find a sample mean of 10.26 and a sample standard deviation of 0.34.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0628835508

A phone manufacturer claims that their phone batteries last for an average of 35.17 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 37 phones, testing the battery life, and find a sample mean of 34.01 and a sample standard deviation of 2.82.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0755724453

A phone manufacturer claims that their phone batteries last for an average of 16.21 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 92 phones, testing the battery life, and find a sample mean of 16.05 and a sample standard deviation of 2.73.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0953208981

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 158.04 . To test its efficacy, researchers take a sample of 63 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 159.19 and a sample standard deviation of 12.13.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0170167681

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 11009 hours. To test their competitor’s new design, the company purchases 82 of the new lightbulbs, testing their lifespan, and they find a sample mean of 11027.17 and a sample standard deviation of 455.38.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0826446093

A phone manufacturer claims that their phone batteries last for an average of 17.56 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 53 phones, testing the battery life, and find a sample mean of 17.71 and a sample standard deviation of 1.09.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0005551235

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 172.96 . To test its efficacy, researchers take a sample of 100 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 171.82 and a sample standard deviation of 6.29.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0423297352

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 4156 hours. To test their competitor’s new design, the company purchases 60 of the new lightbulbs, testing their lifespan, and they find a sample mean of 4148.89 and a sample standard deviation of 132.84.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0950326809

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.68 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 77 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 5.65 and a sample standard deviation of 1.81.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0060983664

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 179.09 . To test its efficacy, researchers take a sample of 80 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 175.76 and a sample standard deviation of 11.67.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0007885585

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 162.88 . To test its efficacy, researchers take a sample of 53 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 161.01 and a sample standard deviation of 8.82.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0583256084

A cloud server host is contractually obligated to maintain a server load time of no more than 101.57 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 75 page visits, recording the load time for each, and find a sample mean of 96.45 and a sample standard deviation of 49.58.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0776527498

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 11.12 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 46 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 11.52 and a sample standard deviation of 2.82.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0676258231

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 143.05 . To test its efficacy, researchers take a sample of 74 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 143.67 and a sample standard deviation of 12.95.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0746215122

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 8.36 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 48 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 8.8 and a sample standard deviation of 2.65.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0255201743

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 6.87 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 46 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 6.54 and a sample standard deviation of 1.2.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0255254415

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 14.74 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 65 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 15.32 and a sample standard deviation of 2.74.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0680057539

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 14082 hours. To test their competitor’s new design, the company purchases 90 of the new lightbulbs, testing their lifespan, and they find a sample mean of 13967.3 and a sample standard deviation of 505.11.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0872528833

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 6730 hours. To test their competitor’s new design, the company purchases 72 of the new lightbulbs, testing their lifespan, and they find a sample mean of 6657.36 and a sample standard deviation of 280.5.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0101003829

A coffee shop chain claims that their average cup of coffee contains 10.61 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.61 ounces. They randomly sample 37 cups of coffee from various locations and find a sample mean of 10.56 and a sample standard deviation of 1.07.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0402408757

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.34 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 44 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 11.19 and a sample standard deviation of 4.32.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0568889139

A phone manufacturer claims that their phone batteries last for an average of 18.62 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 86 phones, testing the battery life, and find a sample mean of 18.46 and a sample standard deviation of 2.25.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0939975193

A cloud server host is contractually obligated to maintain a server load time of no more than 437.70 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 88 page visits, recording the load time for each, and find a sample mean of 392.01 and a sample standard deviation of 163.16.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0882708541

A cloud server host is contractually obligated to maintain a server load time of no more than 269.14 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 96 page visits, recording the load time for each, and find a sample mean of 256 and a sample standard deviation of 70.05.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0599390699

A phone manufacturer claims that their phone batteries last for an average of 16.31 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 65 phones, testing the battery life, and find a sample mean of 15.11 and a sample standard deviation of 4.12.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0288772697

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 7.95 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 85 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 8.08 and a sample standard deviation of 2.56.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0113295105

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.59 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 81 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 14.24 and a sample standard deviation of 4.39.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0715501561

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 165.31 . To test its efficacy, researchers take a sample of 82 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 162.49 and a sample standard deviation of 14.67.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0609262709

A coffee shop chain claims that their average cup of coffee contains 12.20 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.20 ounces. They randomly sample 93 cups of coffee from various locations and find a sample mean of 12.1 and a sample standard deviation of 0.29.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0602588211

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 157.43 . To test its efficacy, researchers take a sample of 95 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 155.44 and a sample standard deviation of 12.74.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0916121281

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 12905 hours. To test their competitor’s new design, the company purchases 44 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12888.08 and a sample standard deviation of 485.22.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0064944545

A cloud server host is contractually obligated to maintain a server load time of no more than 366.53 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 93 page visits, recording the load time for each, and find a sample mean of 387.33 and a sample standard deviation of 178.95.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202095044

A coffee shop chain claims that their average cup of coffee contains 10.96 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.96 ounces. They randomly sample 36 cups of coffee from various locations and find a sample mean of 10.33 and a sample standard deviation of 1.5.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0681898617

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 3.10 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 38 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 2.85 and a sample standard deviation of 0.76.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0183249722

A phone manufacturer claims that their phone batteries last for an average of 26.33 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 68 phones, testing the battery life, and find a sample mean of 25.32 and a sample standard deviation of 3.58.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0387754280

A phone manufacturer claims that their phone batteries last for an average of 19.15 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 35 phones, testing the battery life, and find a sample mean of 17.81 and a sample standard deviation of 4.05.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0706607090

A phone manufacturer claims that their phone batteries last for an average of 40.21 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 39 phones, testing the battery life, and find a sample mean of 40.93 and a sample standard deviation of 3.71.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0203207873

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 7.83 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 73 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 7.71 and a sample standard deviation of 1.61.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0674874892

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 6547 hours. To test their competitor’s new design, the company purchases 59 of the new lightbulbs, testing their lifespan, and they find a sample mean of 6509.8 and a sample standard deviation of 243.34.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0300620098

A phone manufacturer claims that their phone batteries last for an average of 41.12 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 43 phones, testing the battery life, and find a sample mean of 41.18 and a sample standard deviation of 1.55.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0168234297

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 9575 hours. To test their competitor’s new design, the company purchases 71 of the new lightbulbs, testing their lifespan, and they find a sample mean of 9575.34 and a sample standard deviation of 317.41.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0445617384

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.72 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 69 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 14.07 and a sample standard deviation of 3.47.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0099063203

A phone manufacturer claims that their phone batteries last for an average of 28.05 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 36 phones, testing the battery life, and find a sample mean of 27.45 and a sample standard deviation of 2.33.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.2\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0555351841

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 3894 hours. To test their competitor’s new design, the company purchases 76 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3913.89 and a sample standard deviation of 120.32.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0075055094

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 177.47 . To test its efficacy, researchers take a sample of 94 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 178.01 and a sample standard deviation of 12.21.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0353127170

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 14176 hours. To test their competitor’s new design, the company purchases 37 of the new lightbulbs, testing their lifespan, and they find a sample mean of 14154.93 and a sample standard deviation of 389.2.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0787210933

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 12108 hours. To test their competitor’s new design, the company purchases 94 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12000.39 and a sample standard deviation of 583.03.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0656673237

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 149.74 . To test its efficacy, researchers take a sample of 70 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 145.65 and a sample standard deviation of 10.66.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0164143574

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 161.91 . To test its efficacy, researchers take a sample of 90 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 160.06 and a sample standard deviation of 10.52.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0648668817

A cloud server host is contractually obligated to maintain a server load time of no more than 241.68 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 99 page visits, recording the load time for each, and find a sample mean of 265.59 and a sample standard deviation of 98.59.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0267578625

A cloud server host is contractually obligated to maintain a server load time of no more than 321.76 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 46 page visits, recording the load time for each, and find a sample mean of 263.7 and a sample standard deviation of 160.83.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0771727665

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.29 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 92 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 12.77 and a sample standard deviation of 2.78.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0902321119

A coffee shop chain claims that their average cup of coffee contains 11.90 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 11.90 ounces. They randomly sample 62 cups of coffee from various locations and find a sample mean of 11.78 and a sample standard deviation of 0.48.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0485773579

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 156.19 . To test its efficacy, researchers take a sample of 52 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 155.95 and a sample standard deviation of 9.54.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0788148487

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 160.94 . To test its efficacy, researchers take a sample of 93 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 163.03 and a sample standard deviation of 13.18.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0205277145

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 168.84 . To test its efficacy, researchers take a sample of 41 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 160.75 and a sample standard deviation of 14.78.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0479449968

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.63 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 88 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 5.84 and a sample standard deviation of 1.39.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0808784303

A phone manufacturer claims that their phone batteries last for an average of 36.25 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 96 phones, testing the battery life, and find a sample mean of 35.66 and a sample standard deviation of 3.07.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0087543992

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 172.62 . To test its efficacy, researchers take a sample of 90 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 172.49 and a sample standard deviation of 10.54.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0586569308

A cloud server host is contractually obligated to maintain a server load time of no more than 398.29 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 77 page visits, recording the load time for each, and find a sample mean of 374.93 and a sample standard deviation of 142.26.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0120545680

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 10.05 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 85 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 10.17 and a sample standard deviation of 1.95.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0944778740

A cloud server host is contractually obligated to maintain a server load time of no more than 203.41 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 80 page visits, recording the load time for each, and find a sample mean of 219.13 and a sample standard deviation of 65.03.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0370481360

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 13.35 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 52 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 13.77 and a sample standard deviation of 3.75.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0829574641

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 175.89 . To test its efficacy, researchers take a sample of 47 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 175.9 and a sample standard deviation of 11.34.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0791686224

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.11 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 91 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 5.01 and a sample standard deviation of 1.54.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0059045963

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 140.10 . To test its efficacy, researchers take a sample of 68 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 140.26 and a sample standard deviation of 11.14.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0057766873

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 14.74 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 50 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 13.69 and a sample standard deviation of 3.7.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0843419292

A cloud server host is contractually obligated to maintain a server load time of no more than 242.24 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 79 page visits, recording the load time for each, and find a sample mean of 222.17 and a sample standard deviation of 87.25.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0916128571

A cloud server host is contractually obligated to maintain a server load time of no more than 244.95 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 81 page visits, recording the load time for each, and find a sample mean of 250.75 and a sample standard deviation of 54.35.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0230509828

A coffee shop chain claims that their average cup of coffee contains 13.06 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 13.06 ounces. They randomly sample 44 cups of coffee from various locations and find a sample mean of 12.84 and a sample standard deviation of 1.28.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0514090044

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.46 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 37 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.95 and a sample standard deviation of 1.52.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0754418870

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 6.92 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 38 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 6.16 and a sample standard deviation of 2.02.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0843118669

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 3.60 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 62 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 3.41 and a sample standard deviation of 0.79.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0826781513

A cloud server host is contractually obligated to maintain a server load time of no more than 80.95 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 63 page visits, recording the load time for each, and find a sample mean of 85.45 and a sample standard deviation of 30.09.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0738843969

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 9408 hours. To test their competitor’s new design, the company purchases 42 of the new lightbulbs, testing their lifespan, and they find a sample mean of 9433.43 and a sample standard deviation of 412.71.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0539648689

A phone manufacturer claims that their phone batteries last for an average of 35.62 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 66 phones, testing the battery life, and find a sample mean of 35.6 and a sample standard deviation of 4.86.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0521481264

A coffee shop chain claims that their average cup of coffee contains 10.53 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.53 ounces. They randomly sample 90 cups of coffee from various locations and find a sample mean of 10.15 and a sample standard deviation of 1.05.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0653155256

A cloud server host is contractually obligated to maintain a server load time of no more than 498.66 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 61 page visits, recording the load time for each, and find a sample mean of 544.38 and a sample standard deviation of 182.67.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0247992687

A cloud server host is contractually obligated to maintain a server load time of no more than 153.13 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 42 page visits, recording the load time for each, and find a sample mean of 139.39 and a sample standard deviation of 61.78.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0094418394

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 157.83 . To test its efficacy, researchers take a sample of 51 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 158.68 and a sample standard deviation of 8.01.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0117281547

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 4830 hours. To test their competitor’s new design, the company purchases 69 of the new lightbulbs, testing their lifespan, and they find a sample mean of 4889.19 and a sample standard deviation of 232.81.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0848004365

A phone manufacturer claims that their phone batteries last for an average of 44.96 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 43 phones, testing the battery life, and find a sample mean of 43.45 and a sample standard deviation of 4.94.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0885850102

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.44 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 72 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 5.22 and a sample standard deviation of 1.27.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0869446996

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 5.08 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 61 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 4.83 and a sample standard deviation of 1.08.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0377841333

A vehicle manufacturer claims that their vehicles achieve an average fuel efficiency of 6.80 L/100km. A consumer magazine suspects that this is being overestimated. They randomly sample 98 of these vehicles, and record the fuel efficiency of each, finding a sample mean of 6.39 and a sample standard deviation of 2.11.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0698042823

A coffee shop chain claims that their average cup of coffee contains 10.09 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 10.09 ounces. They randomly sample 40 cups of coffee from various locations and find a sample mean of 9.69 and a sample standard deviation of 1.27.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0450227262

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 12762 hours. To test their competitor’s new design, the company purchases 52 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12790.75 and a sample standard deviation of 430.02.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0823206343

A lightbulb manufacturer suspects that a competitor’s new design has a shorter lifespan than their existing design. Their existing design is rated for an average of 8819 hours. To test their competitor’s new design, the company purchases 88 of the new lightbulbs, testing their lifespan, and they find a sample mean of 8793.93 and a sample standard deviation of 392.68.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0252874078

A cloud server host is contractually obligated to maintain a server load time of no more than 152.36 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 87 page visits, recording the load time for each, and find a sample mean of 136.04 and a sample standard deviation of 54.7.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0916651591

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 168.93 . To test its efficacy, researchers take a sample of 49 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 168.16 and a sample standard deviation of 5.01.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0859917232

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 143.37 . To test its efficacy, researchers take a sample of 60 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 143.97 and a sample standard deviation of 7.38.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0705938759

A coffee shop chain claims that their average cup of coffee contains 12.38 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 12.38 ounces. They randomly sample 74 cups of coffee from various locations and find a sample mean of 12.53 and a sample standard deviation of 0.83.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0241601216

A phone manufacturer claims that their phone batteries last for an average of 45.29 hours. A tech YouTuber suspects that this is an overstatement, and wish to use statistical techniques to demonstrate their claim. They purchase 42 phones, testing the battery life, and find a sample mean of 45.42 and a sample standard deviation of 2.73.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0716278658

A cloud server host is contractually obligated to maintain a server load time of no more than 475.99 milliseconds. A data analyst working with quality assurance is responsible for providing statistical evidence as to whether this is achieved. They randomly sample 82 page visits, recording the load time for each, and find a sample mean of 450.87 and a sample standard deviation of 209.62.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0012025756

A coffee shop chain claims that their average cup of coffee contains 13.47 ounces of coffee. A consumer advocacy group suspects that the actual average amount is less than 13.47 ounces. They randomly sample 47 cups of coffee from various locations and find a sample mean of 13.29 and a sample standard deviation of 1.19.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0780401144

A new drug is developed to lower the blood pressure of members of a particular population. The population average is 162.61 . To test its efficacy, researchers take a sample of 81 individuals from the population, prescribe them the medication, and then monitor their blood pressure. Doing this they find a sample mean of 164.25 and a sample standard deviation of 14.56.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0807976680

Self Assessment 15.9

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 22.86 hours. They randomly sample 51 of the new model phones, testing the battery life, and find a sample mean of 24.5 and a sample standard deviation of 4.15.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0047126685

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 9 points. To test this, they randomly sample 58 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 9 and a sample standard deviation of 1.15.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0176754532

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 23 points. A clinical trial was conducted with 46 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 26.9 and a sample standard deviation of 7.78.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0015981230

The average lifespan in a particular country is 72.12 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 70 individuals in this region, recording their lifespans. They find a sample mean of 71.8 and a sample standard deviation of 2.37.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0258765183

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 10 points. To test this, they randomly sample 57 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 10.2 and a sample standard deviation of 1.32.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0712213897

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 10 points. A clinical trial was conducted with 90 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 11.5 and a sample standard deviation of 5.16.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0380685190

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 41.34 hours. They randomly sample 87 of the new model phones, testing the battery life, and find a sample mean of 42.5 and a sample standard deviation of 3.61.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0080087710

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 46.51 hours. They randomly sample 71 of the new model phones, testing the battery life, and find a sample mean of 48 and a sample standard deviation of 4.8.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0821820073

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 9 points. To test this, they randomly sample 57 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 9.4 and a sample standard deviation of 2.13.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0274633184

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3337 hours. To test the new design, the company samples 83 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3348 and a sample standard deviation of 88.61.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0084584496

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 41.78 hours. They randomly sample 53 of the new model phones, testing the battery life, and find a sample mean of 42 and a sample standard deviation of 1.03.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0630819826

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 8 points. A clinical trial was conducted with 71 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 7 and a sample standard deviation of 5.11.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0622490233

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 7975 hours. To test the new design, the company samples 98 of the new lightbulbs, testing their lifespan, and they find a sample mean of 8010 and a sample standard deviation of 284.98.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0249231818

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 30.89 hours. They randomly sample 81 of the new model phones, testing the battery life, and find a sample mean of 31.8 and a sample standard deviation of 4.98.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0970630370

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3043 hours. To test the new design, the company samples 58 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3030.8 and a sample standard deviation of 84.75.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0001947816

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 20 points. A clinical trial was conducted with 94 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 21.2 and a sample standard deviation of 7.3.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0456068967

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 8 points. To test this, they randomly sample 80 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 9 and a sample standard deviation of 4.2.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0681342780

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 1 points. To test this, they randomly sample 55 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 0.7 and a sample standard deviation of 1.67.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0218858641

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 12153 hours. To test the new design, the company samples 59 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12291 and a sample standard deviation of 313.26.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0021591611

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 73 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 10.1 and a sample standard deviation of 1.79.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0684160689

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients. To test this, they randomly sample 89 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 0.8 and a sample standard deviation of 1.71.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0054383964

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 15.63 hours. They randomly sample 69 of the new model phones, testing the battery life, and find a sample mean of 15.6 and a sample standard deviation of 1.32.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0442886609

The average lifespan in a particular country is 68.99 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 56 individuals in this region, recording their lifespans. They find a sample mean of 69.8 and a sample standard deviation of 4.72.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0668124192

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 25 points. A clinical trial was conducted with 42 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 24.2 and a sample standard deviation of 3.62.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0245919215

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 6 points. To test this, they randomly sample 70 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 6.6 and a sample standard deviation of 2.99.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0062372803

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 9 points. To test this, they randomly sample 40 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 10.5 and a sample standard deviation of 3.37.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0421865219

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 10 points. To test this, they randomly sample 68 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 10.2 and a sample standard deviation of 4.65.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0097137725

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 3383 hours. To test the new design, the company samples 57 of the new lightbulbs, testing their lifespan, and they find a sample mean of 3382.5 and a sample standard deviation of 122.02.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0681707448

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 8 points. A clinical trial was conducted with 69 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 8.8 and a sample standard deviation of 4.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0240886109

The average lifespan in a particular country is 66.89 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 69 individuals in this region, recording their lifespans. They find a sample mean of 68.2 and a sample standard deviation of 3.36.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0485067911

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 18.86 hours. They randomly sample 74 of the new model phones, testing the battery life, and find a sample mean of 19.5 and a sample standard deviation of 3.01.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0725280566

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 19.70 hours. They randomly sample 37 of the new model phones, testing the battery life, and find a sample mean of 19.5 and a sample standard deviation of 1.34.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0188059103

The average lifespan in a particular country is 75.89 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 86 individuals in this region, recording their lifespans. They find a sample mean of 75.4 and a sample standard deviation of 3.64.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0682787016

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 6 points. To test this, they randomly sample 72 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.7 and a sample standard deviation of 4.61.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0988706739

The average lifespan in a particular country is 73.32 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 88 individuals in this region, recording their lifespans. They find a sample mean of 73.5 and a sample standard deviation of 1.15.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0572668462

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 3 points. To test this, they randomly sample 80 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 4.1 and a sample standard deviation of 3.52.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0942744976

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients. To test this, they randomly sample 58 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 0.4 and a sample standard deviation of 2.16.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0898704124

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 3 points. To test this, they randomly sample 68 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 4.2 and a sample standard deviation of 3.25.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0287325174

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 10 points. A clinical trial was conducted with 73 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 10.6 and a sample standard deviation of 4.9.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0427377603

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 63 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12 and a sample standard deviation of 2.09.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0887033898

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 4 points. To test this, they randomly sample 71 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 4.5 and a sample standard deviation of 2.19.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0225610391

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 23.26 hours. They randomly sample 50 of the new model phones, testing the battery life, and find a sample mean of 24.3 and a sample standard deviation of 3.24.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0789719476

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 5 points. To test this, they randomly sample 91 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 4.9 and a sample standard deviation of 2.64.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0584923138

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 12894 hours. To test the new design, the company samples 100 of the new lightbulbs, testing their lifespan, and they find a sample mean of 12982.4 and a sample standard deviation of 615.16.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0503538978

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 6 points. To test this, they randomly sample 87 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.4 and a sample standard deviation of 3.79.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0913971955

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 18 points. A clinical trial was conducted with 88 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 18.4 and a sample standard deviation of 3.93.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0318898901

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 8 points. To test this, they randomly sample 100 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 7.9 and a sample standard deviation of 3.03.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202692135

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 37 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 2.7 and a sample standard deviation of 2.89.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0693887336

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 21 points. A clinical trial was conducted with 79 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 21 and a sample standard deviation of 2.05.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0367446278

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 6 points. To test this, they randomly sample 50 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 6.4 and a sample standard deviation of 1.76.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0033634581

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 5018 hours. To test the new design, the company samples 49 of the new lightbulbs, testing their lifespan, and they find a sample mean of 5088.8 and a sample standard deviation of 214.93.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0379310417

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 8227 hours. To test the new design, the company samples 35 of the new lightbulbs, testing their lifespan, and they find a sample mean of 8330.8 and a sample standard deviation of 393.3.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0689452814

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 7 points. To test this, they randomly sample 86 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 7.4 and a sample standard deviation of 2.06.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0392853426

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 21.02 hours. They randomly sample 52 of the new model phones, testing the battery life, and find a sample mean of 21.1 and a sample standard deviation of 3.3.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0080472187

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 39.46 hours. They randomly sample 53 of the new model phones, testing the battery life, and find a sample mean of 40.6 and a sample standard deviation of 3.52.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0061085175

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 22 points. A clinical trial was conducted with 100 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 22.9 and a sample standard deviation of 3.84.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0115228150

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 2 points. To test this, they randomly sample 66 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 1.9 and a sample standard deviation of 4.19.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0935699725

The average lifespan in a particular country is 76.9 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 35 individuals in this region, recording their lifespans. They find a sample mean of 77 and a sample standard deviation of 4.68.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0017353557

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 20 points. A clinical trial was conducted with 36 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 21.8 and a sample standard deviation of 6.69.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0539351101

The average lifespan in a particular country is 70.55 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 58 individuals in this region, recording their lifespans. They find a sample mean of 69.7 and a sample standard deviation of 3.84.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0478143846

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 8 points. To test this, they randomly sample 49 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 6.5 and a sample standard deviation of 4.96.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0288855242

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 19 points. A clinical trial was conducted with 77 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 21.2 and a sample standard deviation of 5.5.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0557666376

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 2 points. To test this, they randomly sample 78 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 3 and a sample standard deviation of 4.33.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0234900503

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 8 points. To test this, they randomly sample 56 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 9 and a sample standard deviation of 3.89.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0462000423

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 24 points. A clinical trial was conducted with 89 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 25.7 and a sample standard deviation of 7.99.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0757179350

The average lifespan in a particular country is 77.8 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 51 individuals in this region, recording their lifespans. They find a sample mean of 77.4 and a sample standard deviation of 3.63.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0084228061

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 8427 hours. To test the new design, the company samples 93 of the new lightbulbs, testing their lifespan, and they find a sample mean of 8497.7 and a sample standard deviation of 315.08.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0379468683

The average lifespan in a particular country is 77.96 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 89 individuals in this region, recording their lifespans. They find a sample mean of 79 and a sample standard deviation of 3.57.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0428064987

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 2858 hours. To test the new design, the company samples 39 of the new lightbulbs, testing their lifespan, and they find a sample mean of 2832.9 and a sample standard deviation of 99.7.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0166270585

The average lifespan in a particular country is 65.17 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 96 individuals in this region, recording their lifespans. They find a sample mean of 65.7 and a sample standard deviation of 3.29.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0919131269

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 18 points. A clinical trial was conducted with 58 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 18.8 and a sample standard deviation of 3.45.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0948425839

The average lifespan in a particular country is 69.81 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 62 individuals in this region, recording their lifespans. They find a sample mean of 70.1 and a sample standard deviation of 3.82.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0349171942

The average lifespan in a particular country is 77.6 years. An anthropologist is studying a particular regional group of individuals from this country, who the anthropologist suspects live longer on average than other citizens of the country. To test this, the anthropologist randomly samples records from 43 individuals in this region, recording their lifespans. They find a sample mean of 78.5 and a sample standard deviation of 4.38.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0723332805

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 11 points. A clinical trial was conducted with 53 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 11.4 and a sample standard deviation of 4.87.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0130911302

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 69 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 3.3 and a sample standard deviation of 2.72.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0595360978

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 10 points. To test this, they randomly sample 58 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 9.6 and a sample standard deviation of 4.36.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0246944075

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 5 points. To test this, they randomly sample 48 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 5.5 and a sample standard deviation of 2.06.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0639550931

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 4879 hours. To test the new design, the company samples 35 of the new lightbulbs, testing their lifespan, and they find a sample mean of 4944.8 and a sample standard deviation of 209.83.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0905053198

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 15 points. A clinical trial was conducted with 100 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 14.5 and a sample standard deviation of 6.43.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0231647816

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 11 points. A clinical trial was conducted with 37 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12.8 and a sample standard deviation of 7.05.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0576660610

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 3 points. To test this, they randomly sample 50 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.9 and a sample standard deviation of 4.94.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0136071057

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 27.19 hours. They randomly sample 91 of the new model phones, testing the battery life, and find a sample mean of 27.4 and a sample standard deviation of 1.54.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0819530559

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students. To test this, they randomly sample 71 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of -0.7 and a sample standard deviation of 3.17.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0251217690

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 26.65 hours. They randomly sample 72 of the new model phones, testing the battery life, and find a sample mean of 26.6 and a sample standard deviation of 1.21.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0005843541

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 4639 hours. To test the new design, the company samples 80 of the new lightbulbs, testing their lifespan, and they find a sample mean of 4645.3 and a sample standard deviation of 146.96.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0568051756

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 5 points. To test this, they randomly sample 58 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 5.3 and a sample standard deviation of 3.57.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0487879652

A pyschologist is investigating the impact of a new treatment for depression on their patients. They suspect that it will result in an improvement to the standardized depression scores of their patients of at least 6 points. To test this, they randomly sample 78 patients, and provide the new treatment to them. They record the improvement in depression scores for each individual. They find a sample mean of 6 and a sample standard deviation of 1.43.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0194264301

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 36.54 hours. They randomly sample 69 of the new model phones, testing the battery life, and find a sample mean of 36.9 and a sample standard deviation of 2.53.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0671700101

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 42.44 hours. They randomly sample 45 of the new model phones, testing the battery life, and find a sample mean of 43.9 and a sample standard deviation of 3.87.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0643176946

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 69 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 12.9 and a sample standard deviation of 6.32.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0152706066

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 6023 hours. To test the new design, the company samples 76 of the new lightbulbs, testing their lifespan, and they find a sample mean of 6016.8 and a sample standard deviation of 262.03.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0339892582

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 12 points. A clinical trial was conducted with 49 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 14.4 and a sample standard deviation of 8.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0390992526

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 25.04 hours. They randomly sample 91 of the new model phones, testing the battery life, and find a sample mean of 26.6 and a sample standard deviation of 4.13.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0634805758

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 15 points. A clinical trial was conducted with 80 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 15.3 and a sample standard deviation of 1.7.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0226103312

A teacher is investigating the impact of a new teaching method for teaching statistics to their students. They suspect that it will result in an improvement to the test scores of their students of at least 3 points. To test this, they randomly sample 36 students to be given the new teaching method. They record the change in test scores for each individual. They find a sample mean of 2.6 and a sample standard deviation of 2.46.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0088242677

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 6921 hours. To test the new design, the company samples 36 of the new lightbulbs, testing their lifespan, and they find a sample mean of 7036.8 and a sample standard deviation of 238.23.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0069488300

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 10129 hours. To test the new design, the company samples 62 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10104 and a sample standard deviation of 300.64.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0043724328

A lightbulb manufacturer comes up with a new design that they hope will lead to a longer-lasting lightbulb. Their existing design is rated for an average of 10602 hours. To test the new design, the company samples 65 of the new lightbulbs, testing their lifespan, and they find a sample mean of 10668.5 and a sample standard deviation of 344.56.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0767591133

A pharmaceutical company claims their new cholesterol-lowering medication reduces cholesterol levels by an average of at least 23 points. A clinical trial was conducted with 92 patients to test this claim. For each patient, the researchers measured their reduction in cholesterol level. The researchers found a sample mean of 23.1 and a sample standard deviation of 2.49.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.2\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0061641034

A phone manufacturer has designed a new model of phone. They wish to test whether their new phone has a battery life that exceeds that of their outgoing model. Their previous model has an average life of 38.12 hours. They randomly sample 71 of the new model phones, testing the battery life, and find a sample mean of 37.9 and a sample standard deviation of 2.64.

1. What is the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0539693562

Self Assessment 15.10

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.79 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1575 times, recording a six on 1260 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0470500595

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.05 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1083 parts, measuring their mass. They find that 11 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0398437481

An existing surgical intervention is successful with probability 0.29 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1062 patients, and observe that 319 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0965154451

In the general population, a particular disease has prevalence 0.2 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1151 individuals from this subpopulation, and find that 230 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0968802076

A pollster wants to determine whether the support for a particular issue in a region is less than 0.42 . They take a random sample of 149 individuals, observing that 60 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0938548238

In the general population, a particular disease has prevalence 0.03 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 457 individuals from this subpopulation, and find that 5 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0223487281

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.47 . They take a random sample of 99 individuals, observing that 50 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0177001661

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.4 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 169 times, recording a six on 68 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0340536977

In the general population, a particular disease has prevalence 0.05 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 235 individuals from this subpopulation, and find that 2 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0064702149

An existing surgical intervention is successful with probability 0.69 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1052 patients, and observe that 736 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0996583429

A correctly functioning machine at a particular factory is calibrated so that in at least 0.92 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1581 parts, measuring their mass. They find that 1423 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0545014579

An existing surgical intervention is successful with probability 0.55 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 134 patients, and observe that 80 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0264330440

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.35 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 702 times, seeing heads on 211 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0260585832

A correctly functioning machine at a particular factory is calibrated so that in 0.09 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 290 parts, measuring their mass. They find that 29 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0655775031

In the general population, a particular disease has prevalence 0.1 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 703 individuals from this subpopulation, and find that 70 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0427920438

In the general population, a particular disease has prevalence 0.19 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 979 individuals from this subpopulation, and find that 196 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0178086414

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.52 . They take a random sample of 440 individuals, observing that 220 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0780801848

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.49 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1867 times, seeing heads on 934 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0636642548

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.52 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1042 times, recording a six on 521 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0579346777

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.57 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 250 times, seeing heads on 150 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0012644967

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.02 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1275 times, recording a six on 13 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0015282119

A pollster wants to determine whether the support for a particular issue in a region is less than 0.45 . They take a random sample of 69 individuals, observing that 28 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0797895705

An existing surgical intervention is successful with probability 0.58 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1858 patients, and observe that 1115 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0724474954

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.54 . They take a random sample of 1156 individuals, observing that 694 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0233031581

A correctly functioning machine at a particular factory is calibrated so that in 0.02 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1413 parts, measuring their mass. They find that 14 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0137236740

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.48 . They take a random sample of 1999 individuals, observing that 1000 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0518838277

In the general population, a particular disease has prevalence 0.02 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 1741 individuals from this subpopulation, and find that 17 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0284464338

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.43 . They take a random sample of 872 individuals, observing that 349 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0693775764

An existing surgical intervention is successful with probability 0.38 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 1810 patients, and observe that 724 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0691422423

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.56 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 575 times, seeing heads on 345 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0653133440

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.61 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 475 times, seeing heads on 285 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0792866682

In the general population, a particular disease has prevalence 0.2 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 1480 individuals from this subpopulation, and find that 296 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0663562008

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.45 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1849 times, recording a six on 740 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0343279170

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.81 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 159 times, recording a six on 127 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0157602059

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.12 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 676 times, recording a six on 68 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.11\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0638047880

An existing surgical intervention is successful with probability 0.68 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 2000 patients, and observe that 1400 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0214393442

In the general population, a particular disease has prevalence 0.14 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 1426 individuals from this subpopulation, and find that 143 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0535512887

An existing surgical intervention is successful with probability 0.66 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1159 patients, and observe that 695 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0594323754

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.08 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 241 times, recording a six on 24 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0457922395

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.46 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 241 times, seeing heads on 96 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0456567739

An existing surgical intervention is successful with probability 0.66 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 720 patients, and observe that 432 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0951014591

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.31 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 191 times, seeing heads on 57 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0328340262

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.56 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 176 times, seeing heads on 106 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0999224773

An existing surgical intervention is successful with probability 0.28 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 1788 patients, and observe that 536 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0176482810

An existing surgical intervention is successful with probability 0.45 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1924 patients, and observe that 962 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0533377372

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.46 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1357 times, seeing heads on 543 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0889717408

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.47 . They take a random sample of 736 individuals, observing that 368 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0806403053

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.4 . They take a random sample of 1873 individuals, observing that 749 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0548752339

A correctly functioning machine at a particular factory is calibrated so that in at least 0.95 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1306 parts, measuring their mass. They find that 1293 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0177314128

A correctly functioning machine at a particular factory is calibrated so that in at least 0.94 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1216 parts, measuring their mass. They find that 1094 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0110435723

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.02 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 635 times, recording a six on 6 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0343630589

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.6 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 35 times, seeing heads on 18 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0959580553

An existing surgical intervention is successful with probability 0.49 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1455 patients, and observe that 728 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0944840886

In the general population, a particular disease has prevalence 0.2 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1878 individuals from this subpopulation, and find that 376 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.05\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0219761200

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.67 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1532 times, recording a six on 1072 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0389152800

An existing surgical intervention is successful with probability 0.43 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 623 patients, and observe that 249 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0518420849

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.57 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 221 times, seeing heads on 133 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0342544737

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.55 . They take a random sample of 827 individuals, observing that 496 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.08\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0187374156

A pollster wants to determine whether the support for a particular issue in a region is less than 0.52 . They take a random sample of 1096 individuals, observing that 548 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0213403197

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.48 . They take a random sample of 1083 individuals, observing that 542 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0946790630

An existing surgical intervention is successful with probability 0.76 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 1446 patients, and observe that 1157 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0724034560

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.65 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 760 times, recording a six on 532 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0989498536

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.57 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1070 times, seeing heads on 642 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0754227456

A correctly functioning machine at a particular factory is calibrated so that in at least 0.98 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1246 parts, measuring their mass. They find that 1234 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.12\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0662881315

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.03 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1160 times, recording a six on 12 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0835861161

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.46 . They take a random sample of 481 individuals, observing that 240 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0267894888

An existing surgical intervention is successful with probability 0.7 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 426 patients, and observe that 298 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0320340051

An existing surgical intervention is successful with probability 0.48 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 907 patients, and observe that 454 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0626942916

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.52 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1880 times, recording a six on 940 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.03\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0215820876

In the general population, a particular disease has prevalence 0.11 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 1101 individuals from this subpopulation, and find that 110 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0951672865

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.09 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1577 parts, measuring their mass. They find that 158 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0199021629

A correctly functioning machine at a particular factory is calibrated so that in at least 0.92 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 772 parts, measuring their mass. They find that 695 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0221043274

In the general population, a particular disease has prevalence 0.11 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 957 individuals from this subpopulation, and find that 96 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0293508305

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.06 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1993 parts, measuring their mass. They find that 199 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.07\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0487171700

An existing surgical intervention is successful with probability 0.41 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 163 patients, and observe that 65 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0190817611

An existing surgical intervention is successful with probability 0.62 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 537 patients, and observe that 322 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0502459519

An existing surgical intervention is successful with probability 0.62 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 1056 patients, and observe that 634 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0239275350

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.12 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1240 times, recording a six on 124 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0859448746

In the general population, a particular disease has prevalence 0.16 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1699 individuals from this subpopulation, and find that 170 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.02\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0505258519

An existing surgical intervention is successful with probability 0.62 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 1704 patients, and observe that 1022 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0136770815

In the general population, a particular disease has prevalence 0.08 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 1707 individuals from this subpopulation, and find that 171 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.06\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0426594587

A correctly functioning machine at a particular factory is calibrated so that in at least 0.96 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1287 parts, measuring their mass. They find that 1274 parts satisfy of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.19\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0763896442

A correctly functioning machine at a particular factory is calibrated so that in 0.08 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1259 parts, measuring their mass. They find that 126 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0068257665

A correctly functioning machine at a particular factory is calibrated so that in 0.08 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 980 parts, measuring their mass. They find that 98 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.14\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0824101247

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.65 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 422 times, seeing heads on 295 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0970778030

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.36 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 729 times, recording a six on 292 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0354251558

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.56 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 327 times, recording a six on 196 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0761298958

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.09 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 671 parts, measuring their mass. They find that 67 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.17\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0822852744

An existing surgical intervention is successful with probability 0.77 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 233 patients, and observe that 186 of the surgeries are successful.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.16\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0725733570

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.08 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1468 parts, measuring their mass. They find that 147 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0781151881

A correctly functioning machine at a particular factory is calibrated so that in 0.03 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 636 parts, measuring their mass. They find that 6 parts are outside of mass tolerances.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.01\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0760009019

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.57 . They take a random sample of 61 individuals, observing that 30 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.09\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0434698759

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.55 . They take a random sample of 1974 individuals, observing that 1184 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0455712625

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.67 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 90 times, recording a six on 63 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0704579198

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.52 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 880 times, seeing heads on 440 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.04\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0892139522

A pollster wants to determine whether the support for a particular issue in a region is less than 0.47 . They take a random sample of 1829 individuals, observing that 914 individuals support the issue.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.13\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0099311156

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.44 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 350 times, recording a six on 175 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0818419333

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.39 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1903 times, recording a six on 761 rolls.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.18\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0762700405

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.49 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 54 times, seeing heads on 27 flips.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.1\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0960062355

In the general population, a particular disease has prevalence 0.02 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 771 individuals from this subpopulation, and find that 8 individuals have the disease.

1. What is the magnitude of the critical value for the associated hypothesis test, at \(\alpha = 0.15\)?
2. What is the relevant value of the test statistic for testing the null hypothesis?
3. What is the conclusion from the hypothesis test?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0746679035

Self Assessment 15.11

In the general population, a particular disease has prevalence 0.19 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 462 individuals from this subpopulation, and find that 92 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0767977368

In the general population, a particular disease has prevalence 0.14 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 647 individuals from this subpopulation, and find that 65 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0019068947

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.81 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 911 times, recording a six on 729 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0969192978

An existing surgical intervention is successful with probability 0.34 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1101 patients, and observe that 330 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0805288220

A pollster wants to determine whether the support for a particular issue in a region is less than 0.41 . They take a random sample of 624 individuals, observing that 250 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0495443419

An existing surgical intervention is successful with probability 0.65 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 1172 patients, and observe that 820 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0173636447

In the general population, a particular disease has prevalence 0.03 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 573 individuals from this subpopulation, and find that 6 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0344872200

In the general population, a particular disease has prevalence 0.02 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 765 individuals from this subpopulation, and find that 8 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0890461245

In the general population, a particular disease has prevalence 0.1 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 530 individuals from this subpopulation, and find that 53 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0006860580

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.67 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 432 times, recording a six on 302 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0382093352

In the general population, a particular disease has prevalence 0.16 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 524 individuals from this subpopulation, and find that 105 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0606207761

In the general population, a particular disease has prevalence 0.11 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 1471 individuals from this subpopulation, and find that 147 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0043418481

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.04 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 784 parts, measuring their mass. They find that 8 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0306546178

An existing surgical intervention is successful with probability 0.39 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 847 patients, and observe that 339 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0129317347

An existing surgical intervention is successful with probability 0.67 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1269 patients, and observe that 888 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0173306236

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.32 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1820 times, seeing heads on 546 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0216532049

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.46 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1153 times, recording a six on 576 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0277140302

In the general population, a particular disease has prevalence 0.19 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 81 individuals from this subpopulation, and find that 16 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0822488643

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.03 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 507 parts, measuring their mass. They find that 5 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0724546014

An existing surgical intervention is successful with probability 0.21 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 850 patients, and observe that 170 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0693918970

An existing surgical intervention is successful with probability 0.46 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 61 patients, and observe that 30 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0357825150

A pollster wants to determine whether the support for a particular issue in a region is less than 0.4 . They take a random sample of 972 individuals, observing that 389 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0381429971

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.05 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1690 parts, measuring their mass. They find that 17 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0970673024

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.02 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1169 times, recording a six on 12 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0206291753

An existing surgical intervention is successful with probability 0.32 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 483 patients, and observe that 145 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0817540147

A correctly functioning machine at a particular factory is calibrated so that in 0.04 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 515 parts, measuring their mass. They find that 5 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0649880812

In the general population, a particular disease has prevalence 0.17 . Researchersare interested in whether the prevalence in a particular subpopulation with heightened risk factors is actually greater than the overall average. They sample 751 individuals from this subpopulation, and find that 150 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0879047520

A correctly functioning machine at a particular factory is calibrated so that in at least 0.9 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1396 parts, measuring their mass. They find that 1256 parts satisfy of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0801434031

An existing surgical intervention is successful with probability 0.36 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1082 patients, and observe that 433 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0699536132

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.56 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 828 times, recording a six on 414 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0580367026

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.07 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1397 parts, measuring their mass. They find that 140 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0623500625

In the general population, a particular disease has prevalence 0.05 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1590 individuals from this subpopulation, and find that 16 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0288576480

An existing surgical intervention is successful with probability 0.66 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 881 patients, and observe that 529 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0385893125

An existing surgical intervention is successful with probability 0.36 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 127 patients, and observe that 51 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0893863124

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.57 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1128 times, seeing heads on 677 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0810825106

A pollster wants to determine whether the support for a particular issue in a region is less than 0.6 . They take a random sample of 925 individuals, observing that 555 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0233500625

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.45 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 349 times, seeing heads on 174 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0332648476

An existing surgical intervention is successful with probability 0.68 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 128 patients, and observe that 90 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0754449597

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.02 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1296 parts, measuring their mass. They find that 13 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0427704146

An existing surgical intervention is successful with probability 0.58 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 453 patients, and observe that 226 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0984494824

In the general population, a particular disease has prevalence 0.1 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 281 individuals from this subpopulation, and find that 28 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0285975607

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.53 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1332 times, seeing heads on 799 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0827825380

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.58 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 139 times, recording a six on 83 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0246505472

In the general population, a particular disease has prevalence 0.17 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 761 individuals from this subpopulation, and find that 152 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0112585420

In the general population, a particular disease has prevalence 0.17 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 538 individuals from this subpopulation, and find that 108 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0607226869

In the general population, a particular disease has prevalence 0.04 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 298 individuals from this subpopulation, and find that 3 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0547692597

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.58 . They take a random sample of 373 individuals, observing that 224 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0037996018

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.46 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1573 times, seeing heads on 786 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0687582298

A correctly functioning machine at a particular factory is calibrated so that in at least 0.91 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1063 parts, measuring their mass. They find that 957 parts satisfy of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0161525534

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.55 . They take a random sample of 547 individuals, observing that 328 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0535423919

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.35 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1878 times, seeing heads on 563 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.06\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0746016222

In the general population, a particular disease has prevalence 0.18 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1004 individuals from this subpopulation, and find that 201 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0203304534

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.09 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1749 parts, measuring their mass. They find that 175 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0153708708

An existing surgical intervention is successful with probability 0.44 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1976 patients, and observe that 790 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0962013306

In the general population, a particular disease has prevalence 0.11 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 370 individuals from this subpopulation, and find that 37 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0308864687

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.07 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1661 parts, measuring their mass. They find that 166 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.12\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0151756148

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.58 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 677 times, seeing heads on 406 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0663063121

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.57 . They take a random sample of 701 individuals, observing that 421 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0512528819

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.55 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 172 times, seeing heads on 86 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0681844642

In the general population, a particular disease has prevalence 0.04 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 1482 individuals from this subpopulation, and find that 15 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.13\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0836838930

In the general population, a particular disease has prevalence 0.15 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 796 individuals from this subpopulation, and find that 80 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0860761119

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.48 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 801 times, seeing heads on 400 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0246189118

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.72 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 735 times, recording a six on 514 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0891162619

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.36 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 216 times, seeing heads on 65 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0979103454

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.67 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 946 times, seeing heads on 662 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0731590160

An existing surgical intervention is successful with probability 0.75 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 597 patients, and observe that 418 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202623119

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of 0.46 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1409 times, seeing heads on 564 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0780273952

A pollster wants to determine whether the support for a particular issue in a region is less than 0.49 . They take a random sample of 1614 individuals, observing that 807 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0817709247

An existing surgical intervention is successful with probability 0.34 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 415 patients, and observe that 166 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.2\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0102898879

An existing surgical intervention is successful with probability 0.53 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 631 patients, and observe that 316 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0151355964

In the general population, a particular disease has prevalence 0.03 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 827 individuals from this subpopulation, and find that 8 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0631722798

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.03 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 739 times, recording a six on 7 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0855856021

An existing surgical intervention is successful with probability 0.38 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement and substantially cheaper. They worry, however, that it may be worse at treating the disease compared to the existing procedure. To test this concern, they have the new technique applied for 987 patients, and observe that 395 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0084013312

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.45 . They take a random sample of 674 individuals, observing that 270 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0348621692

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.38 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1584 times, recording a six on 634 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0780426465

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.45 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 167 times, recording a six on 84 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.15\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0016872929

A correctly functioning machine at a particular factory is calibrated so that in 0.07 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1587 parts, measuring their mass. They find that 159 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0267348992

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.46 . They take a random sample of 1987 individuals, observing that 994 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0522420635

A pollster wants to determine whether the support for a particular issue in a region is less than 0.5 . They take a random sample of 1228 individuals, observing that 614 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.02\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0792132795

A correctly functioning machine at a particular factory is calibrated so that in 0.08 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 142 parts, measuring their mass. They find that 14 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0290426267

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of no more than 0.44 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1225 times, seeing heads on 490 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0300502405

An existing surgical intervention is successful with probability 0.59 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 595 patients, and observe that 357 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.08\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0267424204

An existing surgical intervention is successful with probability 0.55 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 1677 patients, and observe that 1006 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0669602878

A correctly functioning machine at a particular factory is calibrated so that in 0.09 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1261 parts, measuring their mass. They find that 126 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.17\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0960787381

A pollster wants to determine whether the support for a particular issue in a region is less than 0.55 . They take a random sample of 1927 individuals, observing that 964 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0532907769

An existing surgical intervention is successful with probability 0.59 at treating an underlying condition. A research surgeon has developed a new technique, which is easier to implement, and they want to understand its effectiveness. They have the new technique applied for 805 patients, and observe that 483 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.14\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0330991941

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.44 . They take a random sample of 1247 individuals, observing that 624 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0864260532

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.48 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 471 times, recording a six on 236 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.03\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0213649415

A woodworker is attempting to construct a biased six-sided die that shows a six with probability no more than 0.02 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 967 times, recording a six on 10 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.01\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0783679365

A pollster wants to determine whether the support for a particular issue in a region exceeds 0.6 . They take a random sample of 385 individuals, observing that 231 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0619377367

A correctly functioning machine at a particular factory is calibrated so that in at least 0.96 proportion of cases, the mass of the produced product is within the bounds of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 1162 parts, measuring their mass. They find that 1150 parts satisfy of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0722180043

A pollster wants to determine whether the support for a particular issue in a region is less than 0.49 . They take a random sample of 1033 individuals, observing that 516 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.16\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0768650476

In the general population, a particular disease has prevalence 0.04 . Researchersare interested in whether the prevalence in a particular subpopulation is equivalent. They sample 540 individuals from this subpopulation, and find that 5 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.11\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0610404007

A pollster wants to determine whether the support for a particular issue in a region differs meaningfully from 0.41 . They take a random sample of 1566 individuals, observing that 626 individuals support the issue.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.07\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0423043519

In the general population, a particular disease has prevalence 0.17 . Researchersare interested in whether the prevalence in a particular subpopulation who appear to have certain protective lifestyle factors is actually less than the overall average. They sample 552 individuals from this subpopulation, and find that 110 individuals have the disease.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.19\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0166938010

A woodworker is attempting to construct a biased six-sided die that shows a six with probability at least 0.41 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 1713 times, recording a six on 685 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.18\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0514085186

A correctly functioning machine at a particular factory is calibrated so that in no more than 0.07 proportion of cases, the mass of the produced product is outside of tolerance. A group of engineers need to test the calibration on the machine, so they randomly sample 262 parts, measuring their mass. They find that 26 parts are outside of mass tolerances.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.1\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0646221882

An existing surgical intervention is successful with probability 0.8 at treating an underlying condition. A research surgeon has developed a new technique, that they suspect should be more effective at treating the disease. They have the new technique applied for 1235 patients, and observe that 988 of the surgeries are successful.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.04\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0373806168

An amateur magician has a collection of biased coins that turn up heads with certain probabilities. The magician purchases a new coin that claims it has a probability of at least 0.69 of showing heads. Past experience suggests that these coins are not always correctly calibrated, and as such, the magician decides to test the claim. They flip the coin 1362 times, seeing heads on 953 flips.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.05\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0723341672

A woodworker is attempting to construct a biased six-sided die that shows a six with probability 0.8 . In order to test to see if their construction is acceptable, they take a prototype, and roll the die 962 times, recording a six on 770 rolls.

1. What is the relevant value of the test statistic for testing the null hypothesis?
2. What is the \(p\)-value for the associated hypothesis test?
3. What is the conclusion from the hypothesis test, at \(\alpha = 0.09\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0764071445

Self Assessment 15.12

Which of the following scenarios describes a type I error?

(Question ID: 0836515121)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.

Which of the following scenarios describes a type I error?

(Question ID: 0678259292)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type II error?

(Question ID: 0764437851)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type I error?

(Question ID: 0202243601)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A jury finds a defendant guilty, but the defendant is actually innocent.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type II error?

(Question ID: 0702012494)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.

Which of the following scenarios describes a type I error?

(Question ID: 0727982787)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type I error?

(Question ID: 0638123525)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A jury finds a defendant guilty, but the defendant is actually innocent.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type II error?

(Question ID: 0316851943)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type II error?

(Question ID: 0608943603)

A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type I error?

(Question ID: 0746633899)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type II error?

(Question ID: 0388850299)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.

Which of the following scenarios describes a type I error?

(Question ID: 0485514808)

A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type II error?

(Question ID: 0275419433)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A jury finds a defendant guilty, but the defendant is actually innocent.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.

Which of the following scenarios describes a type I error?

(Question ID: 0208673561)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.

Which of the following scenarios describes a type II error?

(Question ID: 0892210406)

A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.

Which of the following scenarios describes a type I error?

(Question ID: 0573114302)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type I error?

(Question ID: 0733894566)

A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type II error?

(Question ID: 0350657301)

A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.

Which of the following scenarios describes a type II error?

(Question ID: 0591818005)

A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A jury finds a defendant guilty, but the defendant is actually innocent.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.

Which of the following scenarios describes a type II error?

(Question ID: 0313297020)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A jury finds a defendant guilty, but the defendant is actually innocent.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.

Which of the following scenarios describes a type I error?

(Question ID: 0968639913)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.

Which of the following scenarios describes a type II error?

(Question ID: 0854678019)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A jury finds a defendant guilty, but the defendant is actually innocent.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.

Which of the following scenarios describes a type I error?

(Question ID: 0932975554)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.

Which of the following scenarios describes a type II error?

(Question ID: 0764313778)

A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type I error?

(Question ID: 0891552548)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type II error?

(Question ID: 0377651560)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A jury finds a defendant guilty, but the defendant is actually innocent.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.

Which of the following scenarios describes a type I error?

(Question ID: 0556179085)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type II error?

(Question ID: 0534165549)

A jury finds a defendant guilty, but the defendant is actually innocent.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type I error?

(Question ID: 0321214413)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type II error?

(Question ID: 0251614027)

A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.

Which of the following scenarios describes a type I error?

(Question ID: 0739618896)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type II error?

(Question ID: 0865600858)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type II error?

(Question ID: 0730752626)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type I error?

(Question ID: 0253158344)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type I error?

(Question ID: 0303378239)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.

Which of the following scenarios describes a type II error?

(Question ID: 0640371415)

A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A jury finds a defendant guilty, but the defendant is actually innocent.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type II error?

(Question ID: 0607539160)

A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.

Which of the following scenarios describes a type I error?

(Question ID: 0391327925)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type II error?

(Question ID: 0622711943)

A jury finds a defendant guilty, but the defendant is actually innocent.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type II error?

(Question ID: 0259243696)

A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.

Which of the following scenarios describes a type II error?

(Question ID: 0819415158)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type II error?

(Question ID: 0213198834)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.

Which of the following scenarios describes a type II error?

(Question ID: 0220730739)

A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A jury finds a defendant guilty, but the defendant is actually innocent.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.

Which of the following scenarios describes a type I error?

(Question ID: 0590542284)

A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.

Which of the following scenarios describes a type I error?

(Question ID: 0848990316)

A jury finds a defendant guilty, but the defendant is actually innocent.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Which of the following scenarios describes a type I error?

(Question ID: 0897962718)

A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.

Which of the following scenarios describes a type I error?

(Question ID: 0422416909)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.

Which of the following scenarios describes a type I error?

(Question ID: 0200989611)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A jury finds a defendant guilty, but the defendant is actually innocent.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.

Which of the following scenarios describes a type II error?

(Question ID: 0248449745)

A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type I error?

(Question ID: 0533876699)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type II error?

(Question ID: 0597465573)

An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A jury finds a defendant guilty, but the defendant is actually innocent.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type I error?

(Question ID: 0553115769)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.

Which of the following scenarios describes a type I error?

(Question ID: 0743914419)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.

Which of the following scenarios describes a type II error?

(Question ID: 0882002748)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A jury finds a defendant guilty, but the defendant is actually innocent.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type II error?

(Question ID: 0368343108)

A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A jury finds a defendant guilty, but the defendant is actually innocent.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type I error?

(Question ID: 0365784061)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.

Which of the following scenarios describes a type II error?

(Question ID: 0453728857)

A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.

Which of the following scenarios describes a type I error?

(Question ID: 0464544765)

A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.

Which of the following scenarios describes a type II error?

(Question ID: 0682873412)

A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A jury finds a defendant guilty, but the defendant is actually innocent.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.

Which of the following scenarios describes a type I error?

(Question ID: 0650952590)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.

Which of the following scenarios describes a type II error?

(Question ID: 0519722780)

A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.

Which of the following scenarios describes a type II error?

(Question ID: 0144069449)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.

Which of the following scenarios describes a type I error?

(Question ID: 0067494777)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.

Which of the following scenarios describes a type I error?

(Question ID: 0148188274)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.

Which of the following scenarios describes a type II error?

(Question ID: 0245207848)

A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type I error?

(Question ID: 0286704699)

A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A jury finds a defendant guilty, but the defendant is actually innocent.

Which of the following scenarios describes a type II error?

(Question ID: 0280967107)

A fire alarm goes off in a building, and everyone evacuates, even though there is no actual fire.A study fails to find a statistically significant difference in effectiveness between a new drug and a placebo, even though the new drug is actually more effective.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.

Which of the following scenarios describes a type I error?

(Question ID: 0065867762)

A quality control inspector at a light bulb factory rejects a batch of light bulbs because the sample mean lifespan is significantly lower than the claimed lifespan. However, the batch actually meets the claimed lifespan.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A scientist concludes that there is no link between a certain gene and a disease, when in reality, the gene does play a role in the disease.A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.

Which of the following scenarios describes a type II error?

(Question ID: 0151351400)

A medical researcher fails to reject the null hypothesis that a new drug has no effect, even though the drug actually does have a statistically significant positive effect.A doctor diagnoses a patient with a rare disease based on a positive test result. However, the patient does not actually have the disease.A store owner believes a new advertising campaign has increased sales, but in reality, sales have not changed. The owner proceeds with the expensive campaign.A teacher believes a new teaching method improves test scores and implements it. However, the new method has no actual impact on test scores.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.

Which of the following scenarios describes a type I error?

(Question ID: 0145908981)

A study concludes that a pollutant has no significant effect on a local ecosystem, even though the pollutant is causing harm.An investor decides that a stock is actually fairly valued, and does not invest, even though the stock is actually undervalued and likely to increase in price.A company decides to launch a new product based on a market survey that showed significant interest. However, the survey results were flawed, and there is actually little real interest in the product.A farmer decides not to use a new fertilizer because a hypothesis test showed no significant increase in crop yield. However, the fertilizer would have actually increased the yield.A public health official concludes that a new disease outbreak is not serious, even though it is a significant threat.

Self Assessment 15.13

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 135 mmHg. They want to be able to detect a true average blood pressure change of 1.94 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.21 mmHg. They will test using \(\alpha = 0.01\).

1. In a sample of size \(42\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0229320908

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 1.38 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.48 mmHg. They will test using \(\alpha = 0.05\).

1. In a sample of size \(37\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.88\)?

Question ID: 0886901498

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 1.28 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.46 mmHg. They will test using \(\alpha = 0.11\).

1. In a sample of size \(67\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0994646909

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 144 mmHg. They want to be able to detect a true average blood pressure change of 1.05 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.83 mmHg. They will test using \(\alpha = 0.12\).

1. In a sample of size \(70\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.88\)?

Question ID: 0688510478

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 1.45 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.49 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(97\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0593245517

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 146 mmHg. They want to be able to detect a true average blood pressure change of 1.17 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.28 mmHg. They will test using \(\alpha = 0.19\).

1. In a sample of size \(93\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0473158422

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 1.64 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.39 mmHg. They will test using \(\alpha = 0.07\).

1. In a sample of size \(68\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.89\)?

Question ID: 0176897642

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 139 mmHg. They want to be able to detect a true average blood pressure change of 1.64 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.29 mmHg. They will test using \(\alpha = 0.06\).

1. In a sample of size \(98\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0459941297

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 148 mmHg. They want to be able to detect a true average blood pressure change of 0.87 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.05 mmHg. They will test using \(\alpha = 0.2\).

1. In a sample of size \(83\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0506696134

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 148 mmHg. They want to be able to detect a true average blood pressure change of 1.8 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.78 mmHg. They will test using \(\alpha = 0.15\).

1. In a sample of size \(58\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0063723280

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 139 mmHg. They want to be able to detect a true average blood pressure change of 4.06 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.22 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(75\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0803634989

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 147 mmHg. They want to be able to detect a true average blood pressure change of 2.82 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.31 mmHg. They will test using \(\alpha = 0.09\).

1. In a sample of size \(93\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0617225116

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 2.2 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.18 mmHg. They will test using \(\alpha = 0.15\).

1. In a sample of size \(50\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0757077521

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 144 mmHg. They want to be able to detect a true average blood pressure change of 1.07 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.12 mmHg. They will test using \(\alpha = 0.01\).

1. In a sample of size \(77\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.86\)?

Question ID: 0462699496

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 1.99 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.98 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(61\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0309731167

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 0.79 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.41 mmHg. They will test using \(\alpha = 0.04\).

1. In a sample of size \(88\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.81\)?

Question ID: 0221582486

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 2.38 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.55 mmHg. They will test using \(\alpha = 0.07\).

1. In a sample of size \(80\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0716418910

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 139 mmHg. They want to be able to detect a true average blood pressure change of 1.16 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.84 mmHg. They will test using \(\alpha = 0.18\).

1. In a sample of size \(84\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.89\)?

Question ID: 0467477713

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 1.64 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.17 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(93\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0141406766

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 134 mmHg. They want to be able to detect a true average blood pressure change of 1.67 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.3 mmHg. They will test using \(\alpha = 0.05\).

1. In a sample of size \(84\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0998147924

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 1.61 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.87 mmHg. They will test using \(\alpha = 0.01\).

1. In a sample of size \(57\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.88\)?

Question ID: 0031586333

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 0.54 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.48 mmHg. They will test using \(\alpha = 0.04\).

1. In a sample of size \(72\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.84\)?

Question ID: 0250182279

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 1.34 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.15 mmHg. They will test using \(\alpha = 0.01\).

1. In a sample of size \(60\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0872488688

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 135 mmHg. They want to be able to detect a true average blood pressure change of 3.38 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.82 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(60\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0855295622

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 0.99 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.25 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(37\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0343840912

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 146 mmHg. They want to be able to detect a true average blood pressure change of 1.37 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.12 mmHg. They will test using \(\alpha = 0.13\).

1. In a sample of size \(78\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.86\)?

Question ID: 0098705400

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 147 mmHg. They want to be able to detect a true average blood pressure change of 1.37 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.28 mmHg. They will test using \(\alpha = 0.12\).

1. In a sample of size \(43\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0353255609

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 148 mmHg. They want to be able to detect a true average blood pressure change of 1.48 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.83 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(78\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.89\)?

Question ID: 0005819803

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 2.6 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.22 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(56\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0234799107

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 132 mmHg. They want to be able to detect a true average blood pressure change of 1.28 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.63 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(75\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0719226873

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 2.33 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.13 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(59\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0618676651

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 2.04 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.96 mmHg. They will test using \(\alpha = 0.04\).

1. In a sample of size \(97\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0265801730

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 142 mmHg. They want to be able to detect a true average blood pressure change of 1.67 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.28 mmHg. They will test using \(\alpha = 0.14\).

1. In a sample of size \(91\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.86\)?

Question ID: 0652636111

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 0.86 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.99 mmHg. They will test using \(\alpha = 0.12\).

1. In a sample of size \(72\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0505252848

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 1.07 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.43 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(37\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0375092226

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 145 mmHg. They want to be able to detect a true average blood pressure change of 1.55 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.5 mmHg. They will test using \(\alpha = 0.07\).

1. In a sample of size \(78\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0628493850

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 0.98 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.19 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(46\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0635795574

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 1.17 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.05 mmHg. They will test using \(\alpha = 0.09\).

1. In a sample of size \(35\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0302986953

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 0.66 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.61 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(71\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0841346777

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 1.33 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.35 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(39\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0422796476

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 0.5 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.05 mmHg. They will test using \(\alpha = 0.12\).

1. In a sample of size \(87\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0116382644

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 137 mmHg. They want to be able to detect a true average blood pressure change of 0.49 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.25 mmHg. They will test using \(\alpha = 0.11\).

1. In a sample of size \(35\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.81\)?

Question ID: 0162790183

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 1.45 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.68 mmHg. They will test using \(\alpha = 0.14\).

1. In a sample of size \(86\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0591047097

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 137 mmHg. They want to be able to detect a true average blood pressure change of 0.56 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.89 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(98\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0111601480

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 0.45 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.78 mmHg. They will test using \(\alpha = 0.15\).

1. In a sample of size \(74\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.81\)?

Question ID: 0510302048

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 1.16 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.67 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(58\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.84\)?

Question ID: 0401257312

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 1.35 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.52 mmHg. They will test using \(\alpha = 0.11\).

1. In a sample of size \(83\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0868075932

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 142 mmHg. They want to be able to detect a true average blood pressure change of 0.99 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.69 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(66\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0753565708

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 0.71 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.28 mmHg. They will test using \(\alpha = 0.04\).

1. In a sample of size \(86\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0464187907

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 1.1 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.68 mmHg. They will test using \(\alpha = 0.09\).

1. In a sample of size \(87\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0521968718

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 144 mmHg. They want to be able to detect a true average blood pressure change of 1.13 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.82 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(100\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.8\)?

Question ID: 0428635621

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 1.29 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.31 mmHg. They will test using \(\alpha = 0.07\).

1. In a sample of size \(45\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0978943620

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 135 mmHg. They want to be able to detect a true average blood pressure change of 0.93 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.36 mmHg. They will test using \(\alpha = 0.18\).

1. In a sample of size \(37\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0417445313

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 146 mmHg. They want to be able to detect a true average blood pressure change of 1.16 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.97 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(77\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0863396205

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 2.95 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.33 mmHg. They will test using \(\alpha = 0.13\).

1. In a sample of size \(49\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0196889179

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 1.53 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.33 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(56\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0104380140

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 1.38 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.41 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(44\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.88\)?

Question ID: 0847800420

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 148 mmHg. They want to be able to detect a true average blood pressure change of 0.58 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.34 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(56\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0359684515

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 0.79 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.78 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(93\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0148377545

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 134 mmHg. They want to be able to detect a true average blood pressure change of 1.85 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.75 mmHg. They will test using \(\alpha = 0.05\).

1. In a sample of size \(55\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.88\)?

Question ID: 0697404374

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 135 mmHg. They want to be able to detect a true average blood pressure change of 0.71 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.76 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(96\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0558438091

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 146 mmHg. They want to be able to detect a true average blood pressure change of 1.67 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.3 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(67\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0006170176

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 137 mmHg. They want to be able to detect a true average blood pressure change of 0.49 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.18 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(43\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0233220172

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 0.55 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.26 mmHg. They will test using \(\alpha = 0.15\).

1. In a sample of size \(40\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0891319236

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 0.79 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.33 mmHg. They will test using \(\alpha = 0.18\).

1. In a sample of size \(96\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0138722817

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 140 mmHg. They want to be able to detect a true average blood pressure change of 2.22 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.56 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(82\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0334604159

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 0.83 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.95 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(37\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0775994507

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 1.53 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.91 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(80\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0801550781

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 142 mmHg. They want to be able to detect a true average blood pressure change of 0.86 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.14 mmHg. They will test using \(\alpha = 0.19\).

1. In a sample of size \(61\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0313947301

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 137 mmHg. They want to be able to detect a true average blood pressure change of 0.88 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.63 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(82\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0591113520

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 1.3 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.94 mmHg. They will test using \(\alpha = 0.04\).

1. In a sample of size \(97\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0659845458

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 147 mmHg. They want to be able to detect a true average blood pressure change of 3.46 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.08 mmHg. They will test using \(\alpha = 0.12\).

1. In a sample of size \(51\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0695852975

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 135 mmHg. They want to be able to detect a true average blood pressure change of 1.57 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.7 mmHg. They will test using \(\alpha = 0.17\).

1. In a sample of size \(38\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0522251972

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 137 mmHg. They want to be able to detect a true average blood pressure change of 0.98 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.52 mmHg. They will test using \(\alpha = 0.19\).

1. In a sample of size \(76\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0358711913

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 1.19 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.31 mmHg. They will test using \(\alpha = 0.19\).

1. In a sample of size \(100\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0043927324

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 143 mmHg. They want to be able to detect a true average blood pressure change of 1.31 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.51 mmHg. They will test using \(\alpha = 0.14\).

1. In a sample of size \(71\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.92\)?

Question ID: 0271058282

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 149 mmHg. They want to be able to detect a true average blood pressure change of 0.78 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 7.02 mmHg. They will test using \(\alpha = 0.19\).

1. In a sample of size \(66\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0950992139

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 136 mmHg. They want to be able to detect a true average blood pressure change of 1.28 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.52 mmHg. They will test using \(\alpha = 0.2\).

1. In a sample of size \(38\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.87\)?

Question ID: 0997349443

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 133 mmHg. They want to be able to detect a true average blood pressure change of 1.54 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.23 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(81\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0363095710

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 2.67 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.61 mmHg. They will test using \(\alpha = 0.02\).

1. In a sample of size \(80\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0248248677

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 2.11 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.59 mmHg. They will test using \(\alpha = 0.05\).

1. In a sample of size \(57\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0997326373

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 130 mmHg. They want to be able to detect a true average blood pressure change of 1.01 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 13.05 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(98\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0204424889

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 134 mmHg. They want to be able to detect a true average blood pressure change of 2.91 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.77 mmHg. They will test using \(\alpha = 0.18\).

1. In a sample of size \(82\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0536259197

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 140 mmHg. They want to be able to detect a true average blood pressure change of 0.74 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.49 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(90\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.81\)?

Question ID: 0931934289

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 1.09 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.02 mmHg. They will test using \(\alpha = 0.15\).

1. In a sample of size \(41\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0118483929

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 1.99 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.84 mmHg. They will test using \(\alpha = 0.09\).

1. In a sample of size \(43\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.93\)?

Question ID: 0436258207

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 149 mmHg. They want to be able to detect a true average blood pressure change of 1.03 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.84 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(57\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0429137107

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 140 mmHg. They want to be able to detect a true average blood pressure change of 0.91 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.42 mmHg. They will test using \(\alpha = 0.09\).

1. In a sample of size \(97\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0954291561

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 147 mmHg. They want to be able to detect a true average blood pressure change of 1.44 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.12 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(46\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0132130435

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 0.47 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.7 mmHg. They will test using \(\alpha = 0.11\).

1. In a sample of size \(62\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.81\)?

Question ID: 0171518094

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 146 mmHg. They want to be able to detect a true average blood pressure change of 0.75 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 6.59 mmHg. They will test using \(\alpha = 0.07\).

1. In a sample of size \(71\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0483501928

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 141 mmHg. They want to be able to detect a true average blood pressure change of 2.19 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 11.4 mmHg. They will test using \(\alpha = 0.06\).

1. In a sample of size \(43\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.94\)?

Question ID: 0176866453

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 150 mmHg. They want to be able to detect a true average blood pressure change of 3.21 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 14.41 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(47\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.95\)?

Question ID: 0288237549

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 0.97 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.5 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(92\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.91\)?

Question ID: 0304638472

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 134 mmHg. They want to be able to detect a true average blood pressure change of 1.57 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 12.22 mmHg. They will test using \(\alpha = 0.08\).

1. In a sample of size \(64\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.82\)?

Question ID: 0584388706

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 140 mmHg. They want to be able to detect a true average blood pressure change of 1.13 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 10.91 mmHg. They will test using \(\alpha = 0.03\).

1. In a sample of size \(86\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.86\)?

Question ID: 0612682973

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 0.8 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.05 mmHg. They will test using \(\alpha = 0.1\).

1. In a sample of size \(69\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.9\)?

Question ID: 0777799004

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 138 mmHg. They want to be able to detect a true average blood pressure change of 0.62 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 5.74 mmHg. They will test using \(\alpha = 0.06\).

1. In a sample of size \(52\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.89\)?

Question ID: 0060147872

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 131 mmHg. They want to be able to detect a true average blood pressure change of 0.9 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 8.54 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(64\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.85\)?

Question ID: 0187901995

Researchers are investigating the impact that a new drug has on blood pressure. They want to conduct a clinical trial to test if the drug is effective. The current average systolic blood pressure in the target population is 145 mmHg. They want to be able to detect a true average blood pressure change of 0.81 mmHg. Assume the population standard deviation of systolic blood pressure is known to be 9.34 mmHg. They will test using \(\alpha = 0.16\).

1. In a sample of size \(71\), what is the power of the test at detecting the desired differences?
2. What is the approximate sample size required in order to achieve a power of \(0.83\)?

Question ID: 0297206120

Self Assessment 15.14

A hypothesis test is run, testing \(H_0: \lambda = 98.2838\). The estimated value for \(\lambda\), based on the sample, is 90.6691. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.12, and that the hypothesis test is run with a significance level of 0.053.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda \geq 98.2838\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda \geq 98.2838\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 98.2838\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 98.2838\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0490376999

A hypothesis test is run, testing \(H_0: \rho \leq 30.9976\). The estimated value for \(\rho\), based on the sample, is 41.105. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.053, and that the hypothesis test is run with a significance level of 0.235.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 30.9976\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 30.9976\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho = 30.9976\)?
4. What is the conclusion that would be reached testing \(H_0: \rho = 30.9976\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0192088517

A hypothesis test is run, testing \(H_0: \mu = 62.3635\). The estimated value for \(\mu\), based on the sample, is 6.503. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.051, and that the hypothesis test is run with a significance level of 0.006.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu \geq 62.3635\)?
2. What is the conclusion that would be reached testing \(H_0: \mu \geq 62.3635\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu \leq 62.3635\)?
4. What is the conclusion that would be reached testing \(H_0: \mu \leq 62.3635\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0202109023

A hypothesis test is run, testing \(H_0: \theta \geq 15.1635\). The estimated value for \(\theta\), based on the sample, is 26.3035. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.883, and that the hypothesis test is run with a significance level of 0.107.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta = 15.1635\)?
2. What is the conclusion that would be reached testing \(H_0: \theta = 15.1635\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 15.1635\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 15.1635\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0863357136

A hypothesis test is run, testing \(H_0: \rho = 92.8381\). The estimated value for \(\rho\), based on the sample, is 97.2039. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.098, and that the hypothesis test is run with a significance level of 0.172.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 92.8381\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 92.8381\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 92.8381\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 92.8381\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0568434262

A hypothesis test is run, testing \(H_0: \rho \leq 60.0177\). The estimated value for \(\rho\), based on the sample, is 14.6153. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.884, and that the hypothesis test is run with a significance level of 0.117.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 60.0177\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 60.0177\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho = 60.0177\)?
4. What is the conclusion that would be reached testing \(H_0: \rho = 60.0177\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0414384443

A hypothesis test is run, testing \(H_0: \sigma \geq 53.3549\). The estimated value for \(\sigma\), based on the sample, is 61.2125. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.97, and that the hypothesis test is run with a significance level of 0.015.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 53.3549\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma = 53.3549\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 53.3549\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 53.3549\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0259201640

A hypothesis test is run, testing \(H_0: \gamma = 20.4867\). The estimated value for \(\gamma\), based on the sample, is 5.5158. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.103, and that the hypothesis test is run with a significance level of 0.108.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma \geq 20.4867\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma \geq 20.4867\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma \leq 20.4867\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma \leq 20.4867\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0257169422

A hypothesis test is run, testing \(H_0: \theta = 35.9791\). The estimated value for \(\theta\), based on the sample, is 26.8065. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.085, and that the hypothesis test is run with a significance level of 0.022.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta \geq 35.9791\)?
2. What is the conclusion that would be reached testing \(H_0: \theta \geq 35.9791\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 35.9791\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 35.9791\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0133443581

A hypothesis test is run, testing \(H_0: \sigma \geq 34.6909\). The estimated value for \(\sigma\), based on the sample, is 32.2627. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.031, and that the hypothesis test is run with a significance level of 0.091.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 34.6909\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma = 34.6909\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 34.6909\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 34.6909\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0586525208

A hypothesis test is run, testing \(H_0: \lambda \geq 15.6488\). The estimated value for \(\lambda\), based on the sample, is 30.0006. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.985, and that the hypothesis test is run with a significance level of 0.197.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 15.6488\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda = 15.6488\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 15.6488\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 15.6488\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0692907816

A hypothesis test is run, testing \(H_0: \sigma \leq 27.955\). The estimated value for \(\sigma\), based on the sample, is 55.0215. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.106, and that the hypothesis test is run with a significance level of 0.226.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma \geq 27.955\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma \geq 27.955\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 27.955\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma = 27.955\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0602471221

A hypothesis test is run, testing \(H_0: \rho \geq 77.5462\). The estimated value for \(\rho\), based on the sample, is 120.8726. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.862, and that the hypothesis test is run with a significance level of 0.081.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho = 77.5462\)?
2. What is the conclusion that would be reached testing \(H_0: \rho = 77.5462\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 77.5462\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 77.5462\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0906695645

A hypothesis test is run, testing \(H_0: \gamma \geq 77.8206\). The estimated value for \(\gamma\), based on the sample, is 13.2639. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.13, and that the hypothesis test is run with a significance level of 0.292.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma = 77.8206\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma = 77.8206\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma \leq 77.8206\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma \leq 77.8206\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0374980621

A hypothesis test is run, testing \(H_0: \rho \leq 32.0055\). The estimated value for \(\rho\), based on the sample, is 43.5567. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.135, and that the hypothesis test is run with a significance level of 0.177.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 32.0055\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 32.0055\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho = 32.0055\)?
4. What is the conclusion that would be reached testing \(H_0: \rho = 32.0055\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0023513957

A hypothesis test is run, testing \(H_0: \rho = 17.0921\). The estimated value for \(\rho\), based on the sample, is 3.4566. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.043, and that the hypothesis test is run with a significance level of 0.165.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 17.0921\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 17.0921\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 17.0921\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 17.0921\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0735072126

A hypothesis test is run, testing \(H_0: \rho = 74.4705\). The estimated value for \(\rho\), based on the sample, is 71.6325. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.133, and that the hypothesis test is run with a significance level of 0.262.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 74.4705\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 74.4705\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 74.4705\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 74.4705\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0853591782

A hypothesis test is run, testing \(H_0: \sigma = 67.9343\). The estimated value for \(\sigma\), based on the sample, is 62.4194. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.043, and that the hypothesis test is run with a significance level of 0.021.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma \geq 67.9343\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma \geq 67.9343\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 67.9343\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 67.9343\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0948648203

A hypothesis test is run, testing \(H_0: \sigma \leq 29.4727\). The estimated value for \(\sigma\), based on the sample, is 4.6598. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.878, and that the hypothesis test is run with a significance level of 0.244.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma \geq 29.4727\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma \geq 29.4727\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 29.4727\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma = 29.4727\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0633349976

A hypothesis test is run, testing \(H_0: \gamma = 68.1696\). The estimated value for \(\gamma\), based on the sample, is 59.2343. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.105, and that the hypothesis test is run with a significance level of 0.237.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma \geq 68.1696\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma \geq 68.1696\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma \leq 68.1696\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma \leq 68.1696\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0800170934

A hypothesis test is run, testing \(H_0: \sigma \leq 19.0524\). The estimated value for \(\sigma\), based on the sample, is 16.8693. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.934, and that the hypothesis test is run with a significance level of 0.299.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma \geq 19.0524\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma \geq 19.0524\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 19.0524\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma = 19.0524\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0213224348

A hypothesis test is run, testing \(H_0: \theta \geq 69.168\). The estimated value for \(\theta\), based on the sample, is 27.3222. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.035, and that the hypothesis test is run with a significance level of 0.037.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta = 69.168\)?
2. What is the conclusion that would be reached testing \(H_0: \theta = 69.168\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 69.168\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 69.168\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0522919556

A hypothesis test is run, testing \(H_0: \mu \leq 72.1159\). The estimated value for \(\mu\), based on the sample, is 2.5692. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.865, and that the hypothesis test is run with a significance level of 0.052.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu \geq 72.1159\)?
2. What is the conclusion that would be reached testing \(H_0: \mu \geq 72.1159\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu = 72.1159\)?
4. What is the conclusion that would be reached testing \(H_0: \mu = 72.1159\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0456815123

A hypothesis test is run, testing \(H_0: \lambda \geq 65.0747\). The estimated value for \(\lambda\), based on the sample, is 31.4702. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.126, and that the hypothesis test is run with a significance level of 0.006.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 65.0747\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda = 65.0747\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 65.0747\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 65.0747\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0780532724

A hypothesis test is run, testing \(H_0: \theta \geq 95.9069\). The estimated value for \(\theta\), based on the sample, is 68.7282. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.042, and that the hypothesis test is run with a significance level of 0.113.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta = 95.9069\)?
2. What is the conclusion that would be reached testing \(H_0: \theta = 95.9069\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 95.9069\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 95.9069\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0761234194

A hypothesis test is run, testing \(H_0: \lambda \geq 54.4161\). The estimated value for \(\lambda\), based on the sample, is 17.2833. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.114, and that the hypothesis test is run with a significance level of 0.019.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 54.4161\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda = 54.4161\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 54.4161\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 54.4161\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0458517663

A hypothesis test is run, testing \(H_0: \mu = 3.7715\). The estimated value for \(\mu\), based on the sample, is 5.5564. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.083, and that the hypothesis test is run with a significance level of 0.017.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu \geq 3.7715\)?
2. What is the conclusion that would be reached testing \(H_0: \mu \geq 3.7715\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu \leq 3.7715\)?
4. What is the conclusion that would be reached testing \(H_0: \mu \leq 3.7715\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0554174129

A hypothesis test is run, testing \(H_0: \mu \leq 96.6436\). The estimated value for \(\mu\), based on the sample, is 61.4589. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.946, and that the hypothesis test is run with a significance level of 0.161.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu \geq 96.6436\)?
2. What is the conclusion that would be reached testing \(H_0: \mu \geq 96.6436\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu = 96.6436\)?
4. What is the conclusion that would be reached testing \(H_0: \mu = 96.6436\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0890724006

A hypothesis test is run, testing \(H_0: \lambda \geq 36.1536\). The estimated value for \(\lambda\), based on the sample, is 28.5613. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.054, and that the hypothesis test is run with a significance level of 0.012.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 36.1536\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda = 36.1536\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 36.1536\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 36.1536\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0096465948

A hypothesis test is run, testing \(H_0: \lambda = 48.7793\). The estimated value for \(\lambda\), based on the sample, is 50.011. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.028, and that the hypothesis test is run with a significance level of 0.222.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda \geq 48.7793\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda \geq 48.7793\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 48.7793\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 48.7793\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0659932357

A hypothesis test is run, testing \(H_0: \mu \geq 51.4967\). The estimated value for \(\mu\), based on the sample, is 57.7079. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.914, and that the hypothesis test is run with a significance level of 0.058.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu = 51.4967\)?
2. What is the conclusion that would be reached testing \(H_0: \mu = 51.4967\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu \leq 51.4967\)?
4. What is the conclusion that would be reached testing \(H_0: \mu \leq 51.4967\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0966511190

A hypothesis test is run, testing \(H_0: \sigma = 13.9193\). The estimated value for \(\sigma\), based on the sample, is 25.7591. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.008, and that the hypothesis test is run with a significance level of 0.178.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma \geq 13.9193\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma \geq 13.9193\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 13.9193\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 13.9193\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0013413747

A hypothesis test is run, testing \(H_0: \sigma \geq 26.9234\). The estimated value for \(\sigma\), based on the sample, is 33.9791. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.879, and that the hypothesis test is run with a significance level of 0.309.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 26.9234\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma = 26.9234\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 26.9234\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 26.9234\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0960958418

A hypothesis test is run, testing \(H_0: \gamma = 67.2374\). The estimated value for \(\gamma\), based on the sample, is 50.0571. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.027, and that the hypothesis test is run with a significance level of 0.068.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma \geq 67.2374\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma \geq 67.2374\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma \leq 67.2374\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma \leq 67.2374\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0570631732

A hypothesis test is run, testing \(H_0: \gamma \leq 90.9304\). The estimated value for \(\gamma\), based on the sample, is 14.9194. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.864, and that the hypothesis test is run with a significance level of 0.245.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma \geq 90.9304\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma \geq 90.9304\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma = 90.9304\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma = 90.9304\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0942406898

A hypothesis test is run, testing \(H_0: \lambda = 7.1507\). The estimated value for \(\lambda\), based on the sample, is 6.8843. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.11, and that the hypothesis test is run with a significance level of 0.125.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda \geq 7.1507\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda \geq 7.1507\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 7.1507\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 7.1507\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0637021880

A hypothesis test is run, testing \(H_0: \theta \leq 72.5068\). The estimated value for \(\theta\), based on the sample, is 62.3221. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.951, and that the hypothesis test is run with a significance level of 0.042.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta \geq 72.5068\)?
2. What is the conclusion that would be reached testing \(H_0: \theta \geq 72.5068\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta = 72.5068\)?
4. What is the conclusion that would be reached testing \(H_0: \theta = 72.5068\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0232815268

A hypothesis test is run, testing \(H_0: \rho = 90.8699\). The estimated value for \(\rho\), based on the sample, is 64.5141. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.085, and that the hypothesis test is run with a significance level of 0.1.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 90.8699\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 90.8699\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 90.8699\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 90.8699\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0374745493

A hypothesis test is run, testing \(H_0: \lambda = 22.4183\). The estimated value for \(\lambda\), based on the sample, is 39.3941. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.06, and that the hypothesis test is run with a significance level of 0.293.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda \geq 22.4183\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda \geq 22.4183\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 22.4183\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 22.4183\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0696771719

A hypothesis test is run, testing \(H_0: \mu = 61.3451\). The estimated value for \(\mu\), based on the sample, is 67.9385. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.048, and that the hypothesis test is run with a significance level of 0.005.

1. What is the \(p\)-value that would be observed testing \(H_0: \mu \geq 61.3451\)?
2. What is the conclusion that would be reached testing \(H_0: \mu \geq 61.3451\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \mu \leq 61.3451\)?
4. What is the conclusion that would be reached testing \(H_0: \mu \leq 61.3451\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0491966469

A hypothesis test is run, testing \(H_0: \sigma \geq 73.2664\). The estimated value for \(\sigma\), based on the sample, is 48.8381. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.11, and that the hypothesis test is run with a significance level of 0.026.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 73.2664\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma = 73.2664\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 73.2664\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 73.2664\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0349151302

A hypothesis test is run, testing \(H_0: \gamma \geq 53.1179\). The estimated value for \(\gamma\), based on the sample, is 84.5573. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.906, and that the hypothesis test is run with a significance level of 0.104.

1. What is the \(p\)-value that would be observed testing \(H_0: \gamma = 53.1179\)?
2. What is the conclusion that would be reached testing \(H_0: \gamma = 53.1179\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \gamma \leq 53.1179\)?
4. What is the conclusion that would be reached testing \(H_0: \gamma \leq 53.1179\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0961635688

A hypothesis test is run, testing \(H_0: \lambda \geq 97.8208\). The estimated value for \(\lambda\), based on the sample, is 24.1665. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.038, and that the hypothesis test is run with a significance level of 0.127.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 97.8208\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda = 97.8208\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda \leq 97.8208\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda \leq 97.8208\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0267049355

A hypothesis test is run, testing \(H_0: \rho = 88.4338\). The estimated value for \(\rho\), based on the sample, is 61.1972. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.071, and that the hypothesis test is run with a significance level of 0.067.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 88.4338\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 88.4338\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 88.4338\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 88.4338\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0224691063

A hypothesis test is run, testing \(H_0: \rho = 56.621\). The estimated value for \(\rho\), based on the sample, is 37.7867. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.068, and that the hypothesis test is run with a significance level of 0.025.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho \geq 56.621\)?
2. What is the conclusion that would be reached testing \(H_0: \rho \geq 56.621\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 56.621\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 56.621\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0147494081

A hypothesis test is run, testing \(H_0: \theta = 41.2683\). The estimated value for \(\theta\), based on the sample, is 34.1333. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.106, and that the hypothesis test is run with a significance level of 0.147.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta \geq 41.2683\)?
2. What is the conclusion that would be reached testing \(H_0: \theta \geq 41.2683\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 41.2683\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 41.2683\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0592317914

A hypothesis test is run, testing \(H_0: \sigma \geq 46.988\). The estimated value for \(\sigma\), based on the sample, is 86.5701. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.897, and that the hypothesis test is run with a significance level of 0.253.

1. What is the \(p\)-value that would be observed testing \(H_0: \sigma = 46.988\)?
2. What is the conclusion that would be reached testing \(H_0: \sigma = 46.988\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \sigma \leq 46.988\)?
4. What is the conclusion that would be reached testing \(H_0: \sigma \leq 46.988\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0592318412

A hypothesis test is run, testing \(H_0: \lambda \leq 56.8683\). The estimated value for \(\lambda\), based on the sample, is 20.0169. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.857, and that the hypothesis test is run with a significance level of 0.109.

1. What is the \(p\)-value that would be observed testing \(H_0: \lambda \geq 56.8683\)?
2. What is the conclusion that would be reached testing \(H_0: \lambda \geq 56.8683\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \lambda = 56.8683\)?
4. What is the conclusion that would be reached testing \(H_0: \lambda = 56.8683\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0308901834

A hypothesis test is run, testing \(H_0: \theta \geq 41.2758\). The estimated value for \(\theta\), based on the sample, is 37.1224. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.05, and that the hypothesis test is run with a significance level of 0.004.

1. What is the \(p\)-value that would be observed testing \(H_0: \theta = 41.2758\)?
2. What is the conclusion that would be reached testing \(H_0: \theta = 41.2758\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \theta \leq 41.2758\)?
4. What is the conclusion that would be reached testing \(H_0: \theta \leq 41.2758\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0988035318

A hypothesis test is run, testing \(H_0: \rho \geq 81.6801\). The estimated value for \(\rho\), based on the sample, is 110.2073. The hypothesis is tested using a symmetric null distribution. Suppose that the \(p\)-value is found to be 0.912, and that the hypothesis test is run with a significance level of 0.166.

1. What is the \(p\)-value that would be observed testing \(H_0: \rho = 81.6801\)?
2. What is the conclusion that would be reached testing \(H_0: \rho = 81.6801\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

3. What is the \(p\)-value that would be observed testing \(H_0: \rho \leq 81.6801\)?
4. What is the conclusion that would be reached testing \(H_0: \rho \leq 81.6801\)?

Based on the results, we can reject the null hypothesis.Based on the results, we fail to reject the null hypothesis.

Question ID: 0833161518

---

1. For instance, if you are considering a treatment, you should assume that the treatment has no effect. This way, without strong evidence suggesting that there is an effect, you will not use the treatment. The same ideas apply more broadly.

2. Note, many sources will list the null hypothesis as simply \(H_0: \theta = \theta_0\) and control the tail behaviour exclusively via the alternative. This results in the same test mechanism but is, in my opinion, less clear as to the actual hypotheses that are being tested.

3. The use of a one-tailed test should be reserved for cases where there is no real possibility of contradicting the null in both directions.

4. and, indeed, of any procedure that deals with randomness and uncertainty

5. Uncertainty ensures us that there is always a chance that the null hypothesis was incorrectly rejected.

6. Recall that statistics are any quantities that can be computed given a sample of data.

7. Here, extreme means contradictory to the null hypothesis. Note that the extremity of an observation depends on whether we have a one-tailed or two-tailed alternative. With a two-tailed alternative, we need to consider extreme values in both tails, with a one-tailed alternative, we simply need to consider values that are further away from the null value.

8. Such as the normal, or the \(t\) distributions, which are both quite common.

9. Or, equivalently, if the test statistic is larger in magnitude than the critical value.

10. Unhelpfully…

11. This is challenging for several reasons. One is that the test statistic is defined so that it has a well-defined null distribution. Unfortunately, to work out the type II error probability, the null distribution is not helpful. Instead, we need to work out the distribution of the test statistic assuming the null is not true. Unfortunately, the alternative is typically a composite hypothesis. That is, the alternative is specified as a range of possible values, rather than a single point. If the alternative is \(H_A: \mu \neq 0\), should we take \(\mu = 1\) or \(\mu = -1\) or \(\mu = \pi\)? It is not always clear. As a result, we tend to define the probability of a type II error on the basis of a function, say \(\pi'(\theta)\) that gives the probability of a false negative for any given value \(\theta\).

12. From the binomial we can justify the equivalent conclusion by first considering the normal approximation to the binomial, and then scaling the results as required.

13. For some significance level, \(\alpha\).

14. The concept of a straw man stems from the world of debate wherein sometimes individuals argue against a position that others do not really hold. The idea is that there is a position that is constructed that appears to be the one up for debate, but that is actually different in important ways. The person is then said to be attacking a straw man, as in, a human figure made of straw that would be easy to knock over or destroy.

15. Consider a researcher performing \(n\) independent hypothesis tests, each at a significance level of \(p\). Note that the number of results they would expect to find as statistically significant, even if none of them truly are, follows a \(\text{Bin}(n, p)\) distribution. If \(p = 0.05\), then after \(n=14\) tests there is a greater than \(50\%\) chance that at least one of them returns a statistically significant result, despite none being true.