3  The Core Concepts of Probability

3.1 Assigning Probabilities (and The Equally Likely Outcome Model)

There are a plethora of ways to assign probabilities to different events. At the most basic level any rule that maps from the space of possible events to real numbers between \(0\) and \(1\) can be used as rules for probability assignment. That is, probability assignment is a set of rules which says “for this event assign this probability.”

Example 3.1 (Coin Toss Probabilities) Suppose that the fair coin used by Charles and Sadie is tossed one time. Write down the probability assignments relating to this experiment.

Solution

In this case we have \(\mathcal{S} = \{\text{H},\text{T}\}\). Thus, the possible events for which we need to assign probabilities are \(\emptyset\), \(\{\text{H}\}\), \(\{\text{T}\}\), and \(\{\text{H},\text{T}\} = \mathcal{S}\). For any probability model we have \(P(\emptyset) = 0\) and \(P(\mathcal{S}) = 1\). When we say that a coin is “fair” we are saying that \(P(\text{T}) = P(\text{H})\), and since these are the only two possible outcomes in the sample space, we must have that they each have probability \(0.5\).

Not every assignment of probability values is going to be valid. Suppose, for instance, that we have a six-sided die, each side labelled with a number from one to six. If I told you that there was a probability of \(0.5\) that it comes up \(1\), \(0.5\) that it comes up \(2\), \(0.5\) that it comes up \(3\), \(0.5\) that it comes up \(4\), \(0.5\) that it comes up \(5\), and \(0.5\) that it comes up \(6\), you would probably call me a liar.¹ If, as we have previously seen, probabilities represent the long run proportion of time that a particular event is observed, we cannot have \(6\) different outcomes each occurring in half of all cases.

Beyond the restrictions that we impose to form “valid” probability rules, we have another concern: scalability. It is perfectly acceptable to indicate that in an experiment with \(3\) outcomes, the first has a probability of \(0.25\), the second of \(0.3\), and the third of \(0.45\). What if the experiment has \(100\) possible outcomes? Or \(1000\)? It quickly becomes apparent that enumerating the probabilities of each event in the sample space is not an efficient way of assigning probabilities in practice. A core focus of our study of probability will be finding techniques that allow us to efficiently encode probability information into manageable objects. Once we have done this we will be in a position where we can manipulate these (comparatively) simple mathematical quantities in order to make statements and conclusions about any of the events of interest, even if they have never been explicitly outlined as having an assigned probability.

While we will consider myriad methods for accomplishing these goals throughout our study of probability, we begin with a very useful model which simplifies probability assignment, without any added complexity, and creates a solid foundation for us to explore the properties of probability models. We start by considering equally likely outcomes. As the name suggests, the probability model considering equally likely outcomes assigns an equal probability to every possible outcome of the experiment. This is a probability model that we are already distinctly familiar with: flipping a coin, rolling a die, or drawing a card are all examples of experiments which rely on the equally likely outcomes framework.

Remark (Statisticians and Urn Models). In statistics and probability courses and books you will often have instructors or authors using fairly simple models to illustrate probability concepts. There will often be questions relating to coin tosses, and dice, and decks of cards, and everyone’s favourite: urns. It will very frequently be the case that a statistics question will state that there is an urn with some combination of coloured balls within it, from which you will be selecting some number either with or without replacement. The frequency of these types of examples and questions often feels disconnected from the refrain that “uncertainty is all around us” and that “statistics is relevant to every aspect of our world!”² Why is it that we seldom see questions or examples that are directly tied to these wide spread applications of the lessons and techniques being taught?

In part these simple experiments are cleaner to handle than “real world” situations. We can easily assume that a die is fair and that takes care of any unsuspecting wrinkles that will necessarily come along with the “real world”. This is not dissimilar to working under the assumption of frictionless surfaces in introductory physics, or assuming that human beings are rational in economics. Another key point is that most of us have deep familiarity with dice, and coins, and cards.³ The same is not going to be true of stories that are derived from different use cases in the real world. A final important point, and this will be something we see in depth in the coming chapters, is that from a statistical point of view: there is no difference. Once we have the tools to work with these quantities, we have the tools to work with any of the quantities. This actually distinguishes the use of these types of examples in statistics and probability from those for other subjects: at no point is anything that we are learning incorrect, or overly simple - we are just focusing on the raw probabilistic nature of the phenomenon. As a result, we will continue to see these simple models in these notes. I would encourage you, whenever possible, to hold a topic in mind that matters more to you and start trying to draw the parallels between rolling dice, and whatever it is that you may care about.

Why urns, specifically? Well, whether it be coin flipping or dice rolling or card selection, we can model this equivalently using an urn (with \(2\), \(6\), and \(52\) items, respectively). The urn becomes more flexible to exactly dictate what the probability of any selection will be, which is a useful way of moving from equally likely models (each ball is equally likely to be selected) to arbitrary models (we can have however many identical balls in the urn as we would like).

If we have an experiment with a sample space \(\mathcal{S}\) which has \(|\mathcal{S}| = k\) total elements⁴, then each element of the sample space occurs with probability \(\dfrac{1}{k}\). In the case of the coin toss example, \(\mathcal{S} = \{\text{H}, \text{T}\}\), and so \(k=2\) and each outcome occurs with probability \(\dfrac{1}{2}\). In the case of drawing a card at random, there are \(52\) different outcomes, and so \(k=52\), and the probability of drawing any particular card is \(\dfrac{1}{52}\).

It is critically important to recognize that the equal probability model assigns equal likelihood to the possible outcomes of an experiment, not the possible events of interest. It will not be the case that all events have the same probability. To make this concrete, consider the events \(A\) “the ace of spades is drawn” and \(B\) “any spade is drawn”. It is clear that \(B\) happens more frequently than \(A\), even though we have said that this is an experiment with equally likely outcomes. Remember: an outcome is an observation from a single experimental run, an event is any collection of these possible outcomes.

A core goal is then bridging the gap between the probability of an outcome⁵ and the probability of an event. In order to do so, we will next consider the rules of probability, introducing properties that are required for valid probability assignments, and the techniques for manipulating probabilities to calculate the probabilities of quantities of interest.

3.1.1 Using R for the Equally Likely Probability Model

In the previous chapter we saw how we can codify sample spaces and events using vectors in R. In the introduction we actually saw how we can sample from a sample space using the equally likely outcome framework. Specifically, an application of the sample function will draw a set number of values from a sample space, giving each value an equal probability to be drawn.⁶

3.2 The Axioms of Probability

We have previously seen that not every probability assignment can be valid. For instance, assigning \(0.5\) probability to each outcome on a die leads to a nonsensical scenario. With just a little imagination, we can conjure equally nonsensical scenarios in other ways. For instance, it would make very little sense to discuss the probability of an event being a negative value. What would it mean for an event to occur in a negative proportion of experimental runs? Alternatively, we can consider two events that are nested in one another: say event \(A\) is that we draw the ace of spades, and event \(B\) is that we draw any spade. Every single time that \(A\) happens, we know that \(B\) also happens. But there are ways that \(B\) can occur where \(A\) does not.⁷ If I told you the probability of \(A\) was \(0.5\) and the probability of \(B\) was \(0.2\), this would violate our base instincts. How can it be more likely to draw the ace of spades than it would be to draw any spade at all?⁸

Often in mathematics when we have an intuitive set of rules⁹ that particular quantities must obey, we work to add formality through defining properties of these concepts. To this end, we can define the key properties that probabilities must obey in order to be well-defined, valid probabilities. With three fairly basic properties, we can completely specify what must be true in order for a set of probabilities to be “valid”, and to in turn align with our intuitions.

The Axioms of Probability

1. Unitary: Every valid set of probabilities must assign a probability of \(1\) to the full sample space. That is, \(P(\mathcal{S}) = 1\). This is an intuitive requirement as every time the experiment is run we observe an outcome in the sample space. As a result, in every experimental run the event \(\mathcal{S}\) occurs.
2. Non-negative: We require that every probability is non-negative. We can have probabilities of \(0\), but we can never have a probability less than zero. Again, this is sensible¹⁰ but is important to include in our formalization. Specifically, for every event \(E\), we must have \(P(E) \geq 0\).
3. Additivity: the final property requires slightly more parsing on first pass. Suppose that we define a sequence of events, \(E_1, E_2, E_3, \dots\) such that no two events have any overlap. That is, \(E_j \cap E_\ell = \emptyset\) for all \(\ell\neq j\). Then, the final property we require for probabilities is that \[P(E_1 \cup E_2 \cup E_3 \cup \cdots) = P\left(\bigcup_i E_i\right) = \sum_i P(E_i) = P(E_1) + P(E_2) + P(E_3) + \cdots.\] That is, the probability of the union of disjoint events is the summation of the probability of these events.

It is worth dwelling slightly on axiom 3. Consider the case of drawing a card at random from a deck of \(52\) cards. Using the equally likely outcome model for probability we know that the probability that any card is drawn is given by \(\dfrac{1}{52}\). If I were to ask “what is the probability you draw that ace of spades?” under this model you can respond, immediately, with \(\dfrac{1}{52}\). Now, if I were to ask “what is the probability that you draw the ace of spades or the two of spades?” then intuitively you likely figure that this will be \(\dfrac{2}{52}\). Note that the event \(E_1\), “draw the ace of spades” and the event \(E_2\) “draw the two of spades”, are disjoint events. Moreover, recall that the union is the “or” and so \(E_1\cup E_2\) is the same as \(E_1\) or \(E_2\). Taken together then, \[P(E_1\cup E_2) = P(E_1) + P(E_2).\] The axiom of additivity extends this intuition to an arbitrary number of events.

Example 3.2 (Basic Additivity) Still unsure of how best to go about using cards to replace their coin game, Charles and Sadie are considering various different events and trying to understand their probabilistic behaviour. They take \(S\), \(C\), \(H\), and \(D\) to be the events that a spade, club, heart, or diamond are drawn from a standard deck of cards, respectively. Further, they take \(C_j\) to be the event that a card with denomination \(j\) is drawn (\(j\) ranging from ace with \(1\) through King with \(13\)). If they consider the union of any two (or more) of these events when can they leverage properties of additivity? When can’t they?

Solution

In order to use the properties of additivity it is required that the two events are disjoint. Note that taking any two (or more) of \(S\), \(C\), \(H\), and \(D\) will lead to disjoint events. There is no way to draw a card which has two suits on it at once. Similarly, taking any two (or more) of \(C_j\) will lead to disjoint events. However, mixing any of the suited events (\(S\), \(C\), \(H\), and \(D\)) with any \(C_j\) will not be disjoint.

Consider \(S\cap C_1\). The ace of spades is in \(S\) since it is a spade and it is in \(C_1\) since it is an ace. As a result, \(S\cap C_1 = \{\text{Ace of Spades}\}\). Because of this we are not able to say that \(P(A \cup C_1) = P(A) + P(C_1)\). However, we can say that \[P(S\cup C\cup H\cup D) = P(S) + P(C) + P(H) + P(D),\] and could do the same with any subset of these sets. Similarly, we can take \[P\left(\bigcup_{j=1}^{13} C_j\right) = \sum_{j=1}^{13} P(C_j),\] or any of the subsets there.

These three axioms fully define valid probabilities. Any mechanism that assigns probability values to events which conform to these rules will assign valid probabilities. While it may seem counterintuitive that such basic rules fully define our notion of a probability, these rules readily give rise to many other properties that are very useful when working with probabilities.

3.3 Secondary Properties of Probabilities

Using the previously indicated axioms of probability we are able to derive many useful secondary properties. These properties will frequently be used to actually compute different probabilities, and are helpful to become familiar with. All of the following properties follow directly from the axioms, though, some are more clear than others. For the following we take \(E\) and \(E_1,E_2,E_3,\dots\) to be arbitrary events on some well defined sample space.

1. Complements: \(P(E^C) = 1-P(E)\), and equivalently, \(P(E) = 1 - P(E^C)\).
2. Null Event: \(P(\emptyset) = 0\).
3. Arbitrary Unions (Two Events): \(P(E_1 \cup E_2) = P(E_1) + P(E_2) - P(E_1\cap E_2)\).
4. Arbitrary Unions (Three Events): \[\begin{multline*}P(E_1 \cup E_2 \cup E_3) = P(E_1) + P(E_2) + P(E_3) - P(E_1\cap E_2) - P(E_1 \cap E_3) \\ - P(E_2 \cap E_3) + P(E_1 \cap E_2 \cap E_3).\end{multline*}\]
5. Containment: If \(E_1 \subseteq E_2\) then \(P(E_1) \leq P(E_2)\).

Proofs of the Secondary Properties of Probability

It may be instructive to see how these properties are derived. Doing so generates added familiarity with manipulating probability expressions and helps to encourage deeper understanding.

1. Note that, for any event \(E\), by definition we have \(E \cup E^C = \mathcal{S}\) and \(E \cap E^C = \emptyset\). As a result, we can apply additivity to the sets \(E\) and \(E^C\) giving \(P(E \cup E^C) = P(E) + P(E^C)\). However, since \(E\cup E^C = \mathcal{S}\), then we know that \(P(E \cup E^C) = P(\mathcal{S}) = 1\) by the unitary property. Taken together this tells us that \(1 = P(E) + P(E^C)\), and rearranging gives \(P(E^C) = 1 - P(E)\), or \(P(E) = 1 - P(E^C)\), as required.

2. We know that \(\mathcal{S}^C = \emptyset\). Using secondary property (1), \(P(E) = 1 - P(E^C)\). Taking \(E = \emptyset\) gives \(P(\emptyset) = 1 - P(\mathcal{S}) = 1 - 1 = 0\), by the unitary property.

3. Here note that \(E_1 \cup E_2\) can be written as \(E_1 \cup E_2'\) where \(E_2' = E_2\cap E_1^C\). That is, \(E_2'\) contains the outcomes from \(E_2\) which were not shared by \(E_1\). Then \(E_1 \cap E_2' = \emptyset\) so we can write \(P(E_1 \cup E_2) = P(E_1 \cup E_2') = P(E_1) + P(E_2')\), by additivity. Now, if we define \(E_2^* = E_2\cap E_1\) then \(E_2 = E_2' \cup E_2^*\), and \(E_2'\cap E_2^* = \emptyset\). Thus, \(P(E_2) = P(E_2'\cup E_2^*) = P(E_2') + P(E_2^*)\). Rearranging this gives \(P(E_2') = P(E_2) - P(E_2^*)\), and we know that \(P(E_2^*) = P(E_1 \cap E_2)\). Thus, plugging into what we found before we get \[P(E_1 \cup E_2) = P(E_1) + P(E_2') = P(E_1) + P(E_2) - P(E_1 \cap E_2).\]

4. This follows exactly from the argument for (3). To see, first consider \(E_2 \cup E_3\) to be an event itself, say \(E_4\). Then we can apply the above result to \(E_1 \cup E_4\). And then we need only repeat the process for the remaining terms.

5. We can rewrite \(E_2\) as \(E_1 \cup (E_2 \cap E_1^C)\). These two sets are disjoint, since the one is \(E_1\) and the other must contain only elements in \(E_1^C\). Then, \(P(E_2) = P(E_1) + P(E_2 \cap E_1^C)\) by additivity. Then, through the non-negative property we know that \(P(E_2 \cap E_1^C) \geq 0\), and so rearranging we have \(P(E_1) = P(E_2) - P(E_2\cap E_1^C) \leq P(E_2)\).

These properties are useful when computing probabilities. In fact, these secondary properties will be used with more frequency than the basic axioms when manipulating probabilities in practice. It is worth building comfort with these properties, early and often, as they will assist in manipulating all probability expressions in the future.

While these properties hold in general for all probability models, it is instructive to focus on the equal probability model to begin building familiarity with probability. These properties allow us to take events – whether compound or simple – and combine, rewrite, and manipulate expressions to assist in the handling of the computations. Consider a simple event, \(A\).

Recall that a simple event is defined as single outcome of an experiment, and so in this case, \(A\) corresponds directly to an event that may be observed. If our sample space is \(k\) elements large, then \(P(A) = \dfrac{1}{k}\) in this framework. For instance, if \(A\) is the event that a two is rolled on a six-sided fair die, then \(P(A) = \dfrac{1}{6}\).

Now, suppose that a compound event is defined, \(B\). By definition, a compound event can be expressed as a set of possible outcomes from the experiment. Suppose that we enumerate these possible events as \(b_1, b_2, \dots, b_\ell\). Then we know that \(B\) occurs if any of \(b_1,b_2,\dots,b_\ell\) occur. Each \(b_j\) are elements of the sample space and correspond to possible outcomes of the experiment. As a result, we know that \(P(b_j) = \dfrac{1}{k}\), based on the equal probability assumption. Now, if we take any two distinct events, say \(b_i\) and \(b_j\), we know that they must be disjoint: \(b_i \cap b_j = \emptyset\). This is because in an experiment run only one outcome can occur. Moreover, we can say that \(B = b_1 \cup b_2 \cup\cdots\cup b_\ell\).Using the axioms of probability outlined above we therefore know that \(P(B) = \sum_{j=1}^\ell P(b_j) = \sum_{j=1}^\ell \dfrac{1}{k} = \dfrac{\ell}{k}\). This holds in general for any compound event in this setting.

If we take \(B\) to be the event that an even number is rolled on a six-sided die, then we would have \(b_1\) is the event that a two is rolled, \(b_2\) is the event that a four is rolled, and \(b_3\) is the event that a six is rolled. There are three such events, and so the probability that an even number is rolled must be \(\dfrac{3}{6} = 0.5\), which matches our intuition.

At its core, this process is counting up the number of ways that \(B\) can occur, and dividing by the total number of elements in the set. There were \(\ell\) ways of \(B\) occurring, and a total of \(k\) outcomes in the experiment, so the probability becomes \(\dfrac{\ell}{k}\). In the equal probability model, this will always be the case. The probability of any event \(A\) occurring is given by \[P(A) = \dfrac{N_A}{k},\] where \(N_A\) is the number of unique ways that \(A\) can occur. In other words, \(N_A\) is the size of the set \(A\), \(|A|\).

As a result of this, computing probabilities largely relies on the counting of possible outcomes corresponding to different events. If we can determine \(N_A = |A|\), and the count of the total number of occurrences, \(k\), then we can determine the probability of \(A\). This study of counting is known as combinatorics, and it is where we will turn our attention next.

Example 3.3 (Unmatched Six-Sided Dice) Charles and Sadie, not all together content with the progress through decks of cards, are considering games with dice. Suppose that they have two, fair, six-sided dice. They are interested in the probability that the two dice show different numbers when they are rolled. What is this probability?

Solution

We can solve this problem directly by counting up the number of ways that the two dice can show different numbers, and divide that by the total number of combinations. Consider the following enumeration of the possible realizations:

• 1, 1
• 1, 2
• 1, 3
• 1, 4
• 1, 5
• 1, 6

• 2, 1
• 2, 2
• 2, 3
• 2, 4
• 2, 5
• 2, 6

• 3, 1
• 3, 2
• 3, 3
• 3, 4
• 3, 5
• 3, 6

• 4, 1
• 4, 2
• 4, 3
• 4, 4
• 4, 5
• 4, 6

• 5, 1
• 5, 2
• 5, 3
• 5, 4
• 5, 5
• 5, 6

• 6, 1
• 6, 2
• 6, 3
• 6, 4
• 6, 5
• 6, 6

There are \(36\) possible outcomes. In each column, \(5\) of the options show different numbers, so that leads to a total of \(30\) outcomes showing different numbers, leading to a probability of \(\dfrac{30}{36} = \dfrac{5}{6}\).

Here, a faster way to approach the problem is to realize that the probability is easier to solve when considering the complement rather than the event itself. Notably, rolling two, fair, six-sided dice gives a total of \(36\) possible outcomes. Of these, exactly \(6\) have equal numbers showing on both dice. Thus, the probability that the two dice show the same number is going to be \(\dfrac{6}{36} = \dfrac{1}{6}\). Then, using the fact that \(P(E) = 1 - P(E^C)\), and that taking \(E\) to refer to the event where the two dice show different numbers, then \(E^C\) refers to the event that the two dice show the same number. As a result, the probability that we want is \(P(E) = 1 - \dfrac{1}{6} = \dfrac{5}{6}\).

Example 3.4 (Unmatched Arbitrary Dice) Charles and Sadie, working from their intrigue about dice, have decided that instead of using two six-sided dice, they wish to take two dice of possibly different sizes. Suppose that the first die has \(d_1\) sides and the second has \(d_2\) sides, and that both dice are otherwise fair. They are interested in the probability that the two dice show different numbers when they are rolled. What is this probability?

Solution

This problem is conceptually no different from Example 3.3. There will be a total of \(d_1\times d_2\) possible combinations of the two dice to be rolled.¹¹ Of these, the dice will match in \(\min\{d_1, d_2\}\) events.¹² Then, with the same complement trick, we get \[P(E) = 1 - P(E^C) = 1 - \frac{\min\{d_1,d_2\}}{d_1\times d_2}.\]

3.4 Combinatorics

3.4.1 The Product Rule

Fundamentally, counting is a matter of assessing the size of a collection of items. Sometimes, this is very straightforward. If you want to count the number of students in a classroom, you start at \(1\) and enumerate upwards through the integers. To count the number of days until the next Holiday, you do the same thing. If you really need to sleep, perhaps you will count imaginary sleep until you drift off. There is not much to this type of counting, and it is certainly deeply familiar to you all. However, it is also quite limited in its utility.

Imagine that you are interested in determining how many possible ways there are of arranging a deck of \(52\) cards. You could of course arrange them in a particular order, then count each of those. That would take a tremendous amount of time, so perhaps instead of using an actual deck you just write down the combinations. Still, each combination is going to be \(52\) cards long, and keeping track of that all will be a challenge. This seems like an approachable question, and yet, it illustrates how complicated (and large) these types of “counting” problems can become very quickly.

Fortunately for us there are some strategies for simplifying these problems down, some of which you are likely already familiar with. Think about trying to form an outfit where you have \(4\) different sweaters, \(3\) pairs of pants, and \(2\) options for your shoes. Suppose that any combination of these will work well. How many total outfits are there? Well, if you have already picked your sweater and pants, then there are going to be \(2\) different outfits using these: one with each of the pairs of shoes. This is true for each possible sweater-pant combination, and so we can count \(2\) for each one these. In other words, to get the total number of outfits we multiply the number of sweater-pant combinations by the number of shoe options. The same rationale can be applied to count the total number of sweater-pant combinations. For each sweater, there are \(3\) pairs of possible pants, and so to get the total number we can take \(3\) for each possible sweater, or in other words, \(3\times 4\). Taken together then we have \(4\times 3\times 2 = 24\) total possible outfits.

Another way of framing this is that we have to make three sequential decisions: which of the \(4\) sweaters, which of the \(3\) pants, and which of the \(2\) shoes are to be worn? When we do this we multiply through the number of alternatives at each decision point to get the total number of combinations. This is known as the product rule for counting.

Definition 3.1 (Product Rule for Counting) The product rule for counting states that, when there are a sequence of \(k\) decisions to be made, and for each decision \(j=1,\dots,k\), there are \(n_j\) options, then the total number of combinations will be \[N = n_1\times n_2\times\cdots\times n_k.\]

Example 3.5 (Counting Coffee Orders) When Charles and Sadie are out for coffee, Sadie enjoys ordering the same thing each time: a black coffee and vegan chocolate chip cookie. Charles, on the other hand, has decided to work through the entire menu of the local coffee shop, each day ordering a drink, with one add-in, and a snack. If there are \(10\) different drinks, \(8\) possible add-ins, and \(12\) different snacks, how many trips to the coffee shop will it take until Charles has tried it all?

Solution

This necessitates an application of the product rule for counting. Specifically, we can view this as three sequential decisions, where the first decision is which drink (with \(n_1 = 10\)), the second decision is which add-in (with \(n_2 = 8\)), and the third decision is which snack (with \(n_3 = 12\)). Taking the product gives the total number of combinations as \(10\times 8\times 12 = 960\). As a result, it will take \(960\) visits (assuming that nothing on the menu changes!) to try all combinations.

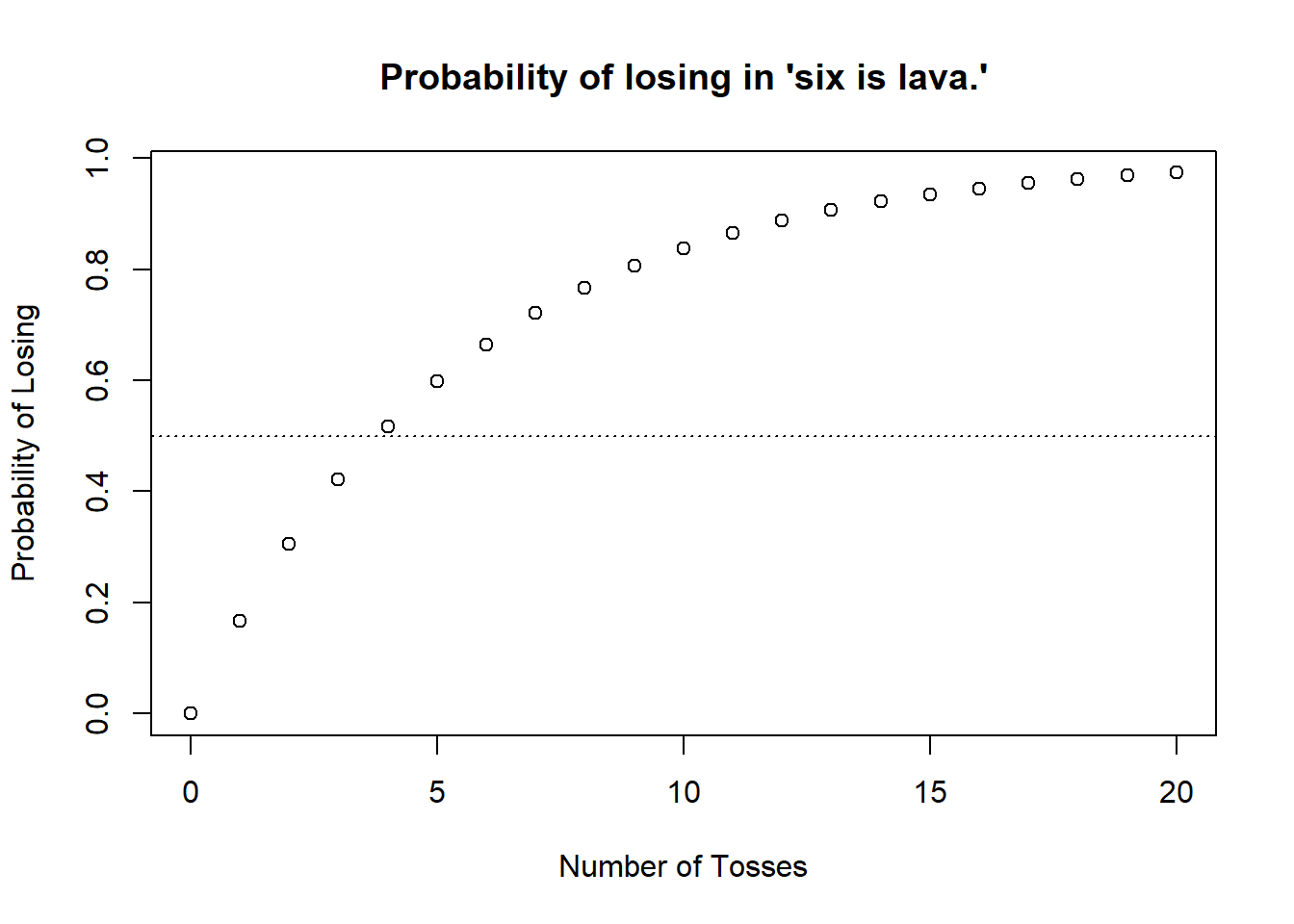
Example 3.6 (Sequence of Dice Rolls) Charles and Sadie have been enjoying playing with dice, but they lost one of the two they had. As a result, they are trying to come up with games revolving around rolling a single die. They decide to try a game called “six is lava”, where they roll a single six-sided die \(10\) times in a row. If they get \(1\) or more sixes, they lose the game. They are not sure if \(10\) is the correct number of rolls to use. What is the probability that they lose on any given set of \(10\) rolls of the die in this game?

Solution

Once again this is a scenario where using the complement simplifies the problem. If we asked “what is the probability that no 6’s are rolled, on \(10\) rolls of the die” then we can count the number of possibilities through an application of the product rule. In particular, there are going to be \(5\) options which are not \(6\) at each possible step. We can view this as have \(n_1 = n_2 = \cdots = n_{10} = 5\). Thus, the total number of ways of rolling no sixes is \(5\times5\times5\times\cdots\times5 = 5^{10}\).

Essentially the same process can be used to count the total number of possible rolls, replacing \(5\) with \(6\) to get the denominator. This means that there are \(6^{10}\) total sequences of \(10\) rolls, and \(5^{10}\) which contain no sixes. As a result, taking \(E\) to represent the probability that we observe no sixes on \(10\) rolls of the die, we would get \[P(E) = \frac{5^{10}}{6^{10}}.\] The question asks for \(E^C\) and so we take \[P(E^C) = 1 - P(E) = 1 - \left(\frac{5}{6}\right)^{10}.\] This is approximately 0.8385.

Note that if instead of \(10\) flips they had \(n\) flips, the probability would be \(1 - \left(5/6\right)^n\). We can plot this over various values of \(n\), to see how the number of flips impacts this probability. The probability of \(0.5\) is marked and we can see that taking \(4\) tosses gives an ever so slightly greater than \(0.5\) probability of losing (0.5177).

3.4.2 Tree Diagrams

Sometimes it is helpful to express counting rules graphically. To do so we rely on tree diagrams.

Definition 3.2 (Tree Diagram) A tree diagram is a graphical representation for the product rule for counting. Specifically, a tree diagram puts each of the decisions in sequence, and draws a branch for each separate option, starting from the branches drawn at the previous decision step.

To draw a tree diagram, you start with the first choice, drawing one branch for each of the \(n_1\) alternatives, labelling each. Then, at the second choice, you do the same process at the end of each of the branches you drew for choice \(1\), this time drawing \(n_2\) branches there (so you will have just drawn \(n_1\times n_2\) branches). Then for each of those you draw the \(n_3\) further branches, and so on and so forth until the end.

If you want to know the total number of choices, you count the end points at the very end of the diagram. Each branch corresponds to a single option. To determine which combination of choices it corresponds to, you read off the branch labels at each branch you take. If you want to know how many possible combinations come with certain options selected, you can look at only those branches which are downstream from the choices that you care about.

Figure 3.1: A generic tree diagram. Here the first choice has three different options and the second choice has two. We can see the six total combinations, labelled on the right of the diagram, and can trace the choices required to get there.

While tree diagrams can be quite useful for visualizing a problem, they often grow to be overly complex. As a result, we need to fall back on the numerical representation afforded to us through the product rule for counting. Counting problems, in general, can very quickly become large and complex. For this reason, we have several tools to assist us in reducing this complexity based on common types of problems that we would like to count.

3.4.3 The Factorial

The first useful tool for simplifying these problems is the factorial. The factorial of an integer, denoted by \(x!\) is given by the product of all integers from \(x\) to \(1\).¹³ That is, \[x! = x(x-1)(x-2)\cdots(2)(1).\] If we consider the product rule for counting then note that if \(n_1=1\), \(n_2=2\), … , \(n_k = k\), then the total number of options is \(k\times(k-1)\times\cdots\times 1 = k!\). The most common reason that this comes up is when we want to order a collection of items.

Suppose that you have \(10\) books that you want to place on a shelf. You can view this as making \(10\) sequential decisions: what book goes first, second, third, and so on. There are \(10\) options for the first book, then \(9\) for the second (any except for the first one), \(8\) for the third (any except for the first \(2\)). This continues down to the last book, and so we conclude that there are \(10\times9\times8\times\cdots\times1 = 10!\) ways of arranging these books.

Example 3.7 (Seating in a (Full) Coffee Shop) One day Charles and Sadie walk into the coffee shop and find that it is completely full. There are ten seats and ten people sitting in them. They are disappointed that they do not have room to sit themselves, however, they are never ones to pass up an interesting probability question.

1. How many different ways could these ten people have sat in these ten seats?
2. If there are ten drinks that have been made, and one is to be passed out to each seat, how many different ways can these ten people sit in these ten seats, with each of these ten drinks?
3. Alongside the ten drinks, there are ten snacks to be served up as well. How many different ways can these ten people sit in these ten seats, with each of these ten drinks, and each of these ten snacks?

Solution

1. Here, we can think about lining up the ten seats in a row, each number \(1\) through \(10\). Then, we want to place one patron into each of the seats. This is no different from ordering \(10\) books, and so the total is \(10!\) which is \(3,628,800\).

2. Note that we still have to make the seat choices from part (a), so there are \(10!\) ways of getting the \(10\) people sat in the \(10\) chairs. Once there, we can think of handing out the drinks to each of the numbered combinations of person-chair. This is no different from passing out the people as well, giving \(10!\) ways of doing this. We use the product rule to combine these two choices, with \(10!\times 10!\) total combinations of people-chair-drink. This is \(13,168,189,440,000\).

3. Extending the same logic before, there are \(10!\times 10!\) ways of getting each person sat in a chair with a drink. Then, there will be an additional \(10!\) ways of passing out the snacks to these people. Taken together this gives \(10!\times 10!\times 10!\) which is \(47,784,725,839,872,000,000\).¹⁴

Remark (0!). Depending on how factorials are thought of, some trouble can come up around a quantity like \(0!\). On one hand, if we view factorials as multiplying each number between \(n\) and \(1\) together then \(0! = 0\times 1\) and we get \(0! = 0\). On the other hand, if we view factorials as counting the number of ways which we can order a set of \(n\) items, then \(0!\) is the number of ways we can order \(0\) items, which is \(1\).¹⁵ So, which is it?

We take \(0!\) to be equal to \(1\). The ordering argument is perhaps the most convincing. However, if you are algebraically minded you may wonder how we get around the tricky issue of using our algebraic definition. The key insight is to not define \(n!\) as the product of the numbers from \(n\) to \(1\), but rather, to define \[(n-1)! = \frac{n!}{n},\] and specify that \(1! = 1\). Then in this case we get all of the usual requirements for how we have discussed factorials, but we also get that \(0! = \dfrac{(0+1)!}{(0+1)} = 1\). As a result, we will take \(0! = 1\).¹⁶

3.4.4 Permutations and Combinations

Sometimes, we want to order items from a collection, but we want to only take a subset of these items. That is, suppose that you have \(20\) books, only \(9\) of them will fit on the shelf, and you want to know “how many ways can you put \(9\) books on the shelf, in order, from your collection of \(20\)?” Using the product rule of counting for this directly, we recognize that there are \(20\) options for the first, then \(19\), then \(18\), and so on until there are \(12\) choices for the \(9\)th book to place. We can write this out in a seemingly strange way. \[\begin{align*} &\ (20)(19)(18)(17)(16)(15)(14)(13)(12) \\ &= \frac{(20)(19)(18)(17)(16)(15)(14)(13)(12)(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1)}{(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1)} \\ &= \frac{(20)(19)(18)(17)(16)(15)(14)(13)(12)\cancel{(11)}\cancel{(10)}\cancel{(9)}\cancel{(8)}\cancel{(7)}\cancel{(6)}\cancel{(5)}\cancel{(4)}\cancel{(3)}\cancel{(2)}\cancel{(1)}}{\cancel{(11)}\cancel{(10)}\cancel{(9)}\cancel{(8)}\cancel{(7)}\cancel{(6)}\cancel{(5)}\cancel{(4)}\cancel{(3)}\cancel{(2)}\cancel{(1)}} \end{align*}\]

This expression is \(20!\) divided by \(11!\), and gives the same as our argument from the product rule for counting directly. This is a more general result than our example with books would suggest. If we have \(n\) items, and we want to choose \(k\) of them taking into account the order those choices, it will always be \(n!\) divided by \((n-k)!\). We call this a permutation.

Definition 3.3 (Permutations) If we wish to select \(k\) items from a collection of \(n\) items, where the ordering of these selections matters, then the total number is referred to as a permutation. Mathematically, \[P_{n,k} = \frac{n!}{(n-k)!}.\]

Permutations arise when we select ordered subsets from a collection. We often, in combinatorial problems, talk about ordering, though sometimes what we mean by this is slightly more abstract. Suppose that you want to form a committee with \(5\) different people, each of which occupies a different role: the president, vice president, treasurer, note taker, and critic. If there are \(30\) people to select for this then there are \(P_{30,5}\) total possible committees that can be formed. While there is not a sequential order here, we talk about this as being “ordered” since we can differentiate between the five roles. Instead of labelling them with their names, we could label them \(1\) through \(5\) and make the ordering more explicit.

Example 3.8 (Seating in a (Not Full) Coffee Shop) Still haunted by that time when the coffee shop was full, Sadie and Charles enter the coffee shop at a later date and find that, including themselves, there are only \(7\) patrons in the store, and still the \(10\) seats to choose from.

1. How many different ways can the \(7\) people sit in the \(10\) different chairs?
2. If there are \(10\) drinks on the menu, how many different ways can each person choose a chair and a drink?
3. If the coffee shop can make only one of each drink, how does the previous total change?

Solution

1. In this case we are looking to order subsets from a total collection. If we line up the \(7\) patrons we then need to select \(7\) chairs to go with them, and keep these ordered. This is \[P_{10,7} = \frac{10!}{3!} = 604800.\]

2. In this part of the question we know that the \(7\) people have \(P_{10,7}\) ways of sitting into seats, we can view this as decision one. Then, for each of these \(7\) people there is a decision of what drink they will order. For these \(7\) decisions, \(n_2 = \cdots = n_8 = 10\). As a result, we get the total number is \[P_{10,7}\times10\times10\times\cdots\times10 = P_{10,7}\times 10^{7} = 6,048,000,000,000.\]

3. This setting, like part (b) starts with a first decision involving \(P_{10,7}\) choices. Then, instead of there being \(7\) more decisions with \(10\) choices each, we can either view this as \(7\) more choices with a descending number of options \(10\) for the first, then \(9\), and so on, or we can view this as a single choice where we need to select \(7\) ordered options from the \(10\) drinks available. This gives \[P_{10,7} \times P_{10,7} = 365,783,040,000,\] total choices.

Factorials compute the number of orderings for a set of objects, and permutations compute the number of ordered subsets from a collection of objects. What about when we do not wish to differentiate the order of subsets? Suppose that you still need to form a \(5\) person committee, but you do not have explicit roles for the different members of the committee. Here we cannot use a permutation directly, as we know that this takes into account the order.

To determine the number of unordered subsets, we will consider an alternative approach that we could have used for taking ordered subsets. Suppose that we formulate the ordered committee as a two step procedure. First, we select \(5\) people without concern for their order. Then we choose which order they will have. If \(M\) represents the number of unordered sets of \(5\) from this population, the product rule for counting tells us that the total number of ordered committees will be \(M\times 5!\), since there are \(5!\) arrangements of the \(5\) people. Thus, we can write this down as \[P_{30,5} = \frac{30!}{25!} = M\times 5! \implies M = \frac{30!}{25!5!}.\]

This will be true in general. If we want to select \(k\) items from a collection of \(n\), we will have \(n!\) divided by the product of \(k!\) and \((n-k)!\). We refer to these as combinations.

Definition 3.4 (Combinations) If we wish to select \(k\) items from a collection of \(n\) items, where the ordering of these selections does not matter, then the total number is referred to as a combination. Mathematically, \[\binom{n}{k} = \frac{n!}{k!(n-k)!}.\]

We read \(\dbinom{n}{k}\) as “\(n\) choose \(k\)”, which translates to “select \(k\) items from a population of \(n\) total options, without concern for their order.”

To summarize: factorials allow us to order a complete collection, permutations allow us to select a subset with consideration of the ordering, and combinations allow us to select a subset from the collection without regard to the order. These three techniques can be used in combination with the product rule for counting to allow us to have very complex total summations.

Example 3.9 (Changing the Seating in the Coffee Shop) Some nights, the coffee shop hosts local music acts. Because of the added equipment, the coffee shop owners only keep out the number of seats that are going to be required based on the number of tickets that were sold.

1. If there are \(8\) tickets sold, how many different combinations of the \(10\) chairs can get left out?
2. Suppose that only \(6\) people end up showing up. How many different ways can the \(6\) people sit in the \(8\) chairs that are being selected from the \(10\) total possibilities?

Solution

1. Here, there is no ordering for the \(8\) chairs that are to be selected. As a result, we are looking for how many chairs can be selected from a group of \(10\) of them. This is \[\binom{10}{8} = \frac{10!}{8!\cdot 2!} = 45.\]

2. With the first choice having \(45\) possible options, the second choice that needs to be made is how \(6\) people sit into \(8\) chairs. Here the ordering does matter, since the chairs are distinguishable. As a result, this is a permutations question, with there being a total of \(P_{8,6} = \frac{8!}{2!}\) ways of having the people select their seats. In total then there are \[\binom{10}{8}\times P_{8,6} = \frac{10!}{8!\cdot 2!}\cdot\frac{8!}{2!} = 907,200.\]

Example 3.10 (Fundraiser Raffle Consultation) Charles and Sadie are asked by a local organization to help organize a raffle as a fundraiser. The organizers are considering two different versions for the raffle.

1. They would sell \(1000\) tickets, and there are \(5\) different prizes (valued at $1000, $500, $250, $150, and $100) respectively.
2. They would sell \(1000\) tickets, and draw \(5\) winners. Each winner would win $400.

They are curious how these two scenarios differ statistically.

1. How many possible winning combinations exist for scenario 1?
2. How many possible winning combinations exist for scenario 2?
3. Are the probabilities that any specific individual wins the raffle different between the two versions? Explain.

Solution

1. In the first scenario, the ordering of the winners matters. We can think of drawing the \(5\) winners in order from highest value prize to lowest value prize. Then, we are selecting \(k=5\) from \(n=1000\) with concern for ordering, so the total number of winning combinations is \[P_{1000,5} = \frac{1000!}{995!} = 990,034,950,024,000.\]

2. In the second scenario, the ordering of the winners does not matter. There is no distinction between the winners, and so we could select any \(5\) and then report the winners alphabetically. Then, we are selecting \(k=5\) from \(n=1000\) with no concern for ordering, so the total number of winning combinations is \[\binom{1000}{5} = \frac{1000!}{5!995!} = 8,250,291,250,200.\]

3. Intuitively, the probabilities should be the same. Moreover, it makes sense that each probability should be \(5/1000\) since the probability of winning any of the prizes is \(1/1000\) and there are \(5\) such prizes to win.

   In parts (a) and (b) we saw the total number of each version, and we know that any sequence of winners is equally likely. As a result, we can consider counting the total number of ways that any specific individual can win in both scenarios. In the first, suppose that the individual wins the top prize. Then we need to select 4 other winners (with ordering) from the remaining \(999\) individuals. Thus, the total number of ways that they can win the $1000 prize is \(P_{999,4}\). The same goes for all of the other prizes, meaning the total number of ways that they can win is \(5\times P_{999,4}\). Thus, the probability that they win is \[\frac{5P_{999,4}}{P_{1000,5}} = \frac{5(999!/995!)}{1000!/995!} = \frac{5}{1000}.\]

   For the second option, if we know that the particular individual wins then we need to select the other \(4\) winners from the remaining \(999\) individuals, without concern for the ordering. Thus, there are \(\dbinom{999}{4}\) winning combinations for the specific individual, and the probability that they win is \[\frac{\binom{999}{4}}{\binom{1000}{5}} = \frac{999! \times 5! \times 995!}{995!\times 4! \times 1000!} = \frac{5}{1000}.\]

3.4.5 Less Common Counting Techniques

While most of the problems we address will revolve around permutations and combinations (with heavy use of the product rule), there are additional techniques which are important to know (and recognize when to use). In particular, combinations and permutations each assume that we are sampling from our set without replacement. That is, each time you select an item, it is removed from the population. These are the most common situations in these combinatorial problems, however, there are some situations which arise where we need to count the number of ordered or unordered subsets with replacement.

3.4.5.1 Ordered Subsets with Replacement

Consider, for instance, forming a password using only lowercase numbers and letters. If you decide on a fixed length for the password, then there are going to be \(36\) choices at each decision point, and you want to take an ordered subset of these. This is forming an ordered subset with replacement, and to count how many different ways there are of doing this, we can use the product rule. That is, you have \(36\) choices at each decision point, and so there are \(36\times 36\times\cdots\times 36 = 36^k\) total decisions, where \(k\) is the number of items to select.

In general, if you have \(n\) total items and you want to make an ordered set of \(k\) of these items with replacement you will have \(n^k\) total ways of doing this.

3.4.5.2 Unordered Subsets with Replacement

Forming unordered sets with replacement is slightly less intuitive. Consider rolling \(k\) dice which are not distinguishable from one another. We know that there are \(6\) total sides that can show up on each of these dice, but how many different combinations of numbers can show up overall? If the dice can be distinguished we would say that there are \(6^k\) possible ways of doing this. However, some of these combinations are going to be equivalent in the unordered world. Take the simple case of \(k=2\). Here we have the following possibilities: \[\begin{align*} (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)&\\ (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)&\\ (3, 3), (3, 4), (3, 5), (3, 6)&\\ (4, 4), (4, 5), (4, 6)&\\ (5, 5), (5, 6)&\\ (6,6)& \end{align*}\]

This gives a total of \(21\) possible combinations, rather than \(36\).

In general, if we want to find the way of selecting \(k\) elements with replacement from a total of \(n\), then the number of ways of doing this will be \[\binom{n+k-1}{k}.\] In our example this gives \(\binom{6+2-1}{2} = 21\).

3.4.5.3 Permutations with Identical Objects

Finally, it is worth understanding how to handle identical objects in combinatorial problems. Suppose that, of the \(10\) books that we wish to place on a shelf, we have \(2\) copies of one of them, \(3\) copies of another one, and the other \(5\) have one copy each. Supposing that there is no way to tell these identical objects apart, how many ways can we arrange the bookshelf?

First, if we pretend that all of the items are actually able to be differentiated then there are \(10!\) ways of placing these books. Now, in any of these permutations, had we swapped the order of the first book (with \(2\) copies) the ordering would have been indistinguishable. As a result, for every ordering of the \(8\) other books, we counted that permutation twice (when it should have only been counted once!). So to address the two repeated copies we need to take \(10!/2\). Now, a similar argument is going to hold for the book with \(3\) repeated copies. However, instead of there being \(2\) permutations which are identical, there are going to be \(3! = 6\) permutations which are identical. This is because we can reorder the \(3\) copies of the book in anyway we choose, and still wind up with the same overall permutation.¹⁷ As a result, the total number is going to be \[\frac{10!}{2!\cdot3!} = 302400.\]

We can see this same result through an alternative construction. First, we select which of the \(10\) slots should have the first book. We do not care about the order, and so there are \(\binom{10}{2}\) ways of doing this. Next, we can select which of the \(8\) remaining slots should have the second book. Like the first one there will be \(\binom{8}{3}\) ways of placing these. Now, there are \(5\) slots remaining, and \(5\) books to place, so as a result, we can order those in \(5!\) different ways, and then slot them into the remaining places in order. This gives, in total \[\binom{10}{2}\binom{8}{3}(5!) = \frac{10!}{2!\cancel{8!}}\cdot\frac{\cancel{8!}}{3!\cancel{5!}}\cdot\cancel{5!} = \frac{10!}{2!3!}.\]

To generalize this, if we want to order \(n\) elements, such that there are \(k\) distinguishable elements with \(n_1\) of the first type, \(n_2\) of the second, and so forth until \(n_k\) of the last type (\(n = n_1 + n_2 + \cdots + n_k\)), then the total number of orderings will be \[\frac{n!}{n_1!\cdot n_2!\cdots n_k!}.\]

3.5 From Combinatorics to Probability

While combinatorics is a field of study on its own, with many intriguing tools and developments surrounding the enumeration of objects, for the purposes of simple probability models these tools will suffice. Ultimately, we care about counting since in the equal probability model, the probability of any event can be determined by counting the number of ways that the event can occur and dividing by the total number of outcomes that are possible. That is, we use these tools to derive \(N_A\), the total number of ways that \(A\) can occur, and \(N\), the total number of experimental outcomes, and then we conclude that \[P(A) = \frac{N_A}{N}.\]

Example 3.11 (Poker Hand Counts) During one of their conversations, Charles and Sadie were remarking how they never really played poker. As they understand it, in poker you are dealt a hand of \(5\) cards and you want to use these \(5\) cards to try to match certain sets of cards, some of which are more rare than others. Charles and Sadie start to get hung-up on discussions regarding “straights” and “flushes”.

A straight is any sequence of \(5\) cards in ascending order (where aces can be low, or high). For instance, \(7, 8, 9, 10, \text{J}\) of any suit. A flush, is any set of \(5\) cards belonging to the same suit. Charles just feels that straights have to be more rare than flushes.

1. How many different straights are there from a standard deck of cards?
2. How many different flushes are there from a standard deck of cards?
3. If dealt \(5\) cards at random, what is the probability of a flush? What is the probability of a straight?
4. A straight flush occurs when you have \(5\) cards in order, of the same suit. What is the probability of a straight flush?
5. If straight flushes were not counted as flushes, and not counted as straights, how do the probabilities of either hand change?

Solution

1. A straight necessitates drawing five cards in order, with each of any suit. Just as with the straight flush, there are \(10\) possible starting values for the straight. Once we have selected the starting value, then for each of the five cards we can pick any of the four suits, resulting in \(4\) choices each. That gives \[N_A = 10\times 4\times 4\times 4\times 4\times 4 = 10\times 4^5 = 10240.\]

2. A flush necessitates drawing any five cards from the same suit. If we had a suit fixed, there would be \({13\choose 5}\) ways of doing this, since we do not care about ordering. If we think about first choosing the suit, we have \(4\) ways of doing that, resulting in \[N_A = 4 \times {13 \choose 5} = 5148.\]

3. To find the probabilities of each of these, we need to know the total number of \(5\) card hands. We do not consider order, and so \(N = \binom{52}{5} = 2598960\). Then, the probability is the number of combinations (calculated above) divided by the number of hands. This gives, for straights, \[P(A) = \frac{10240}{2598960} = \frac{128}{32487} \approx 0.00394,\] and for flushes, \[P(A) = \frac{5148}{2598960} = \frac{33}{16660} \approx 0.00198.\] As a result, we see that straights are roughly twice as common as flushes are.¹⁸

4. Note that to form a straight flush, we first have to fix a suit. There are \({4\choose 1}=4\) total ways of doing this. Next, we need to pick which starting value we will use. Once a card has been selected as a starting value, the remaining cards are fixed. The start value ranges from A through to \(10\). Correspondingly, we have \[N_A = {4\choose 1}{10 \choose 1} = 4\times10 = 40.\] As a result, we get that \[P(A) = \frac{40}{2598960} = \frac{1}{64974}.\]

5. From (d) exactly \(40\) of the straights and \(40\) of the flushes are also straight flushes. We can thus remove \(40\) from the totals of each of these, giving \(\dfrac{10200}{2598960}\) for straights and \(\dfrac{5108}{2598960}\) for flushes.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 3.1

The probability that a smartphone does not break during the first year of use is \(0.504\). What is the probability that the smartphone breaks during the first year of use?

(Question ID: 0571506039)

The probability that a website does not load in under 3 seconds is \(0.936\). What is the probability that the website loads in under 3 seconds?

(Question ID: 0975464043)

The probability that a smartphone does not break during the first year of use is \(0.628\). What is the probability that the smartphone breaks during the first year of use?

(Question ID: 0547928482)

The probability that a customer is not satisfied with the service is \(0.276\). What is the probability that the customer is satisfied with the service?

(Question ID: 0559282069)

The probability that a project is completed by the deadline is \(0.265\). What is the probability that the project is not completed by the deadline?

(Question ID: 0938433505)

The probability that a car does not start on the first try is \(0.282\). What is the probability that the car starts on the first try?

(Question ID: 0075755065)

The probability that a plant grows taller this month is \(0.38\). What is the probability that the plant does not grow taller this month?

(Question ID: 0732314337)

The probability that a team wins the game is \(0.26\). What is the probability that the team does not win the game?

(Question ID: 0008624060)

The probability that a river freezes in winter is \(0.761\). What is the probability that the river does not freeze in winter?

(Question ID: 0839127655)

The probability that a student does not pass the exam is \(0.168\). What is the probability that the student passes the exam?

(Question ID: 0334275642)

The probability that a student passes the exam is \(0.522\). What is the probability that the student does not pass the exam?

(Question ID: 0656705088)

The probability that a student passes the exam is \(0.572\). What is the probability that the student does not pass the exam?

(Question ID: 0693060819)

The probability that a train arrives at the scheduled time is \(0.05\). What is the probability that the train does not arrive at the scheduled time?

(Question ID: 0030580179)

The probability that a student does not pass the exam is \(0.183\). What is the probability that the student passes the exam?

(Question ID: 0196435756)

The probability that it does not rain tomorrow is \(0.288\). What is the probability that it rains tomorrow?

(Question ID: 0834301016)

The probability that a river freezes in winter is \(0.897\). What is the probability that the river does not freeze in winter?

(Question ID: 0005899163)

The probability that it does not rain tomorrow is \(0.613\). What is the probability that it rains tomorrow?

(Question ID: 0309410486)

The probability that a flower blooms in spring is \(0.002\). What is the probability that the flower does not bloom in spring?

(Question ID: 0756353183)

The probability that a meeting does not start on time is \(0.081\). What is the probability that the meeting starts on time?

(Question ID: 0870483617)

The probability that a customer is not satisfied with the service is \(0.104\). What is the probability that the customer is satisfied with the service?

(Question ID: 0635666160)

The probability that a website loads in under 3 seconds is \(0.461\). What is the probability that the website does not load in under 3 seconds?

(Question ID: 0471878192)

The probability that a river does not freeze in winter is \(0.807\). What is the probability that the river freezes in winter?

(Question ID: 0722394021)

The probability that a student passes the exam is \(0.258\). What is the probability that the student does not pass the exam?

(Question ID: 0547385829)

The probability that a smartphone does not break during the first year of use is \(0.533\). What is the probability that the smartphone breaks during the first year of use?

(Question ID: 0773670214)

The probability that a customer is satisfied with the service is \(0.304\). What is the probability that the customer is not satisfied with the service?

(Question ID: 0418590889)

The probability that a plant grows taller this month is \(0.991\). What is the probability that the plant does not grow taller this month?

(Question ID: 0046200067)

The probability that a ticket wins a prize is \(0.964\). What is the probability that the ticket does not win a prize?

(Question ID: 0232227299)

The probability that a car starts on the first try is \(0.754\). What is the probability that the car does not start on the first try?

(Question ID: 0220971402)

The probability that a student does not pass the exam is \(0.903\). What is the probability that the student passes the exam?

(Question ID: 0760236750)

The probability that it does not rain tomorrow is \(0.847\). What is the probability that it rains tomorrow?

(Question ID: 0816018936)

The probability that it rains tomorrow is \(0.345\). What is the probability that it does not rain tomorrow?

(Question ID: 0614561612)

The probability that a particular package does not break during shipment is \(0.355\). What is the probability that the particular package breaks during shipment?

(Question ID: 0341750415)

The probability that it does not rain tomorrow is \(0.102\). What is the probability that it rains tomorrow?

(Question ID: 0337991307)

The probability that a customer is not satisfied with the service is \(0.512\). What is the probability that the customer is satisfied with the service?

(Question ID: 0390300895)

The probability that a customer is not satisfied with the service is \(0.391\). What is the probability that the customer is satisfied with the service?

(Question ID: 0551397844)

The probability that a river freezes in winter is \(0.142\). What is the probability that the river does not freeze in winter?

(Question ID: 0429829410)

The probability that a light bulb burns out this week is \(0.883\). What is the probability that the light bulb does not burn out this week?

(Question ID: 0050322632)

The probability that a plant does not grow taller this month is \(0.227\). What is the probability that the plant grows taller this month?

(Question ID: 0421247229)

The probability that a particular package breaks during shipment is \(0.184\). What is the probability that the particular package does not break during shipment?

(Question ID: 0193618460)

The probability that a team wins the game is \(0.899\). What is the probability that the team does not win the game?

(Question ID: 0078322062)

The probability that a plant does not grow taller this month is \(0.101\). What is the probability that the plant grows taller this month?

(Question ID: 0249056070)

The probability that a flower does not bloom in spring is \(0.443\). What is the probability that the flower blooms in spring?

(Question ID: 0038799228)

The probability that a customer is not satisfied with the service is \(0.678\). What is the probability that the customer is satisfied with the service?

(Question ID: 0246405683)

The probability that a particular package does not break during shipment is \(0.599\). What is the probability that the particular package breaks during shipment?

(Question ID: 0385207410)

The probability that a ticket wins a prize is \(0.57\). What is the probability that the ticket does not win a prize?

(Question ID: 0801248642)

The probability that a river does not freeze in winter is \(0.724\). What is the probability that the river freezes in winter?

(Question ID: 0490945215)

The probability that a ticket does not win a prize is \(0.667\). What is the probability that the ticket wins a prize?

(Question ID: 0295973439)

The probability that a project is not completed by the deadline is \(0.212\). What is the probability that the project is completed by the deadline?

(Question ID: 0996176265)

The probability that a flower blooms in spring is \(0.808\). What is the probability that the flower does not bloom in spring?

(Question ID: 0794159828)

The probability that a student passes the exam is \(0.543\). What is the probability that the student does not pass the exam?

(Question ID: 0344352069)

Self Assessment 3.2

A ball is drawn at random from a box containing \(49\) red balls, \(6\) white balls, and \(17\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0641807344)

A ball is drawn at random from a box containing \(8\) red balls, \(10\) white balls, and \(49\) blue balls. What is the probability that the ball is not white?

(Question ID: 0637116237)

A ball is drawn at random from a box containing \(15\) red balls, \(39\) white balls, and \(50\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0460606047)

A ball is drawn at random from a box containing \(29\) red balls, \(13\) white balls, and \(50\) blue balls. What is the probability that the ball is not red?

(Question ID: 0480824942)

A ball is drawn at random from a box containing \(38\) red balls, \(29\) white balls, and \(7\) blue balls. What is the probability that the ball is not red?

(Question ID: 0021971990)

A ball is drawn at random from a box containing \(32\) red balls, \(25\) white balls, and \(47\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0360817529)

A ball is drawn at random from a box containing \(26\) red balls, \(37\) white balls, and \(34\) blue balls. What is the probability that the ball is red?

(Question ID: 0146291302)

A ball is drawn at random from a box containing \(19\) red balls, \(20\) white balls, and \(11\) blue balls. What is the probability that the ball is not red?

(Question ID: 0947008059)

A ball is drawn at random from a box containing \(46\) red balls, \(7\) white balls, and \(34\) blue balls. What is the probability that the ball is blue?

(Question ID: 0223369187)

A ball is drawn at random from a box containing \(46\) red balls, \(21\) white balls, and \(10\) blue balls. What is the probability that the ball is red or white?

(Question ID: 0366079325)

A ball is drawn at random from a box containing \(25\) red balls, \(9\) white balls, and \(41\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0366617717)

A ball is drawn at random from a box containing \(21\) red balls, \(25\) white balls, and \(39\) blue balls. What is the probability that the ball is not white?

(Question ID: 0419703062)

A ball is drawn at random from a box containing \(40\) red balls, \(14\) white balls, and \(30\) blue balls. What is the probability that the ball is blue?

(Question ID: 0064938046)

A ball is drawn at random from a box containing \(20\) red balls, \(9\) white balls, and \(34\) blue balls. What is the probability that the ball is not white?

(Question ID: 0211916989)

A ball is drawn at random from a box containing \(43\) red balls, \(24\) white balls, and \(28\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0359705111)

A ball is drawn at random from a box containing \(45\) red balls, \(18\) white balls, and \(23\) blue balls. What is the probability that the ball is red or blue?

(Question ID: 0486028828)

A ball is drawn at random from a box containing \(20\) red balls, \(39\) white balls, and \(30\) blue balls. What is the probability that the ball is red?

(Question ID: 0478664134)

A ball is drawn at random from a box containing \(15\) red balls, \(11\) white balls, and \(17\) blue balls. What is the probability that the ball is blue?

(Question ID: 0350846517)

A ball is drawn at random from a box containing \(13\) red balls, \(38\) white balls, and \(18\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0045047766)

A ball is drawn at random from a box containing \(42\) red balls, \(11\) white balls, and \(43\) blue balls. What is the probability that the ball is blue?

(Question ID: 0186400177)

A ball is drawn at random from a box containing \(35\) red balls, \(25\) white balls, and \(33\) blue balls. What is the probability that the ball is not red?

(Question ID: 0817157071)

A ball is drawn at random from a box containing \(29\) red balls, \(14\) white balls, and \(47\) blue balls. What is the probability that the ball is blue?

(Question ID: 0574181227)

A ball is drawn at random from a box containing \(42\) red balls, \(12\) white balls, and \(23\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0223081713)

A ball is drawn at random from a box containing \(12\) red balls, \(11\) white balls, and \(23\) blue balls. What is the probability that the ball is not red?

(Question ID: 0626047292)

A ball is drawn at random from a box containing \(32\) red balls, \(39\) white balls, and \(17\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0996718093)

A ball is drawn at random from a box containing \(5\) red balls, \(29\) white balls, and \(27\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0168472448)

A ball is drawn at random from a box containing \(18\) red balls, \(21\) white balls, and \(22\) blue balls. What is the probability that the ball is not white?

(Question ID: 0551262246)

A ball is drawn at random from a box containing \(42\) red balls, \(40\) white balls, and \(45\) blue balls. What is the probability that the ball is not white?

(Question ID: 0059932786)

A ball is drawn at random from a box containing \(27\) red balls, \(34\) white balls, and \(15\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0270748397)

A ball is drawn at random from a box containing \(25\) red balls, \(29\) white balls, and \(28\) blue balls. What is the probability that the ball is red?

(Question ID: 0759704301)

A ball is drawn at random from a box containing \(32\) red balls, \(22\) white balls, and \(48\) blue balls. What is the probability that the ball is red or white?

(Question ID: 0016541622)

A ball is drawn at random from a box containing \(26\) red balls, \(12\) white balls, and \(30\) blue balls. What is the probability that the ball is blue?

(Question ID: 0578801723)

A ball is drawn at random from a box containing \(32\) red balls, \(40\) white balls, and \(33\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0182305286)

A ball is drawn at random from a box containing \(50\) red balls, \(9\) white balls, and \(20\) blue balls. What is the probability that the ball is red?

(Question ID: 0062161172)

A ball is drawn at random from a box containing \(19\) red balls, \(8\) white balls, and \(23\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0462598950)

A ball is drawn at random from a box containing \(39\) red balls, \(22\) white balls, and \(46\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0942255388)

A ball is drawn at random from a box containing \(16\) red balls, \(20\) white balls, and \(17\) blue balls. What is the probability that the ball is red or white?

(Question ID: 0764489836)

A ball is drawn at random from a box containing \(33\) red balls, \(40\) white balls, and \(31\) blue balls. What is the probability that the ball is red or white?

(Question ID: 0299464345)

A ball is drawn at random from a box containing \(21\) red balls, \(26\) white balls, and \(31\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0750258392)

A ball is drawn at random from a box containing \(23\) red balls, \(10\) white balls, and \(17\) blue balls. What is the probability that the ball is not blue?

(Question ID: 0328762688)

A ball is drawn at random from a box containing \(28\) red balls, \(37\) white balls, and \(15\) blue balls. What is the probability that the ball is blue?

(Question ID: 0215081818)

A ball is drawn at random from a box containing \(26\) red balls, \(34\) white balls, and \(32\) blue balls. What is the probability that the ball is white or blue?

(Question ID: 0441143437)

A ball is drawn at random from a box containing \(31\) red balls, \(18\) white balls, and \(39\) blue balls. What is the probability that the ball is red?

(Question ID: 0033288154)

A ball is drawn at random from a box containing \(10\) red balls, \(29\) white balls, and \(6\) blue balls. What is the probability that the ball is white?

(Question ID: 0023282731)

A ball is drawn at random from a box containing \(32\) red balls, \(38\) white balls, and \(50\) blue balls. What is the probability that the ball is not white?

(Question ID: 0995122549)

A ball is drawn at random from a box containing \(7\) red balls, \(28\) white balls, and \(8\) blue balls. What is the probability that the ball is red or blue?

(Question ID: 0224225247)

A ball is drawn at random from a box containing \(10\) red balls, \(50\) white balls, and \(36\) blue balls. What is the probability that the ball is not white?

(Question ID: 0208003512)

A ball is drawn at random from a box containing \(10\) red balls, \(14\) white balls, and \(45\) blue balls. What is the probability that the ball is not red?

(Question ID: 0469975325)

A ball is drawn at random from a box containing \(33\) red balls, \(48\) white balls, and \(26\) blue balls. What is the probability that the ball is red?

(Question ID: 0629582727)

A ball is drawn at random from a box containing \(25\) red balls, \(12\) white balls, and \(17\) blue balls. What is the probability that the ball is red or white?

(Question ID: 0813007211)

Self Assessment 3.3

Let \(I\) be the event that a randomly selected university student has taken any course in international relations, and \(J\) be the event that a randomly selected university student has taken any course in journalism. Suppose that \(P(I) = 0.232\), \(P(J) = 0.158\), and \(P(I \cap J) = 0.131\). What is the probability that the student has taken either a course in either international relations or journalism?

(Question ID: 0247609104)

Let \(J\) be the event that a randomly selected university student has taken any course in journalism, and \(R\) be the event that a randomly selected university student has taken any course in religion. Suppose that \(P(J) = 0.497\), \(P(R) = 0.524\), and \(P(J \cap R) = 0.209\). What is the probability that the student has taken a course in journalism but not in religion?

(Question ID: 0095449880)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(K\) be the event that a randomly selected university student has taken any course in kinesiology. Suppose that \(P(Q) = 0.264\), \(P(K) = 0.23\), and \(P(Q \cap K) = 0.059\). What is the probability that the student has not taken a course in either of quantum mechanics or kinesiology?

(Question ID: 0225600262)

Let \(G\) be the event that a randomly selected university student has taken any course in geography, and \(T\) be the event that a randomly selected university student has taken any course in theater. Suppose that \(P(G) = 0.689\), \(P(T) = 0.439\), and \(P(G \cup T) = 0.962\). What is the probability that the student has taken either a course in both geography and theater?

(Question ID: 0231678626)

Let \(F\) be the event that a randomly selected university student has taken any course in french, and \(R\) be the event that a randomly selected university student has taken any course in religion. Suppose that \(P(F) = 0.86\), \(P(R) = 0.181\), and \(P(F \cup R) = 0.952\). What is the probability that the student has taken a course in religion but not in french?

(Question ID: 0636879840)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(H\) be the event that a randomly selected university student has taken any course in history. Suppose that \(P(S) = 0.613\), \(P(H) = 0.229\), and \(P(S \cap H) = 0.192\). What is the probability that the student has taken a course in history but not in statistics?

(Question ID: 0192990386)

Let \(R\) be the event that a randomly selected university student has taken any course in religion, and \(V\) be the event that a randomly selected university student has taken any course in visual arts. Suppose that \(P(R) = 0.858\), \(P(V) = 0.253\), and \(P(R \cup V) = 0.99\). What is the probability that the student has taken a course in visual arts but not in religion?

(Question ID: 0849725410)

Let \(R\) be the event that a randomly selected university student has taken any course in religion, and \(S\) be the event that a randomly selected university student has taken any course in statistics. Suppose that \(P(R) = 0.125\), \(P(S) = 0.127\), and \(P(R \cap S) = 0.087\). What is the probability that the student has taken either a course in either religion or statistics?

(Question ID: 0638878645)

Let \(C\) be the event that a randomly selected university student has taken any course in chemistry, and \(D\) be the event that a randomly selected university student has taken any course in design. Suppose that \(P(C) = 0.424\), \(P(D) = 0.348\), and \(P(C \cap D) = 0.188\). What is the probability that the student has taken a course in design but not in chemistry?

(Question ID: 0650498398)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(P\) be the event that a randomly selected university student has taken any course in psychology. Suppose that \(P(S) = 0.453\), \(P(P) = 0.198\), and \(P(S \cup P) = 0.512\). What is the probability that the student has taken a course in psychology but not in statistics?

(Question ID: 0170669903)

Let \(A\) be the event that a randomly selected university student has taken any course in art history, and \(N\) be the event that a randomly selected university student has taken any course in neuroscience. Suppose that \(P(A) = 0.621\), \(P(N) = 0.333\), and \(P(A \cup N) = 0.826\). What is the probability that the student has taken a course in neuroscience but not in art history?

(Question ID: 0518092260)

Let \(L\) be the event that a randomly selected university student has taken any course in law, and \(V\) be the event that a randomly selected university student has taken any course in visual arts. Suppose that \(P(L) = 0.691\), \(P(V) = 0.139\), and \(P(L \cup V) = 0.729\). What is the probability that the student has taken a course in visual arts but not in law?

(Question ID: 0828639713)

Let \(B\) be the event that a randomly selected university student has taken any course in biology, and \(J\) be the event that a randomly selected university student has taken any course in journalism. Suppose that \(P(B) = 0.351\), \(P(J) = 0.485\), and \(P(B \cap J) = 0.313\). What is the probability that the student has taken a course in journalism but not in biology?

(Question ID: 0108732007)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(Q) = 0.131\), \(P(O) = 0.77\), and \(P(Q \cup O) = 0.816\). What is the probability that the student has taken either a course in both quantum mechanics and oceanography?

(Question ID: 0457574417)

Let \(B\) be the event that a randomly selected university student has taken any course in biology, and \(T\) be the event that a randomly selected university student has taken any course in theater. Suppose that \(P(B) = 0.858\), \(P(T) = 0.796\), and \(P(B \cap T) = 0.07\). What is the probability that the student has taken a course in biology but not in theater?

(Question ID: 0202999725)

Let \(P\) be the event that a randomly selected university student has taken any course in psychology, and \(J\) be the event that a randomly selected university student has taken any course in journalism. Suppose that \(P(P) = 0.577\), \(P(J) = 0.725\), and \(P(P \cup J) = 1.048\). What is the probability that the student has not taken a course in both psychology and journalism?

(Question ID: 0015281139)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(J\) be the event that a randomly selected university student has taken any course in journalism. Suppose that \(P(S) = 0.47\), \(P(J) = 0.422\), and \(P(S \cap J) = 0.129\). What is the probability that the student has taken a course in statistics but not in journalism?

(Question ID: 0270255692)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(P\) be the event that a randomly selected university student has taken any course in psychology. Suppose that \(P(S) = 0.496\), \(P(P) = 0.464\), and \(P(S \cap P) = 0.251\). What is the probability that the student has taken either a course in either statistics or psychology?

(Question ID: 0105771626)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(Q) = 0.393\), \(P(O) = 0.78\), and \(P(Q \cap O) = 0.295\). What is the probability that the student has taken either a course in either quantum mechanics or oceanography?

(Question ID: 0358820843)

Let \(H\) be the event that a randomly selected university student has taken any course in history, and \(P\) be the event that a randomly selected university student has taken any course in psychology. Suppose that \(P(H) = 0.389\), \(P(P) = 0.352\), and \(P(H \cap P) = 0.204\). What is the probability that the student has taken a course in psychology but not in history?

(Question ID: 0324225617)

Let \(I\) be the event that a randomly selected university student has taken any course in international relations, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(I) = 0.167\), \(P(O) = 0.742\), and \(P(I \cup O) = 0.795\). What is the probability that the student has taken a course in oceanography but not in international relations?

(Question ID: 0513112825)

Let \(V\) be the event that a randomly selected university student has taken any course in visual arts, and \(M\) be the event that a randomly selected university student has taken any course in music. Suppose that \(P(V) = 0.863\), \(P(M) = 0.525\), and \(P(V \cap M) = 0.303\). What is the probability that the student has taken a course in visual arts but not in music?

(Question ID: 0394859735)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(F\) be the event that a randomly selected university student has taken any course in french. Suppose that \(P(S) = 0.372\), \(P(F) = 0.773\), and \(P(S \cap F) = 0.199\). What is the probability that the student has taken a course in statistics but not in french?

(Question ID: 0426861956)

Let \(D\) be the event that a randomly selected university student has taken any course in design, and \(U\) be the event that a randomly selected university student has taken any course in urban planning. Suppose that \(P(D) = 0.152\), \(P(U) = 0.121\), and \(P(D \cap U) = 0.068\). What is the probability that the student has taken a course in urban planning but not in design?

(Question ID: 0098363993)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(F\) be the event that a randomly selected university student has taken any course in french. Suppose that \(P(Q) = 0.698\), \(P(F) = 0.595\), and \(P(Q \cup F) = 1.003\). What is the probability that the student has taken a course in quantum mechanics but not in french?

(Question ID: 0778981898)

Let \(K\) be the event that a randomly selected university student has taken any course in kinesiology, and \(I\) be the event that a randomly selected university student has taken any course in international relations. Suppose that \(P(K) = 0.14\), \(P(I) = 0.774\), and \(P(K \cap I) = 0.068\). What is the probability that the student has not taken a course in either of kinesiology or international relations?

(Question ID: 0267030643)

Let \(S\) be the event that a randomly selected university student has taken any course in statistics, and \(D\) be the event that a randomly selected university student has taken any course in design. Suppose that \(P(S) = 0.349\), \(P(D) = 0.693\), and \(P(S \cup D) = 0.94\). What is the probability that the student has taken a course in statistics but not in design?

(Question ID: 0101285460)

Let \(A\) be the event that a randomly selected university student has taken any course in art history, and \(I\) be the event that a randomly selected university student has taken any course in international relations. Suppose that \(P(A) = 0.427\), \(P(I) = 0.205\), and \(P(A \cup I) = 0.469\). What is the probability that the student has taken a course in art history but not in international relations?

(Question ID: 0847457667)

Let \(I\) be the event that a randomly selected university student has taken any course in international relations, and \(C\) be the event that a randomly selected university student has taken any course in chemistry. Suppose that \(P(I) = 0.314\), \(P(C) = 0.261\), and \(P(I \cap C) = 0.127\). What is the probability that the student has not taken a course in either of international relations or chemistry?

(Question ID: 0708501292)

Let \(T\) be the event that a randomly selected university student has taken any course in theater, and \(F\) be the event that a randomly selected university student has taken any course in french. Suppose that \(P(T) = 0.607\), \(P(F) = 0.1\), and \(P(T \cap F) = 0.067\). What is the probability that the student has taken a course in theater but not in french?

(Question ID: 0899283672)

Let \(A\) be the event that a randomly selected university student has taken any course in art history, and \(D\) be the event that a randomly selected university student has taken any course in design. Suppose that \(P(A) = 0.47\), \(P(D) = 0.87\), and \(P(A \cup D) = 0.93\). What is the probability that the student has not taken a course in both art history and design?

(Question ID: 0718195761)

Let \(V\) be the event that a randomly selected university student has taken any course in visual arts, and \(G\) be the event that a randomly selected university student has taken any course in geography. Suppose that \(P(V) = 0.53\), \(P(G) = 0.138\), and \(P(V \cap G) = 0.079\). What is the probability that the student has taken a course in geography but not in visual arts?

(Question ID: 0143343213)

Let \(A\) be the event that a randomly selected university student has taken any course in art history, and \(B\) be the event that a randomly selected university student has taken any course in biology. Suppose that \(P(A) = 0.131\), \(P(B) = 0.368\), and \(P(A \cup B) = 0.431\). What is the probability that the student has taken either a course in both art history and biology?

(Question ID: 0299081096)

Let \(B\) be the event that a randomly selected university student has taken any course in biology, and \(C\) be the event that a randomly selected university student has taken any course in chemistry. Suppose that \(P(B) = 0.75\), \(P(C) = 0.303\), and \(P(B \cup C) = 0.988\). What is the probability that the student has not taken a course in both biology and chemistry?

(Question ID: 0405931000)

Let \(M\) be the event that a randomly selected university student has taken any course in music, and \(D\) be the event that a randomly selected university student has taken any course in design. Suppose that \(P(M) = 0.566\), \(P(D) = 0.221\), and \(P(M \cup D) = 0.614\). What is the probability that the student has taken either a course in both music and design?

(Question ID: 0991963979)

Let \(R\) be the event that a randomly selected university student has taken any course in religion, and \(A\) be the event that a randomly selected university student has taken any course in art history. Suppose that \(P(R) = 0.726\), \(P(A) = 0.196\), and \(P(R \cap A) = 0.157\). What is the probability that the student has not taken a course in either of religion or art history?

(Question ID: 0623271498)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(B\) be the event that a randomly selected university student has taken any course in biology. Suppose that \(P(Q) = 0.507\), \(P(B) = 0.152\), and \(P(Q \cup B) = 0.547\). What is the probability that the student has not taken a course in both quantum mechanics and biology?

(Question ID: 0858359376)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(E\) be the event that a randomly selected university student has taken any course in english. Suppose that \(P(Q) = 0.635\), \(P(E) = 0.654\), and \(P(Q \cup E) = 1.064\). What is the probability that the student has taken either a course in both quantum mechanics and english?

(Question ID: 0688122892)

Let \(L\) be the event that a randomly selected university student has taken any course in law, and \(V\) be the event that a randomly selected university student has taken any course in visual arts. Suppose that \(P(L) = 0.842\), \(P(V) = 0.317\), and \(P(L \cap V) = 0.134\). What is the probability that the student has not taken a course in either of law or visual arts?

(Question ID: 0698951221)

Let \(H\) be the event that a randomly selected university student has taken any course in history, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(H) = 0.106\), \(P(O) = 0.6\), and \(P(H \cap O) = 0.077\). What is the probability that the student has taken a course in oceanography but not in history?

(Question ID: 0870521544)

Let \(I\) be the event that a randomly selected university student has taken any course in international relations, and \(D\) be the event that a randomly selected university student has taken any course in design. Suppose that \(P(I) = 0.559\), \(P(D) = 0.751\), and \(P(I \cap D) = 0.323\). What is the probability that the student has taken a course in international relations but not in design?

(Question ID: 0750412833)

Let \(U\) be the event that a randomly selected university student has taken any course in urban planning, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(U) = 0.641\), \(P(O) = 0.525\), and \(P(U \cap O) = 0.079\). What is the probability that the student has taken a course in urban planning but not in oceanography?

(Question ID: 0272975372)

Let \(Q\) be the event that a randomly selected university student has taken any course in quantum mechanics, and \(K\) be the event that a randomly selected university student has taken any course in kinesiology. Suppose that \(P(Q) = 0.504\), \(P(K) = 0.219\), and \(P(Q \cap K) = 0.178\). What is the probability that the student has taken a course in quantum mechanics but not in kinesiology?

(Question ID: 0674877122)

Let \(F\) be the event that a randomly selected university student has taken any course in french, and \(A\) be the event that a randomly selected university student has taken any course in art history. Suppose that \(P(F) = 0.427\), \(P(A) = 0.516\), and \(P(F \cup A) = 0.661\). What is the probability that the student has taken a course in french but not in art history?

(Question ID: 0181585348)

Let \(F\) be the event that a randomly selected university student has taken any course in french, and \(O\) be the event that a randomly selected university student has taken any course in oceanography. Suppose that \(P(F) = 0.502\), \(P(O) = 0.707\), and \(P(F \cup O) = 0.877\). What is the probability that the student has taken a course in french but not in oceanography?

(Question ID: 0270597583)

Let \(G\) be the event that a randomly selected university student has taken any course in geography, and \(I\) be the event that a randomly selected university student has taken any course in international relations. Suppose that \(P(G) = 0.823\), \(P(I) = 0.293\), and \(P(G \cup I) = 0.939\). What is the probability that the student has taken either a course in both geography and international relations?

(Question ID: 0100681147)

Let \(K\) be the event that a randomly selected university student has taken any course in kinesiology, and \(J\) be the event that a randomly selected university student has taken any course in journalism. Suppose that \(P(K) = 0.861\), \(P(J) = 0.531\), and \(P(K \cap J) = 0.34\). What is the probability that the student has taken a course in journalism but not in kinesiology?

(Question ID: 0415694600)

Let \(N\) be the event that a randomly selected university student has taken any course in neuroscience, and \(S\) be the event that a randomly selected university student has taken any course in statistics. Suppose that \(P(N) = 0.426\), \(P(S) = 0.799\), and \(P(N \cap S) = 0.225\). What is the probability that the student has taken a course in neuroscience but not in statistics?

(Question ID: 0844346665)

Let \(H\) be the event that a randomly selected university student has taken any course in history, and \(L\) be the event that a randomly selected university student has taken any course in law. Suppose that \(P(H) = 0.691\), \(P(L) = 0.626\), and \(P(H \cup L) = 1.075\). What is the probability that the student has taken a course in history but not in law?

(Question ID: 0054461231)

Let \(P\) be the event that a randomly selected university student has taken any course in psychology, and \(F\) be the event that a randomly selected university student has taken any course in french. Suppose that \(P(P) = 0.382\), \(P(F) = 0.288\), and \(P(P \cup F) = 0.411\). What is the probability that the student has not taken a course in both psychology and french?

(Question ID: 0781142314)

Self Assessment 3.4

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 40.8% of trains have traffic considered light and that 29.3% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0303351515)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 12.7% of trains have traffic considered light and that 47.7% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0458510174)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 12.5% of hotels are budget and that 50.7% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0369012767)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 11.4% of trains have traffic considered light and that 44.4% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0091214176)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 6.8% of submissions are scored needs improvement and that 56.8% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0324363628)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 29.6% of investments are low risk and that 41.9% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0336952340)

Patients with a particular illness are categorized into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 69.3% of patients are low risk and that 12.6% of patients are moderate risk.

Consider a patient that is randomly selected.

1. What is the probability that the patient is “high risk”?
2. What is the probability that the patient is not “low risk”?
3. What is the probability that the patient is either “low risk” or “moderate risk”?
4. What is the probability that the patient is both “low risk” and “moderate risk”?

(Question ID: 0881220439)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 30.6% of investments are low risk and that 10.2% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0732931182)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 45.7% of hotels are budget and that 17.5% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0648484598)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 71.6% of submissions are scored needs improvement and that 8.1% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0678704294)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 16.8% of investments are low risk and that 44.9% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0394185287)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 27.5% of submissions are scored needs improvement and that 52.4% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0869568195)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 16.9% of investments are low risk and that 52.2% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0622756964)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 18.8% of submissions are scored needs improvement and that 27.1% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0301890878)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 22% of customers are dissatisfied and that 44.6% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0822236064)

Patients with a particular illness are categorized into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 35.4% of patients are low risk and that 31.2% of patients are moderate risk.

Consider a patient that is randomly selected.

1. What is the probability that the patient is “high risk”?
2. What is the probability that the patient is not “low risk”?
3. What is the probability that the patient is either “low risk” or “moderate risk”?
4. What is the probability that the patient is both “low risk” and “moderate risk”?

(Question ID: 0515560155)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 7.3% of submissions are scored needs improvement and that 11.7% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0049371959)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 56.8% of customers are dissatisfied and that 37.7% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0612936733)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 57.2% of trains have traffic considered light and that 31.5% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0763729930)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 17.7% of customers are dissatisfied and that 53.3% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0694512320)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 56.9% of hotels are budget and that 29.8% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0328885274)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 5.7% of submissions are scored needs improvement and that 6% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0067186262)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 44.8% of investments are low risk and that 36.8% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0120316759)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 23.1% of hotels are budget and that 21.4% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0039404027)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 45.2% of submissions are scored needs improvement and that 22.3% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0211965364)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 28.6% of hotels are budget and that 37% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0372488061)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 81.7% of hotels are budget and that 0.5% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0255287717)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 71.8% of trains have traffic considered light and that 1.7% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0319050189)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 24.5% of hotels are budget and that 8.9% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0827714487)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 33.4% of investments are low risk and that 7% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0804489805)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 11.2% of customers are dissatisfied and that 68.2% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0705180564)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 18.8% of hotels are budget and that 14.7% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0184763664)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 13.7% of hotels are budget and that 79% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0811569378)

Patients with a particular illness are categorized into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 21% of patients are low risk and that 40% of patients are moderate risk.

Consider a patient that is randomly selected.

1. What is the probability that the patient is “high risk”?
2. What is the probability that the patient is not “low risk”?
3. What is the probability that the patient is either “low risk” or “moderate risk”?
4. What is the probability that the patient is both “low risk” and “moderate risk”?

(Question ID: 0390701137)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 25.4% of hotels are budget and that 68.5% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0605786154)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 9.2% of customers are dissatisfied and that 57.2% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0854206092)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 28.7% of submissions are scored needs improvement and that 0.9% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0196250009)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 5.1% of customers are dissatisfied and that 58.5% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0623352874)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 31.6% of investments are low risk and that 52% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0370053750)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 52.8% of trains have traffic considered light and that 5.7% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0223096894)

Hotels are rated on a three tier scale: budget, mid-range, and luxury.

Suppose that 81.6% of hotels are budget and that 6.4% of hotels are mid-range.

Consider a hotel that is randomly selected.

1. What is the probability that the hotel is “luxury”?
2. What is the probability that the hotel is not “budget”?
3. What is the probability that the hotel is either “budget” or “mid-range”?
4. What is the probability that the hotel is both “budget” and “mid-range”?

(Question ID: 0701585969)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 19.7% of customers are dissatisfied and that 11.1% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0375115591)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 26.4% of submissions are scored needs improvement and that 49.3% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0185212892)

Student submissions are qualitatively graded on a three-point scale: needs improvement, meets expectations, and exceeds expectations.

Suppose that 5.5% of submissions are scored needs improvement and that 65.4% of submissions are scored meets expectations.

Consider a submission that is randomly selected.

1. What is the probability that the submission is scored “exceeds expectations”?
2. What is the probability that the submission is scored not “needs improvement”?
3. What is the probability that the submission is scored either “needs improvement” or “meets expectations”?
4. What is the probability that the submission is scored both “needs improvement” and “meets expectations”?

(Question ID: 0229444852)

An investor categorizes prospective investments into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 61.1% of investments are low risk and that 12% of investments are moderate risk.

Consider an investment that is randomly selected.

1. What is the probability that the investment is “high risk”?
2. What is the probability that the investment is not “low risk”?
3. What is the probability that the investment is either “low risk” or “moderate risk”?
4. What is the probability that the investment is both “low risk” and “moderate risk”?

(Question ID: 0172260305)

Patients with a particular illness are categorized into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 44.5% of patients are low risk and that 30.4% of patients are moderate risk.

Consider a patient that is randomly selected.

1. What is the probability that the patient is “high risk”?
2. What is the probability that the patient is not “low risk”?
3. What is the probability that the patient is either “low risk” or “moderate risk”?
4. What is the probability that the patient is both “low risk” and “moderate risk”?

(Question ID: 0559707919)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 31.9% of customers are dissatisfied and that 21.8% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0954734289)

Patients with a particular illness are categorized into three levels of risk: low risk, moderate risk, and high risk.

Suppose that 14.1% of patients are low risk and that 53.3% of patients are moderate risk.

Consider a patient that is randomly selected.

1. What is the probability that the patient is “high risk”?
2. What is the probability that the patient is not “low risk”?
3. What is the probability that the patient is either “low risk” or “moderate risk”?
4. What is the probability that the patient is both “low risk” and “moderate risk”?

(Question ID: 0183229345)

Customers at a particular store have their satisfaction recorded across three categories: dissatisfied, neutral, and satisfied.

Suppose that 38.1% of customers are dissatisfied and that 34.1% of customers are neutral.

Consider a customer that is randomly selected.

1. What is the probability that the customer is “satisfied”?
2. What is the probability that the customer is not “dissatisfied”?
3. What is the probability that the customer is either “dissatisfied” or “neutral”?
4. What is the probability that the customer is both “dissatisfied” and “neutral”?

(Question ID: 0280628159)

The traffic on commuter trains is categorized into one of three categories: light, moderate, and heavy.

Suppose that 66.3% of trains have traffic considered light and that 22.4% of trains have traffic considered moderate.

Consider a train that is randomly selected.

1. What is the probability that the train traffic is considered “heavy”?
2. What is the probability that the train traffic is considered not “light”?
3. What is the probability that the train traffic is considered either “light” or “moderate”?
4. What is the probability that the train traffic is considered both “light” and “moderate”?

(Question ID: 0468785218)

Self Assessment 3.5

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a paperback.

How many ways can this be done?

(Question ID: 0539854366)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, and such that each paperback is between two hardcovers.

How many ways can this be done?

(Question ID: 0795829595)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0071197282)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a hardcover and the last book is a paperback.

How many ways can this be done?

(Question ID: 0584080199)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0566568236)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together.

How many ways can this be done?

(Question ID: 0284306833)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0227707483)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but all the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0483804098)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0489679097)

It is required to place \(8\) hardcovers and \(7\) paperbacks onto a bookshelf, where every book is distinct.

How many ways can this be done?

(Question ID: 0881116084)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct.

How many ways can this be done?

(Question ID: 0395978203)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a hardcover and the last book is a paperback.

How many ways can this be done?

(Question ID: 0287499129)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where each hardcover is identical, but the paperbacks are distinct.

How many ways can this be done?

(Question ID: 0336409700)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a hardcover and the last book is a paperback.

How many ways can this be done?

(Question ID: 0736777941)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, and such that each paperback is between two hardcovers.

How many ways can this be done?

(Question ID: 0666203358)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0692786261)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0694081537)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a paperback and the last book is a hardcover.

How many ways can this be done?

(Question ID: 0891681966)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0006501430)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a paperback and the last book is a hardcover.

How many ways can this be done?

(Question ID: 0197895457)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a hardcover and the last book is a paperback.

How many ways can this be done?

(Question ID: 0319575028)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where each paperback is identical and each hardcover is identical.

How many ways can this be done?

(Question ID: 0202872667)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a hardcover.

How many ways can this be done?

(Question ID: 0690370173)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together.

How many ways can this be done?

(Question ID: 0183430058)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where each paperback is identical and each hardcover is identical.

How many ways can this be done?

(Question ID: 0957976781)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a paperback and the last book is a hardcover.

How many ways can this be done?

(Question ID: 0859141635)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together.

How many ways can this be done?

(Question ID: 0140880113)

It is required to place \(8\) hardcovers and \(7\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a paperback and the last book is a hardcover.

How many ways can this be done?

(Question ID: 0242136753)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together.

How many ways can this be done?

(Question ID: 0382605116)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0240319337)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but all the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0361422804)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0916748515)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where every book is distinct, and such that each paperback is between two hardcovers.

How many ways can this be done?

(Question ID: 0145659093)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0658959506)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where every book is distinct, but all the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0402274856)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a hardcover.

How many ways can this be done?

(Question ID: 0929543042)

It is required to place \(7\) hardcovers and \(6\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0676748067)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a paperback.

How many ways can this be done?

(Question ID: 0918951536)

It is required to place \(8\) hardcovers and \(7\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a hardcover.

How many ways can this be done?

(Question ID: 0291843947)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, and such that each paperback is between two hardcovers.

How many ways can this be done?

(Question ID: 0394628562)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a paperback.

How many ways can this be done?

(Question ID: 0238937764)

It is required to place \(9\) hardcovers and \(8\) paperbacks onto a bookshelf, where every book is distinct, but the first book is a paperback and the last book is a hardcover.

How many ways can this be done?

(Question ID: 0311297413)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where each paperback is identical and each hardcover is identical.

How many ways can this be done?

(Question ID: 0215715292)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0307689190)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where every book is distinct, but the first and last should be a paperback.

How many ways can this be done?

(Question ID: 0474729511)

It is required to place \(4\) hardcovers and \(3\) paperbacks onto a bookshelf, where every book is distinct, but all the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0127234045)

It is required to place \(6\) hardcovers and \(5\) paperbacks onto a bookshelf, where each paperback is identical, but the hardcovers are distinct.

How many ways can this be done?

(Question ID: 0674715054)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where each paperback is identical and each hardcover is identical.

How many ways can this be done?

(Question ID: 0776070668)

It is required to place \(5\) hardcovers and \(4\) paperbacks onto a bookshelf, where every book is distinct.

How many ways can this be done?

(Question ID: 0436683332)

It is required to place \(8\) hardcovers and \(7\) paperbacks onto a bookshelf, where every book is distinct, but all the paperbacks are grouped together and the hardcovers are grouped together.

How many ways can this be done?

(Question ID: 0071798345)

References

Kahneman, Daniel, and Amos Tversky. 1972. “Subjective Probability: A Judgment of Representativeness.” Cognitive Psychology 3 (3): 430–54.

---

1. Or else conclude that I was mistaken and maybe should not be teaching probability.

2. One of the most famous quotes from a statistician was a thought shared by John Tukey, stating “The best thing about being a statistician is that you get to play in everyone’s backyard.” This is a common refrain, and one rooted in truth. Statistics is everywhere, across every field of human inquiry, and can help us make sense of everything from the trivial to the deeply important.

3. This does not help to explain why we use urns so much, of course. When was the last time any of us drew a ball from an urn?

4. Note that, when we have a set, using the absolute value symbols \(|\cdot|\) stands for the cardinality of the set. Cardinality is just a fancy way of saying the size or the number of elements that the set has in it.

5. A quantity which in the equally likely outcome framework, we know exactly.

6. The sample function can also be used without equally likely events by specifying a vector of probabilities, however, this is a less common use case.

7. For instance, the Queen of spades being drawn.

8. This is actually a scenario where our instincts may lead us awry in some situations. Consider the following from Kahneman and Tversky (1972): Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. Which is more probable? (a) Linda is a bank teller, or (b) Linda is a bank teller and is active in the feminist movement. A majority of respondents rate (b) as being more probable, even though (a) is contained in (b).

9. These rules, which we call “properties” are formally known as “axioms”.

10. What would it mean to have a negative probability? It is perhaps a more interesting question than it seems at first glance. It is a topic that has come up in some pretty strange places and, while it is not presently sensible to call them “probabilities” in a traditional sense, there are interesting results which follow.

11. Note: if this is not yet clear to you, that’s okay! In the very next section we begin to discuss how to count the possible combinations in these types of scenarios.

12. Suppose that \(d_1 = 2\) and \(d_2 = 4\). Then here, the dice can match when they show either \(1\) or \(2\), but if the second die shows \(3\) or \(4\) there is no possibility of having a match at all.

13. Factorials are exciting because they always look like they are shouting!

14. It is somewhat interesting to note how large these values get relatively quickly. This is a comparatively small question: only \(10\) people with \(10\) drinks and \(10\) snacks. If you consider any counting problem with a larger number of items, these problems quickly grow to be intensely complex. For instance, a count of my main home book collection reveals \(376\) of them. To order these would give \(376!\) possible orderings. In decimal representation this is \[4.992244775852435618292576458782762114148884082811840265632\dots\times10^{806}.\] This is an \(807\) digit long number. This is an incomprehensibly large number. This number is \(8×10^{726}\) times larger than the number of atoms in the universe. That is, if every atom in the universe were given some arrangements of books to hold onto, they would need to hold \(8×10^{726}\) of them in order for all of the arrangements to be held. I point this out because combinatorics explodes in this way. Even simple problems grow out of hand very, very quickly. This is where comfort with the algebraic tools is required, rather than a reliance on intuition. There is simply no way to have intuition regarding the scope of these numbers, at least, not without a lot of practice.

15. Imagine I am placing books on my shelf. With \(3\) books there are \(3! = 6\) ways my shelf can look at the end. With \(2\) books there are \(2! = 2\) ways my shelf can look at the end. With \(1\) book there are \(1! = 1\) ways my shelf can look at the end. With \(0\) books there are \(0! = 1\) ways my shelf can look at the end.

16. Note, this does not help us with the factorials of negative numbers, nor of fractional numbers. Factorials can be extended to these in sensible ways, but these are not for combinatorial purposes and are no longer “factorials” exactly.

17. In fact, the reason that there are \(2\) ways of doing this with the book with \(2\) copies is since \(2! = 2\).

18. This is still a deeply unintuitive result to me. To me it feels like it should be harder to get a nice ordering of cards all in a row than it is to find ones of the same suit. And yet, it is about twice as likely to have the straights. Now, if you think about this deeply, it makes a lot of sense: there is a lot more leeway in selecting the straight than the flush. However, my brain refuses to accept this as intuitive. This is something that can often occur in probability questions where the true results can be far from what we would expect. An interesting question is how long does a straight have to be to be less likely than a flush of the same length. Note that the number of ways of choosing a flush will always be \(4\times\binom{13}{k}\), and the number of ways of forming a straight will always be \(10\times 4^k\). If we consider \(k\) from \(1\) to \(13\), we can take the ratios of these to see just how much more (or less) likely a straight is. Doing this gives: k=1 gives 0.769. k=2 gives 0.513. k=3 gives 0.559. k=4 gives 0.895. k=5 gives 1.989. k=6 gives 5.967. k=7 gives 23.869. k=8 gives 127.304. k=9 gives 916.587. k=10 gives 9165.874. k=11 gives 134432.821. k=12 gives 3226387.692. k=13 gives 167772160. Up to (and including) \(4\) cards the straight is indeed harder to achieve. However, this does not last long!