9 Continuous Random Variables

Our discussions of probability distributions and their summaries have focused entirely on discrete random variables. To recap, a discrete random variable is any random numeric quantity that can take on a countable number of values. Discrete random variables are defined in contrast to continuous random variables, which take on values over the span of intervals in uncountably large sets. Suppose that \(X\) can take any real number between \(0\) and \(1\). There is no way to enumerate the set of possible values for this random quantity, and so it must not be discrete.

Many quantities of interest are better treated as a continuous quantity rather than a discrete one even when this is not technically correct. For instance, time measured in seconds is often best thought of as continuous, even though any stop watch used to grab these measurements will have some limit to the precision with which they can measure. Similarly, lengths and heights will often be better treated as continuous quantities, even though any measuring device will necessarily have some minimal threshold after which it cannot discern distances. Thus, deciding whether a quantity is continuous or discrete is sometimes a judgment call. In general discrete quantities are harder to work with when the set of possibilities is very large. In these cases, not much is lost by treating the random variables as though they were continuous. This distinction is another area which requires the active development of intuition, but once present, the distinctions become second nature.¹

9.1 Continuous Versus Discrete

Distinguishing whether a random quantity is continuous or discrete is crucial as, broadly speaking, the two types of quantities are treated differently. The same underlying ideas are present, but the distinctions between the two settings require some careful thought. The use of continuous random variables necessitates an understanding of introductory calculus. These course notes are designed to be understood without any experience in calculus, and as a result, we will first present continuous random variables in general, without the need for calculus. Additional sections containing the technical details follow. Despite requiring calculus to be completely understood, continuous random variables are the dominant type of random variables outside of introductory courses. As a result, understanding the distinctions, and becoming familiar with how they are to be manipulated is an important skill.

The key difference between discrete and continuous random variables is that, for discrete random variables the behaviour is governed by assessing \(P(X=x)\) for all possible values of \(x\), while for continuous random variables \(P(X=x)=0\) for every value of \(x\). This is likely a surprising statement, and as such it is worth reiterating. With discrete random variables we discussed how all of the probabilistic behaviour is governed by the probability mass function. This is defined as \(p_X(x) = P(X=x)\). If \(X\) is a continuous random variable, we must have \(P(X=x) = 0\). Correspondingly, continuous random variables do not have probability mass functions, and to understand the behaviour of these random variables we must use other quantities.

Singleton Probabilities with Continuous Random Variables

While the fact that \(P(X=x) = 0\) may seem unintuitive at first glance, it is worth exploring this even further. The nature of a continuous random variable is such that there is no possible way to enumerate all of the values that are possible to be realized by the random quantity. Suppose that we take a set of countably many possible observations and gave each of these a probability of greater than \(0\) of occurring. Even if we take an infinite number of them, there will still be an uncountably infinite number of events in the sample space that we have not accounted for. We know that the total probability of the sample space must be \(1\), and so we must have the total probability of the first set of events being less than \(1\)².

Now suppose we take another set of countably many events, again giving each of them a positive probability. Once more the sum of all of these probabilities must be less than \(1\), and specifically, the sum of both sets must also be less than \(1\). Even after these two sets, there are still uncountably infinite events to go and so we continue this process. Because we always need the total probability to be \(1\) once all events have been accounted for, and because we will always have uncountably infinite events remaining to account for, we can never have a positive probability assigned to each event in a set of events. Even if we made the probability of each of these sets very, very small³ after some fixed number of countable events the probabilities would be greater than \(1\), which cannot happen. As such, each event itself must have \(0\) probability.

An alternative technique for understanding this intuition is to think about how unlikely it really would be to observe any specific value. Suppose that \(X\) takes values on the interval \([0,1]\). Recall that, when we defined probabilities, we discussed them as being the long run proportion of time that an event occurs. Take some event, say \(X=0.5\). Suppose that we took repeated measurements of \(X\) which are independent and identically distributed. Now suppose that at some point we exactly do observe \(X=0.5\). Should we expect that this will ever happen again? The next time we get near \(0.5\), might we instead observe \(0.51\) or \(0.49\) or \(0.5000000000000000001\) or any of the other uncountably infinite values in the very near vicinity of \(0.5\)? Each time that we make an observation the denominator of our proportion is growing, but if every value between \(0\) and \(1\) is truly possible, as time goes on the number of times that \(X=0.5\) must stay much, much smaller than the total number of trials. If we continue this off to infinity, in the limit, the probability must become \(0\).

This conclusion leads to a few different points. First, impossibility is not the same as probability \(0\). Impossible events do have probability \(0\), but possible events may also have probability \(0\). Events which are outside of the sample space are impossible. Events inside the sample space, even probability zero events, remain possible. Second, we require alternative mathematical tools for discussing the probability of events in a continuous setting. Ideally this would be analogous to a probability mass function, but would somehow function in the case of continuity.

9.2 Cumulative Distribution Functions

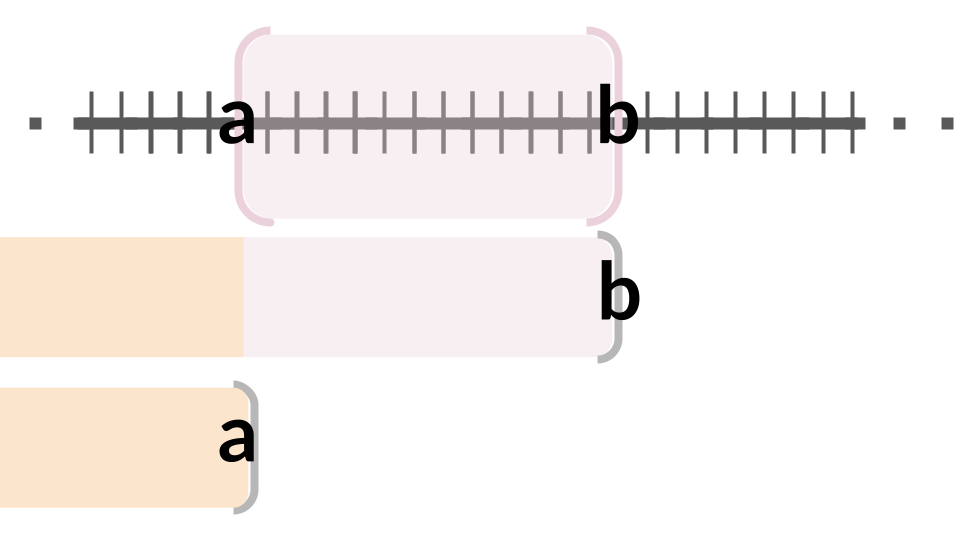
To begin building to the continuous analogue of the probability mass function, we will start by focusing on events that are easier to define in the continuous case. Suppose that \(X\) is defined on some continuous interval. Instead of thinking of events relating to \(X=x\), we instead turn our focus to events of the form \(X \in (a,b)\) for some interval defined by the endpoints \(a\) and \(b\). Now note that, relying only on our knowledge of probabilities relating to generic events, we can rewrite \(P(X\in(a,b))\) slightly. Specifically, \[\begin{align*} P(X\in(a,b)) &= 1 - P(X\not\in(a,b))\\ &= 1 - P(\{X < a\}\cup\{X > b\}) \\ &= 1 - \left(P(X < a) + P(X > b)\right)\\ &= 1 - P(X > b) - P(X < a)\\ &= P(X < b) - P(X < a).\end{align*}\]

Figure 9.1: A number line showcasing the interval \((a,b)\) and demonstrating how you can take everything less than \(b\) and remove all that is less than \(a\) to be left with only \((a,b)\).

In words we know that the probability that \(X\) falls into any particular interval is given by the probability that it is less than the upper bound of the interval minus the probability that it is less than the lower bound of the interval. Notice that \(X < a\) is an event, and if we knew how to assign probabilities to \(X<a\) for arbitrary \(a\), then we could assign probabilities to any interval. Also note that, even in the continuous case, it make sense to talk of \(P(X < a)\) for some value \(a\). These intervals will contain an uncountably infinite number of events, and as such, can certainly occur with greater than \(0\) probability.

Consider an example with \(X\) defined on \([0,1]\). In this case we know that \(P(X<1)=1\). Note that we could have written \(P(X \leq 1) = 1\), which may have been more obviously true. However, \(P(X\leq 1) = P(\{X<1\}\cup\{X=1\}) = P(X<1) + P(X=1)\) and we know that \(P(X=1)=0\). In the continuous case we do not need to worry whether we use \(X\leq a\) or \(X < a\), and we will interchange them throughout.

Example 9.1 (Charles and Sadie Wait for the Bus) Charles and Sadie are visiting a large city and are getting around via public transit while there. They are not quite familiar with the bus schedules yet, but they know that the bus they are waiting for will show up sometime in the next \(15\) minutes. They realize that this is a continuous random quantity, and decide to pass the time by trying to reason about how long they will be waiting for the bus to arrive. To do so, they make the assumption that the bus is equally likely to show at any point during this interval.

What is the probability that Charles and Sadie wait \(15\) or fewer minutes for the bus?
What is the probability that Charles and Sadie wait \(5\) or fewer minutes for the bus?
What is the probability that Charles and Sadie wait exactly \(7\) minutes for the bus?
What is the probability that Charles and Sadie wait between \(8\) and \(12\) minutes for the bus?
What is the probability that Charles and Sadie have to wait longer than \(13\) minutes for the bus?

Solution

Let \(X\) represent the amount of time that they wait for the bus.

If we trust their judgment, then they have claimed that they will wait between \(0\) and \(15\) minutes for the bus. As a result, \(P(X \leq 15) = 1\).
Here we can reason that if any time is equally likely for the bus to arrive, then the first \(5\) minutes must be as likely as the second interval of \(5\) minutes or the third. That is, in the first \(5\) minutes there is a total of \(\dfrac{5}{15} = \dfrac{1}{3}\) of the possible arrival times taken up, and so we must conclude that \(P(X \leq 5) = \dfrac{1}{3}\).
This would be \(P(X = 7)\). \(X\) is a continuous quantity, and so \(P(X = 7) = 0\).
We can reason through this in two different ways. First, we can use the property discussed above that \(P(X \in (8, 12)) = P(X \leq 12) - P(X\leq 8)\), and then use the same procedure as in (b). That gives \[P(X \in (8, 12)) = \dfrac{12}{15} - \dfrac{8}{15} = \dfrac{4}{15}.\] Alternatively, because each interval of the same length must be equally likely, we can reason that this is just a length \(4\) interval. Thus, it must have the same likelihood as any other length \(4\) interval, given by \(\dfrac{4}{15}\).
Note that, longer than \(13\) is the complement to less than \(13\). Thus, \[P(X \geq 13) = 1 - P(X \leq 13) = 1 - \dfrac{13}{15} = \dfrac{2}{15}.\]

The centrality of events of the form \(X \leq a\) prompts further consideration the cumulative distribution function (introduced in Definition 9.1).

Definition 9.1 (Cumulative Distribution Function) The cumulative distribution function of a random variable \(X\), typically denoted as \(F(x)\) or \(F_X(x)\), is defined as the function that gives the probability that the random variable is less than or equal to some threshold.

That is, \(F_X(x) = P(X \leq x)\). We may also refer to the cumulative distribution function simply as the distribution function.

Once we have defined the distribution function for a random variable, using the above derivation we are able to determine the probability associated with any events based on intervals. The cumulative distribution function for continuous random variables is central to nearly every probability calculation that is performed. In the discrete case, since it is simply the summation of the probability mass function, it tends to be a less useful quantity.

Suppose that, for a random variable \(X\), we know the cumulative distribution function. This knowledge permits the computation of any probability associated with the random variable. Consider some event defined in terms of \(X\) which we may wish to determine the probability of. We know that events are subsets of the sample space. Every one of these events can be written using our basic set operations (unions, intersections, and complements) applied to intervals of the form \((a,b)\) and sets of the form \(\{x\}\).⁴ The axioms of probability allow us to compute probabilities across the set operations. Further, our knowledge of the cumulative distribution function, the conversion of \(P(X \in (a,b))\) into \(F_X(b) - F_X(a)\), and the fact that \(P(X=x) = 0\) for all \(x\) gives all of the results we need to derive probabilities for these events.

Example 9.2 (Charles and Sadie’s Light Bulbs) Charles and Sadie decide that they need to replace some light bulbs. In their research online, a particular manufacturer of light bulbs, Bayesian Brights, lists the cumulative distribution function for the lifetime of their bulbs, in hours. The model Charles and Sadie are considering is said to have a lifetime (in hours) governed by \[F_X(x) = 1 - \exp\left(-\frac{x}{10000}\right).\]

What is the probability that a purchased lightbulb lasts for less than \(5000\) hours?
What is the probability that a purchased lightbulb lasts for between \(7500\) and \(12000\) hours?
What is the probability that a purchased lightbulb lasts for more than \(8000\) hours?

Solution

Using the given cumulative distribution function this can be calculated as \[P(X \leq 5000) = F(5000) = 1 - \exp\left(-\frac{5000}{10000}\right) = 1 - e^{-1/2} \approx 0.39346934.\]
Here we get \[\begin{multline*}P(X \in (7500,12000)) = P(X \leq 12000) - P(X\leq 7500) = F(12000) - F(7500) \\ = \exp\left(-0.75\right) - \exp\left(-1.2\right) \approx 0.171172341.\end{multline*}\]
We can convert this to be the complement event so that it is expressible in terms of the cumulative distribution function. That is, \(P(X \geq 8000) = 1 - P(X \leq 8000)\), and so \[P(X \geq 8000) = 1 - F(8000) = 1 - (1 - e^{-0.8}) = e^{-0.8} \approx 0.449328964.\]

9.3 The Probability Density Function

The distribution function will be the core object used to discuss the probabilistic behaviour of a continuous random variable. All of the behaviour of these random quantities will be described by the distribution function, and as such we will take the distribution function as a function which defines the distribution of a continuous random quantity. This is all that we need in order to analyze these random variables, however, it may be a little unsatisfying in contrast with the discrete case.

We had set out to find a quantity that paralleled the probability mass function. Instead, we concluded that the cumulative distribution function can be made to play the same role in terms of describing the behaviour of the random quantity. Still, it may be of interest for us to have a function which takes into account the relative likelihood of being near some value. Suppose, for instance, that for a random variable defined on \([0,1]\) we wanted to know how likely it was to be in the vicinity of \(X=0.5\). We could take a small number, say \(\delta = 0.01\) and calculate \[P(X\in(0.5-\delta,0.5+\delta)) = F(0.5+\delta)-F(0.5-\delta).\] This is perfectly well defined based on our discussions to this point. Now, suppose that \(\delta\) is small enough so that it is reasonable to assume that this probability is fairly evenly distributed throughout the interval. Then, if we wanted to assign a likelihood to each value, we could divide this total probability by the length of the interval, \(2\delta\). As a result, in this case, the probability that \(X\) is nearly \(0.5\) will be approximately given by the expression \[\dfrac{F(0.5+\delta)-F(0.5-\delta)}{2\delta}.\]

We had taken \(\delta=0.01\), but the same process could be applied for smaller and smaller \(\delta\), say \(0.001\) or \(0.0001\). Intuitively, as the size of this interval shrinks more and more we are getting a better and better estimate for the likelihood that the random variable is in the immediate vicinity of \(0.5\). Moreover, as \(\delta\) gets smaller and smaller our assumption of a uniform probability over the interval becomes more and more reasonable. Unfortunately, we cannot set \(\delta=0\), exactly. We can ask what happens in the limit as \(\delta\) continues to get smaller and smaller. This question is in the purview of calculus, and can in fact be answered. While working out the answer is beyond the scope of the course, we will provide the result anyway.⁵ The resulting function is called the probability density function, and is related to the cumulative distribution function through derivatives (and integrals).

Definition 9.2 (Probability Density Function) A random variable \(X\), with cumulative distribution function \(F(x)\), is further characterized by its probability density function, denoted \(f(x)\). The density function describes the relative likelihood of a random variable taking on values in a particular interval, and mirrors the behaviour of the probability mass function in the discrete case. Formally, the probability density function is equal to the derivative of the cumulative distribution function.

Roughly speaking, the density function evaluates how likely it is for a continuous quantity to be in a small neighbourhood of the given value. Critically, probability density functions do not give probabilities directly. In fact, probability density functions may give values that are greater than \(1\)!⁶ Still, if we see the shape of the probability density function, we can state how likely it is to make observations near the results of interest. We will often graph the density functions. The high points of the graph indicate regions with more probability than the regions of the graph which are lower. Again, the specific probability of any event \(X=x\) will always be \(0\), but some events fall in neighbourhoods which are more likely to observe than others.⁷

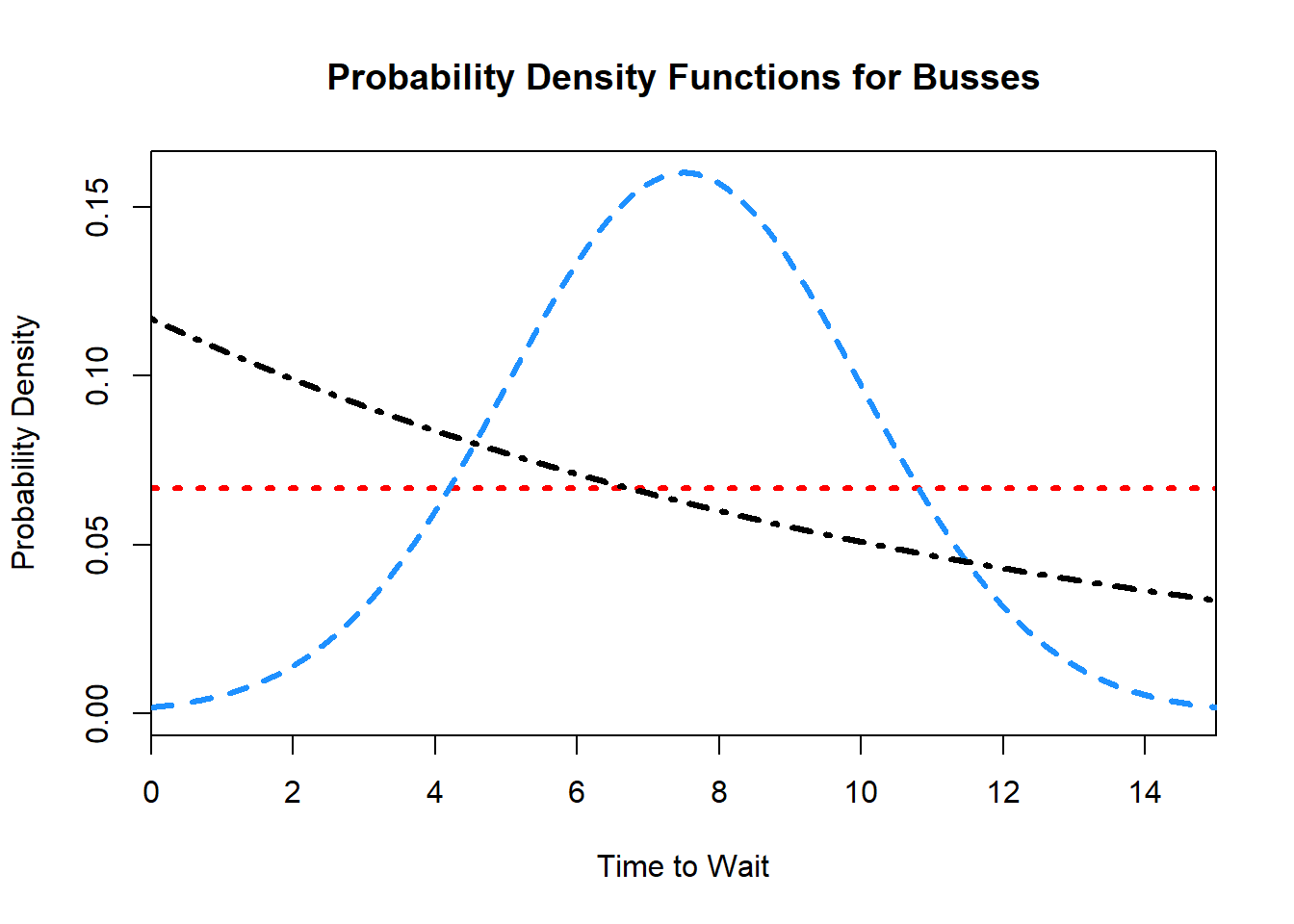
Example 9.3 (The Types of Busses in the City) After returning from their trip to the big city, Charles and Sadie are talking to their friend Garth, with a lot more experience in the matter. Garth explains that there are actually several different types of busses, with different arrival schedules over the \(15\) minute interval. Knowing that Charles and Sadie have started to learn about probability density functions, Garth draws out the following sketch, giving the probability density function for three different busses.

Which of the three buses is most likely to show up around the \(1\) minute mark?
Which of the three buses is most likely to show up around the \(6\) minute mark?
Which of the three buses is most likely to show up around the \(14\) minute mark?
Which bus is most likely to show up at \(10\) minutes exactly?
During which intervals would each of the buses be more likely than the other two to arrive?
Describe the behaviour of each of the three buses.

Solution

At \(x = 1\), the black density is higher than the red density which is higher than the blue density. This gives the relative ranking that arrivals around \(1\) minute or more likely for the black bus than red or blue.
At \(x = 6\), the blue density is higher than the red or black densities, which are roughly the same, and as such, it is the most likely bus to arrive in the vicinity of \(6\) minutes.
At \(14\), the red density is higher than the black density which is higher than the blue. This gives the relative ordering of likelihood of arrivals.
All buses have probability \(0\) of arriving at \(10\) minutes exactly since these are the densities for continuous random variables.
The black bus is most likely to arrive for times up until around \(4\) minutes, where the blue bus is then the most likely to arrive until around \(11\) minutes, where the red bus is most likely to arrive until the \(15\) minute mark.
The red bus has an equal probability of arriving across the full interval. The black bus is more likely to arrive near the start of the interval, slowly decaying in likelihood as time goes on, while remaining fairly likely at the \(15\) minute mark. The blue bus is very unlikely to take a very short period of time, or a very long period of time, and far more likely to sit in the middle of the possible interval.

Formally, the probability of any event of interest, say \(P(X \in [a,b])\) for some interval \([a,b]\), is given by the area under the probability density function. As a result, if the probability density function is plotted, then considering the area that is encompassed within any particular interval (or set of intervals) is equivalent to considering the probability that the random variable takes on a value in that range. This can be particularly useful when working with distributions and trying to get a sense of probabilities: drawing out the density function, and then highlighting the area of interest is an effective tool for understanding the probabilities that you are dealing with.

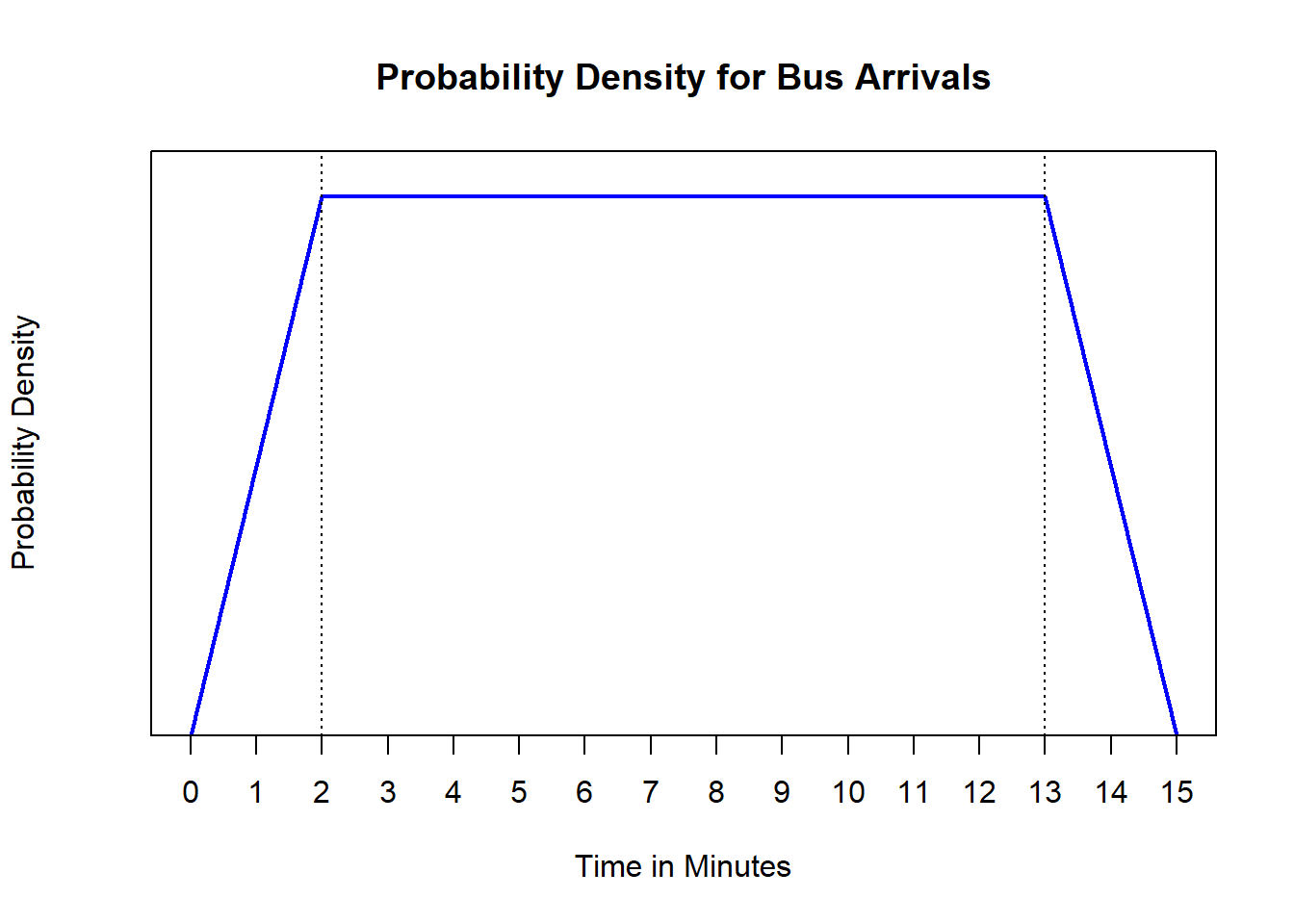
Example 9.4 (Non-Uniform Bus Arrivals) After some further investigation, Charles and Sadie decide that the uniformly arriving buses are not actually uniformly arriving. Instead, there is a lower probability of arriving, which increases for the first two minutes, then a uniform probability for the next eleven minutes, followed by a decreasing probability for the final two minutes. Charles draws a rough sketch of the density function that is expected.

At what value is the uniform portion of the probability density function depicted?
What is the probability that the bus arrives in the first two minutes?
What is the probability that the bus arrives in the final four minutes?

Solution

We know that the total probability must equal \(1\). Moreover, we know that the probability is given by the area under the curve. This area can be decomposed into two triangles, each with a base of \(2\) and an unknown height, \(h\), as well as a rectangle with a width of \(11\) and a height of \(h\). Thus, using geometric area formulae we get \[1 = 2\times\frac{1}{2}\times2\times h + 11\times h = 13h \implies h = \frac{1}{13}.\] Thus, the height will be \(\dfrac{1}{13}\).
The probability that the bus arrives in the first two minutes is the area under the curve between \(x = 0\) and \(x = 2\). This is given by a triangle with base \(2\) and height (from (a)) of \(\dfrac{1}{13}\). Thus, the probability that the bus arrives in the first two minutes is \(\dfrac{1}{2}\times2\times\dfrac{1}{13} = \dfrac{1}{13}\).
The probability that the bus arrives in the final four minutes is the same as the area under the curve between \(x=11\) and \(x=15\). This can either be computed as a trapezoidal area, or as the area of a rectangle plus that of a triangle. The triangle is equivalent to that computed for part (b), and the rectangle has a base of \(2\) and a height of \(\dfrac{1}{13}\), so that total the area is \[2\times\dfrac{1}{13} + \frac{1}{13} = \frac{3}{13}.\]

9.3.1 \(\int\) The Formal Mathematics for Continuous Random Variables

The use and understanding of a continuous cumulative distribution function can be done completely without calculus. However, even while motivating the idea of a probability density function we leaned on the concept of limits. The connection between the cumulative distribution function and the probability density function, as well as the use of the probability density function for the computation of probabilities, fundamentally relies on a grasp of differential and integral calculus. Consider the example outlined above that \(X\) is near \(0.5\). We argued that the probability is approximately \(2\delta f(0.5)\), where we defined \[f(0.5) = \lim_{\delta\to 0} \frac{F(0.5+\delta) - F(0.5-\delta)}{2\delta}.\] This is precisely the first principles definition of a derivative, meaning that \[f(0.5) = \left.\frac{d}{dx} F(x)\right|_{x=0.5} = F'(0.5).\]

Definition 9.3 (The Probability Density Function (Calculus)) The probability density function, denoted \(f(x)\), of a random variable \(X\) with cumulative distribution function \(F(x)\) is given by the first derivative of the cumulative distribution function, \[f(x) = \frac{d}{dx}F(x) = F'(x).\]

The interpretation remains the same: the probability density function gives a rough idea of how likely events near the desired outcome will be, but does not itself give probabilities. In order to get specific probabilities from the probability density function, we need to use the area under the curve.

Calculating Probabilities with Probability Density Functions

Suppose that we wish to calculate \(P(X \in (a, b))\) for a continuous random variable \(X\) with probability density function \(f(x)\). This is given by \[P(X \in (a,b)) = \int_{a}^b f(x)dx = F(a) - F(b),\] where \(F(x)\) is the cumulative distribution function. Suppose that, instead of a single interval, we wish to know the probability that \(A\) occurs, where \(A\) is an event that is comprised of the union of many intervals, say \[A = (a_1, b_1) \cup (a_2, b_2) \cup \cdots \cup (a_k, c_k).\] In this case we can apply the axiom of additivity to give, \[P(A) = \int_{a_1}^{b_1}f(x)dx + \int_{a_2}^{b_2}f(x)dx + \cdots + \int_{a_k}^{b_k}f(x)dx.\]

Using the fact that a probability density function is integrated in order to derive probability expressions, we can discuss the required features for a probability density function to be valid. These properties stem, fundamentally, from the requirements (under the axioms of probability) that \(P(E) \geq 0\) for all events and \(P(\mathcal{S}) = 1\).

Properties of a Probability Density Function

Non-negative: A valid probability density function, \(f(x)\), will be such that \(f(x) \geq 0\) for all real-valued \(x\).
Integrate to One: A valid probability density function will be such that \[\int_{-\infty}^\infty f(x)dx = 1.\]

These properties are analogous to the properties for a probability mass function, with one distinct difference: there is no requirement that the density function be less than or equal to \(1\). The rationale is that we require the complete area to be bounded above by \(1\) (in a property that is analogous to the sum-to-one constraint of probability mass functions), which occasionally results in probability density values above \(1\).

Given that the density function is the first derivative of the cumulative distribution function, we can apply the Fundamental Theorem of Calculus to conclude that the cumulative distribution function must be derived by integrating the density function. We can see this by noting that \(F(x) = P(X \in (-\infty, x))\), which we stated was given by integrating the density over \((-\infty, x)\).

Definition 9.4 (The Cumulative Distribution Function (Calculus)) The cumulative distribution function of a continuous random variable, \(X\), computes the probability that \(X\) is less than or equal to a threshold value \(x\). This can be computed as \[F(x) = \int_{-\infty}^x f(t)dt.\]

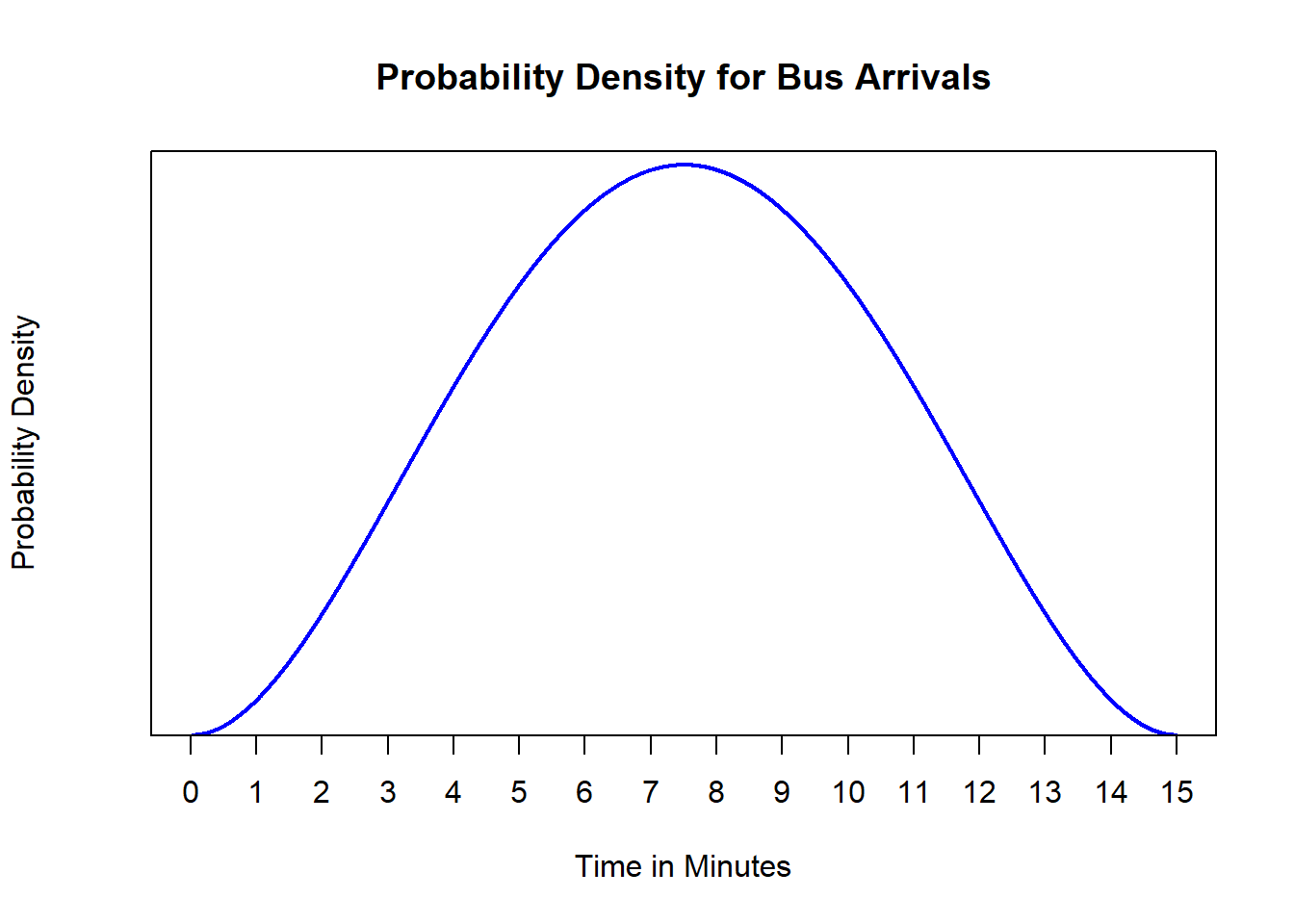
Example 9.5 (A More Complicated Density for the Bus) Charles and Sadie, while pleased with the added complexity afforded by the probability density function in Example 9.4, they are not sure that it is quite right. It seems that it is more likely that the bus arrives around the halfway point than it is at any other time throughout the interval. After playing around a bit, they propose the following curve, \[f(x) = \alpha\left(\frac{x}{15}\right)^2\left(1-\frac{x}{15}\right)^2, \quad x \in [0,15].\] This curve seems to have a shape that better tracks the expected arrivals.

What is the value of \(\alpha\) that renders this curve a valid probability density function?
What is the probability that the bus arrives in the first two minutes?
What is the probability that the bus arrives in the final four minutes?

Solution

We require both that the density function integrates to \(1\) and that it is always positive. Note that as long as \(\alpha > 0\), then \(f(x) \geq 0\), and so we will restrict attention only to solutions where \(\alpha > 0\). Beyond this, we require unit integration. That is, \[\begin{align*} 1 &= \int_{0}^{15} \alpha \left(\frac{x}{15}\right)^2\left(1-\frac{x}{15}\right)^2dx \\ &= 15\alpha\int_{0}^1 x^2(1 - x)^2dx \\ &= 15\alpha\int_{0}^1 x^2(1 - 2x + x^2)dx \\ &= 15\alpha\int_{0}^1 x^2 - 2x^3 + x^4dx \\ &= 15\alpha\left[\frac{x^3}{3} - \frac{x^4}{2} + \frac{x^5}{5}\right]_{x=0}^1 \\ &= 15\alpha\left[\frac{1}{3} - \frac{1}{2} + \frac{1}{5}\right] \\ &= 15\alpha\frac{1}{30} \\ &= \frac{\alpha}{2} \\ \implies \alpha = 2. \end{align*}\]
The probabilities can then be derived by integrating the density over the given area. As an alternative solution, you can integrate the density to derive the cumulative distribution function, and then use this to solve for the probabilities. Both techniques are shown.

To find \(F(x)\), we take \[\begin{align*} F(x) &= \int_{0}^{x} 2\left(\frac{t}{15}\right)^2\left(1-\frac{t}{15}\right)^2dt \\ &= 30\left[\frac{t^3}{3} - \frac{t^4}{2} + \frac{t^5}{5}\right]_{t=0}^{t=x/15} \\ &= 10\left(\frac{x}{15}\right)^3 - 15\left(\frac{x}{15}\right)^4 + 6\left(\frac{x}{15}\right)^5. \end{align*}\] Then, if we wish to find \[P(X \leq 2) = F(2) = 10\left(\frac{2}{15}\right)^3 - 15\left(\frac{2}{15}\right)^4 + 6\left(\frac{2}{15}\right)^5 = \frac{4864}{253125}.\]

Alternatively, we could have solved \[\int_{0}^{2} 2\left(\frac{t}{15}\right)^2\left(1-\frac{t}{15}\right)^2dt = \frac{4864}{253125},\] directly, through the same integration steps outlined.
We can use the cumulative distribution function found previously, or else directly integrate. To directly integrate you would solve \[\int_{11}^{15} 2\left(\frac{t}{15}\right)^2\left(1-\frac{t}{15}\right)^2dt,\] however, given that \(F(x)\) is known it is simpler to use that. This is given by \[P(11 \leq X \leq 15) = F(15) - F(11) = 1 - F(11) = 1 - \left(10\left(\frac{11}{15}\right)^3 - 15\left(\frac{11}{15}\right)^4 + 6\left(\frac{11}{15}\right)^5\right),\] which gives \[P(11 \leq X \leq 15) = \frac{30848}{253125}.\]

9.4 Using Continuous Distributions

With the exception of the previously indicated differences, continuous and discrete random variables are treated similarly. The tools to analyze them differ⁸, but the fundamentals remain the same. It is possible to compute expected values, medians, and modes, with roughly the same interpretations. It is possible to describe the range, interquartile range, and variance, with similar interpretations. The axioms of probability still underpin the manipulation and analysis of these random variables. The distinction is merely that in, place of elementary mathematics to complete the calculations, calculus is required.

9.4.1 \(\int\) Differences in Working With Discrete and Continuous Random Variables

Most of what was covered for discrete random variables will hold for continuous random variables as well, with the caveat that in the continuous case we replace summations with integrals. We have seen this to an extent already. In the discrete case, if a random variable \(X\) has probability mass function \(p(x)\), then \(P(a \leq X \leq b) = \sum_{x=a}^{b} p(x)\). Similarly, in the continuous case, if the probability density function is \(f(x)\), then we write \(P(a \leq X \leq b) = \sum_{a}^b f(x)dx\).

This holds across other defining identities as well, for instance discussing the expected value or variance of a random variable. It is worth highlighting the two major differences for working with continuous random variables once more. First, while in the discrete case we think predominantly of probabilities being defined on the singletons, with the probability mass function encoding \(p(x) = P(X = x)\), these probabilities are all zero for continuous random variables. We can make this argument more concretely now using our technique for calculating probabilities based on the density function, where \[P(X = a) = P(a \leq X \leq a) = \int_{a}^{a} f(x)dx = 0.\] As a result, no matter the value or the random variable under consideration, we always know that \(P(X = x) = 0\) for continuous quantities.

Secondly, the density function does not directly encode probabilities, and so can take on values greater than \(1\). As a result, when considering the validity of a probability density function we need to consider not the specific values of the density being bounded, but rather the entire range.⁹

Beyond introductory courses and notes, it is quite common to discuss only continuous random variables. In areas where both discrete and continuous random variables are relevant, a common convention is to simply define the integral sign in such a way so as to read it as a summation if a discrete random variable is being used. That is, in reading beyond these notes you may have authors express \(\sum_{x=0}^5 p(x)\) as \(\int_{0}^5 p(x)dx\), where the summation is implied if \(p(x)\) characterizes a discrete distribution. In these notes we will continue separating out integrals and summations explicitly.

9.4.2 \(\int\) Calculating Expected Values for Continuous Random Variables

Using the convention that summations become integrals when moving from discrete to continuous random variables, we can introduce the idea of a continuous expected value.

Definition 9.5 (Expected Value (Mean) of a Continuous Random Variable) For a continuous random variable, \(X\), the expected value is interpreted as the center of mass of the distribution. Supposing that \(X\) has density function, \(f(x)\), then \[E[X] = \int_{-\infty}^\infty xf(x)dx.\] When the random variable \(X\) is defined on a bounded support \(\mathcal{X}\), the expected value can be equivalently written as the integral only over that support \[E[X] = \int_{\mathcal{X}} f(x)dx.\]

Beyond the swapping of the summation for an integral, expected values behave equivalently whether the underlying distribution is discrete or continuous. That is, any of the properties relating to expected values can be written in terms of the expectation notation, \(E[\cdot]\), with the relevant sum or integral being computed as required. The quantities are otherwise interpreted in the same manner as well. Notably, this means that the Law of the Unconscious Statistician holds in the continuous case.

The Law of the Unconscious Statistician

The law of the unconscious statistician (LOTUS) states that, for a random variable \(X\), if we wish to find \(E[g(X)]\), then we compute \[E[g(X)] = \int_{-\infty}^\infty g(x)f_X(x)dx.\]

Using the continuous version of the LOTUS, we can define the following quantities which parallel their discrete counterparts.

Expected Value of a Linear Transformation

If \(a\) and \(b\) are arbitrary real numbers then, \[E[aX + b] = aE[X] + b.\]

Definition 9.6 (Variance) The variance of a random variable, typically denoted \(\text{var}(X)\), is given by the expected value of the squared deviations of a random variable from its mean. That is, \[\text{var}(X) = E\left[(X - E[X])^2\right].\]

Computing the Variance

The variance of a random variable, \(X\), can be computed as \[\text{var}(X) = E[(X - E[X])^2] = E[X^2] - E[X]^2.\]

Variance of a Linear Transformation

If \(a\) and \(b\) are arbitrary real numbers then, \[\text{var}[aX + b] = a^2\text{var}(X).\]

Definition 9.7 (Standard Deviation) The standard deviation of a random variable is the square root of the variance, which is to say \[\text{SD}(X) = \sqrt{\text{var}(X)}.\]

Example 9.6 (Charles and Sadie Potato Yield) Charles and Sadie have purchased a plot of land and they are looking to do some sustainable development of it. In their planning, they are looking at different crops that they could grow. Charles and Sadie decide that potatoes sound particularly fun, and do some research into the amount that they can anticipate from each plant. From their research they find that the probability density function for single plant potato yield (in pounds) is given by \[f(x) = \frac{25}{52}\exp\left(-\frac{25x}{52}\right) \quad x \geq 0.\]

What is the expected yield, in pounds, for a single potato plant?
What is the variance and standard deviation for the yield for a single potato plant?
While Sadie is happy to work in pounds, Charles much prefers kilograms. Moreover, the yield given by the previous distribution function was over counting by \(0.2\)lbs per plant, since they had not considered the dirt that came with the harvest. What is the actual expected value, variance, and standard deviation for the total yield in kilograms (note, \(1\) kilogram is \(2.2\) pounds).

Solution

To get the expected yield we find \[E[X] = \int_{0}^\infty xf(x)dx = \int_{0}^\infty x\frac{25}{52}\exp\left(-\frac{25x}{52}\right)dx.\] This can be solved via integration by parts as \[\begin{align*} E[X] &= \int_{0}^\infty x\frac{25}{52}\exp\left(-\frac{25x}{52}\right)dx \\ &= \left[-x\exp\left(-\frac{25x}{52}\right)\right]_{x=0}^\infty + \int_{0}^\infty \exp\left(-\frac{25x}{52}\right)dx \\ &= 0+\left[-\frac{52}{25}\exp\left(-\frac{25x}{52}\right)\right]_{x=0}^\infty \\ &= \frac{52}{25}. \end{align*}\]
For the variance, we can use the fact that \(\text{var}(X) = E[X^2] - E[X]^2\). Note that \(E[X^2]\) can be computed in much the same way as \(E[X]\), requiring two applications of integration by parts, \[\begin{align*} E[X^2] &= \int_{0}^\infty x^2\frac{25}{52}\exp\left(-\frac{25x}{52}\right)dx \\ &= \left[x^2\exp\left(-\frac{25x}{52}\right)\right]_{x=0}^\infty + 2\int_{0}^\infty x\exp\left(-\frac{25x}{52}\right) \\ &= 2\int_{0}^\infty x\exp\left(-\frac{25x}{52}\right) \\ &= 2\times\frac{52}{25}\times\int_{0}^\infty x\frac{25}{52}\exp\left(-\frac{25x}{52}\right) \\ &= \frac{104}{25}\times E[X] \\ &= \frac{104}{25}\times\frac{52}{25}. \end{align*}\] Thus, \[\text{var}(X) = \frac{104}{25}\times\frac{52}{25} - \left(\frac{52}{25}\right)^2 = \left(\frac{52}{25}\right)^2.\] As a result, \(\text{SD}(X) = E[X] = \frac{52}{25}\).
If \(X\) is the weight in pounds, then the new weight will be \[Y = frac{(X - 0.2)}{2.2} = \frac{1}{2.2}X - \frac{1}{11}.\] Then, we can apply the linear transformation theorems to get \[E[Y] = \frac{1}{2.2}E[X] - \frac{1}{11} = \frac{47}{55}.\] Similarly, we have \[\text{var}(Y) = \frac{1}{2.2^2}\text{var}(X) = \frac{2704}{3025}.\] This leads to a standard deviation of \[\text{SD}(X) = \frac{52}{55}.\]

9.4.3 \(\int\) Calculating Percentiles for Continuous Random Variables

In the same way that expected values generalized from the discrete to the continuous case, so too will percentiles.

Definition 9.8 (Percentiles) The \(100p\)th percentile, is denoted \(\zeta(p)\) and is the value such that \(P(X \leq \zeta(p)) = p\). Thus, the median is given by \(\zeta(0.5)\) and is also called the \(50\)th percentile.

A key distinction between percentiles in discrete case as compared to the continuous case is that, in the discrete case, it was often not possible to find \(\zeta(p)\) such that \(P(X \leq \zeta(p)) = p\) held exactly. Instead, we found \(\zeta(p)\) such that \(P(X \leq \zeta(p)) \geq p\) and \(P(X \geq \zeta(p)) \geq p\). In the continuous case, this is not typically required. This gives two (equivalent) techniques for solving for a given percentile using continuous distributions. If the cumulative distribution function, \(F(x)\), is known then \(\zeta(p) = F^{-1}(p)\).¹⁰

Alternatively, we can work from the density function directly and solve the integral equation, \[\int_{-\infty}^{\zeta(p)} f(x)dx = p,\] for \(\zeta(p)\). Doing so implicitly works out the cumulative distribution function as an intermediate step, however, there are cases where there is no closed-form solution for the cumulative distribution function but this technique can still be used.

Given the definition of a percentile in the continuous case, we can introduce both the median and the interquartile range as being exactly analogous to the quantities in the discrete case.

Definition 9.9 (Median (Continuous)) The median of a distribution is the \(50\)th percentile, \(\zeta(0.5)\). That is, the median \(m\) is the value such that \(P(X \leq m) = 0.5\).

Definition 9.10 (Interquartile Range (IQR)) The interquartile range, or IQR, is defined as \(\zeta(0.75) - \zeta(0.25)\), the difference between the third and first quartiles. It is a measure of spread, and is typically denoted as \(\text{IQR} = Q3 - Q1\), where \(Q\) stands for quartiles.

Example 9.7 (Median Potato Yield) Still interested in the potatoes that they could grow on their land, Charles and Sadie want to further investigate what they should expect for the potatoes that they grow. While they now understand the mean and variance, they figure that it is probably worth understanding the median and interquartile range as well, as this may give a better capacity to plan for the best and worst case scenarios. Suppose that the probability density function for single plant potato yield (in pounds) is given by \[f(x) = \frac{25}{52}\exp\left(-\frac{25x}{52}\right) \quad x \geq 0.\]

What is the median yield for a single potato plant?
What is the interquartile range for the yield of a single potato plant?

Solution

For the median we need to solve \(F(x) = 0.5\) for \(x\). We could do this direct from the integral, or by first finding the cumulative distribution function. We will first find the cumulative distribution function to ease the efforts required for the interquartile range calculation. Note that \[F(x) = \int_{0}^x \frac{25}{52}\exp\left(-\frac{25t}{52}\right)dt = \left[-\exp\left(-\frac{25t}{52}\right)\right]_{t=0}^{x} = 1 - \exp\left(-\frac{25x}{52}\right).\] Then, we get \[\begin{align*} 0.5 &= 1 - \exp\left(-\frac{25x}{52}\right) \\ 0.5 &= \exp\left(-\frac{25x}{52}\right) \\ \log(0.5) &= -\frac{25x}{52} \\ x &= \frac{52}{25}\log(2) \\ &\approx 1.442. \end{align*}\]
The IQR first requires Q1 and Q3. Thus, we solve these in the same way as above. In fact, for general percentile we get \[\begin{align*} p &= 1 - \exp\left(-\frac{25x}{52}\right) \\ 1-p &= \exp\left(-\frac{25x}{52}\right) \\ \log(1-p) &= -\frac{25x}{52} \\ x &= \frac{52}{25}\log(\frac{1}{1-p}). \end{align*}\] Thus, we have \[\text{IQR} = \frac{52}{25}\log(\frac{1}{0.25}) - \frac{52}{25}\log(\frac{1}{0.75}) \approx 2.2851.\]

9.4.4 The Named Continuous Distributions

Just as with discrete distributions, there are named continuous distributions. These are typically governed by either a density function or cumulative distribution function, alongside the expected value and variance. Just like the named discrete distributions, by matching the underlying scenario to the correct process we are able to avoid a lot of work in understanding the behaviour of the random quantities. Now, because calculus is not assumed knowledge, we will not work too widely with continuous random variables. We will introduce several named continuous distributions: the uniform distribution¹¹, the normal distribution,¹² as well as the \(t\), exponential and gamma distributions.¹³

9.5 The Uniform Distribution

The uniform distribution¹⁴ is parameterized over an interval specified as \((a,b)\). On this interval, equal probability density is given to every event, which is to say that the density function is constant. Specifically, if \(X\sim\text{Unif}(a,b)\) then \[f(x) = \begin{cases}\frac{1}{b-a} & x \in (a,b) \\ 0 & \text{otherwise}.\end{cases}\] From the density function we can find that \[F(x) = \frac{x - a}{b - a}\] for \(x \in (a,b)\), with \(F(x) = 0\) for \(x < a\) and \(F(x) = 1\) for \(x > b\). Moreover, we have \(E[X] = \frac{a+b}{2}\) and \(\text{var}(X) = \frac{(b-a)^2}{12}\).

Example 9.8 (Characterizing the Wait Time) Still considering the wait time for buses in the city, Sadie points out that the bus they were waiting for follows a \(\text{Unif}(0,15)\) distribution. They can use their newfound wisdom to make deeper conclusions about the process!¹⁵

How long should they expect to wait for the bus?
What is the variance for the amount of time that they will be waiting?

Solution

Here, we know that \(X\sim\text{Unif}(0,15)\).

\(E[X]\) is \(\dfrac{a+b}{2} = \dfrac{0+15}{2} = 7.5\), so they should expect to wait \(7.5\) minutes.
The variance is \(\text{var}(X) = \dfrac{(15 - 0)^2}{12} = 18.75\).

The uniform distribution is analogous to the discrete uniform. Any time there is an interval of possible outcomes which are all equally likely, the uniform distribution is the distribution to use. Compared with other distributions it is also fairly straightforward to work with, which makes it a useful demonstration of the concepts relating the continuous probability calculations.¹⁶

9.6 The Normal Distribution

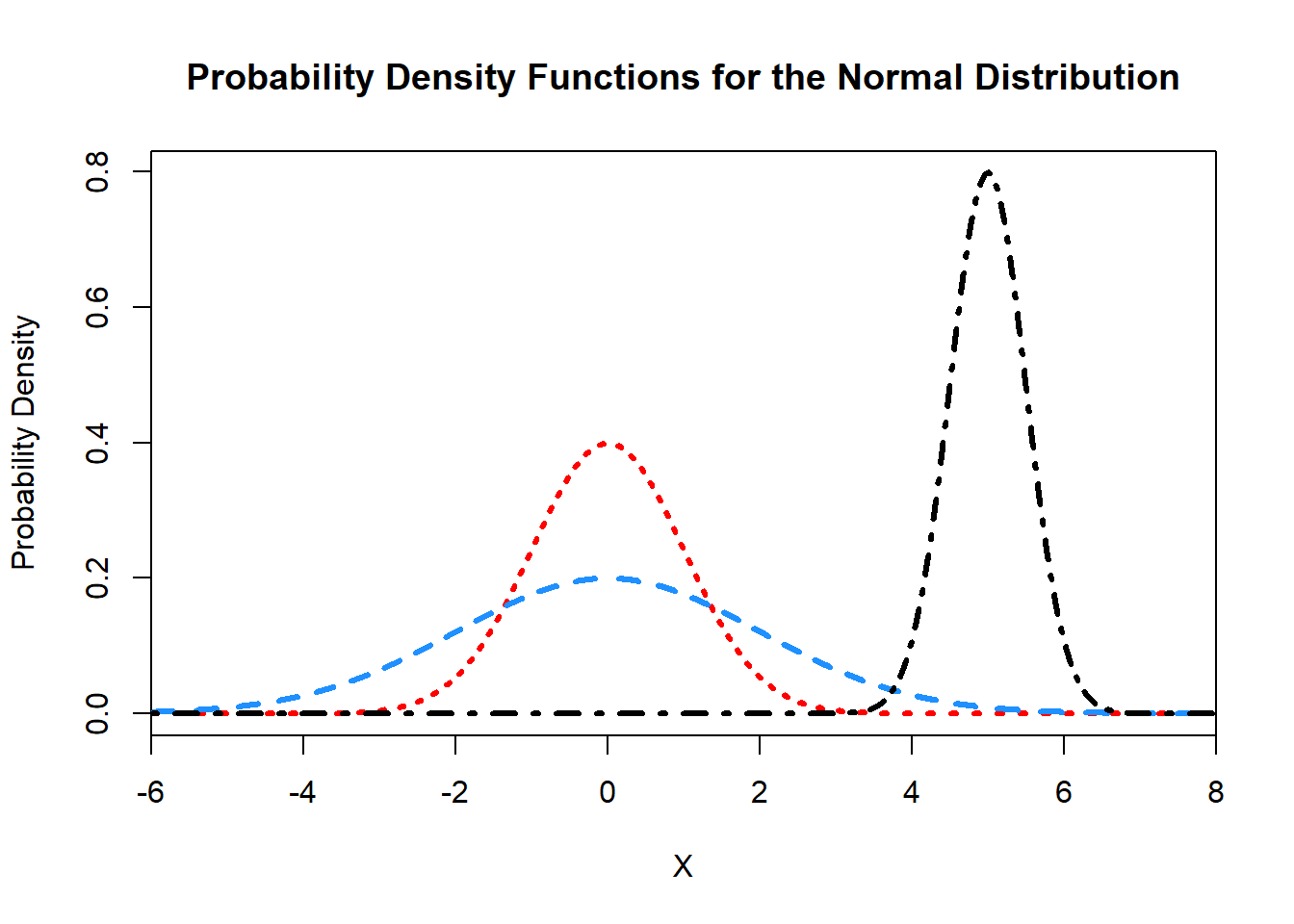
The normal distribution, also sometimes referred to as the Gaussian distribution, is a named continuous distribution function defined on the complete real line. The distribution is far and away the most prominently used distribution in all of probability and statistics. In fact, most people have heard of normal distributions even if they are not aware of this fact. Any time that there is a discussion of a bell curve, for instance, this is in reference to the normal distribution. Normally distributed quantities arise all over the place from measurements of heights, grades, or reaction times through to levels of job satisfaction, reading ability, or blood pressure. There is a tremendous number of normally distributed phenomena naturally occurring in the world, which renders the normal distribution deeply important across a wide range of domains.

Perhaps more important than the places where the normal distribution arises in nature are the places where it arises mathematically. Later in these notes we will see a result, the central limit theorem, which is one of the core results in all of statistics. Much of the statistical theory that drives scientific inquiry sits atop the central limit theorem. And at the core of the central limit theorem is the normal distribution. It is virtually impossible to overstate the importance of the normal distribution, and as a result, it is worthy of investigation.

9.6.1 The Specification of the Distribution

A normal distribution is parameterized by two parameters: the mean, \(\mu\), and the variance \(\sigma^2\). We write \(X\sim N(\mu,\sigma^2)\). These parameters directly correspond to the relevant quantities such that \(E[X] = \mu\) and \(\text{var}(X) = \sigma^2\). The density function is given by \[f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right).\] This can be quite unwieldy to work with, however, when it is plotted we see that the normal distribution takes on a bell curve which is centered at \(\mu\).

Figure 9.2: Three normal distribution densities plotted with mean 0 (red and blue), and mean 5 (black). The red density has variance 1, the blue density has variance 4, and the black density has variance 0.25.

9.6.2 The Standard Normal Distribution

Normally distributed random variables are particularly well-behaved. One way in which this is true is that if you multiply a normally distributed random variable by a constant, it will remain normally distributed, and if you add a constant to a normally distributed random variable, it will remain normally distributed. Consider, for \(X\sim N(\mu,\sigma^2)\), taking the \(X - \mu\). From our discussions of expected values we know that \(E[X-\mu] = E[X]-\mu = 0\). Furthermore, adding or subtracting a constant will not change the variance. Thus, \(X-\mu\sim N(0,\sigma^2)\).

Now, consider dividing this by \(\sigma\), or equivalently, multiply by \(\dfrac{1}{\sigma}\). The expected value of the new quantity will be \(\dfrac{1}{\sigma}\times 0 = 0\), and, from our discussions regarding the variance of linear transformations, the variance of the new quantity will be \(\frac{1}{\sigma^2}\times\sigma^2 = 1\). Taken together then, if \(X\sim N(\mu,\sigma^2)\), \[Z = \frac{X - \mu}{\sigma} \sim N(0,1).\] This holds true for any normal distribution with any mean or variance values. This straightforward transformation allows us to discuss normal distributions in terms of \(N(0,1)\). We call this the standard normal distribution, and will typically use \(Z\) to denote a random variable from the standard normal distribution.

Definition 9.11 (Standard Normal Distribution) The standard normal distribution is the version of the normal distribution with mean \(0\) and variance \(1\). We say that \(Z\) follows a standard normal, and write \(Z\sim N(0,1)\), if the density of \(Z\) is given by \[f_Z(z) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{z^2}{2}\right).\] We denote the density of \(Z\) as \(\varphi(z)\), and the cumulative distribution function of \(Z\) as \(\Phi(z)\). The cumulative distribution function, \(\Phi(z)\), does not have a nice form to be written down, however, it is a commonly applied enough function that many computing languages have implemented it, including of course R.¹⁷

The utility in this process of converting normally distributed random variables to be standard normal random variables, a process known as standardization, is demonstrated by realizing that events can be converted using the same transformations. Specifically, suppose we have \(X \sim N(\mu,\sigma^2)\), and we want to find \(P(X \leq x)\). Note that, \(X \leq x\) must also mean that \[\frac{X-\mu}{\sigma} \leq \frac{x - \mu}{\sigma},\] through an application of the same transformation to both sides. But we know that the left hand side of this inequality is exactly \(Z\), a standard normal random variable with cumulative distribution function \(\Phi(z)\). Thus, \[P(X \leq x) = P\left(Z \leq \frac{x - \mu}{\sigma}\right) = \Phi\left(\frac{x-\mu}{\sigma}\right).\] Using this trick of standardization any normal probability can be converted into a probability regarding the standard normal.

Example 9.9 (Charles and Sadie Explore House Plants) Charles and Sadie learn that the heights of fully grown house plants are often normally distributed. They are exploring which plants will work best in their new apartment, but are finding it difficult to reason about them in comparison to one another. Some plants end up being taller on average with a lot more variability, while others may be shorter but far more certain. Sadie realizes that the cumulative distribution function of a standard normal, \(\Phi(z)\), can be evaluated using their smart phones. As a result, they get to work expressing different probabilities in terms of \(\Phi(z)\).

They are comparing four different plant species. These species have heights according to the following random variables.

Plant \(A\) has height \(X\), which follows a normal distribution with mean \(90\) and variance \(100\).
Plant \(B\) has height \(Y\), which follows a \(N(110, 400)\) distribution.
Plant \(C\) has height \(V\), which follows a normal distribution centered on \(70\) with standard deviation \(7\).
Plant \(D\) has height \(W\), which follows a normal distribution with \(\mu=85\) and \(\sigma^2 = 81\).

Express each of the following probabilities in terms of \(\Phi(z)\), the cumulative distribution function of a standard normal random variable.

One spot the plants cannot be too tall. What is the probability that they can fit plant \(A\) into a spot which cannot accommodate plants taller than \(80\)cm?
A second spot would be strange to have too short of a plant in. If they require the plant to be at least \(125\)cm, what is the probability they can use plant \(B\)?
A third spot can accommodate plants that are either under \(60\)cm if they use a stand, or else over \(90\)cm. How likely is it that plant \(C\) will work in this spot?
A fourth spot requires a plant that is somewhere between \(80\)cm and \(90\)cm. What is the probability that plant \(D\) will work?

Solution

Here we wish to standard a \(N(90, 100)\) random variable. To do this we note that \[\frac{X-90}{\sqrt{100}} = \frac{X - 90}{10} \sim N(0,1).\] Thus, taking \(Z \sim N(0,1)\), we know that \[P(X \leq 80) = P\left(\frac{X - 90}{10} \leq \frac{80 - 90}{10}\right) = P(Z \leq -1) = \Phi(-1).\]
Here we wish to standard a \(N(110, 400)\) random variable. To do this we note that \[\frac{Y-110}{\sqrt{400}} = \frac{Y - 110}{20} \sim N(0,1).\] Thus, taking \(Z \sim N(0,1)\), we know that \[P(Y \geq 125) = P\left(\frac{Y - 110}{20} \geq \frac{125 - 110}{20}\right) = P(Z \geq \frac{3}{4}) = 1 - \Phi(0.75).\]
Here we wish to standard a \(N(70, 49)\) random variable. To do this we note that \[\frac{V-70}{7} \sim N(0,1).\] Thus, taking \(Z \sim N(0,1)\), we know that \[P(V \leq 60) = P\left(\frac{V - 70}{7} \leq \frac{60 - 70}{7}\right) = P(Z \leq -\frac{10}{7}) = \Phi(-\frac{10}{7}).\] Moreover, we know that \[P(V \geq 90) = P\left(\frac{V - 70}{7} \geq \frac{90 - 70}{7}\right) = P(Z \geq \frac{20}{7}) = 1 - \Phi(\frac{20}{7}).\] Thus, the probability this will be acceptable will be \(1 - \Phi(\frac{20}{7}) + \Phi(-\frac{10}{7})\).
Here we wish to standard a \(N(85, 81)\) random variable. To do this we note that \[\frac{W-85}{\sqrt{81}} = \frac{W - 85}{9} \sim N(0,1).\] Thus, taking \(Z \sim N(0,1)\), we know that \[\begin{multline*}P(80 \leq W \leq 90) = P\left(\frac{80 - 85}{9} \leq \frac{W - 85}{9} \leq \frac{90 - 85}{9}\right) \\ = P(Z \leq \frac{5}{9}) - P(Z \leq -\frac{5}{9}) = \Phi(\frac{5}{9}) - \Phi(-\frac{5}{9}).\end{multline*}\]

As a result, combining our knowledge of continuous random variables, with the process of standardization we are able to calculate normal probabilities for any events relating to normally distributed random quantities. Moreover, since the shape of the normal distribution is so predictable, it is often easy to draw out the density function, and indicate on this graphic the probabilities of interest, which in turn helps with the required probability calculations. Calculating probabilities from normal distributions remains a central component of working with statistics and probabilities beyond these notes. Developing the skills and intuition at this point, through repeated practice is a key step in successfully navigating statistics here and beyond.

When you have access to a computer, and your interest is in calculating a normal probability, as described above, there is not typically a need for standardization. However, it remains an important skill for several reasons. First, by always working with the same normal distribution, you will develop a much more refined intuition for the likelihoods of different events. It goes beyond working with the same family of distributions, you get very used to working with exactly the same distribution. Second, you will likely become quite familiar with certain key critical values of the standard normal distribution. These values arise frequently, and allow you to quickly approximate the likelihood of different events. Finally, as we begin to move away from studying probability and into studying statistics, the standard normal will feature prominently there.

9.6.3 The Empirical Rule and Chebyshev’s Inequality

Another way in which the normal distribution is well behaved is summarized in the emprical rule. The shape of the distribution is such that, no matter the specific mean or variance, all members of the family remain quite similar. This enables the derivation of an easy, approximate result, to help intuitively gauge the probabilities of normal events.

The Empirical Rule

The empirical rule is a mathematical result regarding the probability of a normally distributed random variable. If \(X\) has a normal distribution with mean \(\mu\) and variance \(\sigma^2\), then:

The probability of observing a value within \(\sigma\) of the mean is approximately \(0.68\);
The probability of observing a value within \(2\sigma\) of the mean is approximately \(0.95\); and
The probability of observing a value within \(3\sigma\) of the mean is approximately \(0.997\).

In words, the empirical states that almost all of the observations from a normal distribution will fall in the interval \(\mu\pm3\sigma\). In mathematical terms, the empirical rule is summarized as \[\begin{align*} P(\mu-\sigma\leq X \leq \mu + \sigma) &\approx 0.68 \\ P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) &\approx 0.95 \\ P(\mu - 3\sigma \leq X \leq \mu + 3\sigma) &\approx 0.997. \end{align*}\] With the standard normal we can replace \(\mu\) with \(0\), and \(\sigma\) with \(1\) to get a version which is slightly more concise to state. It is then possible to combine these different intervals by recognizing the symmetry in the normal distribution. That is, \(P(\mu \leq X \leq \mu + \sigma) \approx \dfrac{0.68}{2} = 0.34\).

Example 9.10 (Charles and Sadie Can Never Have Enough House Plants) Their standardization efforts paid off, and Charles and Sadie found some plants that should fit the spaces that they need once they’ve grown up. Because of how well the plants worked out, they wanted to buy some more. They end up back at the store, and they know that they need to get a plant that will grow to be between \(70\)cm and \(106\)cm. They have several options for plants again:

A plant with heights \(X\) according to \(N(88, 36)\).
A plant with heights \(Y\) according to \(N(124, 324)\).
A plant with heights \(W\) according to \(N(82, 144)\).

Unfortunately, Charles and Sadie forget their phones at home and so they cannot make direct calculations using \(\Phi(z)\). Can you help them, without using a normal probability calculator, determine which plant has the highest probability of being acceptable?

Solution

Without access to \(\Phi(z)\) we can instead make use of the empirical rule. Consider that for \(X\) we have \(\mu_X = 88\) and \(\sigma = \sqrt{36} = 6\).

If we take the interval \([70, 106]\) then we can consider the terms \[\frac{70-88}{6} = \frac{-18}{6} = -3 \quad\text{and}\quad \frac{106-88}{6} = 3.\] Thus, \(P(70 \leq X \leq 106) = P(\mu_X - 3\sigma_X \leq X \leq \mu_X + 3\sigma_X)\). Using the empirical rule we know that this probability is approximately \(0.997\).
We can approach the same tactics for \(Y\). This time, we get \[\frac{70-124}{\sqrt{324}} = -3 \quad\text{and}\quad \frac{106-124}{18} = -1\]. Thus, \(P(70 \leq Y \leq 106) = P(\mu_Y - 3\sigma_Y \leq Y \leq \mu_Y - \sigma_Y)\). Note that from \(\mu\) to \(\mu-3\sigma\), according the empirical rule, there is \(\dfrac{0.997}{2} = 0.4985\) probability. Similarly, according to the empirical rule there is \(\dfrac{0.68}{2} = 0.34\) probability of being between \(\mu\) and \(\mu-\sigma\). Thus, if we take \(0.4985 - 0.34 = 0.1585\), this gives the probability of being between \(\mu-3\sigma\) and \(\mu-\sigma\), as required.
As above, \[\frac{70-82}{\sqrt{144}} = -1 \quad\text{and}\quad \frac{106-82}{12} = 2\]. As a result, \(P(70 \leq W \leq 106) = P(\mu_W - \sigma_W \leq W \leq \mu_W + 2\sigma_W)\). Note that as in (2) there is \(0.34\) probability of being between \(\mu\) and \(\mu-\sigma\). To be between \(\mu\) and \(\mu + 2\sigma\) there will be probability \(\dfrac{0.95}{2} = 0.475\). As a result, the total probability here will be \(0.34 + 0.475 = 0.815\).

As a result, the first plant has a \(0.997\) chance to fit, the second a \(0.1585\), and the third a \(0.815\) (approximately).

The empirical rule is not exact, and when computing probabilities with access to statistical software it is likely of limited direct utility. However, it is another tool to leverage to continue refining your intuition for the behaviour of random quantities. It is also a good “check” to have, giving an immediate sense of the likelihood of different events. If you compute an answer which seems to contradict the empirical rule, take a second look. If you have someone tell you that they have observed events which are out of line with the empirical rule, be skeptical.

The empirical rule is a useful result to aid in building intuition regarding the normal distribution. However, when quantities are not normally distributed, it does not apply. A related, though somewhat weaker result is Chebyshev’s Inequality. This will hold for any distribution, and can be seen as a useful extension to the empirical rule.

Chebyshev’s Inequality

Chebyshev’s Inequality provides probabilistic bounds on the likelihood of deviating from the mean for any random variable. In words, there is a probability of \(0.75\) or more of observing an observation within two standard deviations, and a probability of at least \(0.8889\) of observing a value within three standard deviations of the mean. Formally, for any \(k > 0\), \[P(\mu - k\sigma \leq X \leq \mu + k\sigma) \geq 1 - \frac{1}{k^2}.\]

Here \(k\) can be any real number which is greater than \(0\). If \(k\leq 1\), this result is uninteresting since the bound simply is \(0\). However, taking \(k=2\) gives the \(0.75\) lower bound outlined above, which is a more useful result. Additionally, there is no requirement for \(k\) to be an integer here, and so, for instance, the probability of observing a value within \(\mu\pm\sqrt{2}\sigma\) is at least \(0.5\), for all distributions.

Example 9.11 (Fitting in the Strange Plants) Charles and Sadie selected a plant to fit in the spot requiring one between \(70\) and \(106\)cm. However, as they are checking out at the store they see a plant that they like much better. They are conflicted since they do not know whether this plant will satisfy normality assumptions in its height. The worker tells them that on average the plant grows to be \(88\)cm, and figures that the variance will be approximately \(51.84\). Charles and Sadie want to be at least \(90\%\) certain that the plant will fit. If they are, they will buy it!

If they assume that the plants heights are normally distributed, should they buy the plant?
If they do not assume that the plants heights are normally distributed, should they buy the plant?

Solution

Note that in this case, we have a mean of \(88\) and a standard deviation of \(7.2\). As a result, we have that \(70\) is \(\mu - 2.5\sigma\) and \(106\) is \(\mu + 2.5\sigma\). The empirical rule does not tell us directly how to address probabilities in this case, however, we know that \[P(X \in [\mu-2\sigma, \mu+2\sigma]) \leq P(X \in [\mu - 2.5\sigma, \mu+2.5\sigma]) \leq P(X \in [\mu-3\sigma,\mu+3\sigma]).\] According to the empirical rule then we can say that, if this plant follows a normal distribution, the probability it is accessible will be between \(0.95\) and \(0.997\). If the normal distribution is a reasonable assumption, then they should buy the plant.
If the distribution is non-normal, then we can instead apply Chebyshev’s inequality. Here we have \(k=2.5\), as solved for in (a). As a result, \[P(\mu - 2.5\sigma \leq X \leq \mu + 2.5\sigma) \geq 1 - \frac{1}{(2.5)^2} = 0.84.\] As a result, if they want to be \(90\%\) certain, without knowing more about the distribution they should not purchase the plant.

9.7 Closure of the Normal Distribution

We have seen a certain type of closure property for the normal distribution when we discussed standardization. That is, adding and multiplying by constants does not change the distribution when working with normally distributed quantities. This is an interesting property which does not hold for most distributions, and makes normally distributed random variables quite nice to work with. The normal distribution has an additional type of closure property which is frequently used.

Suppose that \(X\) and \(Y\) are independent, with \(X\sim N(\mu_X, \sigma_X^2)\), and \(Y\sim N(\mu_Y, \sigma_Y^2)\). In this setting, \[X+Y\sim N(\mu_X+\mu_Y, \sigma_X^2 + \sigma_Y^2).\] That is to say, the addition of two independent normally distributed random variables will also be normally distributed. This extends beyond two in the natural way, simply by applying and reapplying the rule (as many times as is required).

Closure of the Normal Distribution

Suppose that \(X_1, \dots, X_n\) are all independent, with each \(X_i \sim N(\mu_i, \sigma_i^2)\). Then the summation \[\sum_{i=1}^n X_i \sim N(\mu, \sigma^2),\] where \(\mu = \sum_{i=1}^n \mu_i\) and \(\sigma^2 = \sum_{i=1}^n \sigma_i^2\). Notably, if \(X_1,\dots,X_n \stackrel{iid}{\sim} N(\mu,\sigma^2)\), then the summation will be \(N(n\mu, n\sigma^2)\).

If instead of considering the summation, we consider the average of \(n\) independent and identically distributed \(N(\mu,\sigma^2)\) variables, then \[\frac{1}{n}\sum_{i=1}^n X_i \sim N(\mu, \frac{\sigma^2}{n}).\] This follows from an application of our standard expectation and variance transformation rules. This type of result is central to the practice of statistics, and this closure under addition further aids in the utility of the normal distribution.

9.8 Approximations Using the Normal Distribution

A final utility to the normal distribution is in its ability to approximate other distributions. While several of these approximations exist, we will focus on the normal approximation to the binomial as an illustrative example. Historically, these approximations were critical for computing probabilities by hand in a timely fashion. Owing to the widespread use of statistical software, these use cases are more and more limited. However, there are two major advantages to learning these approximations. First, with an approximation it becomes easier to leverage the intuition you will build regarding the normal distribution in order to better understand the behaviour of other random quantities. Second, the normal approximation has the same flavour as many results in statistics, and so it presents an additional path to familiarity with these types of findings.

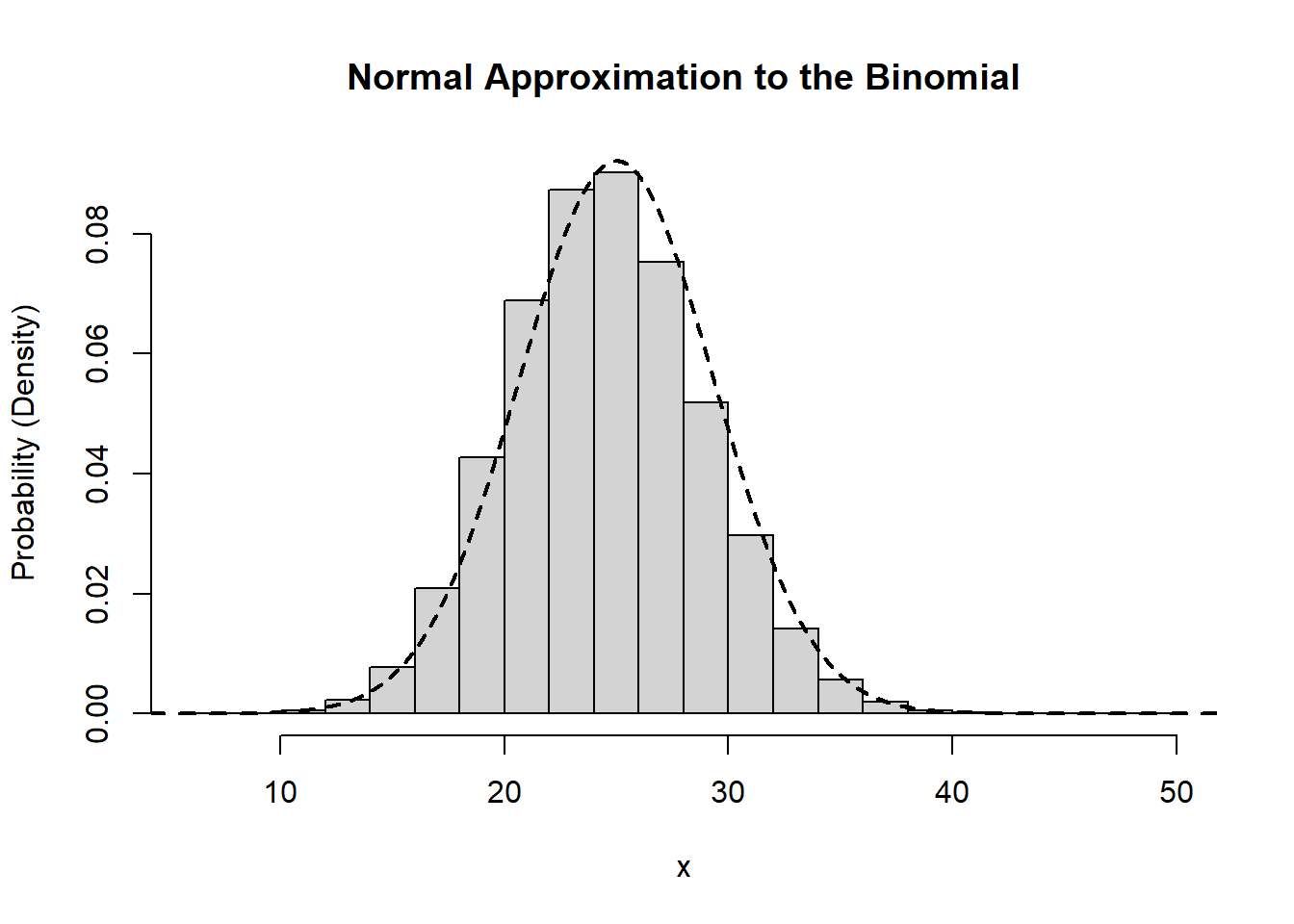
Suppose that \(X\sim\text{Bin}(n,p)\). Through knowledge of the binomial distribution, we know that \(E[X] = np\) and \(\text{var}(X) = np(1-p)\). If \(n\) is sufficiently large then it is possible to approximate a binomial distribution using a normal distribution with the corresponding mean and variance. That is, for \(n\) large enough, we can take \(X\sim\text{Bin}(n,p)\) to have approximately the same distribution as \[W\sim N(np, np(1-p)).\]

Figure 9.3: A plot showing the probability mass function of a \(\text{Bin}(100, 0.25)\) distribution, with a \(N(25, 18.75)\) density overlaid, demonstrating the utility of the approximation.

One consideration that we need to make when applying this approximation has to do with the fact that the normal distribution is continuous while the binomial distribution is discrete. As a result, the normal distribution can take on any value on the real line, where the binomial is limited to the integers. A question that we must answer is what to do with the non-integer valued numbers. The natural solution is to rely on rounding. That is, for any value between \([1.5, 2.5)\) we would round to the nearest integer, which is \(2\).

Definition 9.12 (Continuity Correction) The continuity correction is a technique for adjusting the probabilities computed using a continuous approximation to a discrete random variable. The correction relies on rounding non-integer values, which may be observed with regards to the continuous random variable, to the corresponding integer values for the discrete random variable that is being approximated.

This natural solution is in fact a fairly useful technique, and it is the one that we will make use of in the normal approximation. While rounding is quite natural, the process for leveraging this idea in probability approximation is somewhat backwards. That is, we typically will need to go from probabilities relating to \(X\) and transform those into probabilities relating to \(W\). So, for instance, if we wish to know \(P(X \leq 2)\), then we need to be able to make this a statement regarding the random variable \(W\). In order to do this we need to ask “what is the largest value for \(W\) that would get rounded to \(2\)?” The answer is \(2.5\) and so \(P(X \leq 2) \approx P(W \leq 2.5)\).

A similar adjustment would be required if we instead wanted \(P(X \geq 5)\). Here we would ask “what is the smallest value for \(W\) which would get rounded to \(5\)?” and note that the answer is \(4.5\). Thus, \(P(X \geq 5) \approx P(W \geq 4.5)\). Once we have expressed the probability of interest in terms of the normal random variable, we can use the standard techniques previously outlined to compute the relevant probabilities. It is very important to note that these two results are of the form \(X \geq x\) and \(X \leq x'\). If we instead had considered \(X > x\) or \(X < x'\), we would need to take an additional step.

For continuous random variables whether \(X \geq x\) or \(X > x\) is considered makes no difference. However, for discrete random variables this is not the case. As a result we should first convert the event the an equivalent event which contains the equality sign within the inequality, and then apply the continuity correction. That is, if we want \(P(X > 3)\) first note that for \(X > 3\) to hold, we could equivalently write this as \(X \geq 4\). Alternatively, if the event of interest is \(X < 8\), this is the same as \(X \leq 7\).

Example 9.12 (Charles and Sadie Payouts over a Year) Charles and Sadie are back sitting at the coffee shop, reflecting on all of the probability that they have learned since their games began. They realize that each time they play the game to see who will pay, that is a Bernoulli trial with \(0.5\) probability. As a result, over the course of the year, if they go \(200\) times to get coffee, the number of times each of them will have to pay is governed by a \(\text{Bin}(200, 0.5)\) random variable. Charles realizes that this is infeasible to work with a binomial distribution, and so seeks another way.¹⁸ Sadie suggest that they could use the normal approximation to the binomial.

What is the approximate probability that Charles pays more than \(115\) times in a year, expressed in terms of \(\Phi\).
What is the approximate probability that Sadie will pay between \(86\) and \(107\) times? Explain how this can be approximated numerically.
Give an upper and lower bound that both Charles and Sadie can be \(95\%\) sure they will pay between (that is, two numbers such that the probability they pay at least the lower and at most the upper bound is \(0.95\)).

Solution

For these questions we will take \(X \sim \text{Bin}(200, 0.5)\), and therefore, \(X \dot\sim W \sim N(100, 50)\). Thus, to calculate these probabilities, we can use normal approximations, making sure to apply the continuity corrections.

We want \(P(X > 115)\). This is the same as asking \(P(X \geq 116)\), and with the continuity correction, \(P(X \geq 116) \approx P(W \geq 115.5)\). Thus, we take \[P(W \geq 115.5) = P\left(Z \geq \frac{115.5 - 100}{\sqrt{50}}\right) = 1 - \Phi\left(2.192\right).\] This could be worked out using a normal probability calculator.¹⁹
We want \[P(86 < X < 107) = P(87 \leq X \leq 106 \approx P(87.5 \leq W \leq 106.5).\] Note that if we consider \[\frac{106.5 - 100}{\sqrt{50}} = 0.919 \quad\text{and}\quad \frac{87.5 - 100}{\sqrt{50}} = -1.838.\] If we wanted to get a rough approximation of this, we could say that, from the empirical rule, the probability that \[\begin{multline*}P(\mu_W - 1.838\sigma_W \leq W \leq \mu_W + 0.919\sigma_W) \leq P(\mu_W - 2\sigma_W \leq W \leq \mu_W + \sigma_W) \\ = \frac{0.68}{2} + \frac{0.95}{2} = 0.815.\end{multline*}\] Note that this gives an upper bound on the probability. We could also get a lower bound on the probability by moving in the other directions, \[P(\mu_W - 1.838\sigma_W \leq W \leq \mu_W + 0.919\sigma_W) \leq P(\mu_W - 2\sigma_W \leq W \leq \mu_W) = \frac{0.95}{2} = 0.475.\] This gives a fairly wide range, but we can be relatively confident it will be a lot closer to \(0.815\) than to \(0.475\), since the values are a lot close to \(-2\) and \(1\) than \(-1\) and \(0\).²⁰
Note that, if we use a normal approximation and the empirical rule, we know that there is approximately a \(0.95\) probability that a random variable falls within \(2\sigma\) of the mean. The mean of \(W\) is \(100\) and \(\sigma = \sqrt{50}\), so we can take the interval \([85.8578, 114.1421]\). Note that if we widen this slightly the probability will increase slightly, so that the probability \(W \in [85.5, 114.5]\) must be greater than \(0.95\). The quantity \(P(85.5 \leq W \leq 114.5)\) corresponds to \(P(86 \leq X \leq 114)\), and so we can say that Charles and Sadie can each be roughly \(95\%\) confident that they will need to pay between \(86\) and \(114\) times.²¹

When it is not necessary, it rarely makes sense to use an approximation. There will be cases where the approximation is directly useful, and in those moments it is great to be able to use it. This example of using the normal distribution to approximate a discrete random variable serves as a nice bridge from the study of probability to the study of statistics. In statistics we take a different view of the types of problems we have been considering to date, and we require the tools of probability that have been brought forth. As a result, a deep comfort with manipulating probability expressions is required to build a strong foundation while studying statistics.

9.9 The \(t\) Distribution

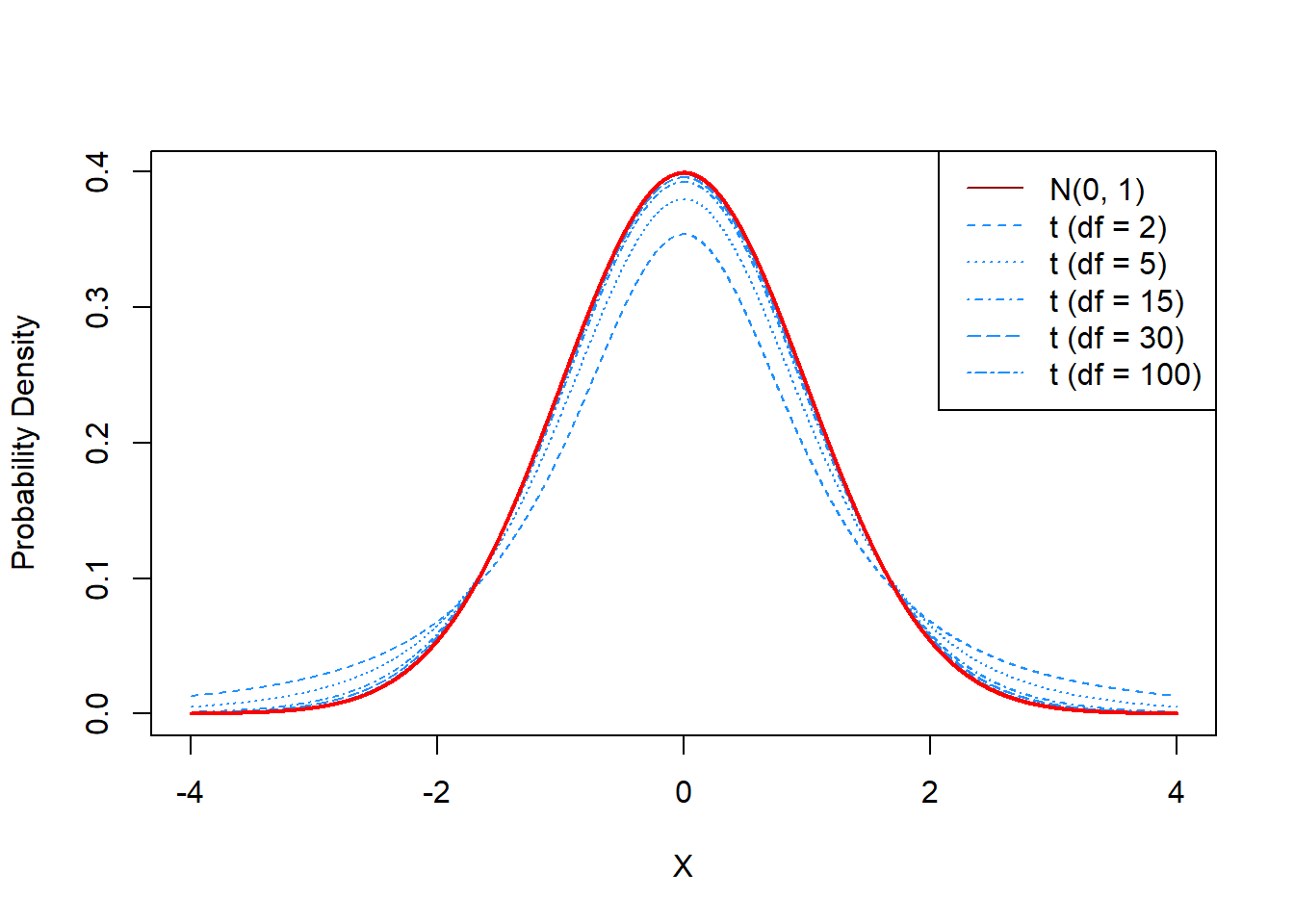
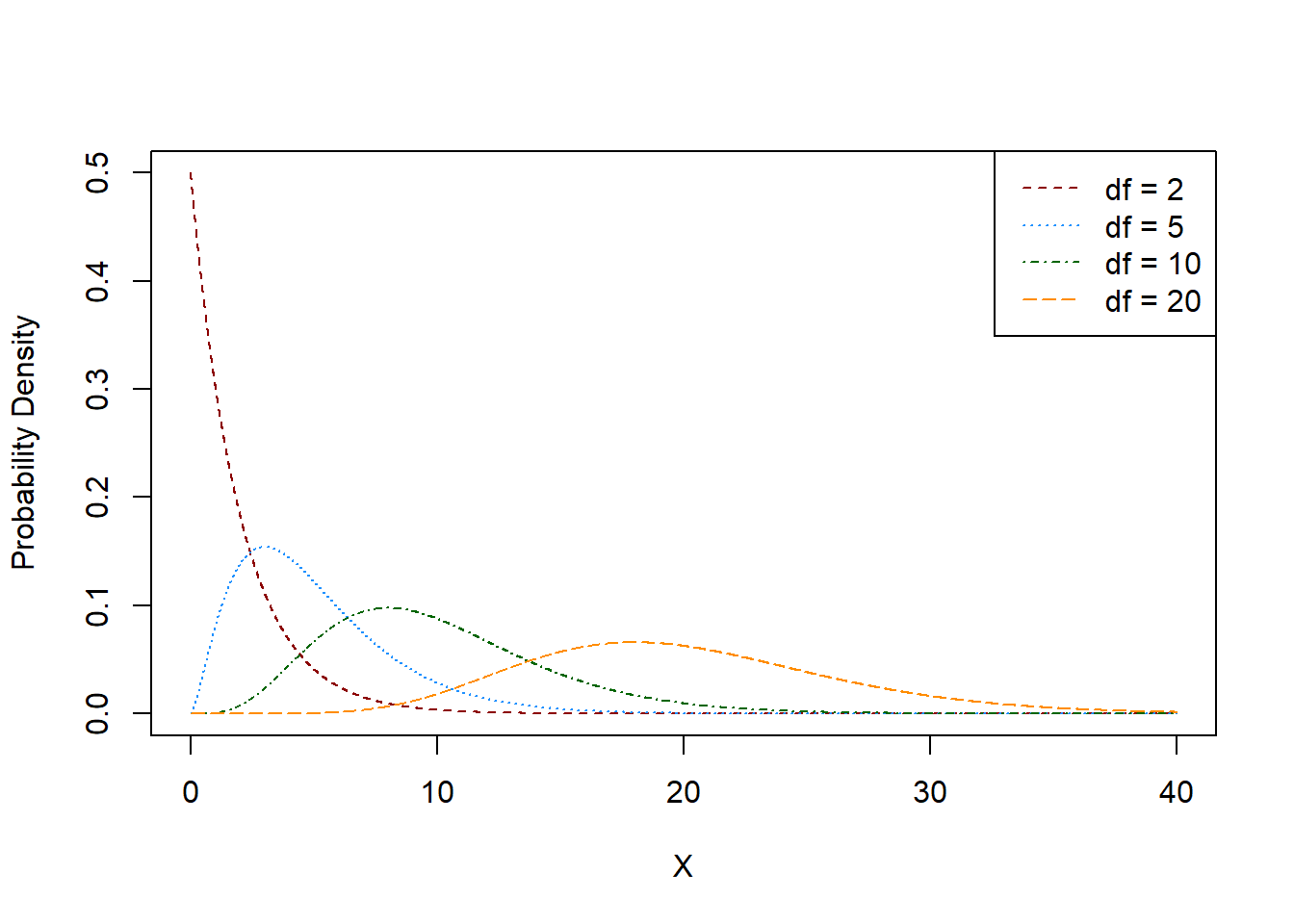
The \(t\) distribution, or Student’s \(t\) distribution named after the individual who popularized the distribution,²² is a bell-shaped distribution, not unlike the normal. It is parameterized by a single parameter, typically denoted \(\nu\) and referred to as the degrees of freedom of the distribution.

While it has a similar shape to the normal distribution, the \(t\) distribution has heavier tails than the normal, which is to say that the probability of observing an extreme event is larger in the \(t\) than in the normal. The \(t\) distribution is always centered at \(0\). Neither the probability density function nor the cumulative distribution function are particularly nice,²³ however, the mean, median, and mode are all \(0\). The variance of the \(t\) distribution is only properly defined for \(\nu > 2\), and in this case if \(X \sim t_{\nu}\) then \[\text{var}(X) = \frac{\nu}{\nu - 2}.\]

The parameter \(\nu\) is any real, positive number. Typically, \(\nu\) is restricted to be a positive integer, for reasons that will become clear later. As \(\nu\) increases, the tails of the \(t\) distribution become smaller and smaller. In the limit, as \(\nu\) tends towards \(\infty\), the \(t\) distribution approaches the standard normal. In fact, when \(\nu \geq 30\), the two distributions are nearly identical.

Figure 9.4: The \(t\) distribution compared with the standard normal. As the degrees of freedom increasing, the density function for the \(t\) becomes closer and closer to the standard normal’s density function, and at \(\nu = \infty\) they theoretically overlap.

Note that, compared with the normal distribution, the \(t\) distributions (particularly with lower degrees of freedom) are more likely to observe extreme events. Based on the empirical rule, we know that the probability of observing an event outside of \(\pm 3\) on the standard normal is \(0.3\%\). This is incredibly rare. By contrast, a \(t\) distribution with \(2\) degrees of freedom has a 9.55% chance of observing a value outside of the interval \(\pm 3\). When it is said that the \(t\) distribution has heavier tails, this is what is meant.

Example 9.13 (Characterizing Scale Errors) Charles and Sadie have been using a new kitchen scale to weigh the vegetables that they have started to grow in their garden. They are trying to keep a detailed log of the counts and weights of all the vegetables that they harvest so that they may know what works and what does not. Unfortunately, they realize that the scale that they are using is not perfectly accurate and seems to be introducing random errors. They begin to investigate these errors.

Suppose that, by repeatedly weighing a reference weight, they determine that the mean error is equal to \(0\) and the variance is equal to \(1\). If the errors are normally distributed, approximately how likely is it that Sadie and Charles observe an error that is greater than \(2\) grams?
Sadie and Charles are skeptical of the normality of the errors. They suspect that perhaps the variance they measured was incorrect, and should have actually been \(2\). If this is the case, what is the corresponding \(t\) distribution that would be valid?
If the errors truly follow the \(t\) distribution from part (b), is it more or less likely that Sadie and Charles will observe an error greater than \(2\) grams, compared with (a)? Explain.

Solution

Given their findings this will follow a \(N(0, 1)\) distribution. By the empirical rule, we know that approximately \(95\%\) of observations will fall within \(\pm 2\) standard deviations of the mean, which in this case is \(1\) gram. Thus, they should observe errors that are smaller than \(2\) in magnitude \(95\%\) of the time, which means the probability of observing an error larger than this is approximately \(0.05\).
If instead they are faced with a \(t\) distribution, if the variance \(2\), then the number of degrees of freedom can be solved for by taking \[2 = \frac{\nu}{\nu - 2} \implies \nu = 4.\] As a result, based on their measured results this would suggest a \(t_4\) distribution.
If the true error distribution is \(t_4\), then it is more likely to observe extreme values since the tails of the \(t\) distribution are heavier than the tails of the normal distribution. Using the computer to estimate this probability gives 0.1161, which is quite a lot larger than the \(0.05\) from (a).

The \(t\) distribution, with its close connections to the normal distribution, will often arise in statistical applications. While less central than the normal, the \(t\) distribution is nevertheless very important for statistical analyses, and will be explored in more depth in the second part of these notes.

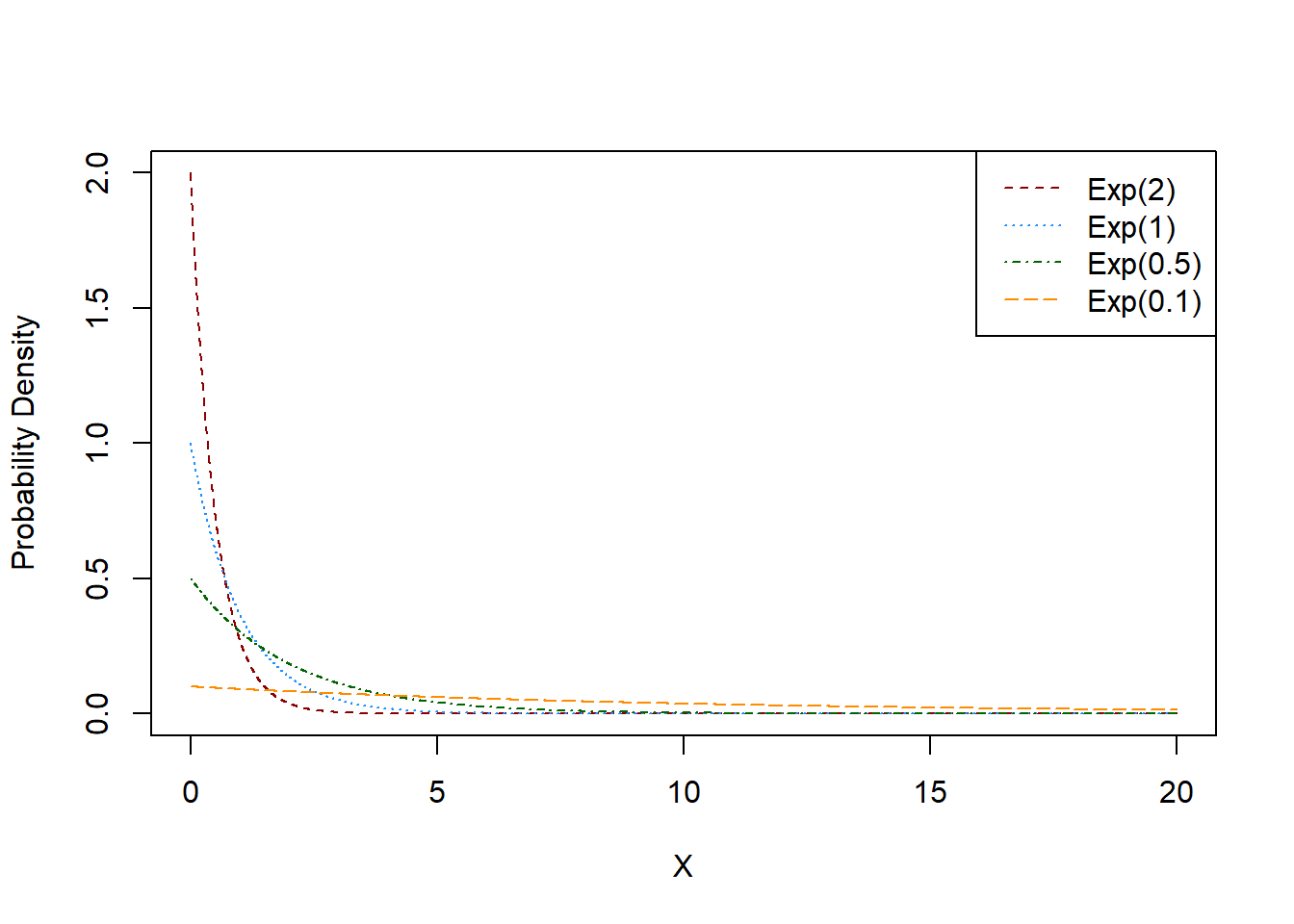
9.10 The Exponential Distribution

The exponential distribution is a single-parameter, skewed distribution that is always positive. The distribution has a probability density functioned supported on \([0,\infty)\), which exhibits exponential decay over this interval, meaning that extreme events are possible, but fairly unlikely. The probability density function is characterized by a single parameter referred to as the rate, and is typically denoted using \(\lambda\). Thus, if \(X \sim \text{Exp}(\lambda)\), then \(X\) is a continuous random variable with probability density function given by \[f(x) = \lambda\exp(-\lambda x), \ x \in [0,\infty).\] The cumulative distribution function for the exponential can be obtained through integration of the density, resulting in \[F(x) = 1 - \exp(-\lambda x).\] Moreover, if \(X \sim \text{Exp}(\lambda)\), then \(E[X] = \dfrac{1}{\lambda}\) and \(\text{var}(X) = \dfrac{1}{\lambda^2}\).²⁴

Figure 9.5: The exponential distribution shown for decreasing values of \(\lambda\). Note that as the rate decreases, the mean increases. As a result, at this resolution, the curve will appear to flatten out. This has the effect of making larger events increasing likely, while decreasing the relative likelihood of small events.

Example 9.14 (Charles and Sadie Install Solar Panels) Charles and Sadie are considering purchasing solar panels for a plot of land they wish to develop. The manufacturer of the solar panels suggests that the panels are exponentially distributed with a mean lifetime of 15 years.

What is the variance in the expected lifetime of these panels?
What is the probability that the panels will need to be replaced in less than \(10\) years?
What is the probability that the panels last at least \(20\) years before needing to be replaced?

Solution

The mean lifespan is \(15\) and so we must have that \(\lambda = \dfrac{1}{15}\). Thus, \(X \sim \text{Exp}(\dfrac{1}{15})\), and \(\text{var}(X) = \dfrac{1}{225}\).
This is \[P(X \leq 10) = F(10) = 1 - \exp(-\dfrac{10}{15}) = 1 - \exp(-2/3) \approx 0.48658.\]
This is \[P(X \geq 20) = 1 - F(20) = 1 - (1 - \exp(-\dfrac{20}{15})) = \exp(-4/3) \approx 0.26360.\]

9.10.1 The Memoryless Property of the Exponential Distribution

The exponential distribution has one particularly important property that makes it a mathematically convenient model, while often challenging its validity for real-world applications. Specifically, the exponential distribution exhibits a memoryless property.²⁵ The memoryless property states, roughly, that if you observe a process that is exponentially distributed before an event has been observed, the remaining time until an event will by exponentially distributed with the same parameter, with the current time being counted as zero. That is, the process seems to not have any memory of the elapsed duration.

The Memoryless Property of an Exponential

Suppose that \(X \sim \text{Exp}(\lambda)\). Then, for any real numbers \(t \geq s \geq 0\), \[P(X \geq t | X \geq s) = P(X \geq t - s).\] In this way, the elapsed time does not impact future probabilities, as the process “forgets”.

Suppose that the lifespan of an electrical component is thought to be exponentially distributed with parameter \(\lambda\). Then, we could work out the probability that the component lasts at least \(10\) years to be \(1 - F(10) = \exp(-10\lambda)\). However, suppose that we knew that the component had already been in service for \(8\) years. Given this information, we can conclude that the probability that the component will last another \(10\) years, is \[P(X \geq 18 | X \geq 8) = P(X \geq 18-8) = P(X \geq 10) = \exp(-10\lambda).\] Thus, if we know the component has been in service for \(10\) years and is still functioning, then it will be equally likely that it will last to \(18\) years as it was to have lasted to \(10\) from the start.

Proof of the Memoryless Property

Note that the memoryless property can be proved using our standard notions of joint and conditional probabilities. Specifically, suppose that \(X \sim \text{Exp}(\lambda)\), and take the event \(A\) to be \(\{ X \geq t \}\) and the event \(B\) to be \(\{X \geq s \}\), for \(t \geq s\). Thus, if \(A\) occurs then we know that \(B\) also occurs, since \(t \geq s\), and as such we have that \(A\cap B = A = \{X \geq t\}\). Thus, \[\begin{align*} P(X \geq t | X \geq s) &= \frac{P(A \cap B)}{P(B)} \\ &= \frac{P(A)}{P(B)} \\ &= \frac{\exp(-t\lambda)}{\exp(-s\lambda)} \\ &= \exp(-(t-s)\lambda) \\ &= P(X \geq t - s). \end{align*}\]

Example 9.15 (Charles and Sadie Consider Used Solar Panels) Charles and Sadie, in doing research on solar panels, are considering going the route of purchasing used solar panels instead of the new ones. The two options in front of them are to go with the new solar panels with a mean lifetime of \(15\) years, or purchase the used panels instead. When they were manufactured, the panels had an anticipated lifespan of \(18\) years, but they have been in service (and are still functioning) for a total of \(12\) years so far.

Which is more likely: that the new solar panels will last \(15\) years or that the used solar panels will last to a total of \(27\) years, given the current status?
Is the exponential distribution likely to be reasonable for this setting? Explain.

Solution

We know that \(P(X \geq 15) = 1 - F(15) = 1 - (1 - \exp(-15/15)) = \exp(-1)\). Thus, there is a probability of approximately \(0.3679\) that the new panels will last for \(15\) years. Using the memoryless property we can work out the probability for the used panels. \[P(X' \geq 27 | X' \geq 12) = P(X' \geq 27-12) = P(X' \geq 15).\] Since the used panels have a mean of \(18\), the rate will be \(\dfrac{1}{18}\), and so the probability is \(\exp(-\dfrac{15}{18}) \approx 0.4346\). Thus, it is more likely that the used panels survive to \(27\) than the new panels surviving to \(15\), given that we have observed the new panels functioning at \(12\) years.
The exponential distribution is likely not appropriate in this case, owing to the memoryless property. Specifically, it seems unlikely that a panel that has been in use for \(15\) years will continue functioning for an additional \(15\) years with the same probability as it was to hit \(15\) years in the first place. We know that as panels are in use, they are likely suffering ongoing deterioration from exposure, just simply through use.

9.10.2 The Exponential Distribution and Poisson Processes

The exponential distribution is closely related to the Poisson distribution through the Poisson process (recall Section 8.7.1 for the definition of the Poisson process). In particular, recall that in a Poisson process we are counting the number of events that occur over a particular interval. We concluded that the number of events, under the assumptions of the Poisson process, that occur during a set interval will follow a particular Poisson distribution. The exponential distribution arises in this context as the distribution for the interarrival times. That is, the number of events that occur during an interval will follow a Poisson distribution, however, the time between any two consecutive events will follow an exponential distribution, with the same rate parameter.

The Interarrival Times for a Poisson Process

Suppose that \(X\) follows a Poisson process with rate \(\alpha\). Then the time between any two successive events will be distributed according to a \(\text{Exp}(\alpha)\) distribution.

Example 9.16 (Sadie’s Vegan Bakery Aspirations: Revisited) Sadie has continued to consider the prospect of opening up a vegan bakery. Market research continues to suggest that it is expected that \(168\) customers would arrive per week, supposing that Sadie’s bakery was open \(8\) hours a day, \(7\) days a week.

How long (in hours) should Sadie expect to wait before the first customer arrives?
How long (in hours) should Sadie expect to wait between the 99th and 100th customer arrivals?
Suppose that Sadie was having a particularly slow start to the day, and it had been \(45\) minutes with no customers. What is the probability Sadie has to wait at least another \(15\) minutes before one finally arrives?

Solution

Customers arrive at a rate of \(3\) per hour, and thus, the time between any customers arriving will be distributed as an \(\text{Exp}(3)\) random variable. As a result, Sadie should expect to wait \(\dfrac{1}{3}\) hours (or \(20\) minutes) for the first customer.
Because all interarrival times are distributed the same way, the time between the \(99\)th and \(100\)th customer is distributed exactly as the time between the \(0\)th and \(1\)st, and as a result, the answer is the same as part (a).
Let \(T\) be the time of arrival for the first customer. We want to know \(P(T > 1 | T > \dfrac{3}{4})\) which we can solve for knowing that \(T \sim \text{Exp}(3)\) and as such the memoryless property applies. Thus, \[P(T > 1 | T > \dfrac{3}{4}) = P(T > \dfrac{1}{4}) = 1 - (1 - \exp(-\dfrac{3}{4})) = \exp(-3/4) \approx 0.4724.\]

9.10.3 The Exponential Distribution in the Real-World

The exponential distribution arises frequently in the modelling of extreme events and in the lifetimes of objects. Most frequently, it arises as the interarrival time in Poisson processes. While it is often not a perfect representation of the underlying reality, it will frequently work well enough to provide useful results. The exponential distribution is itself a part of a large family of distributions know as the gamma distribution. We will consider the Gamma distribution next, however, owing to the compact form and the frequent use of the exponential distribution, it is worth considering separate from the remainder of the gamma family distributions.

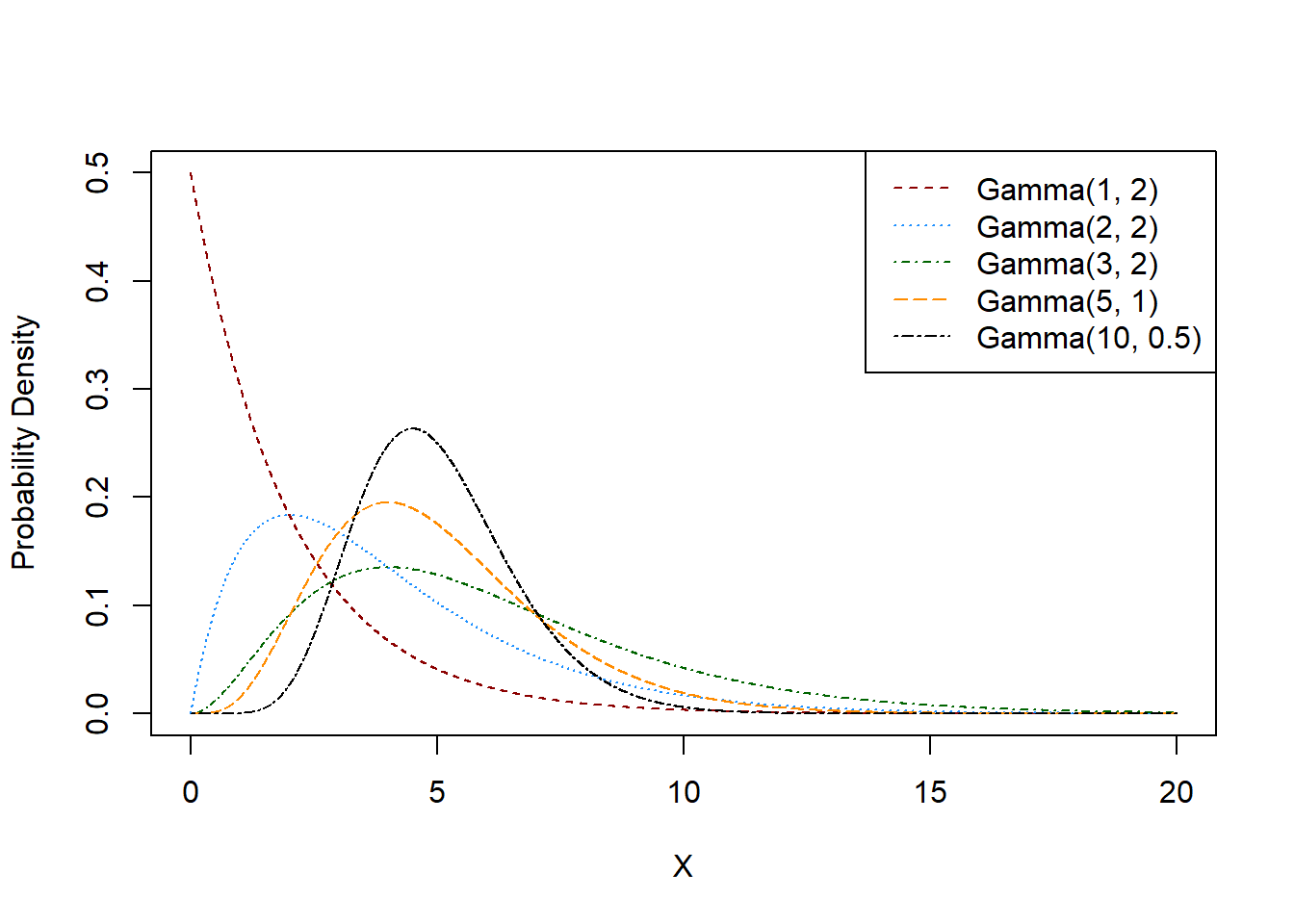
9.11 \(\int\) The Gamma Distribution

The Gamma distribution is a two-parameter distribution, supported on \([0,\infty)\). The distributions parameters are typically denoted \(\alpha\) and \(\beta\) and are referred to as the shape and scale parameter, respectively. The probability density function for \(X \sim \text{Gamma}(\alpha, \beta)\) is given by \[f(x) = \frac{1}{\Gamma(\alpha)\beta^{\alpha}}x^{\alpha - 1}\exp(-\frac{x}{\beta}).\] In this expression, \(\Gamma(\alpha)\) is the Gamma function, a function which is expressible in general only via an integral.

Definition 9.13 (Gamma Function) The Gamma function, denoted \(\Gamma(k)\), is a function given by \[\Gamma(k) = \int_{0}^\infty x^{k-1}e^{-x}dx.\] If \(k\) is a positive integer, then \(\Gamma(k) = (k-1)!\), and in general, \(\Gamma(k) = (k-1)\Gamma(k - 1)\).

Note that if \(X \sim \text{Gamma}(\alpha, \beta)\), then \(E[X] = \alpha\beta\) and \(\text{var}(X) = \alpha\beta^2\).²⁶ The cumulative distribution function can be expressed as \[F(x) = \frac{1}{\Gamma(\alpha)}\gamma(\alpha, \frac{x}{\beta}),\] where \(\gamma(a, b)\) is the lower incomplete gamma function, given by \[\gamma(a, b) = \int_{0}^b x^{a-1}e^{-x}dx.\]

Figure 9.6: The Gamma distribution shown for various combinations of \(\alpha\) and \(\beta\).

9.11.1 Connection to Other Distributions

It was briefly mentioned above that the exponential distribution is actually a special case of the Gamma distribution. If we investigate the corresponding desnity functions we may note that taking \(\alpha = 1\) and \(\beta = \dfrac{1}{\lambda}\) gives us \[f(x) = \lambda\exp(-\lambda x),\] which is exactly the exponential probability density function. As a result we can say that \(\text{Exp}(\lambda) = \text{Gamma}(1, 1/\lambda)\). The Gamma distribution is connected to several important distributions that arise throughout the study of probability and statistics.

Beyond the exponential, the most prominent distribution which is connecte to the Gamma is the chi-squared distribution. The chi-squared distribution is a distribution that arises in many statistical inference procedures. It is characterized by a single parameter, \(\nu\), referred to as the degrees of freedom. To characterize the chi-squared distribution with \(\nu\) degrees of freedom, denoted \(\chi^2_\nu\), we take \(X \sim \text{Gamma}(\nu/2, 2)\). Thus, the mean of the distribution is \(\nu\) and the variance is \(2\nu\).

Figure 9.7: The chi-sqaured distribution shown for increasing degrees of freedom.

9.12 Continuous Probability Calculations in R

Just as with the named discrete distributions, R provides functions for calculating probabilities related to continuous random variables. The relevant functions are, as in the discrete case, d{distname} and p{distname}, where {distname} is one the named distributions. These evaluate the density and cumulative distribution functions, respectively. So for instance, dnorm and pnorm calculate normal probabilities, dt and pt calculate probability for the \(t\) distribution, dexp and pexp calculate exponential probabilities, dgamma and pgamma calculate Gamma probabilities, and dchisq and pchisq calculate the chi-squared probabilities.

Each function takes in a set of parameters to indicate which of the specific distributions is being considered. Note, it is important to ensure that the correct parameterizations are used. For the normal, the functions can take arguments for the mean and standard deviation²⁷ of the normal. If not provided, it will default to the standard normal. The \(t\) and chi-squared distributions each take a degrees of freedom argument, named df. For the exponential, the parameter is named rate. The Gamma distribution can be parameterized either as the shape/scale, or the shape/rate characterization, where we learned the former.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 9.1

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 12}{29}, \quad x \in [-12, 17].\]

What is \(P(X > -4.4)\)?
What is \(P(3.23 \leq X \leq 10.03)\)?
What is \(P(X = 12.73)\)?
What is \(P(X \geq 52)\)?

Question ID: 0559282069

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 9)^2}{256}, \quad x \in [9, 25].\]

What is \(P(X > 22.62)\)?
What is \(P(14.77 \leq X \leq 14.99)\)?
What is \(P(X = 11.5)\)?
What is \(P(X \geq 51)\)?

Question ID: 0008624060

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 3)^2}{400}, \quad x \in [3, 23].\]

What is \(P(X > 22.04)\)?
What is \(P(12.27 \leq X \leq 21.6)\)?
What is \(P(X = 16.01)\)?
What is \(P(X \geq -96)\)?

Question ID: 0656705088

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 16)^2}{16}, \quad x \in [16, 20].\]

What is \(P(X > 16.78)\)?
What is \(P(18.13 \leq X \leq 19.1)\)?
What is \(P(X = 17.11)\)?
What is \(P(X \leq 30)\)?

Question ID: 0010667899

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 4)^2}{324}, \quad x \in [4, 22].\]

What is \(P(X > 8.24)\)?
What is \(P(13.87 \leq X \leq 20.22)\)?
What is \(P(X = 9.34)\)?
What is \(P(X \leq -6)\)?

Question ID: 0111280079

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-1.08x\right),\quad x \in (0,\infty).\]

What is \(P(X > 2.32)\)?
What is \(P(1.44 \leq X \leq 2.46)\)?
What is \(P(X = 70.89)\)?
What is \(P(X \geq -24)\)?

Question ID: 0463825580

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 4}{6}, \quad x \in [-4, 2].\]

What is \(P(X > 1.19)\)?
What is \(P(-0.24 \leq X \leq 1.3)\)?
What is \(P(X = 0.68)\)?
What is \(P(X \leq 62)\)?

Question ID: 0599188925

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 1)^2}{16}, \quad x \in [1, 5].\]

What is \(P(X > 3.1)\)?
What is \(P(3.57 \leq X \leq 3.88)\)?
What is \(P(X = 4.77)\)?
What is \(P(X \leq -13)\)?

Question ID: 0905502594

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-11.9x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.24)\)?
What is \(P(0.1 \leq X \leq 0.21)\)?
What is \(P(X = 7.48)\)?
What is \(P(X \leq -53)\)?

Question ID: 0088332389

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 19}{26}, \quad x \in [-19, 7].\]

What is \(P(X > -4.03)\)?
What is \(P(-13.43 \leq X \leq -8.31)\)?
What is \(P(X = -14.26)\)?
What is \(P(X \geq -33)\)?

Question ID: 0335533933

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{73}{x}\right)^{1.63}, \quad x \in [73, \infty).\]

What is \(P(X > 106.49)\)?
What is \(P(195.67 \leq X \leq 266.41)\)?
What is \(P(X = 1.726229\times 10^{4})\)?
What is \(P(X \geq 16)\)?

Question ID: 0421247229

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-1.88x\right),\quad x \in (0,\infty).\]

What is \(P(X > 1.34)\)?
What is \(P(0.5 \leq X \leq 0.66)\)?
What is \(P(X = 13.55)\)?
What is \(P(X \leq -72)\)?

Question ID: 0409226968

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 17)^2}{169}, \quad x \in [17, 30].\]

What is \(P(X > 28.04)\)?
What is \(P(20.67 \leq X \leq 22.59)\)?
What is \(P(X = 20.72)\)?
What is \(P(X \geq -53)\)?

Question ID: 0360881262

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{79}{x}\right)^{4.24}, \quad x \in [79, \infty).\]

What is \(P(X > 146.81)\)?
What is \(P(123.12 \leq X \leq 139.02)\)?
What is \(P(X = 1722.86)\)?
What is \(P(X \geq 68)\)?

Question ID: 0282279316

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 30}{40}, \quad x \in [-30, 10].\]

What is \(P(X > -1.68)\)?
What is \(P(-0.95 \leq X \leq 5.73)\)?
What is \(P(X = -13.1)\)?
What is \(P(X \leq -74)\)?

Question ID: 0641807344

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{60}{x}\right)^{8.1}, \quad x \in [60, \infty).\]

What is \(P(X > 69.36)\)?
What is \(P(69.02 \leq X \leq 84.43)\)?
What is \(P(X = 1763.21)\)?
What is \(P(X \geq 37)\)?

Question ID: 0200825716

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{25}{x}\right)^{6.21}, \quad x \in [25, \infty).\]

What is \(P(X > 29.96)\)?
What is \(P(29.73 \leq X \leq 30.97)\)?
What is \(P(X = 2476.54)\)?
What is \(P(X \leq -61)\)?

Question ID: 0190565332

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 15)^2}{36}, \quad x \in [15, 21].\]

What is \(P(X > 15.63)\)?
What is \(P(17.24 \leq X \leq 18.5)\)?
What is \(P(X = 15.26)\)?
What is \(P(X \geq 43)\)?

Question ID: 0411438003

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 10)^2}{9}, \quad x \in [10, 13].\]

What is \(P(X > 10.67)\)?
What is \(P(11.8 \leq X \leq 12.47)\)?
What is \(P(X = 10.15)\)?
What is \(P(X \geq 48)\)?

Question ID: 0366079325

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-16.73x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.09)\)?
What is \(P(0.09 \leq X \leq 0.1)\)?
What is \(P(X = 2.63)\)?
What is \(P(X \leq -27)\)?

Question ID: 0732223748

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 4)^2}{100}, \quad x \in [4, 14].\]

What is \(P(X > 9.74)\)?
What is \(P(10.64 \leq X \leq 11.18)\)?
What is \(P(X = 4.32)\)?
What is \(P(X \geq 33)\)?

Question ID: 0415044518

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-4.08x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.25)\)?
What is \(P(0.31 \leq X \leq 0.64)\)?
What is \(P(X = 22.32)\)?
What is \(P(X \geq -77)\)?

Question ID: 0486028828

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{99}{x}\right)^{2.81}, \quad x \in [99, \infty).\]

What is \(P(X > 275.99)\)?
What is \(P(144.97 \leq X \leq 268.81)\)?
What is \(P(X = 5622.89)\)?
What is \(P(X \leq 24)\)?

Question ID: 0045047766

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 24}{38}, \quad x \in [-24, 14].\]

What is \(P(X > 11.08)\)?
What is \(P(-16.1 \leq X \leq -1.49)\)?
What is \(P(X = 5.97)\)?
What is \(P(X \leq 59)\)?

Question ID: 0507752628

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{25}{x}\right)^{2.92}, \quad x \in [25, \infty).\]

What is \(P(X > 46.49)\)?
What is \(P(53.44 \leq X \leq 59.11)\)?
What is \(P(X = 2674.69)\)?
What is \(P(X \geq -33)\)?

Question ID: 0002428235

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 23}{30}, \quad x \in [-23, 7].\]

What is \(P(X > -5.46)\)?
What is \(P(-17.84 \leq X \leq -6.02)\)?
What is \(P(X = -9.02)\)?
What is \(P(X \leq -53)\)?

Question ID: 0309644160

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-18.19x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.07)\)?
What is \(P(0.09 \leq X \leq 0.16)\)?
What is \(P(X = 3.86)\)?
What is \(P(X \geq -90)\)?

Question ID: 0551262246

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 7}{11}, \quad x \in [-7, 4].\]

What is \(P(X > -3.86)\)?
What is \(P(-4.63 \leq X \leq -1.46)\)?
What is \(P(X = -0.05)\)?
What is \(P(X \leq -82)\)?

Question ID: 0270748397

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-9.89x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.28)\)?
What is \(P(0.19 \leq X \leq 0.23)\)?
What is \(P(X = 9.41)\)?
What is \(P(X \geq -84)\)?

Question ID: 0118162236

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{13}{x}\right)^{8.43}, \quad x \in [13, \infty).\]

What is \(P(X > 15.91)\)?
What is \(P(14.94 \leq X \leq 17.56)\)?
What is \(P(X = 327.69)\)?
What is \(P(X \leq -33)\)?

Question ID: 0182305286

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 26}{42}, \quad x \in [-26, 16].\]

What is \(P(X > -24.36)\)?
What is \(P(-18.86 \leq X \leq 6.59)\)?
What is \(P(X = -9.08)\)?
What is \(P(X \leq -80)\)?

Question ID: 0850757073

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 25}{42}, \quad x \in [-25, 17].\]

What is \(P(X > 2.99)\)?
What is \(P(2.64 \leq X \leq 4.28)\)?
What is \(P(X = -5.55)\)?
What is \(P(X \leq 46)\)?

Question ID: 0702783359

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 20)^2}{1}, \quad x \in [20, 21].\]

What is \(P(X > 20.02)\)?
What is \(P(20.53 \leq X \leq 20.82)\)?
What is \(P(X = 20.42)\)?
What is \(P(X \geq -12)\)?

Question ID: 0215081818

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 1}{10}, \quad x \in [-1, 9].\]

What is \(P(X > 2.15)\)?
What is \(P(4.09 \leq X \leq 4.97)\)?
What is \(P(X = 0.59)\)?
What is \(P(X \geq 57)\)?

Question ID: 0476946209

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{44}{x}\right)^{7.04}, \quad x \in [44, \infty).\]

What is \(P(X > 46.54)\)?
What is \(P(61.95 \leq X \leq 65.3)\)?
What is \(P(X = 1649.08)\)?
What is \(P(X \geq 6)\)?

Question ID: 0494268482

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{68}{x}\right)^{3.87}, \quad x \in [68, \infty).\]

What is \(P(X > 97.58)\)?
What is \(P(100.86 \leq X \leq 145.09)\)?
What is \(P(X = 6248.6)\)?
What is \(P(X \geq 61)\)?

Question ID: 0208003512

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 21}{30}, \quad x \in [-21, 9].\]

What is \(P(X > -18.85)\)?
What is \(P(-8.69 \leq X \leq -6.79)\)?
What is \(P(X = -17.01)\)?
What is \(P(X \geq 11)\)?

Question ID: 0389962861

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{77}{x}\right)^{6.83}, \quad x \in [77, \infty).\]

What is \(P(X > 92.38)\)?
What is \(P(101.69 \leq X \leq 109.82)\)?
What is \(P(X = 414.9)\)?
What is \(P(X \geq 43)\)?

Question ID: 0923827960

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-1.05x\right),\quad x \in (0,\infty).\]

What is \(P(X > 1.39)\)?
What is \(P(0.8 \leq X \leq 1.14)\)?
What is \(P(X = 3.63)\)?
What is \(P(X \leq -2)\)?

Question ID: 0852119266

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 4}{10}, \quad x \in [-4, 6].\]

What is \(P(X > 4.64)\)?
What is \(P(1.77 \leq X \leq 2.9)\)?
What is \(P(X = 2.22)\)?
What is \(P(X \leq -90)\)?

Question ID: 0437149118

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 13}{25}, \quad x \in [-13, 12].\]

What is \(P(X > -1.58)\)?
What is \(P(-10.74 \leq X \leq 1.35)\)?
What is \(P(X = -9.88)\)?
What is \(P(X \geq -72)\)?

Question ID: 0641358865

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{82}{x}\right)^{9.58}, \quad x \in [82, \infty).\]

What is \(P(X > 97.24)\)?
What is \(P(82.64 \leq X \leq 89.17)\)?
What is \(P(X = 966.51)\)?
What is \(P(X \geq 19)\)?

Question ID: 0062220231

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 3)^2}{484}, \quad x \in [3, 25].\]

What is \(P(X > 4.76)\)?
What is \(P(12.27 \leq X \leq 13.66)\)?
What is \(P(X = 23.41)\)?
What is \(P(X \geq -25)\)?

Question ID: 0034561761

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-13.36x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.08)\)?
What is \(P(0.02 \leq X \leq 0.08)\)?
What is \(P(X = 0.19)\)?
What is \(P(X \leq -74)\)?

Question ID: 0274299685

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{(x - 2)^2}{576}, \quad x \in [2, 26].\]

What is \(P(X > 24.52)\)?
What is \(P(7.86 \leq X \leq 17.02)\)?
What is \(P(X = 12.86)\)?
What is \(P(X \geq -33)\)?

Question ID: 0574241875

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-16.87x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.13)\)?
What is \(P(0.12 \leq X \leq 0.13)\)?
What is \(P(X = 4.2)\)?
What is \(P(X \geq -55)\)?

Question ID: 0806820397

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = \frac{x + 11}{26}, \quad x \in [-11, 15].\]

What is \(P(X > 0.62)\)?
What is \(P(-4.37 \leq X \leq 10.92)\)?
What is \(P(X = -2.57)\)?
What is \(P(X \geq 98)\)?

Question ID: 0880575605

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{19}{x}\right)^{6.6}, \quad x \in [19, \infty).\]

What is \(P(X > 20.71)\)?
What is \(P(21.51 \leq X \leq 28.99)\)?
What is \(P(X = 1138.79)\)?
What is \(P(X \leq -17)\)?

Question ID: 0720401102

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \exp\left(-13.33x\right),\quad x \in (0,\infty).\]

What is \(P(X > 0.01)\)?
What is \(P(0.16 \leq X \leq 0.21)\)?
What is \(P(X = 1.32)\)?
What is \(P(X \geq -81)\)?

Question ID: 0405566463

Suppose that the cumulative distribution function of \(X\) is given by \[F_X(x) = 1 - \left(\frac{82}{x}\right)^{4.58}, \quad x \in [82, \infty).\]

What is \(P(X > 124.15)\)?
What is \(P(132.79 \leq X \leq 151.74)\)?
What is \(P(X = 1207.48)\)?
What is \(P(X \leq -14)\)?

Question ID: 0674621100

Self Assessment 9.2

Suppose that lifespans of tortoises is normally distributed with a mean of 98 and a variance of 225, and is denoted as \(X\).

What is the probability that a tortoise lives between 74.29 and 128.51 years?
What is the probability that a tortoise lives less than 133.35 years?
What is the probability that a tortoise lives more than 89.15 years?
Approximate the probability that \(X \leq 143\), using the empirical rule.
Approximate the probability that \(98 \leq X \leq 113\), using the empirical rule.

Question ID: 0173086053

Suppose that heights of students in a class is normally distributed with a mean of 95 and a variance of 64, and is denoted as \(X\).

What is the probability that a student is between 87.39 and 112.79 inches tall?
What is the probability that a student is less than 110.1 inches tall?
What is the probability that a student is more than 71.2 inches tall?
Approximate the probability that \(X \leq 87\), using the empirical rule.
Approximate the probability that \(87 \leq X \leq 111\), using the empirical rule.

Question ID: 0401791345

Suppose that heights of students in a class is normally distributed with a mean of 95 and a variance of 36, and is denoted as \(X\).

What is the probability that a student is between 88.26 and 100.22 inches tall?
What is the probability that a student is less than 111.73 inches tall?
What is the probability that a student is more than 92.33 inches tall?
Approximate the probability that \(X \leq 77\), using the empirical rule.
Approximate the probability that \(77 \leq X \leq 83\), using the empirical rule.

Question ID: 0267030643

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 184 and a variance of 324, and is denoted as \(X\).

What is the probability that the apple weighs between 173.59 and 195.14 grams?
What is the probability that the apple weighs less than 224.84 grams?
What is the probability that the apple weighs more than 156.43 grams?
Approximate the probability that \(X \leq 220\), using the empirical rule.
Approximate the probability that \(148 \leq X \leq 238\), using the empirical rule.

Question ID: 0434646840

Suppose that heights of students in a class is normally distributed with a mean of 79 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 76.28 and 85.45 inches tall?
What is the probability that a student is less than 80.63 inches tall?
What is the probability that a student is more than 74.99 inches tall?
Approximate the probability that \(X \leq 79\), using the empirical rule.
Approximate the probability that \(79 \leq X \leq 87\), using the empirical rule.

Question ID: 0718195761

Suppose that lifespans of tortoises is normally distributed with a mean of 113 and a variance of 225, and is denoted as \(X\).

What is the probability that a tortoise lives between 81.7 and 117.67 years?
What is the probability that a tortoise lives less than 146.41 years?
What is the probability that a tortoise lives more than 70.73 years?
Approximate the probability that \(X \geq 83\), using the empirical rule.
Approximate the probability that \(98 \leq X \leq 143\), using the empirical rule.

Question ID: 0668047410

Suppose that lifespans of tortoises is normally distributed with a mean of 120 and a variance of 64, and is denoted as \(X\).

What is the probability that a tortoise lives between 108.02 and 134.25 years?
What is the probability that a tortoise lives less than 129.18 years?
What is the probability that a tortoise lives more than 101.7 years?
Approximate the probability that \(X \geq 120\), using the empirical rule.
Approximate the probability that \(96 \leq X \leq 104\), using the empirical rule.

Question ID: 0534892081

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 2976 and a variance of 434281, and is denoted as \(X\).

What is the probability that an employee earns between 2816.66 and 3901.85 per month?
What is the probability that an employee earns less than 3306.61 per month?
What is the probability that an employee earns more than 1573.38 per month?
Approximate the probability that \(X \geq 4953\), using the empirical rule.
Approximate the probability that \(2317 \leq X \leq 2976\), using the empirical rule.

Question ID: 0870521544

Suppose that heights of students in a class is normally distributed with a mean of 82 and a variance of 9, and is denoted as \(X\).

What is the probability that a student is between 79.18 and 87.26 inches tall?
What is the probability that a student is less than 81.66 inches tall?
What is the probability that a student is more than 73.78 inches tall?
Approximate the probability that \(X \geq 85\), using the empirical rule.
Approximate the probability that \(73 \leq X \leq 76\), using the empirical rule.

Question ID: 0595955760

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 2588 and a variance of 480249, and is denoted as \(X\).

What is the probability that an employee earns between 1346.97 and 4090.26 per month?
What is the probability that an employee earns less than 2570.63 per month?
What is the probability that an employee earns more than 941.43 per month?
Approximate the probability that \(X \geq 3974\), using the empirical rule.
Approximate the probability that \(2588 \leq X \leq 4667\), using the empirical rule.

Question ID: 0091934752

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 906 and a variance of 4900, and is denoted as \(X\).

What is the probability that the bulb lasts between 760.38 and 986.61 hours?
What is the probability that the bulb lasts less than 990.45 hours?
What is the probability that the bulb lasts more than 812.43 hours?
Approximate the probability that \(X \leq 696\), using the empirical rule.
Approximate the probability that \(696 \leq X \leq 766\), using the empirical rule.

Question ID: 0590630894

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 137 and a variance of 441, and is denoted as \(X\).

What is the probability that the apple weighs between 135.3 and 140.03 grams?
What is the probability that the apple weighs less than 155.35 grams?
What is the probability that the apple weighs more than 137.93 grams?
Approximate the probability that \(X \geq 116\), using the empirical rule.
Approximate the probability that \(137 \leq X \leq 200\), using the empirical rule.

Question ID: 0303351515

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 970 and a variance of 4489, and is denoted as \(X\).

What is the probability that the bulb lasts between 969.42 and 979.05 hours?
What is the probability that the bulb lasts less than 987.91 hours?
What is the probability that the bulb lasts more than 920.05 hours?
Approximate the probability that \(X \geq 769\), using the empirical rule.
Approximate the probability that \(769 \leq X \leq 1171\), using the empirical rule.

Question ID: 0642870191

Suppose that heights of students in a class is normally distributed with a mean of 92 and a variance of 36, and is denoted as \(X\).

What is the probability that a student is between 82.83 and 94.25 inches tall?
What is the probability that a student is less than 96.49 inches tall?
What is the probability that a student is more than 83.8 inches tall?
Approximate the probability that \(X \geq 80\), using the empirical rule.
Approximate the probability that \(80 \leq X \leq 98\), using the empirical rule.

Question ID: 0881478041

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 3231 and a variance of 291600, and is denoted as \(X\).

What is the probability that an employee earns between 2769.87 and 3671.61 per month?
What is the probability that an employee earns less than 4000.46 per month?
What is the probability that an employee earns more than 3445.23 per month?
Approximate the probability that \(X \leq 2691\), using the empirical rule.
Approximate the probability that \(1611 \leq X \leq 4311\), using the empirical rule.

Question ID: 0705120144

Suppose that heights of students in a class is normally distributed with a mean of 60 and a variance of 25, and is denoted as \(X\).

What is the probability that a student is between 56.05 and 61.81 inches tall?
What is the probability that a student is less than 71.69 inches tall?
What is the probability that a student is more than 51.01 inches tall?
Approximate the probability that \(X \geq 55\), using the empirical rule.
Approximate the probability that \(50 \leq X \leq 65\), using the empirical rule.

Question ID: 0211965364

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 128 and a variance of 361, and is denoted as \(X\).

What is the probability that the apple weighs between 91.67 and 172.37 grams?
What is the probability that the apple weighs less than 148.49 grams?
What is the probability that the apple weighs more than 95.02 grams?
Approximate the probability that \(X \geq 147\), using the empirical rule.
Approximate the probability that \(90 \leq X \leq 128\), using the empirical rule.

Question ID: 0172819349

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1038 and a variance of 3481, and is denoted as \(X\).

What is the probability that the bulb lasts between 967.78 and 1060.08 hours?
What is the probability that the bulb lasts less than 1091.23 hours?
What is the probability that the bulb lasts more than 887.85 hours?
Approximate the probability that \(X \geq 979\), using the empirical rule.
Approximate the probability that \(979 \leq X \leq 1215\), using the empirical rule.

Question ID: 0854206092

Suppose that heights of students in a class is normally distributed with a mean of 80 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 75.26 and 86.3 inches tall?
What is the probability that a student is less than 83.35 inches tall?
What is the probability that a student is more than 79.96 inches tall?
Approximate the probability that \(X \geq 84\), using the empirical rule.
Approximate the probability that \(68 \leq X \leq 92\), using the empirical rule.

Question ID: 0255748862

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 4231 and a variance of 376996, and is denoted as \(X\).

What is the probability that an employee earns between 4088.28 and 4593.69 per month?
What is the probability that an employee earns less than 4548.47 per month?
What is the probability that an employee earns more than 3510.77 per month?
Approximate the probability that \(X \geq 4845\), using the empirical rule.
Approximate the probability that \(3003 \leq X \leq 4231\), using the empirical rule.

Question ID: 0260738443

Suppose that lifespans of tortoises is normally distributed with a mean of 96 and a variance of 144, and is denoted as \(X\).

What is the probability that a tortoise lives between 66.91 and 123.95 years?
What is the probability that a tortoise lives less than 127.44 years?
What is the probability that a tortoise lives more than 77.22 years?
Approximate the probability that \(X \leq 120\), using the empirical rule.
Approximate the probability that \(96 \leq X \leq 120\), using the empirical rule.

Question ID: 0468785218

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 930 and a variance of 2916, and is denoted as \(X\).

What is the probability that the bulb lasts between 817.67 and 952.68 hours?
What is the probability that the bulb lasts less than 920.7 hours?
What is the probability that the bulb lasts more than 857.12 hours?
Approximate the probability that \(X \geq 768\), using the empirical rule.
Approximate the probability that \(876 \leq X \leq 1038\), using the empirical rule.

Question ID: 0623688333

Suppose that lifespans of tortoises is normally distributed with a mean of 119 and a variance of 100, and is denoted as \(X\).

What is the probability that a tortoise lives between 116.97 and 120.88 years?
What is the probability that a tortoise lives less than 146.13 years?
What is the probability that a tortoise lives more than 117.84 years?
Approximate the probability that \(X \leq 129\), using the empirical rule.
Approximate the probability that \(89 \leq X \leq 129\), using the empirical rule.

Question ID: 0395978203

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1047 and a variance of 1849, and is denoted as \(X\).

What is the probability that the bulb lasts between 1006.86 and 1148.65 hours?
What is the probability that the bulb lasts less than 1160.84 hours?
What is the probability that the bulb lasts more than 967.89 hours?
Approximate the probability that \(X \leq 1047\), using the empirical rule.
Approximate the probability that \(1047 \leq X \leq 1133\), using the empirical rule.

Question ID: 0047376734

Suppose that heights of students in a class is normally distributed with a mean of 63 and a variance of 36, and is denoted as \(X\).

What is the probability that a student is between 59.15 and 72.71 inches tall?
What is the probability that a student is less than 73.13 inches tall?
What is the probability that a student is more than 56.91 inches tall?
Approximate the probability that \(X \geq 57\), using the empirical rule.
Approximate the probability that \(69 \leq X \leq 81\), using the empirical rule.

Question ID: 0092448222

Suppose that heights of students in a class is normally distributed with a mean of 82 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 74.05 and 87.89 inches tall?
What is the probability that a student is less than 88.21 inches tall?
What is the probability that a student is more than 76.81 inches tall?
Approximate the probability that \(X \geq 90\), using the empirical rule.
Approximate the probability that \(74 \leq X \leq 86\), using the empirical rule.

Question ID: 0713805422

Suppose that heights of students in a class is normally distributed with a mean of 69 and a variance of 49, and is denoted as \(X\).

What is the probability that a student is between 65.68 and 73.86 inches tall?
What is the probability that a student is less than 81.15 inches tall?
What is the probability that a student is more than 56.02 inches tall?
Approximate the probability that \(X \leq 69\), using the empirical rule.
Approximate the probability that \(48 \leq X \leq 69\), using the empirical rule.

Question ID: 0145659093

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 173 and a variance of 625, and is denoted as \(X\).

What is the probability that the apple weighs between 170.89 and 188.14 grams?
What is the probability that the apple weighs less than 238.09 grams?
What is the probability that the apple weighs more than 165.58 grams?
Approximate the probability that \(X \leq 98\), using the empirical rule.
Approximate the probability that \(198 \leq X \leq 223\), using the empirical rule.

Question ID: 0291843947

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 185 and a variance of 400, and is denoted as \(X\).

What is the probability that the apple weighs between 170.48 and 231.94 grams?
What is the probability that the apple weighs less than 233.62 grams?
What is the probability that the apple weighs more than 135.06 grams?
Approximate the probability that \(X \leq 185\), using the empirical rule.
Approximate the probability that \(125 \leq X \leq 145\), using the empirical rule.

Question ID: 0127234045

Suppose that heights of students in a class is normally distributed with a mean of 89 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 86.53 and 95.25 inches tall?
What is the probability that a student is less than 87.69 inches tall?
What is the probability that a student is more than 84.25 inches tall?
Approximate the probability that \(X \leq 101\), using the empirical rule.
Approximate the probability that \(77 \leq X \leq 81\), using the empirical rule.

Question ID: 0499250456

Suppose that heights of students in a class is normally distributed with a mean of 79 and a variance of 9, and is denoted as \(X\).

What is the probability that a student is between 78.02 and 84.19 inches tall?
What is the probability that a student is less than 83.17 inches tall?
What is the probability that a student is more than 71.57 inches tall?
Approximate the probability that \(X \geq 82\), using the empirical rule.
Approximate the probability that \(70 \leq X \leq 82\), using the empirical rule.

Question ID: 0617731606

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 103 and a variance of 289, and is denoted as \(X\).

What is the probability that the apple weighs between 98.82 and 115.42 grams?
What is the probability that the apple weighs less than 141.46 grams?
What is the probability that the apple weighs more than 72.21 grams?
Approximate the probability that \(X \geq 137\), using the empirical rule.
Approximate the probability that \(103 \leq X \leq 120\), using the empirical rule.

Question ID: 0764666887

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 969 and a variance of 5184, and is denoted as \(X\).

What is the probability that the bulb lasts between 884.27 and 1023.33 hours?
What is the probability that the bulb lasts less than 1006.87 hours?
What is the probability that the bulb lasts more than 780.9 hours?
Approximate the probability that \(X \leq 969\), using the empirical rule.
Approximate the probability that \(753 \leq X \leq 1041\), using the empirical rule.

Question ID: 0030679819

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1071 and a variance of 1156, and is denoted as \(X\).

What is the probability that the bulb lasts between 1067.17 and 1140.55 hours?
What is the probability that the bulb lasts less than 1154.84 hours?
What is the probability that the bulb lasts more than 1052.22 hours?
Approximate the probability that \(X \geq 1105\), using the empirical rule.
Approximate the probability that \(969 \leq X \leq 1105\), using the empirical rule.

Question ID: 0731139046

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1079 and a variance of 5329, and is denoted as \(X\).

What is the probability that the bulb lasts between 924.38 and 1260.62 hours?
What is the probability that the bulb lasts less than 1091.91 hours?
What is the probability that the bulb lasts more than 887.96 hours?
Approximate the probability that \(X \geq 933\), using the empirical rule.
Approximate the probability that \(933 \leq X \leq 1152\), using the empirical rule.

Question ID: 0667157880

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 2976 and a variance of 407044, and is denoted as \(X\).

What is the probability that an employee earns between 2261.11 and 3111.97 per month?
What is the probability that an employee earns less than 3285.32 per month?
What is the probability that an employee earns more than 2877.06 per month?
Approximate the probability that \(X \leq 4890\), using the empirical rule.
Approximate the probability that \(1062 \leq X \leq 4890\), using the empirical rule.

Question ID: 0235779184

Suppose that heights of students in a class is normally distributed with a mean of 78 and a variance of 25, and is denoted as \(X\).

What is the probability that a student is between 68.96 and 86.82 inches tall?
What is the probability that a student is less than 83.77 inches tall?
What is the probability that a student is more than 80.17 inches tall?
Approximate the probability that \(X \geq 63\), using the empirical rule.
Approximate the probability that \(78 \leq X \leq 83\), using the empirical rule.

Question ID: 0487684825

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 180 and a variance of 576, and is denoted as \(X\).

What is the probability that the apple weighs between 123.42 and 195.82 grams?
What is the probability that the apple weighs less than 241.55 grams?
What is the probability that the apple weighs more than 111.08 grams?
Approximate the probability that \(X \leq 252\), using the empirical rule.
Approximate the probability that \(180 \leq X \leq 252\), using the empirical rule.

Question ID: 0650972269

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1032 and a variance of 2916, and is denoted as \(X\).

What is the probability that the bulb lasts between 1022.5 and 1039.71 hours?
What is the probability that the bulb lasts less than 1187.2 hours?
What is the probability that the bulb lasts more than 1035.26 hours?
Approximate the probability that \(X \geq 1140\), using the empirical rule.
Approximate the probability that \(924 \leq X \leq 1032\), using the empirical rule.

Question ID: 0890767113

Suppose that heights of students in a class is normally distributed with a mean of 71 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 70.15 and 75.11 inches tall?
What is the probability that a student is less than 77.6 inches tall?
What is the probability that a student is more than 72.81 inches tall?
Approximate the probability that \(X \geq 83\), using the empirical rule.
Approximate the probability that \(63 \leq X \leq 71\), using the empirical rule.

Question ID: 0554537473

Suppose that heights of students in a class is normally distributed with a mean of 69 and a variance of 16, and is denoted as \(X\).

What is the probability that a student is between 61.65 and 73.5 inches tall?
What is the probability that a student is less than 71.95 inches tall?
What is the probability that a student is more than 64.02 inches tall?
Approximate the probability that \(X \leq 81\), using the empirical rule.
Approximate the probability that \(57 \leq X \leq 77\), using the empirical rule.

Question ID: 0171044340

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 3038 and a variance of 241081, and is denoted as \(X\).

What is the probability that an employee earns between 2020.83 and 3649.18 per month?
What is the probability that an employee earns less than 4143.4 per month?
What is the probability that an employee earns more than 1903.76 per month?
Approximate the probability that \(X \geq 4020\), using the empirical rule.
Approximate the probability that \(3038 \leq X \leq 4020\), using the empirical rule.

Question ID: 0543748861

Suppose that the average monthly income for employees in a company is normally distributed with a mean of 3778 and a variance of 336400, and is denoted as \(X\).

What is the probability that an employee earns between 3560.65 and 3916.27 per month?
What is the probability that an employee earns less than 5310.64 per month?
What is the probability that an employee earns more than 2455.72 per month?
Approximate the probability that \(X \leq 5518\), using the empirical rule.
Approximate the probability that \(2618 \leq X \leq 3778\), using the empirical rule.

Question ID: 0673206981

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 170 and a variance of 324, and is denoted as \(X\).

What is the probability that the apple weighs between 132.47 and 208.13 grams?
What is the probability that the apple weighs less than 198.22 grams?
What is the probability that the apple weighs more than 161.59 grams?
Approximate the probability that \(X \geq 116\), using the empirical rule.
Approximate the probability that \(152 \leq X \leq 170\), using the empirical rule.

Question ID: 0212598401

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 131 and a variance of 484, and is denoted as \(X\).

What is the probability that the apple weighs between 85.55 and 174.28 grams?
What is the probability that the apple weighs less than 143.54 grams?
What is the probability that the apple weighs more than 136.54 grams?
Approximate the probability that \(X \leq 65\), using the empirical rule.
Approximate the probability that \(65 \leq X \leq 153\), using the empirical rule.

Question ID: 0225140596

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1047 and a variance of 5041, and is denoted as \(X\).

What is the probability that the bulb lasts between 979.61 and 1053.85 hours?
What is the probability that the bulb lasts less than 1187.03 hours?
What is the probability that the bulb lasts more than 1018.13 hours?
Approximate the probability that \(X \geq 834\), using the empirical rule.
Approximate the probability that \(834 \leq X \leq 1047\), using the empirical rule.

Question ID: 0374766005

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 925 and a variance of 6400, and is denoted as \(X\).

What is the probability that the bulb lasts between 871.95 and 987.32 hours?
What is the probability that the bulb lasts less than 927.23 hours?
What is the probability that the bulb lasts more than 739.89 hours?
Approximate the probability that \(X \leq 925\), using the empirical rule.
Approximate the probability that \(845 \leq X \leq 1005\), using the empirical rule.

Question ID: 0847337400

Suppose that the lifespan of a lightbulb produced by a certain factory is normally distributed with a mean of 1083 and a variance of 3481, and is denoted as \(X\).

What is the probability that the bulb lasts between 979.81 and 1096.61 hours?
What is the probability that the bulb lasts less than 1243.5 hours?
What is the probability that the bulb lasts more than 935.49 hours?
Approximate the probability that \(X \leq 965\), using the empirical rule.
Approximate the probability that \(906 \leq X \leq 1142\), using the empirical rule.

Question ID: 0820035456

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 156 and a variance of 289, and is denoted as \(X\).

What is the probability that the apple weighs between 120.32 and 157.61 grams?
What is the probability that the apple weighs less than 195.36 grams?
What is the probability that the apple weighs more than 154.61 grams?
Approximate the probability that \(X \leq 156\), using the empirical rule.
Approximate the probability that \(139 \leq X \leq 173\), using the empirical rule.

Question ID: 0513869759

Suppose that the weight of an apple harvested by a farmer is normally distributed with a mean of 100 and a variance of 256, and is denoted as \(X\).

What is the probability that the apple weighs between 85.27 and 122.19 grams?
What is the probability that the apple weighs less than 107.59 grams?
What is the probability that the apple weighs more than 103.6 grams?
Approximate the probability that \(X \geq 68\), using the empirical rule.
Approximate the probability that \(52 \leq X \leq 116\), using the empirical rule.

Question ID: 0184755441

Self Assessment 9.3

Suppose that \(X \sim \text{Bin}(446, 0.31)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 222) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 136) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 335) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 117) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(346 \leq X < 442\).

Question ID: 0368643491

Suppose that \(X \sim \text{Bin}(425, 0.68)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 262) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 338) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 298) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 315) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(181 \leq X < 292\).

Question ID: 0714426979

Suppose that \(X \sim \text{Bin}(328, 0.17)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 169) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 301) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 162) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 241) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(45 \leq X < 130\).

Question ID: 0809020544

Suppose that \(X \sim \text{Bin}(147, 0.69)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 32) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 145) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 98) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 59) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(10 \leq X < 33\).

Question ID: 0474267339

Suppose that \(X \sim \text{Bin}(442, 0.63)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 290) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 417) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 69) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 302) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(8 \leq X < 323\).

Question ID: 0497215903

Suppose that \(X \sim \text{Bin}(141, 0.85)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 22) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 123) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 93) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 71) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(54 \leq X < 125\).

Question ID: 0113449406

Suppose that \(X \sim \text{Bin}(236, 0.26)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 49) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 24) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 47) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 17) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(33 \leq X < 127\).

Question ID: 0333982032

Suppose that \(X \sim \text{Bin}(467, 0.3)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 392) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 315) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 22) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 193) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(18 \leq X < 270\).

Question ID: 0751221690

Suppose that \(X \sim \text{Bin}(371, 0.69)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 227) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 330) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 120) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 295) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(240 \leq X < 311\).

Question ID: 0861147874

Suppose that \(X \sim \text{Bin}(191, 0.82)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 130) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 6) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 126) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 137) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(45 \leq X < 109\).

Question ID: 0992906981

Suppose that \(X \sim \text{Bin}(228, 0.25)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 141) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 61) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 158) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 32) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(53 \leq X < 123\).

Question ID: 0481474213

Suppose that \(X \sim \text{Bin}(151, 0.55)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 30) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 86) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 16) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 83) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(91 \leq X < 116\).

Question ID: 0151611655

Suppose that \(X \sim \text{Bin}(176, 0.48)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 70) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 52) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 69) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 48) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(108 \leq X < 149\).

Question ID: 0726668499

Suppose that \(X \sim \text{Bin}(223, 0.33)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 106) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 223) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 102) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 195) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(10 \leq X < 192\).

Question ID: 0525621997

Suppose that \(X \sim \text{Bin}(436, 0.22)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 78) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 17) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 272) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 152) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(420 \leq X < 432\).

Question ID: 0506500222

Suppose that \(X \sim \text{Bin}(155, 0.17)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 128) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 55) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 50) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 85) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(34 \leq X < 52\).

Question ID: 0500542082

Suppose that \(X \sim \text{Bin}(185, 0.15)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 137) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 56) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 156) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 69) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(34 \leq X < 173\).

Question ID: 0337525035

Suppose that \(X \sim \text{Bin}(364, 0.84)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 305) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 142) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 170) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 268) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(81 \leq X < 139\).

Question ID: 0578748815

Suppose that \(X \sim \text{Bin}(380, 0.36)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 338) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 265) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 371) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 177) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(105 \leq X < 306\).

Question ID: 0404395216

Suppose that \(X \sim \text{Bin}(495, 0.18)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 200) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 160) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 44) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 431) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(163 \leq X < 341\).

Question ID: 0898618802

Suppose that \(X \sim \text{Bin}(141, 0.33)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 73) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 22) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 39) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 60) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(55 \leq X < 130\).

Question ID: 0949391481

Suppose that \(X \sim \text{Bin}(199, 0.7)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 110) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 191) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 106) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 131) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(60 \leq X < 143\).

Question ID: 0013594579

Suppose that \(X \sim \text{Bin}(137, 0.66)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 45) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 69) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 73) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 0) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(120 \leq X < 128\).

Question ID: 0170515600

Suppose that \(X \sim \text{Bin}(189, 0.13)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 131) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 78) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 51) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 108) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(5 \leq X < 99\).

Question ID: 0871821880

Suppose that \(X \sim \text{Bin}(172, 0.18)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 127) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 40) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 144) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 80) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(69 \leq X < 95\).

Question ID: 0928294421

Suppose that \(X \sim \text{Bin}(175, 0.4)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 124) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 128) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 103) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 61) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(22 \leq X < 94\).

Question ID: 0994570140

Suppose that \(X \sim \text{Bin}(133, 0.22)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 98) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 25) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 28) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 8) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(36 \leq X < 130\).

Question ID: 0845377987

Suppose that \(X \sim \text{Bin}(266, 0.89)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 113) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 12) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 176) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 243) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(72 \leq X < 182\).

Question ID: 0843698542

Suppose that \(X \sim \text{Bin}(279, 0.43)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 87) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 67) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 25) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 192) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(90 \leq X < 182\).

Question ID: 0677077761

Suppose that \(X \sim \text{Bin}(283, 0.21)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 90) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 211) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 182) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 8) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(218 \leq X < 276\).

Question ID: 0169918132

Suppose that \(X \sim \text{Bin}(285, 0.69)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 264) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 157) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 93) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 255) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(61 \leq X < 263\).

Question ID: 0245851640

Suppose that \(X \sim \text{Bin}(439, 0.49)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 330) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 59) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 407) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 104) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(310 \leq X < 431\).

Question ID: 0979331221

Suppose that \(X \sim \text{Bin}(206, 0.15)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 107) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 126) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 125) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 198) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(62 \leq X < 189\).

Question ID: 0241268597

Suppose that \(X \sim \text{Bin}(451, 0.8)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 18) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 440) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 160) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 370) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(102 \leq X < 443\).

Question ID: 0303887609

Suppose that \(X \sim \text{Bin}(107, 0.36)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 31) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 46) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 9) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 100) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(88 \leq X < 95\).

Question ID: 0785166220

Suppose that \(X \sim \text{Bin}(393, 0.16)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 258) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 305) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 200) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 147) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(156 \leq X < 353\).

Question ID: 0928553188

Suppose that \(X \sim \text{Bin}(371, 0.23)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 228) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 192) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 310) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 34) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(157 \leq X < 189\).

Question ID: 0144214513

Suppose that \(X \sim \text{Bin}(451, 0.67)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 15) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 48) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 390) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 179) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(88 \leq X < 250\).

Question ID: 0257742687

Suppose that \(X \sim \text{Bin}(330, 0.5)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 60) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 299) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 132) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 153) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(148 \leq X < 191\).

Question ID: 0455671389

Suppose that \(X \sim \text{Bin}(414, 0.78)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 176) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 147) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 382) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 284) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(103 \leq X < 213\).

Question ID: 0844340952

Suppose that \(X \sim \text{Bin}(471, 0.66)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 125) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 10) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 156) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 112) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(177 \leq X < 303\).

Question ID: 0725438363

Suppose that \(X \sim \text{Bin}(495, 0.65)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 326) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 213) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 396) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 332) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(165 \leq X < 368\).

Question ID: 0099874064

Suppose that \(X \sim \text{Bin}(464, 0.44)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 282) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 305) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 245) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 420) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(136 \leq X < 251\).

Question ID: 0520053210

Suppose that \(X \sim \text{Bin}(140, 0.43)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 51) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 106) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 129) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 41) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(42 \leq X < 114\).

Question ID: 0410913728

Suppose that \(X \sim \text{Bin}(189, 0.62)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 116) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 17) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 179) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 42) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(2 \leq X < 60\).

Question ID: 0468054494

Suppose that \(X \sim \text{Bin}(242, 0.24)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 82) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 186) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 200) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 32) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(100 \leq X < 231\).

Question ID: 0000282538

Suppose that \(X \sim \text{Bin}(338, 0.89)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 54) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 113) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 293) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 186) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(133 \leq X < 308\).

Question ID: 0257567961

Suppose that \(X \sim \text{Bin}(346, 0.51)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 22) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 273) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 256) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 175) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(77 \leq X < 189\).

Question ID: 0505959293

Suppose that \(X \sim \text{Bin}(244, 0.81)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 184) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 102) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 141) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 181) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(144 \leq X < 186\).

Question ID: 0895008157

Suppose that \(X \sim \text{Bin}(396, 0.83)\). Suppose that \(W\) is a normally distributed random variable chosen to approximate \(X\).

What is \(E[W]\)?
What is \(\text{var}(W)\)?
We can write that \(P(X \leq 223) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X \geq 157) \approx P(W \geq w)\) for what value of \(w\)?
We can write that \(P(X < 231) \approx P(W \leq w)\) for what value of \(w\)?
We can write that \(P(X > 83) \approx P(W \geq w)\) for what value of \(w\)?
Approximate the probability that \(65 \leq X < 246\).

Question ID: 0745974071

Recall Example 5.3 for practice in this.↩︎
If it summed to \(1\) then this would not be a continuous random variable, since there would only be a countable number of possible events.↩︎
Like, \(1\) in a million, or \(1\) in a billion, or \(1\) in the number of atoms in the universe.↩︎
These are called singletons. We addressed these in terms of probability assignment using the language of singletons above. As a general rule, when working with continuous quantities, we simply ignore all of the singletons.↩︎
If you have taken calculus, you may recognize this process as feeling related to the first principle definition of a derivative. While it is often described in a slightly different way, this feeling of connection is intentional.↩︎
This is not a rare occurrence either. For instance, if we consider a random variable that will take on values in the interval \([0,0.5]\) with equal likelihood, the probability density function in this case will be \(f(x) = 2\).↩︎
Think about the fact that, while we may think of human adult heights as a continuous quantity, it is far more likely to observe a height around \(5\) feet \(6\) inches than around \(9\) feet \(2\) inches.↩︎
In the continuous case we cannot sum over the sample space, and so we must use techniques from calculus to mirror this process, for instance.↩︎
As a note, the integrate to one and sum to one properties for density functions and mass functions, respectively, are an additional example of a situation wherein the sum and integral can be interchanged for one another.↩︎
When \(F\) is not strictly invertible, we can instead consider the generalized inverse based on the right-continuity of \(F\), giving \(F^{-1}(p) = \inf\{x\in\mathbb{R}\mid p \leq F(x)\}\).↩︎
Which we have actually already seen.↩︎
Which is far and away the most important distribution (discrete or continuous) in all of probability and statistics.↩︎
The exponential is actually a special case of the gamma distribution, as are several other important named distributions, which will be brought up as required.↩︎
Sometimes called the continuous uniform distribution to distinguish it from its discrete counterpart.↩︎
In Example 9.1 we implicitly used the cumulative distribution function of the uniform. It is worth revisiting these probabilities knowing that this is the case.↩︎
For instance, in Example 8.6, we implicitly used a continuous uniform distribution to give the probability that Charles hits the dartboard. This type of reasoning is very prevalent.↩︎
See Section 9.12 for more details on this.↩︎
Note that, for instance, \(\binom{200}{75} = 168849997346404286704489530268603459022868706883102845056\). This is \(168\) septendecillion. This is \(3.2\) million times more than the number of possible arrangements of a chess board. This is a silly large number.↩︎
Doing so results in 0.0141898. Note, if we had used a binomial probability calculator instead, we would have gotten 0.0140627.↩︎
In fact, the actual probability here is 0.7824647.↩︎
The actual binomial probabilities here are 0.9519985, while the normal approximation is 0.959695.↩︎
William Gosset, was a statistician, chemist, and brewer who worked as the head brewer at Guinness. During his work there he was concerned with statistical problems related to testing the quality of ingredients. In this work, he made a discovery relating to the \(t\) distribution which was published in a scientific article under the pseudonym Student (hence, Student’s \(t\) distribution). Guinness preferred that their employees used pseudonyms when publishing scientific articles, perhaps to ensure that trade secrets were kept secret, and hence Student’s \(t\) was born.↩︎
The density function, for instance, is given by \[\frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\pi\nu}\Gamma(\frac{\nu}{2})}\left(1+\frac{x^2}{\nu}\right)^{-(\nu+1)/2},\] where \(\Gamma(\cdot)\) is the Gamma function, a mathematical expression touched on later.↩︎
Note, some authors instead parameterize the exponential distribution with the mean, \(\mu\). In this case, \(E[X] = \mu\), \(\text{var}(X) = \mu^2\), but the density will have \(\dfrac{1}{\mu}\) in place of \(\lambda\).↩︎
The exponential distribution shares this property with the geometric distribution, and can as such be thought of as a continuous analog to the geometric distribution.↩︎
As is the case with many distributions, some authors will use a different parametrization of the Gamma distribution. In particular, they may use parameters that equal \(\alpha\) and then \(1/\beta\), making the necessary substitutions in the different quantities.↩︎
Recall, the standard deviation is the square root of the variance.↩︎