8 The Named Discrete Distributions

8.1 General Named Distributions and the Discrete Uniform

So far, our discussion of probability distributions and their summaries has centered on general results for arbitrary probability mass functions. The basic premise has been that, by knowing a probability mass function, you are able to understand the complete behaviour of a random quantity. Directly from this mass function we are able to derive summaries for the behaviour, for instance describing the location and variability of the random variable. In short by knowing the probability mass function¹ we immediately understand how the random variable behaves. We have not, however, spent much time discussing where the probability mass functions actually come from.

We have seen one fairly general probability mass function, the one deriving from the equally likely outcomes model. This probability mass function is completely defined by the set of possible values that the random variable can take on. Suppose that we restrict our attention to the sample space being a set of $k$ integers from $a$ through to $a+k$.² When setup in this way, this distribution is often referred to as the discrete uniform distribution. Typically, we will use the values for the lower bound ($a$) and the upper bound ($b=a+k$) to define which discrete uniform we are discussing. If we say that $X$ follows a discrete uniform distribution with parameters $a$ and $b$ we are saying that $X$ is a random variable which has an equal probability of taking any of the integers from $a$ to $b$. Put differently, we have that \[p_X(x) = \begin{cases} \frac{1}{b-a+1} & x \in\{a,a+1,\dots,b\}\\ 0 & \text{otherwise}.\end{cases}\]

Whenever we want to say that $X$ follows a particular distribution, we use a mathematical shorthand to do so. Specifically, we write $X \sim \text{Distribution}(\text{parameters})$ to mean “$X$ follows the $\text{Distribution}$ with $\text{parameters}$.” For instance, if $X$ represents the results of a fair six-sided die roll, we can write $X\sim\text{Discrete Uniform}(1,6)$. We will typically shorten this to something like $X\sim\text{D.Unif}(1,6)$. Knowing the probability mass function of $X$, we also immediately can work out the expectation and variance for the random variable. Doing this results in $E[X] = \frac{a+b}{2}$ and $\text{var}(X) = \frac{(b-a+1)^2-1}{12}$. This means that simply by knowing that a random variable follows a discrete uniform distribution we also immediately know³ any of the properties that we have discussed up until this point.

Mean and Variance of Discrete Uniform

Recall that $E[X]$ is given by \[E[X] = \sum_{x\in\mathcal{X}} xp_X(x).\] Thus, if we take $X$ to be from the discrete uniform then \[\begin{align*} E[X] &= \sum_{x=a}^b x\frac{1}{b-a+1} \\ &= \frac{1}{b-a+1}\sum_{x=a}^b x \\ &= \frac{1}{b-a+1}\times\frac{1}{2}(b-a+1)(a+b) \\ &= \frac{a+b}{2}. \end{align*}\] For the variance, we can take the same derivation as above, this time solving $E[X^2]$. For this we get \[\begin{align*} E[X^2] &= \sum_{x=a}^b x^2\frac{1}{b-a+1} \\ &= \frac{1}{b-a+1}\sum_{x=a}^b x^2 \\ &= \frac{1}{b-a+1}\times\frac{1}{6}(b-a+1)(2a^2 + 2ab - a + 2b^2 + b) \\ &= \frac{2a^2 + 2ab - a + 2b^2 + b}{6}. \end{align*}\] Then, \[\begin{align*} \text{var}(X) &= E[X^2] - E[X]^2 \\ &= \frac{2a^2 + 2ab - a + 2b^2 + b}{6} - \left(\frac{a+b}{2}\right)^2 \\ &= \frac{8a^2 + 8ab - 4a + 8b^2 + 4b - 6a^2 - 12ab - 6b^2}{24} \\ &= \frac{2a^2 - 4ab - 4a + 4b + 2b^2}{24} \\ &= \frac{a^2 - 2ab - 2a + 2b + b^2}{12} \\ &= \frac{a^2 - 2ab - 2a + 2b + b^2 + 1 - 1}{12} \\ &= \frac{(b-a+1)^2 - 1}{12}. \end{align*}\]

This realization is particularly powerful. There are many real-world quantities which, through inspection, must follow a discrete uniform distribution. For instance, consider rolling a die. In the case of a die roll we take $a=1$, $b=6$, and immediately understand that $E[X] = 3.5$, that $\text{var}(X) = \frac{17}{6}$, and that the probability of each value is $\frac{1}{6}$. We could do the same calculations for any die with any sides labeled in consecutive order.

Example 8.1 (Charles and Sadie find Discrete Uniform Quantities) As Charles and Sadie begin to learn about named distributions, they decide that it is worthwhile to try to find examples of the named distributions around them. To do so, they start discussing a number of possibilities, each of them trying to describe whether and how different quantities obey the distribution.

For each of the following, help Charles and Sadie provide a justification of why a discrete uniform would (or would not be) appropriate, including a description of the parameters.

At a recent hockey game, Charles and Sadie were spectators and the 50-50 raffle was selected by choosing the seat number between $1$ and $4000$.
Charles’ sibling is having a child, and Charles has been thinking about what day of the week the child is going to be born on.
Sadie enjoys playing the birthday-guessing-game when in public, wherein Sadie attempts to guess what day of the year random patrons of the coffee shop were born on.
In their free time, Charles and Sadie enjoy playing role-playing games. These games often necessitate the rolling of dice, from the standard six-sided ones, through to large twenty-sided dice, or smaller three-sided ones.
Charles’ struggles to wake up in the mornings and as a result uses an alarm that plays a random song on a streaming music service. The song is selected from Charles’ library at random, keeping each morning exciting!

Solution

The winning seat can be treated as a random variable, $X$, which is distributed according to $\text{D.Unif}(1, 4000)$. The mean and variance are not particularly meaningful in this setting, however, each individual will have a constant probability of winning.
If the days of the week are labelled $1$ through $7$ (say, Sunday through Saturday), then it is reasonable to suspect that $Y$ representing the numerically-encoded day of the week will follow approximately a $\text{D. Unif}(1,7)$. It may be arguable that some days are less likely than others to be born on (empirically, Sundays appear to have about $0.12$ which is less than $1$ in $7$), however, it is probably a reasonably close approximation.
Here we can either view Sadie’s guess or the true birthday as the random quantity. If Sadie truly guesses at random then it is likely this will follow a $\text{D. Unif}(1, 365)$, being well-represented by the discrete uniform. For one’s true birthdays, if we are willing to ignore seasonal birth effects and leap years, then it is reasonable to assume that it too will be $\text{D. Unif}(1,365)$, however, these are both effects that do truly exist and would slightly alter from the uniform probabilities.
Each roll of the die gives a discrete uniform based on the number of sides that it has. For any $d$ sided die, we can represent it via a $\text{D. Unif}(1,d)$. In these types of games, the mean and variance are more pertinent than in most of the other examples we have discussed. Importantly, if we roll multiple dice and take a sum (or a maximum, minimum, etc.) these no longer will be described by the uniform distribution.
If Charles were to enumerate the songs on the streaming service with $1$ to $n$, then the played song may follow a $\text{D. Unif}(1, n)$ distribution.⁴

While the discrete uniform can be useful for real-world applications, it is also a comparatively simple distribution. The main point of this discussion is not actually to introduce the discrete uniform, but rather to introduce the concept of a named distribution. There are processes in the world which occur frequently enough, in a wide array of settings, with the same underlying structure for their uncertainty. If we study one version of these general processes we can derive the mass function, expectation, and variance for them. Then, we are easily able to describe the probabilistic behaviour of other quantities following a similar process. At that point, understanding the uncertainty of random quantities becomes a matter of matching the processes to the correct distribution, and then applying what we know about that distribution directly. While not every process will directly correspond to a known, named distribution, we can often get very close using just a handful of these.⁵

For each named distribution there is an underlying structure describing the scenarios in which it arises. For instance, for the discrete uniform, this is when there is a set of equally likely outcomes which can be described using consecutive integers. Once matched, there will is a probability mass function, an expected value, and a variance associated with the distribution. Importantly, all of these quantities will depend on some parameters. In the discrete uniform we used the parameters $a$ and $b$. These parameters specify which version of the distribution is relevant for the underlying scenario.

It is best to think of the named distributions as families of distributions, with specific iterations being dictated by the parameter values. If two processes follow the same distribution with different parameters they will not be identically distributed, they are simply drawn from the same family. If two processes have the same parameter values and the same underlying distribution, they are identically distributed and their probabilistic behaviour will be exactly the same. For instance, there is no probabilistic difference between rolling a fair, six-sided die or drawing a card at random from a set of $6$ cards labelled $1$ through $6$. There may be real-world differences which matter, but from a probabilistic point of view, they are exactly the same. This is a useful realization as it allows the use of simple models to understand more complex phenomenon.

8.2 The Bernoulli Distribution

Perhaps the best way to demonstrate the effectiveness of these simple models is to introduce one of the most basic named probability distribution, the Bernoulli distribution.⁶ The Bernoulli distribution characterizes any statistical experiment with a binary outcome when these results are denoted $0$ and $1$. The parameter that indexes the distribution is $p$, which gives the probability of observing a $1$. The most straightforward application of a Bernoulli random variable is the flip of a coin. Take $X=1$ if a head is shown, and $X=0$ if a tails is shown. Then $X\sim\text{Bern}(p)$⁷, with $p=0.5$. If $X\sim\text{Bern}(p)$ then we know that \[p_X(x) = \begin{cases} p^x(1-p)^{1-x} & x\in\{0,1\}\\ 0 & \text{otherwise}.\end{cases}\] Further, we can show that that $E[X] = p$ and $\text{var}(X) = p(1-p)$. We typically call $X=1$ a “success” and $X=0$ a “failure” when discussing Bernoulli random variables.

A coin flip is, by itself, not particularly interesting. However any statistical experiment with binary outcomes coded this way can be seen as a Bernoulli random variable. Suppose, for instance, you are interested in whether you will pass a particular course or not. There are two options, a “success” (passing) and a “failure” (failing), and the chances of this are governed by some probability $p$. Alternatively, suppose you want to know whether the next flight you take will land safely, or whether a particular medical treatment will effectively treat an illness. These are the same situations. Each of these scenarios is analyzed in exactly the same way as a coin toss: the probabilities change, but the underlying functions and mathematical objects do not. There is no probabilistic difference between determining whether a coin will come up heads or whether a plane will safely land.

Example 8.2 (Charles and Sadie find Bernoulli Quantities) In their ongoing quest to best understand the named distributions, Charles and Sadie continue their discussions of various quantities, and how they may fit a Bernoulli distribution.

For each of the following, help Charles and Sadie provide a justification of why a Bernoulli distribution would (or would not be) appropriate, including a description of the parameter.

Charles and Sadie think about entering their favourite coffee shop, and seeing whether or not there is seating available for them.
Charles thinks about the games that they have played deciding on who would have to pay, based on the outcomes of a few coin tosses.
Sadie is going on a trip shortly, and wonders whether or not the plane will be running on schedule.
Charles and Sadie are big sports fans, and want to know whether the local team will win the upcoming match.
Sadie wants to take out a book from the library, but is not sure whether it is available.

Solution

In this case we can treat $X=1$ as there being seating available (“success”) and $X=0$ as there not being seating available. The parameter, $p$ would be given by the probability that there is seating available, which is likely not a known probability directly.
In this case we can treat $X=1$ as Sadie having to pay, with $X=0$ as Charles having to pay. The parameter $p$ corresponds to the probability that Sadie pays, which in most of the original examples would have $p=0.5$.
In this case we can treat $X=1$ as the plane being on time, and $X=0$ as it being late. The parameter $p$ would correspond to the probability that the plane is late.
In this case we can treat $X=1$ as the team winning the game, and $X=0$ as them losing. The parameter $p$ would correspond to the probability that they win.
In this case we can treat $X=1$ as the book being available, and $X=0$ as it being not available. The parameter $p$ would correspond to the probability that it is available.

8.3 The Binomial Distribution

A natural extension to tossing a coin once and seeing if it comes up heads or not is tossing a coin $n$ times and counting how many times it comes up heads. If we take $X$ to be the number of “successes” in $n$ independent and identically distributed Bernoulli trials, then we say that $X$ has a binomial distribution. The binomial distribution is characterized by two different parameters, the number of trials that are being performed, denoted $n$, and the probability of a success on each trial, $p$. We write $X\sim\text{Bin}(n,p)$.

Example 8.3 (Missing All the Good Games) Charles and Sadie often will attend hockey games together for their local team. In order to keep their costs down, they try not to go to every single game. Instead, each time a game comes around that they can both attend, they roll a die. If it is a $3$ or higher, they go, otherwise they stay home. One season they are looking back over the $30$ games, and seeing which they attended and which they did not. The team won $19$ of the games, and lost the other $11$. However, of the $18$ games that Charles and Sadie attended that season, they saw all $11$ losses and only $7$ of the wins! They cannot help but feel like they got very unlucky.

How many wins should Charles and Sadie have expected to see?
What is the variance in the number of wins that they could have expected?
What is the probability that, for a season record of $19$ wins and $11$ losses, they would have been present for $7$ or fewer wins?

Solution

Suppose that we take $X$ to represent the number of winning games that Sadie and Charles are present for. In this case, looking back on the season, we know that $X$ is going to be binomial with $n=19$ and $p = \dfrac{2}{3}$, since they go if a $3$ or greater is rolled on the die. Thus, we can take $X \sim \text{Bin}(19, \dfrac{2}{3})$.

$E[X] = np = \dfrac{2}{3}(19) = 12.666$. Thus they should have expected to see around $12$ or $13$ wins.
$\text{var}(X) = np(1-p) = 4.222$.
We want $P(X \leq 7)$. For this we get \[\begin{align*} P(X \leq 7) &= \sum_{x=0}^7 p_X(x) \\ &= \sum_{x=0}^7 \binom{19}{x}\left(\frac{2}{3}\right)^x\left(\frac{1}{3}\right)^{19-x} \\ &= \frac{2876233}{387420489} \\ &\approx 0.0074. \end{align*}\] This leaves them very unlucky.

If we know that $X\sim\text{Bin}(n,p)$ then we also know that \[p_X(x) = \begin{cases} \binom{n}{x}p^x(1-p)^{n-x} & x\in\{0,1,\dots,n\} \\ 0 &\text{otherwise}.\end{cases}\] This is the first distribution we have seen which knowing the underlying distribution would not have immediately translated into knowing the probability mass function, which begins to illustrate why this is a useful area of study. We can work out that $E[X] = np$ and $\text{var}(X) = np(1-p)$.

Example 8.4 (Charles and Sadie find Binomial Quantities) The adventures in understanding named distributions continue, this time Charles ans Sadie wonder where they may find Binomial distributions.

For each of the following, help Charles and Sadie provide a justification of why a Binomial distribution would (or would not be) appropriate, including a description of the parameters.

Charles rolls ten, six-sided dice, counting up the number of them which show a $1$.
Charles and Sadie reflect on the record of who has paid during their past $20$ visits to the coffee shop.
Sadie starts playing on a baseball league that uses a pitching machine, and wants to know, without practicing, how many hits occur in the first $20$ at bats.
Charles and Sadie distribute flyers for an upcoming concert that their folk-punk band is putting on. They hand out $50$ flyers and are wondering how many people will show.
Charles and Sadie form a pub trivia team with some friends. One day, their friend who specializes in history is gone one day, and $5$ multiple choice history questions come up. They want to know what their score will be randomly guessing on those questions.

Solution

The number of dice showing a $1$ is represented by a $\text{Bin}(10, \dfrac{1}{6})$ distribution. Each die has an equal chance of showing a $1$, independently from all other rolls, and each roll will definitely be either a $1$ or not a $1$.
We can take $X$ to represent the number of times that Charles has paid. This will be given by a $\text{Bin}(20, 0.5)$ distribution. Each time both are equally likely to pay, independent of all other times, and one of them will always pay.
We can take $X$ to be the number of hits, and then claim that this will follow a $\text{Bin}(20, p)$ distribution, where $p$ is the probability that Sadie makes a hit. The caveats that the pitching machine is used and that Sadie does not practice are important since if different pitches were used, or different skill levels emerged as time progresses, then it may not satisfy the conditions of a binomial distribution.
Here we can take $X$, the number who attend the show, as a $\text{Bin}(50,p)$, where $p$ is the probability that any individual who saw the flyer attends the show. In order for this to hold we need to assume that all individuals choose to attend or not individually, without influence from anyone else, and that the probability is constant across different people.
Suppose that there are $4$ multiple choice options, then the number they answer correctly will follow a $\text{Bin}(5,0.25)$ distribution. Assuming that their guesses are independent across the different questions, and that they do not have a better sense for some questions than others.

Note that the binomial distribution can be constructed by summing independent and identically distributed Bernoulli variables. Specifically, if $X_1,\dots,X_n\stackrel{iid}{\sim}\text{Bern}(p)$⁸ then taking \[Y = \sum_{i=1}^n X_i\] gives a binomial distribution, with $n$ and $p$. To understand this intuitively, note that if a Bernoulli comes up $1$ when we get a heads on a single flip of the coin, then if we flip the coin $n$ times and count the number of heads this is the same as counting the number of $1$s from each corresponding Bernoulli trial. Once we know this construction, we can use the properties we have previously seen about independent random variables to work out the mean and variance for the distribution.

Construction of Binomial Random Variables

Suppose that we take $X_1,\dots,X_n \stackrel{iid}{\sim} \text{Bern}(p)$. Then, if we define \[Y = \sum_{i=1}^n X_i\] we can work out $E[Y]$ and $\text{var}(Y)$ directly. First, \[E[Y] = E\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n E[X_i] = nE[X_i] = np.\] Moreover, owing to independence we get \[\text{var}(Y) = \text{var}(\sum_{i=1}^n X_i) = \sum_{i=1}^n \text{var}(X_i) = np(1-p).\] These are the same as what was listed for the binomial directly. We are also able to derive the probability mass function of the binomial using this construction.

If we note that $P(X_1 = x) = p^{x}(1-p)^{1-x}$, then be independence we cna write the joint probability mass function as the product of these, which gives: \[\begin{multline*}P(X_1=x_1, X_2 = x_2, \dots, X_k = x_k) = p^{x_1}(1-p)^{1-x_1}p^{x_2}(1-p)^{1-x_2}\cdots p^{x_n}(1-p)^{1-x_n} \\ = p^{\sum_{i=1}^n x_i}(1-p)^{n-\sum_{i=1}^n x_i} = p^{y}(1-p)^{n-y}.\end{multline*}\] Consider how we could have $Y = k$, for some $k\in\{0,\dots,n\}$. In order for this to be the case we would require exactly $k$ of the $n$ Bernoulli random variables to be $1$ and the other $n-k$ to be $0$. So, for instance, we may have $\{X_1 = 1, X_2 = 1, \dots, X_k = 1, X_{k+1} = 0, \dots, X_n = 0\}$. If we consider choosing which of the $n$ trials should be $1$, we know that there will be $\binom{n}{k}$ of these, and so that gives the number of disjoint combinations that satisfy $Y=k$. Combining this with the joint probability mass function we worked out gives \[P(Y=y) = \binom{n}{k}p^k(1-p)^{n-k},\] as required.

It is important to note that, to get the binomial distribution, we have made several key assumptions. First, we are counting the number of successes in a fixed number of trials. In order for something to be binomially distributed, we must know in advance how many trials there are under consideration. Second, each of these trials must be independent of one another. The outcome on one cannot impact any of the others. Third, there must be a constant probability of success across all trials. If the probabilities are shifting overtime, then a binomial is no longer appropriate.

Example 8.5 (Charles’ and Sadie’s Binomial Mistakes) In trying to learn about the binomial distribution, Charles and Sadie identified several candidates for quantities which did not satisfy a binomial distribution. For each of the following, help Charles and Sadie understand why a Binomial distribution would not be appropriate.

Charles rolls ten dice, of various different sizes, counting up the number of them which show a $1$.
Charles and Sadie are considering the weather for the next week, thinking about how many days there will be rain.
Charles and Sadie consider handing out flyers for their band’s concert, and give $10$ flyers to a group of $10$ friends walking by.
Sadie is considering a particular major league baseball player, considering the number of hits in a set number of at bats.
Charles and Sadie are playing a game where they roll a die, then flip a coin the number of times that is shown on the die, counting up the total number of heads.

Solution

The issue in this case is that, if the dice have different numbers of sides, the probability that they show a $1$ will not be constant. As a result, there is no value of $p$ that gives the probability of success on each trial.
The issue in this case is two-fold. First, it is unlikely that there is going to be a constant probability of rain. Even if there is, or we treat it as though it will be, it is unlikely that one day is independent of the next, all the time. That is to say, today’s weather likely impacts tomorrows, removing independence.
In this case, it is unlikely that the group of $10$ friends will independently decide to go or not. Likely if one goes, many will, and vice versa.
The issue here is that batters will bat against different pitches, which changes the probability of a hit. That is, some pitchers are less talented, and thus there is a higher probability of getting a hit against them.
The issue here is that there is not a set number of trials. Instead, the number of trials is random and dependent on the outcome of a previous statistical experiment.

8.4 The Geometric Distribution

The binomial counted the number of successes in a fixed number of trials. We may be interested in a related question, namely “how many trials would be needed to see a success?” Instead of “how many heads in $n$ flips of a coin?” we may ask “how many flips of a coin to get a head?” Much like the binomial, these quantities will be intimately tied to the Bernoulli distribution. Once more we are envisioning a sequence of independent and identically distributed trials being performed. However, instead of knowing that we will stop after $n$ trials have been conducted, here we will only stop once we see a particular result. Any random quantities following this process are said to follow a geometric distribution. The geometric distribution is parameterized with a single parameter, $p$, the probability of success. We write $X\sim\text{Geo}(p)$, and have that \[p_X(x) = \begin{cases}(1-p)^{x-1}p & x \geq 1 \\ 0 & \text{otherwise}.\end{cases}\] If $X\sim\text{Geo}(p)$, then $E[X] = \frac{1}{p}$ and $\text{var}(X) = \frac{1-p}{p^2}$.

Example 8.6 (Charles Plays Darts) Sadie is a very accomplished darts player. Charles is not. Despite Sadie’s best efforts, when Charles plays darts it is essentially randomly choosing an area on the dartboard. In one friendly game, Charles decides to only aim at the highest scoring region of the board - the triple twenty. This region occupies about $0.9\%$ of the total area, and the two friends play with a rule where if Charles misses entirely, another dart is thrown. Charles is curious as to how many darts are going to be needed to be thrown until a triple twenty is hit.

Find the expected number of darts required.
Find the variance in the total number of darts required.
What is the probability that it takes more than $5$ total throws to get a triple twenty?

Solution

This is a geometric distribution with $p=0.009$. Let $X \sim \text{Geo}(p)$ represent the number of darts that Charles sees.

The expected number of darts required, $E[X]$ is given by $1/p$, which is $\dfrac{1}{0.009} = 111.\dot1$.
The variance of the expected number of darts, $\text{var}(X)$ is given by $\frac{1-p}{p^2} = 12234.5679$.
To find $P(X \geq 5)$ it is simpler to work with $P(X < 5) = P(X=1) + P(X=2) + P(X = 3) + P(X=4)$. Then we take \[\begin{align*} P(X \geq 5) &= 1 - P(X < 5) \\ &= 1 - (P(X=1) + P(X=2) + P(X = 3) + P(X=4))\\ &= 1 - (0.009)(1-0.009)^{1-1} - (0.009)(1-0.009)^{2-1} \\ &\quad - (0.009)(1-0.009)^{3-1} - (0.009)(1-0.009)^{4-1} \\ &= 1 - (0.009)[1 + 0.991 + 0.991^2 + 0.991^3] \\ &= 0.964483... \end{align*}\] Thus, with more than $96\%$ probability, Charles will take $X$ or more dart throws to hit the triple twenty.

The geometric distribution differs from other named distributions that we have considered in that the random variable can take on an infinite number of possible values. The probability that $X$ exceeds a very large threshold shrinks to $0$, however, there is no maximum value that can be observed. To form the geometric random variable we assume that we are performing independent and identically distributed Bernoulli trials, and that we stop only after the first observed success.⁹

Example 8.7 (Charles and Sadie find Geometric Quantities) Still working through their distributional knowledge, Charles and Sadie are now hoping to identify geometric quantities.

For each of the following, help Charles and Sadie provide a justification of why a Geometric distribution would (or would not be) appropriate, including a description of the parameter.

Charles continues to roll a six-sided die until a $6$ is gotten.
Sadie has paid for coffee for the last several times, they are both wondering how many more times until Charles will have to pay.
Charles is considering a new job which would require a whole lot of plane travel, and so Charles begins to wonder how many flights will run on time before the first delay.
Sadie, in a round of guess-their-birthday, starts to count the number of people it takes (guessing one birthday for each person) until a birthday is guessed correctly.
Charles and Sadie very much enjoy a particular brand of vegan peach yogurt, but it is hard to find. They want to consider how many stores they need to visit before they find it in stock.

Solution

This will be $\text{Geo}(\dfrac{1}{6})$, as the trials are all independent and identically distributed, and the rolling stops at the first success.
If we define “Charles has to pay” as a success, then the number of visits to the coffee shop, starting today, until Charles pays will be $\text{Geo}(\dfrac{1}{2})$. Each trial is independent and identically distributed, and we stop counting when Charles pays.
In order for this to follow a geometric distribution we would require that each plane is equally likely to be delayed, and that there is no influence from one plane to another. If so, we take $p$ to be the probability that a plane is delayed, and then $X$ is the number of flights up-to and including the first delayed flight, and $X\sim\text{Geo}(p)$.
Assuming that Sadie makes guesses independently of one another, each with a probability of $\dfrac{1}{365}$ of being correct, then this will be $X\sim\text{Geo}(\dfrac{1}{365})$.
If each store stocks with probability, $p$, then the total number of stores until they purchase will be $\text{Geo}(p)$. However, this will assume that each store is out-of-stock independently of each other store, and this seems unlikely to be the case supposing (for instance) a common supplier.

8.5 The Negative Binomial Distribution

A natural way to make the geometric distribution more flexible is to not stop after the first success, but rather after a set number of successes. That is, instead of flipping a coin until we see a head, we flip a coin until we see $r$ heads. Any random quantity which follows this general pattern is said to follow a negative binomial distribution. We use two parameters to describe the negative binomial distribution, $r$ the number of successes we are looking to achieve, and $p$ the probability of a success on any given trial. We write $X\sim\text{NB}(r,p)$. If we know that $X\sim\text{NB}(r,p)$, then we immediately get \[p_X(x) = \begin{cases}\binom{x-1}{r-1}p^r(1-p)^{x-r} & x\geq r \\ 0 &\text{otherwise}.\end{cases}\] Moreover, we have $E[X] = \frac{r}{p}$ and $\text{var}(X) = \frac{r(1-p)}{p^2}$. Setting $r=1$, we get the same quantities explored in the case of the geometric distribution. That is, if $X \sim \text{NB}(1,p)$ then we can also say that $X \sim \text{Geo}(p)$.¹⁰

Example 8.8 (Charles and Sadie Try to Balance the Dart Game) Charles and Sadie have been continuing to play darts quite often together, and though Charles is improving, Sadie’s expertise still makes it an unfair game. As a result, they consider playing alternative versions of the game in which Sadie is at a disadvantage in order to make things more fair. Charles has improved so that $20\%$ of the time, the aimed for area of the dart board is hit. Sadie, on the other hand, hits with $60\%$ accuracy. Suppose that they are considering a game where Charles has to hit a spot $3$ times, and then Sadie has to hit the same spot $r$ times. They are trying to figure out $r$ to make the game fair.

How many tosses will it take, on average, for Charles to hit the area on the target $3$ times?
What should Charles and Sadie make $r$, if they want it to take Sadie the same number of tosses on average as Charles?
If they set $r$ as in (b), who has a higher variance in the number of tosses it takes?
What is the probability that Charles wins before Sadie has a chance to win?
What is the probability that Sadie wins on the first available turn?

Solution

Let $X$ be the number of tosses it takes for Charles and $Y$ to be the number of tosses it takes for Sadie. We have that $X \sim \text{NB}(3, 0.2)$, while $Y\sim\text{NB}(r, 0.6)$.

We know that $E[X] = \dfrac{3}{0.2} = 15$.
We have that $E[Y] = \dfrac{r}{0.6}$. Setting this equal to $15$ gives \[\frac{r}{0.6} = 15 \implies r = 15(0.6) = 9.\] Thus, they should set $r = 9$.
We have that $\text{var}(X) = \dfrac{3(0.8)}{0.2^2} = 60$ while $\text{var}(Y) = \dfrac{9(0.4)}{0.6^2} = 10$. Thus, Charles has a far greater variance in the total number of tosses than Sadie.
In order for Charles to win before Sadie has a chance, this would require $X < 9$. Thus, \[\begin{align*} P(X < 9) &= \sum_{x=3}^8 p_X(x) \\ &= \sum_{x=3}^8 \binom{x-1}{2}(0.2)^3(0.8)^{x-3} \\ &= \left(\frac{0.2}{0.8}\right)^3\left[\binom{2}{2} + \binom{3}{2}(0.8) + \binom{4}{2}(0.8)^2 + \binom{5}{2}(0.8)^3 \right.\\ &\quad\left.+ \binom{6}{2}(0.8)^4 + \binom{7}{2}(0.8)^5\right] \\ &= \frac{79329}{390625} \approx 0.203. \end{align*}\] Thus, approximately $20\%$ of the time Charles will win before Sadie even can.
The probability that Sadie wins on the first turn is $P(Y = 9)$. We get \[p_Y(9) = \binom{8}{8}(0.6)^9(0.4)^{9-9} = \frac{19683}{1953125} = 0.010078.\] Thus it is only around a $1\%$ chance that Sadie wins on turn $9$, the earliest possible turn for it.

Example 8.9 (Charles and Sadie find Negative Binomial Quantities) Having mastered many different distributions, Charles and Sadie fix their attention of finding the negative binomial quantities in the world around them.

For each of the following, help Charles and Sadie provide a justification of why a negative binomial distribution would (or would not be) appropriate, including a description of the parameters.

Charles continues to roll a six-sided die until there have been a total of six $6$s seen.
Charles sets aside $\$100$ for coffee purchases in a different account. If Charles and Sadie’s order comes to $\$6.25$ per trip, how many trips until the account needs to be restocked.
Sadie decided that poker is very fun to play after the first time getting a royal flush.¹¹ Sadie is very interested how many more hands of poker are likely to be needed until this feeling comes around a few more times.
Charles is continuing to crochet. Charles wants to know how many granny squares are needed to be made until there are enough squares without any errors to give as holiday gifts this year.
Sadie and Charles need to sell a total of ten chocolate bars for their fundraiser. They want to know how many houses they will need to visit in order to achieve this.

Solution

Each trial here is independent, identically distributed with a constant probability. Charles stops after $6$ successes, and as a result the negative binomial is satisfied. $X$ will follows a $\text{NB}(6, \dfrac{1}{6})$ distribution.
Note that at $\$6.25$ per order, $\$100$ buys $16$ orders. As a result, this process will end after $16$ “successes”, which is to say, times when Charles has to pay. We know from past examples that the probability Charles pays is $0.5$, independent of all other cases, and as a result this will follow a $\text{NB}(16, 0.5)$ distribution.
The probability of getting a royal flush is constant in poker hands¹² Moreover, Sadie is interested in a set number of royal flushes being achieved (a few more maybe means $3$ or so), and as a result, this falls into the category of negative binomial with $r$ set to the number Sadie wants to see, and $p$ being the probability of seeing a royal flush, which is approximately $\dfrac{4}{\binom{52}{5}}$, depending on the type of poker being played.
Assuming that there are a set number of holiday gifts that Charles wants to give, then we can take this to be $r$ from the negative binomial distribution. Assuming that Charles’ odds of making a mistake on any granny square are constant at $p$, then we can take the probability of success as $1-p$. Under these assumptions, and assuming the squares are all independent of one another, then this will be $\text{NB}(r, 1-p)$.
If we assume that each house, independently, buys chocolate bars with a constant probability, $p$, then this will follow a $\text{NB}(10, p)$ distribution.

8.6 The Hypergeometric Distribution

One of the use cases demonstrated for the binomial distribution is drawing with replacement. In order for the binomial distribution to be relevant it must be the case that the probability of a success is unchanging, and correspondingly, if the process under consideration is random draws from a population then these draws must be with replacement. Otherwise the probabilities would shift.¹³ Suppose that we are wish to draw the ace of spades from a standard, shuffled deck of $52$ cards. If we begin drawing cards without returning them to the deck after each draw, the probability that the next draw is the ace of spades is increasing over the draws. At first, the probability is $\dfrac{1}{52}$. If the first card is not the ace of spades, then the next draw it will be $\dfrac{1}{51}$. This continues until eventually the probability will grow to be $1$. As a result, this type of scenario does not fit into the independent and identically distributed Bernoulli trials that we have been exploring.

We require a different setup to model drawing without replacement from a finite population. Suppose that our population consists of two types of items, “successes” and “failures”. If we are interested in counting how many successes we see in a set number of draws, then this random quantity will follow a hypergeometric distribution. The hypergeometric distribution is parameterized using three different parameters: the number of items in the population, $N$, the number of these which are considered successes, $M$, and the total number of items that are to be drawn without replacement, $n$. We write $X\sim\text{HG}(N,M,n)$. If $X\sim\text{HG}(N,M,n)$ then \[p_X(x) = \begin{cases}\frac{\binom{N-M}{n-x}\binom{M}{x}}{\binom{N}{n}} & x\in\{\max\{0,M-N+n\},\dots,\min\{n,M\}\} \\ 0 &\text{otherwise}.\end{cases}\] Moreover, $E[X] = \frac{nM}{N}$ and the variance is given by \[\text{var}(X) = n\frac{M}{N}\frac{N-M}{N}\frac{N-n}{N-1}.\]

Example 8.10 (Charles Sock Drawer) Charles firmly believes that socks should not be sold in pairs.¹⁴ As a result, Charles has decided to keep socks unpaired, free floating in the drawers. In Charles’ sock drawer there are $13$ individual white socks, $8$ individual black socks, and $9$ individual red socks. One day, Charles is trying to wear matching socks because of a fancy dinner party, however, it is dark when the socks are being selected.

If Charles takes two socks from the drawer, what is the probability that there is a matching pair of white socks?
If Charles takes two socks from the drawer, what is the probability that there is a matching pair of any colour?
If Charles takes $5$ socks, how many of them are expected to be red? What is the variance of the number of red socks?
How many socks should Charles take out in order to expect to receive at least $2$ black socks?

Solution

We can view this as a hypergeometric distribution, where the specific parameters depend on what we are defining as a success. There will always be $N=30$, and $n$ will correspond to the number of socks that are drawn.

Here there are $M=13$ successes, $N=30$, and $n=2$. We wish to know $p_X(2)$, and so we find \[p_X(2) = \frac{\binom{N-M}{n-x}\binom{M}{x}}{\binom{N}{n}} = \frac{\binom{30-13}{0}\binom{13}{2}}{\binom{30}{2}} = \frac{26}{145} \approx 0.1793.\]
We can say that $P(\text{Pair}) = P(\text{Pair of White}) + P(\text{Pair of Red}) + P(\text{Pair of Black})$. We found $P(\text{Pair of White})$ in (a), and the remaining terms will be similar, changing $M=9$ for the red socks, and $M=8$ for the black socks. Thus, \[\begin{align*} P(\text{Pair of Red}) &= \frac{\binom{30-9}{0}\binom{9}{2}}{\binom{30}{2}} \\ &= \frac{12}{145} \\ P(\text{Pair of Black}) &= \frac{\binom{30-8}{0}\binom{8}{2}}{\binom{30}{2}} \\ &= \frac{28}{435} \\ P(\text{Pair}) &= \frac{26}{145} + \frac{12}{145} + \frac{28}{435} \\ &= \frac{142}{435} \\ &= 0.3264. \end{align*}\] Thus, there is approximately a $33\%$ chance that Charles draws a pair of socks.
Here we have $M=9$ and $n=5$. Thus, we find \[E[X] = \frac{(5)(9)}{30} = 1.5,\] and so $1.5$ red socks are to be expected.¹⁵ For the variance, we get \[\text{var}(X) = 5\cdot\frac{9}{30}\cdot\frac{30-9}{30}\cdot\frac{30-5}{30-1} = \frac{105}{116} \approx 0.905.\]
In this case we want $M=8$. In order to have $E[X] \geq 2$ we require \[\frac{n(8)}{30} \geq 2 \implies n \geq \frac{2(30)}{8} = 7.5,\] and so Charles should draw at least $8$ socks in order to expect to have at least $2$ black socks in the set of drawn ones.

The Hypergeometric Distribution, Binomial Distribution, and Survey Sampling

The hypergeometric is closely linked to the binomial distribution. If we consider the population described in the hypergeometric setup then the probability of a success on the first draw is $p=\frac{M}{N}$. Note that $E[X] = np$, exactly the same as in the binomial. However, plugging this in for the variance we get $\text{var}(X) = np(1-p)\frac{N-n}{N-1}$. Notice that if $n=1$, this extra term is simply $1$, and for $n > 1$ it will be less than $1$. As a result, the variance of the hypergeometric is smaller than the variance of the corresponding binomial. This makes intuitive sense. In the hypergeometric setup, the fact that draws are without replacement means that as more draws go on the probability of observing a success increases, reducing the likelihood of long runs of no observed successes. There is a cap on the behaviour of the random quantity thanks to the finiteness of the population. Correspondingly, the multiplicative term by which the variance shrinks, $\frac{N-n}{N-1}$ is referred to as the finite population correction. This factor differentiates the behaviour of the hypergeometric and the binomial.

Note that as $N$ becomes very, very large, as long as $n$ is small by comparison, the finite population correction will approach $1$. In other words, drawing without replacement in a large enough sample behaves almost exactly the same as drawing with replacement in the same sample. The binomial distribution can be used to approximate the hypergeometric distribution, so long as the population is very large. Again, this makes sense intuitively. If you have a deck with a million cards in it, and you are going to draw $2$, whether or not you return the first one to the deck has very little bearing on the probabilities associated with this scenario. Generally, the binomial distribution is easier to work with, so this approximation can be useful in some settings.

These types of considerations are deeply important in the field of survey sampling. In survey sampling, researchers select individuals from a population of interest, and have them respond to questions, or collect information on the respondents. You can think of, for instance, surveys that the university sends out or Canada-wide surveys trying to gauge sentiment on various policies. Generally in a survey you are going to be sampling without replacement: you will not include the same person in your sample more than once. However, it may also be the case that you are taking a fairly small sample (say $n=1000$) from a very large population (say $N=40000000$), at which point the finite population correction factor equals $0.999975$. This may as well be $1$ and you can simplify matters by using binomial probabilities.

Example 8.11 (Charles and Sadie find Hypergeometric Quantities) Charles and Sadie have almost made it through the set of distributions that they want to learn, now moving on to the hypergeometric.

For each of the following, help Charles and Sadie provide a justification of why a hypergeometric distribution would (or would not be) appropriate, including a description of the parameters.

When streaming music, Charles will often shuffle the entire library. While listening through, Charles keeps tracks of the number of songs that come on which are favourites.
Sadie is considering the number of spades that are likely to show up in different poker hands, from different versions of the game where hands may not be $5$ cards.
Charles and Sadie run a book club with some of their closest friends. Before each meeting, they take an anonymous vote as to whether the book was enjoyed or not, so that they know the total number of individuals who actually enjoyed the reading. If they know how many people will show up to a meeting, they are interested in how many of those people will have enjoyed the book.
Sadie learns of black swans, and wants to understand how many are likely to be seen if Sadie starts to view swans at a swan sanctuary.
Charles and Sadie are invited to partake in a survey. The survey is concerned with the number of people living in their town who support investments into transit infrastructure.

Solution

This will be hypergeometric assuming that the shuffle algorithm does not play the same songs multiple times in a session. Here $N$ is the total number of songs in the library, $M$ is the number of songs which Charles considers to be favourites, and $n$ is the number that Charles decides to listen to.
Assuming that the carts are dealt without replacement this will be hypergeometric. There are $N=52$ total cards, $M=13$ spades, and then $n$ will correspond to the size of the hand (such as $5$ or $3$ or $8$).
This will be hypergeometric, assuming that there is actually random attendance at the meetings. Here, $M$ will correspond to the number of individuals who enjoyed the book, $N$ is the total size of the book club, and $n$ is the number of people who can attend any given meeting.
In order for this to be hypergeometric, we would need to assume that Sadie is able to tell apart the different swans, so as to not count them more than once. In this case, $M$ is the total number of black swans at the sanctuary, $N$ is the total number of swans at the sanctuary, and $n$ is the number of swans that Sadie looks at.
This will typically be a hypergeometric, as most surveys are without replacement. Here, $N$ is the size of the possible population of individuals being surveyed, $n$ is the size of the survey, and $M$ is the number of people in the town who support investments into transit infrastructure.

8.7 The Poisson Distribution

The hypergeometric strayed from the pattern of the previously introduced distributions by not being represented as a sequence of Bernoulli trials. However, it was still characterized by a sequence of repeated trials. While many statistical experiments can be framed in this way, there are of course processes which are not described by repeated trials. Consider, for instance, any process where something is observed for a set period of times and events may or may not occur during this interval. Perhaps you sit on the side of the road and count the number of cars traveling by a particular intersection over the course of an hour. Each car going by is an event, but in this setting, the number of events is the random quantity itself. None of the distributions discussed until this point are suited to this type of process.

When we have events which occur at a constant rate, and our interest is in the number of events which occur, then we can make use of the Poisson distribution.¹⁶ The Poisson distribution takes a single parameter, $\lambda$, which is the average rate of occurrence of the events over the time period we are interested in. We write $X\sim\text{Poi}(\lambda)$. If $X\sim\text{Poi}(\lambda)$ then \[p_X(x) = \begin{cases} \frac{e^{-\lambda}\lambda^x}{x!} & x \geq 0 \\ 0 &\text{otherwise}.\end{cases}\] Moreover, $E[X]=\lambda$ and $\text{var}(X) = \lambda$.¹⁷

Example 8.12 (Charles’ Novella Mistakes) Charles has decided to write a short novella. Hard at work, the novella turns out to be $105$ pages, at the time of completion. Charles sends a copy off to the printer excited to share it with Sadie. After printing, Charles realizes that the spellcheck on the program indicates that there is a total of $215$ errors. Mortified that these were not corrected before handing it over to Sadie, Charles starts to work out just how bad the situation is likely to be.

What is the average number of mistakes per page of the novella?
What is the variance for the number of mistakes per page in the novella?
What is the probability that there were no mistakes on the first page?
What is the probability that there were five or more mistakes on the first page?

Solution

On average there will be $\dfrac{215}{105} = \dfrac{43}{21}$ errors per page. We can take the distribution to be $\text{Poi}(\dfrac{43}{21})$.
The variance for a Poisson distribution is given by $\lambda$. Thus, it will be $\dfrac{215}{105} = \dfrac{43}{21}$.
Here we want $p_X(0)$. This is given by \[p_X(0) = \frac{e^{-43/21}(43/21)^0}{0!} = e^{-43/21} \approx 0.129.\] Thus, there is about a $13\%$ chance that there are no errors on the first page.
Here we want $P(X \geq 5) = 1 - P(X < 5) = 1 - (p_X(0) + p_X(1) + p_X(2) + p_X(3) + p_X(4))$. Solving this directly gives \[\begin{align*} P(X \geq 5) = 1 - P(X < 5) &= 1 - \sum_{x=0}^4 p_X(x) \\ &= 1 - \sum_{x=0}^4 \frac{e^{-43/21}(43/21)^x}{x!} \\ &\approx 0.0571. \end{align*}\] Thus, there is just over a $5\%$ chance of there being $5$ or more errors on the first page.

While the most common applications for the Poisson distribution have to do with the occurrences of events throughout time, it is also possible to view this as the occurrences of events throughout space. For instance, if there is a manufacturer producing rope, then the number of defects in a set length of rope is likely to follow the Poisson distribution. Similarly, in a set geographic area, the number of birds of a particular species is likely to follow a Poisson distribution. For the Poisson distribution, we are typically thinking that there is a rate at which events of interest occur, and we can use the Poisson distribution to model the total number of occurrences over some specified interval.

Example 8.13 (Charles and Sadie find Poisson Quantities) As the last named discrete distribution, Charles and Sadie are excitedly exploring quantities around them which may be explained by the Poisson distribution.

For each of the following, help Charles and Sadie provide a justification of why a Poisson distribution would (or would not be) appropriate, including a description of the parameter.

Charles got a small injury which required a trip to the emergency room. While there, Charles begins to count the number of people that arrive over the course of the next hour.
Sadie, while out exploring birds, decides to count the number of cardinals in a particular good viewing spot which is about $100m^2$ in size.
Charles, while crocheting, realizes that sometimes the yarn in use has defects itself. Charles begins to think about the number of defects in $200$ yards of yarn.
Charles and Sadie are sitting at a public park overlooking the water. They start to count the number of boats that pass by over the course of the two hours they sit there.
Sadie starts a blog sharing recipes for baking vegan breads, and begins to consider the number of visitors that show up to the site each day.

Solution

Taking $X$ to represent the number of individuals arriving to the emergency room in the next hour, this will reasonably follow a Poisson distribution. The parameter $\lambda$ would represent the number of individuals who arrive per hour, on average. It is counting arrivals per hour.
If Sadie has a sense of the number of cardinals on average per $100m^2$ area, then a Poisson will be appropriate, supposing that the birds are fairly uniformly spread out. The parameter $\lambda$ would be the average number of birds in that size of region. It is counting occurrences per area.
If Charles knows the average number of defects per $200$ yards of yarn, then this value can be taken to be $\lambda$. Supposing that the defects occur uniformly, without dependence (e.g., one defect makes more likely around it) then a Poisson distribution is appropriate. It is counting defects per length of yarn.
We would take $\lambda$ to represent the average number of boats in a two hour period passing by the location that they are sitting. Supposing that these happen independently, at roughly uniform rates, then a Poisson is likely appropriate. This would be counting arrivals per (two) hour(s).
If Sadie gets a measure of the average number of visitors per day to the website, then setting this to be $\lambda$ gives a reasonable representation of traffic patterns. We would likely want to assume that the arrivals are not more on some days (for instance, the weekends) than others, but under these assumptions having $X \sim \text{Poi}(\lambda)$ is likely reasonable.

8.7.1 The Poisson Process

One particularly useful feature of the Poisson distribution stems from the fact that, when events of interest occur at a constant rate overtime, we can find a relevant Poisson distribution to describe these occurrences. When we model events in this manner, we refer to it as a Poisson process.

The Poisson Process

Suppose that $X$ counts the number events over a period of time of length $t$. Further suppose that:

Events at interest happen at a constant rate overtime. Denote the rate as $\alpha$ (per unit time).
Events occur independently of one another, so that the occurrence of one event does not influence any others.
No two events occur at precisely the same time.

Then, the number of events that occur during the time interval $t$, $X$, are said to follow a Poisson process. Specifically, $X$ will follow a $\text{Poi}(\alpha t)$ distribution.

The utility of the Poisson process is that, supposing we can determine the average rate of occurrence for any events, and supposing that we are willing to make the independence and non-simultaneous assumptions for the process, the distribution of events will always be Poisson. For instance, if we know how many events occur per hour and want to know how many events will occur per year, so long as the assumptions still hold, we can scale up the rate of occurrences and continue to use a Poisson distribution. For this reason, the Poisson distribution is frequently deployed for modelling real-world phenomenon.

Example 8.14 (Sadie’s Vegan Bakery Aspirations) With the success of Sadie’s vegan baking blog, there is some excited chatter about the prospects of opening up a real-world bakery! Before committing to this investment, Sadie wants to have an idea of whether the bakery would really be sustainable, and if so, what the staffing needs would be. Based on Sadie’s market research, it is expected that $168$ customers would arrive per week.

What assumptions would Sadie need to make in order to model this as a Poisson process? Is this likely to be accurate in actuality?
Sadie figures that it is important to bake everything fresh each day. If the bakery would be open 8 hours a day, 7 days a week, on average how many customers are expected to show up each day?
If each customer purchases 2 items on average, what is the probability that Sadie sells out on a day if each morning $50$ items are baked?
Sadie is very concerned about the impact of waste on a successful business. Write an expression for the probability that Sadie has a certain amount of waste ($w$) given the preparation of $n$ baked good at the start of each day. Assume that customers purchase 2 items on average.

Solution

Sadie would need to be willing to assume that customers arrive at a constant rate overtime (throughout all hours of the day, days of the week, weeks of the year), that customer arrivals are independent of each other (one customer arriving does not impact any other customer arriving), and that no two customers arrive at precisely the same time. These are not very reasonable assumptions in practice. It is very likely that certain times of the day or certain days of the week would be more (or less) popular than others. Moreover, it seems likely that people may arrive in groups, violating the independence assumption.
If we make the assumptions regarding the Poisson process, then we know that the arrival rate, $\alpha$, is $168$ per week. A day is $8$ hours, out of the full $56$ available, and so it corresponds to $t = \dfrac{1}{7}$. Thus, we know that the number of customers arriving per day will follow a \[\text{Poi}(\frac{1}{7}\times 168) = \text{Poi}(24),\] distribution, and as such the expected number of customers will be $24$.
The number of purchases made by a customer is $2$. As a result, the number of purchases per day will be $2\times 24 = 48$. As a result, we can model the number of daily purchases as a $\text{Poi}(48)$ distribution. If we want to know what the probability that Sadie sells out, we want to know \[P(X \geq 50) = 1 - P(X < 50) = 1 - \sum_{x = 0}^{49} \frac{(48)^xe^{-48}}{x!}.\] Using a computer to calculate this gives 0.4054.
If Sadie prepares $n$ items, and wants to know the probability of having a certain amount of waste $w$ ($w \in \{0,1,\dots,n\}$), this can be analyzed using the same $\text{Poi}(48)$ from the previous part. Specifically, taking $X$ to be the number of items sold in a day, then Sadie will be $w$ waste if $n - X = w$, or equivalently $X = n + w$. Thus, \[P(W = w) = P(X = n + w) = \frac{(48)^{n+w}e^{-48}}{(n+w)!},\] for $w = \{1, \dots, n\}$. The probability that there is no waste, is \[P(W = 0) = P(X \geq n) = 1 - \sum_{x = 0}^{n-1}\frac{(48)^{x}e^{-48}}{x!}.\]

It is important to note that a Poisson process can be defined over space as well, not just time. For instance, if we know that errors occur in the manufacturing of a particular chemical at a rate of $1$ per kiloliter, then the number of errors when producing any volume of the chemicals will also follow a Poisson process. It is most common to discuss the units as events per time, but every other unit will function in the exact same manner.

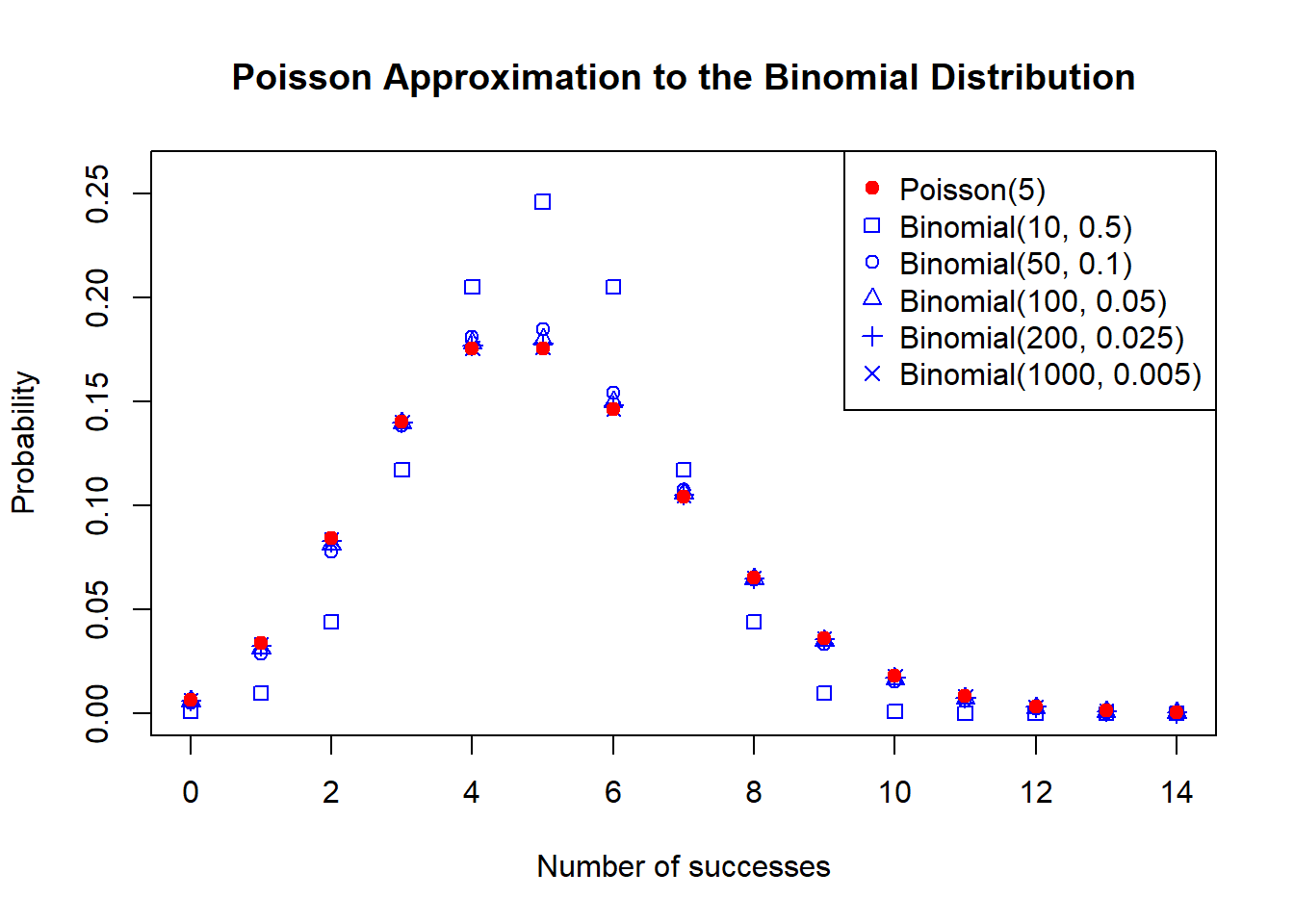
8.7.2 The Poisson Approximation to the Binomial

The Poisson distribution and binomial distribution may appear, on the surface, to be fairly disconnected from one another. The binomial distribution counts the number of successes in a discrete number of trials, where the number of trials is known in advance. The Poisson distribution, on the other hand, counts the number of events that occur not on repeated trials, but from a set window of observation. Both distributions are counting the number of occurrences of an event within a fixed observation window, but under very different circumstances.

Consider, however, what would happen if you began to perform more and more trials in a binomial experiment, with each of these trials getting closer and closer together. Intuitively, as this happens, the statistical experiment at hand begins to look more and more like the continual observation of a process. Consider, for instance, rolling a die every second and watching for when a certain outcome is observed. What if instead of once per second the die were rolled $100$ times per second? At some point, the individual experiments in the binomial experiment begin to blend together into a continuous process. At this point, the binomial and the Poisson distribution seemingly intersect: in each, you are observing a process in continuous time, counting the number of events that occur.

This intuition turns out to be correct. The Poisson distribution can be thought of as the limiting distribution to the binomial distribution. This can be formalized mathematically in the following manner.

Limiting Case of the Binomial

Suppose that $X \sim \text{Bin}(n, \dfrac{\lambda}{n})$, with $E[X] = \lambda$, and probability mass function \[p(x) = \binom{n}{x}\left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x}.\] Then, \[\lim_{n\to\infty} p(x) = \frac{\lambda^{x}e^{-\lambda}}{x!},\] which is the probability mass function for a $\text{Poi}(\lambda)$ random variable.

Note that in order for the limiting behaviour of this to hold the binomial requires both $n\to\infty$ as well as $p\to 0$ at such a rate so that $np = \lambda$ is constant. If this happens then in the limit the two distributions exactly coincide. While it is unlikely to perform a binomial experiment with infinite trials and a shrinking success probability, we may be faced with binomial distributions that have fairly high $n$ and fairly low $p$, and in these cases, we can use the Poisson to approximate binomial probabilities.¹⁸ In order to do so we say that if $X \sim \text{Binom}(n, p)$ then $X \dot\sim \text{Poi}(np)$, where $\dot\sim$ is read “is approximately distributed according to”.

The main utility of the approximation is that, especially for large $n$, binomial probabilities can be challenging to compute owing to the need to calculate $\dbinom{n}{x}$. Poisson probabilities are comparatively straightforward, and as such, when a rough calculation is all that is required, they can work fairly well.

Figure 8.1: This plot demonstrates the convergence of the Binomial to the Poisson (in terms of probability mass function) as $n$ increases and $p$ decreases, holding $np$ constant. The red circles show the Poisson probabilities, and the sequence of blue shapes show several binomial distributions, with increasing $n$, that are progressively better approximated by the Poisson.

Example 8.15 (Charles’ Viral Trick-Shot Attempt) Charles has been watching online videos of seemingly impossible “trick shots”, where individuals toss household objects to land in increasingly complex locations. Inspired by this trend, Charles decides to try a version of this at home, where the goal is to bounce a dime off of the table and have it land in an upright coke bottle. Suppose that the probability that Charles succeeds on any given attempt of this trick shot is $0.01$.

If Charles attempts the trick shot $100$ times, what is the probability that at least one of the attempts is successful?
How can the probability in part (a) be approximated using a Poisson? How close is the approximation.
Suppose that Charles instead attempts a new, more challenging the trick shot $1000$ times. This shot has a success probability of just $0.001$. What is the approximate probability that more than one of these attempts are successful?
Do you expect that the probability in (b) or (c) will be closer to the truth? Explain.

Solution

The number of successes will follow a $\text{Bin}(100, 0.01)$. We want to know $P(X \geq 1) = 1 - P(X = 0)$, and so we can compute this by calculating \[P(X = 0) = \binom{100}{0}(0.01)^{0}(0.99)^{100} = 0.99^{100}.\] As a result, the probability of at least one success is $1 - 0.99^{100}$ or approximately 0.634.
The binomial can be approximated using a $\text{Poi}(100(0.01)) = \text{Poi}(1)$ distribution. In this case, \[P(X \geq 1) = 1 - P(X = 0) \approx 1 - \frac{e^{-1}1^0}{0!} = 1 - e^{-1} \approx 0.632.\] This approximation differs from the truth by 0.0018471.
This binomial can be approximated using the same $\text{Poi}(1)$ distribution, since $1000(0.001) = 1$. As a result, the approximate probability will still be $1 - e^{-1} \approx 0.632$.
The probability in (c) should be closer to the truth since $n$ is larger and the approximation is based on the limit as $n\to\infty$. Thus, for larger $n$ with constant $np$, the approximation should improve. Indeed, if we check the actual binomial probability in the second case we get 0.6323046 which differs from the approximation by just 0.0001840164.

8.8 Using Named Distributions

While many other named, discrete distributions exist, these are the most common. When confronted with a problem in the real-world for which you wish to understand the uncertainty associated with it, a reasonable first step is to determine whether a named distribution is well-suited to representing the underlying phenomenon. Is it a situation with enumerated events which are equally likely? Use the discrete uniform. Is it a binary outcome? Use the Bernoulli. Are you counting the number of success in a fixed number of trials? Use the binomial. Are you running repeated trials until a (certain number of) success(es)? Use the geometric (or negative binomial). Are you sampling without replacement? Use the hypergeometric. Are you counting events over a fixed space? Use the Poisson.

Once identified, the distribution can be used in exactly the same way as any probability mass function. That is, we still require all the probability rules, event descriptions, and techniques from before. The difference in these cases is that we immediately have access to the correct form of the probability mass function, the expected value, and the variance.

An additional utility with this approach to solving probability questions is that, over time and repeated practice, you can build an intuition as to the behaviour of random variables following these various distributions. Probabilities in general can be deeply unintuitive. It can be hard to assess, without formally working it out, whether an event is likely or unlikely, let alone how likely an event is. However, the lack of intuition from our wider experience can be negated almost entirely by building of intuition through the repeated application of these distributions. You can start to gain a sense of how binomial random variables behave, being able to determine just from inspection whether events seem plausible or not. Much of the study of probability and statistics is about building a set of tools that can overcome the flaws in our intuitive reasoning regarding uncertainty. This comes only through practice, however, this framework of named distributions provides a very solid foundation to perform such practice.

8.8.1 Named Distributions in R

In R all of the named distributions that we have discussed, and in fact, many that we have not discussed, are implemented to make calculations easier. In particular, there are R functions which evaluate the probability mass function for the various distributions. Alongside these, there are also functions which calculate what we refer to as the cumulative probability¹⁹, which is to say the $P(X\leq k)$ for some value $k$. These functions generally are called d{distname}, where {distname} is the name of the relevant distribution. For instance, dbinom for the binomial, dpoi for the Poisson, and so forth. These will evaluate the probability mass function at the relevant values. In order to evaluate the cumulative probability at the specified values you would call p{distname}. These functions take in a parameter for the value to evaluate at, and then parameters that correspond to the various parameters from the distributions themselves.

Note that we have seen the sample function before, which is an implementation of the discrete uniform. To implement the Bernoulli, we can use the binomial distribution with $n=1$. It is a worthwhile exercise to see if you can use R to start answering the questions from this chapter, numerically. This is the first prominent use case for R programming which can save a tremendous amount of time, and is likely the first use case that becomes directly relevant to the course material.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 8.2

Suppose that $X$ follows a binomial distribution with $10$ trials, and a success probability of $0.63$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(8 \leq X < 9)$?

Question ID: 0577601380

Suppose that $X$ follows a binomial distribution with $14$ trials, and a success probability of $0.07$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(0 \leq X < 2)$?

Question ID: 0058224762

Suppose that $X$ follows a binomial distribution with $43$ trials, and a success probability of $0.49$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(18 \leq X < 22)$?

Question ID: 0221762135

Suppose that $X$ follows a binomial distribution with $74$ trials, and a success probability of $0.27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(22 \leq X < 26)$?

Question ID: 0240959638

Suppose that $X$ follows a binomial distribution with $77$ trials, and a success probability of $0.78$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 55)$?
What is $P(59 \leq X < 63)$?

Question ID: 0458230822

Suppose that $X$ follows a binomial distribution with $47$ trials, and a success probability of $0.87$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 21)$?
What is $P(42 \leq X < 43)$?

Question ID: 0807113275

Suppose that $X$ follows a binomial distribution with $99$ trials, and a success probability of $0.37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 55)$?
What is $P(37 \leq X < 40)$?

Question ID: 0568053499

Suppose that $X$ follows a binomial distribution with $93$ trials, and a success probability of $0.19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 63)$?
What is $P(18 \leq X < 21)$?

Question ID: 0337724052

Suppose that $X$ follows a binomial distribution with $81$ trials, and a success probability of $0.66$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 47)$?
What is $P(56 \leq X < 59)$?

Question ID: 0163732025

Suppose that $X$ follows a binomial distribution with $88$ trials, and a success probability of $0.09$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(8 \leq X < 9)$?

Question ID: 0319663412

Suppose that $X$ follows a binomial distribution with $81$ trials, and a success probability of $0.54$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(43 \leq X < 47)$?

Question ID: 0062680200

Suppose that $X$ follows a binomial distribution with $15$ trials, and a success probability of $0.6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(11 \leq X < 12)$?

Question ID: 0675832370

Suppose that $X$ follows a binomial distribution with $62$ trials, and a success probability of $0.7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(46 \leq X < 50)$?

Question ID: 0580146848

Suppose that $X$ follows a binomial distribution with $10$ trials, and a success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(3 \leq X < 6)$?

Question ID: 0192074064

Suppose that $X$ follows a binomial distribution with $57$ trials, and a success probability of $0.5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 52)$?
What is $P(28 \leq X < 30)$?

Question ID: 0916340638

Suppose that $X$ follows a binomial distribution with $33$ trials, and a success probability of $0.86$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(30 \leq X < 31)$?

Question ID: 0665226909

Suppose that $X$ follows a binomial distribution with $77$ trials, and a success probability of $0.09$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 50)$?
What is $P(5 \leq X < 7)$?

Question ID: 0999579375

Suppose that $X$ follows a binomial distribution with $87$ trials, and a success probability of $0.02$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(1 \leq X < 3)$?

Question ID: 0017773155

Suppose that $X$ follows a binomial distribution with $47$ trials, and a success probability of $0.71$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(33 \leq X < 34)$?

Question ID: 0049092148

Suppose that $X$ follows a binomial distribution with $37$ trials, and a success probability of $0.72$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(23 \leq X < 27)$?

Question ID: 0102400028

Suppose that $X$ follows a binomial distribution with $94$ trials, and a success probability of $0.39$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 43)$?
What is $P(38 \leq X < 39)$?

Question ID: 0334910130

Suppose that $X$ follows a binomial distribution with $25$ trials, and a success probability of $0.41$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(10 \leq X < 12)$?

Question ID: 0323321970

Suppose that $X$ follows a binomial distribution with $48$ trials, and a success probability of $0.07$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(4 \leq X < 8)$?

Question ID: 0921070512

Suppose that $X$ follows a binomial distribution with $19$ trials, and a success probability of $0.66$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(11 \leq X < 12)$?

Question ID: 0342591858

Suppose that $X$ follows a binomial distribution with $56$ trials, and a success probability of $0.43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 56)$?
What is $P(23 \leq X < 25)$?

Question ID: 0090420839

Suppose that $X$ follows a binomial distribution with $85$ trials, and a success probability of $0.79$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(65 \leq X < 69)$?

Question ID: 0416850773

Suppose that $X$ follows a binomial distribution with $47$ trials, and a success probability of $0.41$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(21 \leq X < 24)$?

Question ID: 0494418833

Suppose that $X$ follows a binomial distribution with $23$ trials, and a success probability of $0.14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(0 \leq X < 4)$?

Question ID: 0870140921

Suppose that $X$ follows a binomial distribution with $100$ trials, and a success probability of $0.18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 61)$?
What is $P(15 \leq X < 18)$?

Question ID: 0651015246

Suppose that $X$ follows a binomial distribution with $64$ trials, and a success probability of $0.9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 49)$?
What is $P(55 \leq X < 57)$?

Question ID: 0810956393

Suppose that $X$ follows a binomial distribution with $49$ trials, and a success probability of $0.44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(22 \leq X < 24)$?

Question ID: 0512220467

Suppose that $X$ follows a binomial distribution with $37$ trials, and a success probability of $0.89$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 18)$?
What is $P(29 \leq X < 31)$?

Question ID: 0541458088

Suppose that $X$ follows a binomial distribution with $81$ trials, and a success probability of $0.68$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(54 \leq X < 57)$?

Question ID: 0677241789

Suppose that $X$ follows a binomial distribution with $30$ trials, and a success probability of $0.78$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(25 \leq X < 29)$?

Question ID: 0574122083

Suppose that $X$ follows a binomial distribution with $10$ trials, and a success probability of $0.82$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(8 \leq X < 10)$?

Question ID: 0503486522

Suppose that $X$ follows a binomial distribution with $8$ trials, and a success probability of $0.33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(4 \leq X < 7)$?

Question ID: 0008967825

Suppose that $X$ follows a binomial distribution with $90$ trials, and a success probability of $0.59$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 54)$?
What is $P(53 \leq X < 57)$?

Question ID: 0022671826

Suppose that $X$ follows a binomial distribution with $62$ trials, and a success probability of $0.35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 54)$?
What is $P(21 \leq X < 25)$?

Question ID: 0876058761

Suppose that $X$ follows a binomial distribution with $23$ trials, and a success probability of $0.19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(3 \leq X < 4)$?

Question ID: 0738852166

Suppose that $X$ follows a binomial distribution with $69$ trials, and a success probability of $0.35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(23 \leq X < 25)$?

Question ID: 0045907888

Suppose that $X$ follows a binomial distribution with $61$ trials, and a success probability of $0.07$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 51)$?
What is $P(3 \leq X < 6)$?

Question ID: 0375970279

Suppose that $X$ follows a binomial distribution with $46$ trials, and a success probability of $0.85$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 30)$?
What is $P(38 \leq X < 40)$?

Question ID: 0713451911

Suppose that $X$ follows a binomial distribution with $61$ trials, and a success probability of $0.35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 56)$?
What is $P(23 \leq X < 25)$?

Question ID: 0617633396

Suppose that $X$ follows a binomial distribution with $63$ trials, and a success probability of $0.43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(25 \leq X < 28)$?

Question ID: 0781824572

Suppose that $X$ follows a binomial distribution with $57$ trials, and a success probability of $0.73$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(40 \leq X < 41)$?

Question ID: 0004983371

Suppose that $X$ follows a binomial distribution with $87$ trials, and a success probability of $0.13$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 20)$?
What is $P(9 \leq X < 11)$?

Question ID: 0037014528

Suppose that $X$ follows a binomial distribution with $95$ trials, and a success probability of $0.34$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 16)$?
What is $P(29 \leq X < 30)$?

Question ID: 0253407950

Suppose that $X$ follows a binomial distribution with $33$ trials, and a success probability of $0.85$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(25 \leq X < 29)$?

Question ID: 0465857544

Suppose that $X$ follows a binomial distribution with $13$ trials, and a success probability of $0.37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(2 \leq X < 6)$?

Question ID: 0092641454

Suppose that $X$ follows a binomial distribution with $70$ trials, and a success probability of $0.18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(13 \leq X < 16)$?

Question ID: 0742456507

Suppose that $X$ follows a binomial distribution with $12$ trials, and a success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(0 \leq X < 1)$?

Question ID: 0291294409

Suppose that $X$ follows a binomial distribution with $89$ trials, and a success probability of $0.88$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 71)$?
What is $P(80 \leq X < 82)$?

Question ID: 0521839552

Suppose that $X$ follows a binomial distribution with $57$ trials, and a success probability of $0.71$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(41 \leq X < 42)$?

Question ID: 0565821040

Suppose that $X$ follows a binomial distribution with $30$ trials, and a success probability of $0.2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(4 \leq X < 7)$?

Question ID: 0270367703

Suppose that $X$ follows a binomial distribution with $15$ trials, and a success probability of $0.7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(11 \leq X < 14)$?

Question ID: 0836586103

Suppose that $X$ follows a binomial distribution with $87$ trials, and a success probability of $0.31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 59)$?
What is $P(29 \leq X < 33)$?

Question ID: 0488896442

Suppose that $X$ follows a binomial distribution with $95$ trials, and a success probability of $0.44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(44 \leq X < 45)$?

Question ID: 0101718973

Suppose that $X$ follows a binomial distribution with $56$ trials, and a success probability of $0.75$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 55)$?
What is $P(45 \leq X < 48)$?

Question ID: 0628893088

Suppose that $X$ follows a binomial distribution with $86$ trials, and a success probability of $0.26$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(24 \leq X < 26)$?

Question ID: 0460254585

Suppose that $X$ follows a binomial distribution with $33$ trials, and a success probability of $0.35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(13 \leq X < 17)$?

Question ID: 0708222373

Suppose that $X$ follows a binomial distribution with $61$ trials, and a success probability of $0.37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(20 \leq X < 24)$?

Question ID: 0327931578

Suppose that $X$ follows a binomial distribution with $78$ trials, and a success probability of $0.61$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(50 \leq X < 52)$?

Question ID: 0044014920

Suppose that $X$ follows a binomial distribution with $90$ trials, and a success probability of $0.17$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 73)$?
What is $P(15 \leq X < 17)$?

Question ID: 0457841232

Suppose that $X$ follows a binomial distribution with $69$ trials, and a success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(2 \leq X < 3)$?

Question ID: 0677236475

Suppose that $X$ follows a binomial distribution with $9$ trials, and a success probability of $0.39$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(0 \leq X < 3)$?

Question ID: 0492034174

Suppose that $X$ follows a binomial distribution with $79$ trials, and a success probability of $0.32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 47)$?
What is $P(22 \leq X < 26)$?

Question ID: 0799383264

Suppose that $X$ follows a binomial distribution with $36$ trials, and a success probability of $0.94$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(34 \leq X < 36)$?

Question ID: 0456986275

Suppose that $X$ follows a binomial distribution with $89$ trials, and a success probability of $0.85$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(77 \leq X < 80)$?

Question ID: 0830189664

Suppose that $X$ follows a binomial distribution with $96$ trials, and a success probability of $0.45$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 57)$?
What is $P(46 \leq X < 48)$?

Question ID: 0950963342

Suppose that $X$ follows a binomial distribution with $47$ trials, and a success probability of $0.88$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(40 \leq X < 44)$?

Question ID: 0576529638

Suppose that $X$ follows a binomial distribution with $82$ trials, and a success probability of $0.88$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(70 \leq X < 72)$?

Question ID: 0988933489

Suppose that $X$ follows a binomial distribution with $23$ trials, and a success probability of $0.58$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(16 \leq X < 18)$?

Question ID: 0201995661

Suppose that $X$ follows a binomial distribution with $73$ trials, and a success probability of $0.05$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(5 \leq X < 7)$?

Question ID: 0872766351

Suppose that $X$ follows a binomial distribution with $27$ trials, and a success probability of $0.22$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(8 \leq X < 9)$?

Question ID: 0516083163

Suppose that $X$ follows a binomial distribution with $16$ trials, and a success probability of $0.03$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 \leq X < 2)$?

Question ID: 0868261120

Suppose that $X$ follows a binomial distribution with $55$ trials, and a success probability of $0.77$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(42 \leq X < 43)$?

Question ID: 0339883132

Suppose that $X$ follows a binomial distribution with $82$ trials, and a success probability of $0.54$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 38)$?
What is $P(43 \leq X < 47)$?

Question ID: 0774830937

Suppose that $X$ follows a binomial distribution with $67$ trials, and a success probability of $0.07$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 24)$?
What is $P(2 \leq X < 3)$?

Question ID: 0367462227

Suppose that $X$ follows a binomial distribution with $97$ trials, and a success probability of $0.1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 16)$?
What is $P(10 \leq X < 12)$?

Question ID: 0172944441

Suppose that $X$ follows a binomial distribution with $8$ trials, and a success probability of $0.2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(0 \leq X < 2)$?

Question ID: 0455337940

Suppose that $X$ follows a binomial distribution with $60$ trials, and a success probability of $0.79$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(49 \leq X < 50)$?

Question ID: 0990047363

Suppose that $X$ follows a binomial distribution with $18$ trials, and a success probability of $0.05$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(0 \leq X < 2)$?

Question ID: 0321305157

Suppose that $X$ follows a binomial distribution with $11$ trials, and a success probability of $0.31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(4 \leq X < 5)$?

Question ID: 0681489589

Suppose that $X$ follows a binomial distribution with $62$ trials, and a success probability of $0.43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(23 \leq X < 26)$?

Question ID: 0484511083

Suppose that $X$ follows a binomial distribution with $54$ trials, and a success probability of $0.78$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 24)$?
What is $P(43 \leq X < 47)$?

Question ID: 0969552051

Suppose that $X$ follows a binomial distribution with $10$ trials, and a success probability of $0.42$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(6 \leq X < 10)$?

Question ID: 0793848529

Suppose that $X$ follows a binomial distribution with $22$ trials, and a success probability of $0.69$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(16 \leq X < 17)$?

Question ID: 0714021505

Suppose that $X$ follows a binomial distribution with $77$ trials, and a success probability of $0.29$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 44)$?
What is $P(21 \leq X < 22)$?

Question ID: 0874556626

Suppose that $X$ follows a binomial distribution with $59$ trials, and a success probability of $0.16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 48)$?
What is $P(8 \leq X < 10)$?

Question ID: 0514951026

Suppose that $X$ follows a binomial distribution with $26$ trials, and a success probability of $0.56$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 24)$?
What is $P(16 \leq X < 20)$?

Question ID: 0943016909

Suppose that $X$ follows a binomial distribution with $100$ trials, and a success probability of $0.05$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 51)$?
What is $P(4 \leq X < 5)$?

Question ID: 0362185974

Suppose that $X$ follows a binomial distribution with $66$ trials, and a success probability of $0.57$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(37 \leq X < 40)$?

Question ID: 0486525502

Suppose that $X$ follows a binomial distribution with $72$ trials, and a success probability of $0.61$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 29)$?
What is $P(41 \leq X < 44)$?

Question ID: 0803671333

Suppose that $X$ follows a binomial distribution with $8$ trials, and a success probability of $0.85$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(6 \leq X < 8)$?

Question ID: 0098418025

Suppose that $X$ follows a binomial distribution with $44$ trials, and a success probability of $0.04$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(1 \leq X < 2)$?

Question ID: 0679287251

Suppose that $X$ follows a binomial distribution with $83$ trials, and a success probability of $0.71$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 50)$?
What is $P(59 \leq X < 62)$?

Question ID: 0032613507

Suppose that $X$ follows a binomial distribution with $19$ trials, and a success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 \leq X < 5)$?

Question ID: 0111557766

Suppose that $X$ follows a binomial distribution with $66$ trials, and a success probability of $0.88$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(59 \leq X < 63)$?

Question ID: 0255251272

Suppose that $X$ follows a binomial distribution with $46$ trials, and a success probability of $0.84$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 32)$?
What is $P(39 \leq X < 41)$?

Question ID: 0929869186

Suppose that $X$ follows a binomial distribution with $34$ trials, and a success probability of $0.75$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 30)$?
What is $P(22 \leq X < 24)$?

Question ID: 0592083896

Self Assessment 8.3

Suppose that $X$ follows a geometric distribution with success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(10 < X \leq 11)$?

Question ID: 0392324944

Suppose that $X$ follows a geometric distribution with success probability of $0.86$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0102347644

Suppose that $X$ follows a geometric distribution with success probability of $0.78$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0559920356

Suppose that $X$ follows a geometric distribution with success probability of $0.82$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0029478651

Suppose that $X$ follows a geometric distribution with success probability of $0.68$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 5)$?

Question ID: 0387686753

Suppose that $X$ follows a geometric distribution with success probability of $0.4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(3 < X \leq 5)$?

Question ID: 0166377439

Suppose that $X$ follows a geometric distribution with success probability of $0.19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(4 < X \leq 7)$?

Question ID: 0341099718

Suppose that $X$ follows a geometric distribution with success probability of $0.48$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(2 < X \leq 3)$?

Question ID: 0489312029

Suppose that $X$ follows a geometric distribution with success probability of $0.24$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(4 < X \leq 5)$?

Question ID: 0648694111

Suppose that $X$ follows a geometric distribution with success probability of $0.05$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 22)$?
What is $P(24 < X \leq 25)$?

Question ID: 0494465081

Suppose that $X$ follows a geometric distribution with success probability of $0.37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(3 < X \leq 5)$?

Question ID: 0946931649

Suppose that $X$ follows a geometric distribution with success probability of $0.59$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 6)$?

Question ID: 0925891111

Suppose that $X$ follows a geometric distribution with success probability of $0.66$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 2)$?

Question ID: 0145841055

Suppose that $X$ follows a geometric distribution with success probability of $0.22$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(5 < X \leq 9)$?

Question ID: 0084217360

Suppose that $X$ follows a geometric distribution with success probability of $0.93$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0657132962

Suppose that $X$ follows a geometric distribution with success probability of $0.46$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X \leq 4)$?

Question ID: 0330357664

Suppose that $X$ follows a geometric distribution with success probability of $0.19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(6 < X \leq 8)$?

Question ID: 0031979984

Suppose that $X$ follows a geometric distribution with success probability of $0.5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 4)$?

Question ID: 0955423517

Suppose that $X$ follows a geometric distribution with success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(5 < X \leq 6)$?

Question ID: 0399731618

Suppose that $X$ follows a geometric distribution with success probability of $0.09$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(10 < X \leq 13)$?

Question ID: 0937413403

Suppose that $X$ follows a geometric distribution with success probability of $0.12$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(7 < X \leq 9)$?

Question ID: 0749339353

Suppose that $X$ follows a geometric distribution with success probability of $0.75$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0668778208

Suppose that $X$ follows a geometric distribution with success probability of $0.66$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 4)$?

Question ID: 0077594624

Suppose that $X$ follows a geometric distribution with success probability of $0.52$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 3)$?

Question ID: 0349536513

Suppose that $X$ follows a geometric distribution with success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(6 < X \leq 9)$?

Question ID: 0133461597

Suppose that $X$ follows a geometric distribution with success probability of $0.35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X \leq 5)$?

Question ID: 0650646528

Suppose that $X$ follows a geometric distribution with success probability of $0.27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(4 < X \leq 7)$?

Question ID: 0676474633

Suppose that $X$ follows a geometric distribution with success probability of $0.24$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(4 < X \leq 6)$?

Question ID: 0810490700

Suppose that $X$ follows a geometric distribution with success probability of $0.16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(6 < X \leq 9)$?

Question ID: 0842385336

Suppose that $X$ follows a geometric distribution with success probability of $0.25$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(4 < X \leq 6)$?

Question ID: 0734277334

Suppose that $X$ follows a geometric distribution with success probability of $0.11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(6 < X \leq 9)$?

Question ID: 0022257570

Suppose that $X$ follows a geometric distribution with success probability of $0.92$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0142914810

Suppose that $X$ follows a geometric distribution with success probability of $0.74$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0069744382

Suppose that $X$ follows a geometric distribution with success probability of $0.58$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0361150155

Suppose that $X$ follows a geometric distribution with success probability of $0.18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(4 < X \leq 6)$?

Question ID: 0740283251

Suppose that $X$ follows a geometric distribution with success probability of $0.86$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0304148566

Suppose that $X$ follows a geometric distribution with success probability of $0.6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(2 < X \leq 5)$?

Question ID: 0901965444

Suppose that $X$ follows a geometric distribution with success probability of $0.26$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(3 < X \leq 7)$?

Question ID: 0948019096

Suppose that $X$ follows a geometric distribution with success probability of $0.62$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0619250571

Suppose that $X$ follows a geometric distribution with success probability of $0.9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0807695736

Suppose that $X$ follows a geometric distribution with success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(9 < X \leq 13)$?

Question ID: 0325112362

Suppose that $X$ follows a geometric distribution with success probability of $0.32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(3 < X \leq 4)$?

Question ID: 0499625166

Suppose that $X$ follows a geometric distribution with success probability of $0.49$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X \leq 5)$?

Question ID: 0907720813

Suppose that $X$ follows a geometric distribution with success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(9 < X \leq 12)$?

Question ID: 0535501705

Suppose that $X$ follows a geometric distribution with success probability of $0.7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 4)$?

Question ID: 0242170570

Suppose that $X$ follows a geometric distribution with success probability of $0.34$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(3 < X \leq 6)$?

Question ID: 0948100256

Suppose that $X$ follows a geometric distribution with success probability of $0.53$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 3)$?

Question ID: 0554493272

Suppose that $X$ follows a geometric distribution with success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(8 < X \leq 9)$?

Question ID: 0727876623

Suppose that $X$ follows a geometric distribution with success probability of $0.33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 6)$?

Question ID: 0989707255

Suppose that $X$ follows a geometric distribution with success probability of $0.65$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 4)$?

Question ID: 0992513267

Suppose that $X$ follows a geometric distribution with success probability of $0.38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 4)$?

Question ID: 0637716081

Suppose that $X$ follows a geometric distribution with success probability of $0.68$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 5)$?

Question ID: 0515368895

Suppose that $X$ follows a geometric distribution with success probability of $0.42$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 5)$?

Question ID: 0219370202

Suppose that $X$ follows a geometric distribution with success probability of $0.75$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 5)$?

Question ID: 0909638900

Suppose that $X$ follows a geometric distribution with success probability of $0.43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X \leq 3)$?

Question ID: 0004728038

Suppose that $X$ follows a geometric distribution with success probability of $0.1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(9 < X \leq 10)$?

Question ID: 0281782448

Suppose that $X$ follows a geometric distribution with success probability of $0.74$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0953558974

Suppose that $X$ follows a geometric distribution with success probability of $0.36$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 < X \leq 4)$?

Question ID: 0285637186

Suppose that $X$ follows a geometric distribution with success probability of $0.48$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X \leq 3)$?

Question ID: 0757087948

Suppose that $X$ follows a geometric distribution with success probability of $0.61$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 4)$?

Question ID: 0916648633

Suppose that $X$ follows a geometric distribution with success probability of $0.73$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0390615529

Suppose that $X$ follows a geometric distribution with success probability of $0.31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(4 < X \leq 5)$?

Question ID: 0888784942

Suppose that $X$ follows a geometric distribution with success probability of $0.73$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0411944571

Suppose that $X$ follows a geometric distribution with success probability of $0.63$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0000006972

Suppose that $X$ follows a geometric distribution with success probability of $0.01$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(93 < X \leq 97)$?

Question ID: 0400009183

Suppose that $X$ follows a geometric distribution with success probability of $0.44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X \leq 6)$?

Question ID: 0640636667

Suppose that $X$ follows a geometric distribution with success probability of $0.42$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 4)$?

Question ID: 0600786088

Suppose that $X$ follows a geometric distribution with success probability of $0.8$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0411974282

Suppose that $X$ follows a geometric distribution with success probability of $0.44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X \leq 3)$?

Question ID: 0694139641

Suppose that $X$ follows a geometric distribution with success probability of $0.77$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0142732120

Suppose that $X$ follows a geometric distribution with success probability of $0.02$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(38 < X \leq 40)$?

Question ID: 0048223060

Suppose that $X$ follows a geometric distribution with success probability of $0.1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(9 < X \leq 11)$?

Question ID: 0568339209

Suppose that $X$ follows a geometric distribution with success probability of $0.36$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 < X \leq 5)$?

Question ID: 0774471614

Suppose that $X$ follows a geometric distribution with success probability of $0.71$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 5)$?

Question ID: 0869465030

Suppose that $X$ follows a geometric distribution with success probability of $0.16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(6 < X \leq 8)$?

Question ID: 0626643572

Suppose that $X$ follows a geometric distribution with success probability of $0.1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(12 < X \leq 15)$?

Question ID: 0388385652

Suppose that $X$ follows a geometric distribution with success probability of $0.51$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 4)$?

Question ID: 0225457039

Suppose that $X$ follows a geometric distribution with success probability of $0.91$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 5)$?

Question ID: 0809571678

Suppose that $X$ follows a geometric distribution with success probability of $0.06$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(18 < X \leq 19)$?

Question ID: 0513651931

Suppose that $X$ follows a geometric distribution with success probability of $0.47$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X \leq 6)$?

Question ID: 0215452825

Suppose that $X$ follows a geometric distribution with success probability of $0.15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(8 < X \leq 11)$?

Question ID: 0668620555

Suppose that $X$ follows a geometric distribution with success probability of $0.14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(5 < X \leq 9)$?

Question ID: 0838611905

Suppose that $X$ follows a geometric distribution with success probability of $0.21$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(4 < X \leq 6)$?

Question ID: 0780609292

Suppose that $X$ follows a geometric distribution with success probability of $0.67$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 3)$?

Question ID: 0187105758

Suppose that $X$ follows a geometric distribution with success probability of $0.61$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 3)$?

Question ID: 0814715526

Suppose that $X$ follows a geometric distribution with success probability of $0.7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0329857039

Suppose that $X$ follows a geometric distribution with success probability of $0.38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X \leq 3)$?

Question ID: 0789705954

Suppose that $X$ follows a geometric distribution with success probability of $0.16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(5 < X \leq 7)$?

Question ID: 0498999664

Suppose that $X$ follows a geometric distribution with success probability of $0.71$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0739938990

Suppose that $X$ follows a geometric distribution with success probability of $0.44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X \leq 3)$?

Question ID: 0256136983

Suppose that $X$ follows a geometric distribution with success probability of $0.48$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 2)$?

Question ID: 0013721578

Suppose that $X$ follows a geometric distribution with success probability of $0.91$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0204861014

Suppose that $X$ follows a geometric distribution with success probability of $0.95$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 2)$?

Question ID: 0123250252

Suppose that $X$ follows a geometric distribution with success probability of $0.91$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 3)$?

Question ID: 0253673387

Suppose that $X$ follows a geometric distribution with success probability of $0.14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(7 < X \leq 11)$?

Question ID: 0855037065

Suppose that $X$ follows a geometric distribution with success probability of $0.55$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(2 < X \leq 3)$?

Question ID: 0099899388

Suppose that $X$ follows a geometric distribution with success probability of $0.08$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(9 < X \leq 11)$?

Question ID: 0177054595

Suppose that $X$ follows a geometric distribution with success probability of $0.82$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 5)$?

Question ID: 0638009318

Suppose that $X$ follows a geometric distribution with success probability of $0.83$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X \leq 4)$?

Question ID: 0031117501

Suppose that $X$ follows a geometric distribution with success probability of $0.51$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X \leq 4)$?

Question ID: 0569187685

Self Assessment 8.4

Suppose that $X$ follows a negative binomial distribution with success probability of $0.09$, requiring $3$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(21 \leq X \leq 22)$?

Question ID: 0881124894

Suppose that $X$ follows a negative binomial distribution with success probability of $0.51$, requiring $14$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 35)$?
What is $P(24 \leq X \leq 28)$?

Question ID: 0160803548

Suppose that $X$ follows a negative binomial distribution with success probability of $0.68$, requiring $18$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 45)$?
What is $P(35 \leq X \leq 36)$?

Question ID: 0701236102

Suppose that $X$ follows a negative binomial distribution with success probability of $0.87$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(9 \leq X \leq 13)$?

Question ID: 0907486291

Suppose that $X$ follows a negative binomial distribution with success probability of $0.35$, requiring $16$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 68)$?
What is $P(70 \leq X \leq 71)$?

Question ID: 0355635395

Suppose that $X$ follows a negative binomial distribution with success probability of $0.1$, requiring $14$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 67)$?
What is $P(180 \leq X \leq 183)$?

Question ID: 0202738286

Suppose that $X$ follows a negative binomial distribution with success probability of $0.73$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(15 \leq X \leq 19)$?

Question ID: 0488277231

Suppose that $X$ follows a negative binomial distribution with success probability of $0.69$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(9 \leq X \leq 11)$?

Question ID: 0595681709

Suppose that $X$ follows a negative binomial distribution with success probability of $0.34$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(50 \leq X \leq 51)$?

Question ID: 0073757587

Suppose that $X$ follows a negative binomial distribution with success probability of $0.21$, requiring $2$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 18)$?
What is $P(3 \leq X \leq 5)$?

Question ID: 0198369622

Suppose that $X$ follows a negative binomial distribution with success probability of $0.79$, requiring $7$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(14 \leq X \leq 16)$?

Question ID: 0197652174

Suppose that $X$ follows a negative binomial distribution with success probability of $0.09$, requiring $19$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 170)$?
What is $P(272 \leq X \leq 275)$?

Question ID: 0053610062

Suppose that $X$ follows a negative binomial distribution with success probability of $0.07$, requiring $3$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(78 \leq X \leq 79)$?

Question ID: 0596084847

Suppose that $X$ follows a negative binomial distribution with success probability of $0.35$, requiring $12$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(17 \leq X \leq 21)$?

Question ID: 0372228284

Suppose that $X$ follows a negative binomial distribution with success probability of $0.19$, requiring $15$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 121)$?
What is $P(128 \leq X \leq 129)$?

Question ID: 0740686557

Suppose that $X$ follows a negative binomial distribution with success probability of $0.12$, requiring $15$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 97)$?
What is $P(238 \leq X \leq 242)$?

Question ID: 0534085571

Suppose that $X$ follows a negative binomial distribution with success probability of $0.5$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(24 \leq X \leq 25)$?

Question ID: 0640843120

Suppose that $X$ follows a negative binomial distribution with success probability of $0.75$, requiring $14$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 31)$?
What is $P(31 \leq X \leq 33)$?

Question ID: 0693803336

Suppose that $X$ follows a negative binomial distribution with success probability of $0.36$, requiring $14$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 41)$?
What is $P(57 \leq X \leq 58)$?

Question ID: 0807581998

Suppose that $X$ follows a negative binomial distribution with success probability of $0.19$, requiring $11$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 92)$?
What is $P(98 \leq X \leq 102)$?

Question ID: 0988088402

Suppose that $X$ follows a negative binomial distribution with success probability of $0.2$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(50 \leq X \leq 51)$?

Question ID: 0900552758

Suppose that $X$ follows a negative binomial distribution with success probability of $0.36$, requiring $18$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 48)$?
What is $P(49 \leq X \leq 53)$?

Question ID: 0867623798

Suppose that $X$ follows a negative binomial distribution with success probability of $0.88$, requiring $18$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 40)$?
What is $P(31 \leq X \leq 33)$?

Question ID: 0927931379

Suppose that $X$ follows a negative binomial distribution with success probability of $0.06$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 137)$?
What is $P(283 \leq X \leq 284)$?

Question ID: 0555026235

Suppose that $X$ follows a negative binomial distribution with success probability of $0.29$, requiring $16$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 99)$?
What is $P(92 \leq X \leq 95)$?

Question ID: 0819421063

Suppose that $X$ follows a negative binomial distribution with success probability of $0.8$, requiring $19$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 22)$?
What is $P(25 \leq X \leq 29)$?

Question ID: 0070712360

Suppose that $X$ follows a negative binomial distribution with success probability of $0.15$, requiring $17$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 174)$?
What is $P(87 \leq X \leq 88)$?

Question ID: 0109198453

Suppose that $X$ follows a negative binomial distribution with success probability of $0.84$, requiring $17$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(18 \leq X \leq 22)$?

Question ID: 0601999566

Suppose that $X$ follows a negative binomial distribution with success probability of $0.32$, requiring $7$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(29 \leq X \leq 32)$?

Question ID: 0714768872

Suppose that $X$ follows a negative binomial distribution with success probability of $0.57$, requiring $11$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(15 \leq X \leq 17)$?

Question ID: 0985517238

Suppose that $X$ follows a negative binomial distribution with success probability of $0.2$, requiring $13$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 121)$?
What is $P(118 \leq X \leq 122)$?

Question ID: 0829464018

Suppose that $X$ follows a negative binomial distribution with success probability of $0.73$, requiring $3$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(4 \leq X \leq 6)$?

Question ID: 0572419011

Suppose that $X$ follows a negative binomial distribution with success probability of $0.7$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(8 \leq X \leq 9)$?

Question ID: 0775724595

Suppose that $X$ follows a negative binomial distribution with success probability of $0.87$, requiring $12$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(25 \leq X \leq 26)$?

Question ID: 0624817324

Suppose that $X$ follows a negative binomial distribution with success probability of $0.69$, requiring $14$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 38)$?
What is $P(22 \leq X \leq 26)$?

Question ID: 0025232094

Suppose that $X$ follows a negative binomial distribution with success probability of $0.31$, requiring $11$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(16 \leq X \leq 17)$?

Question ID: 0039647331

Suppose that $X$ follows a negative binomial distribution with success probability of $0.63$, requiring $8$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(15 \leq X \leq 19)$?

Question ID: 0739014248

Suppose that $X$ follows a negative binomial distribution with success probability of $0.67$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(28 \leq X \leq 30)$?

Question ID: 0029062111

Suppose that $X$ follows a negative binomial distribution with success probability of $0.27$, requiring $12$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(78 \leq X \leq 79)$?

Question ID: 0219628637

Suppose that $X$ follows a negative binomial distribution with success probability of $0.61$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 20)$?
What is $P(7 \leq X \leq 11)$?

Question ID: 0334046900

Suppose that $X$ follows a negative binomial distribution with success probability of $0.81$, requiring $17$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(36 \leq X \leq 38)$?

Question ID: 0572244361

Suppose that $X$ follows a negative binomial distribution with success probability of $0.91$, requiring $7$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(13 \leq X \leq 14)$?

Question ID: 0614282275

Suppose that $X$ follows a negative binomial distribution with success probability of $0.21$, requiring $2$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(8 \leq X \leq 9)$?

Question ID: 0571854032

Suppose that $X$ follows a negative binomial distribution with success probability of $0.79$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 16)$?
What is $P(12 \leq X \leq 13)$?

Question ID: 0974054119

Suppose that $X$ follows a negative binomial distribution with success probability of $0.23$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 22)$?
What is $P(32 \leq X \leq 34)$?

Question ID: 0341110239

Suppose that $X$ follows a negative binomial distribution with success probability of $0.85$, requiring $2$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(2 \leq X \leq 4)$?

Question ID: 0463987172

Suppose that $X$ follows a negative binomial distribution with success probability of $0.35$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 48)$?
What is $P(48 \leq X \leq 49)$?

Question ID: 0362916059

Suppose that $X$ follows a negative binomial distribution with success probability of $0.49$, requiring $8$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(30 \leq X \leq 33)$?

Question ID: 0625335146

Suppose that $X$ follows a negative binomial distribution with success probability of $0.7$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(5 \leq X \leq 9)$?

Question ID: 0483199994

Suppose that $X$ follows a negative binomial distribution with success probability of $0.28$, requiring $16$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 59)$?
What is $P(44 \leq X \leq 48)$?

Question ID: 0868620735

Suppose that $X$ follows a negative binomial distribution with success probability of $0.27$, requiring $13$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 32)$?
What is $P(56 \leq X \leq 58)$?

Question ID: 0932649592

Suppose that $X$ follows a negative binomial distribution with success probability of $0.82$, requiring $17$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(20 \leq X \leq 23)$?

Question ID: 0844828538

Suppose that $X$ follows a negative binomial distribution with success probability of $0.61$, requiring $19$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 20)$?
What is $P(58 \leq X \leq 62)$?

Question ID: 0024519831

Suppose that $X$ follows a negative binomial distribution with success probability of $0.02$, requiring $15$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 438)$?
What is $P(759 \leq X \leq 760)$?

Question ID: 0483513440

Suppose that $X$ follows a negative binomial distribution with success probability of $0.2$, requiring $18$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 149)$?
What is $P(168 \leq X \leq 172)$?

Question ID: 0548590195

Suppose that $X$ follows a negative binomial distribution with success probability of $0.04$, requiring $11$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 537)$?
What is $P(499 \leq X \leq 501)$?

Question ID: 0476961942

Suppose that $X$ follows a negative binomial distribution with success probability of $0.86$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(8 \leq X \leq 10)$?

Question ID: 0885514756

Suppose that $X$ follows a negative binomial distribution with success probability of $0.31$, requiring $8$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(29 \leq X \leq 32)$?

Question ID: 0477985072

Suppose that $X$ follows a negative binomial distribution with success probability of $0.51$, requiring $13$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 19)$?
What is $P(32 \leq X \leq 36)$?

Question ID: 0354307597

Suppose that $X$ follows a negative binomial distribution with success probability of $0.61$, requiring $6$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(14 \leq X \leq 17)$?

Question ID: 0136246571

Suppose that $X$ follows a negative binomial distribution with success probability of $0.79$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(15 \leq X \leq 19)$?

Question ID: 0455380749

Suppose that $X$ follows a negative binomial distribution with success probability of $0.03$, requiring $11$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 182)$?
What is $P(466 \leq X \leq 468)$?

Question ID: 0333753619

Suppose that $X$ follows a negative binomial distribution with success probability of $0.02$, requiring $18$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 165)$?
What is $P(1485 \leq X \leq 1486)$?

Question ID: 0572900091

Suppose that $X$ follows a negative binomial distribution with success probability of $0.04$, requiring $15$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 216)$?
What is $P(256 \leq X \leq 257)$?

Question ID: 0307690735

Suppose that $X$ follows a negative binomial distribution with success probability of $0.75$, requiring $10$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(13 \leq X \leq 14)$?

Question ID: 0087264257

Suppose that $X$ follows a negative binomial distribution with success probability of $0.33$, requiring $7$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(22 \leq X \leq 26)$?

Question ID: 0059596212

Suppose that $X$ follows a negative binomial distribution with success probability of $0.75$, requiring $19$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(26 \leq X \leq 27)$?

Question ID: 0023322200

Suppose that $X$ follows a negative binomial distribution with success probability of $0.3$, requiring $5$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(32 \leq X \leq 36)$?

Question ID: 0909998106

Suppose that $X$ follows a negative binomial distribution with success probability of $0.71$, requiring $15$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(19 \leq X \leq 21)$?

Question ID: 0695958189

Suppose that $X$ follows a negative binomial distribution with success probability of $0.84$, requiring $8$ successes.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(20 \leq X \leq 23)$?

Question ID: 0346330214

Self Assessment 8.5

Suppose that $X$ follows a hypergeometric distribution with $N = 27$, $M = 17$, and $n = 8$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(5 < X < 7)$?

Question ID: 0920303065

Suppose that $X$ follows a hypergeometric distribution with $N = 92$, $M = 38$, and $n = 26$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(12 < X < 14)$?

Question ID: 0488005392

Suppose that $X$ follows a hypergeometric distribution with $N = 84$, $M = 35$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(2 < X < 6)$?

Question ID: 0538944768

Suppose that $X$ follows a hypergeometric distribution with $N = 57$, $M = 28$, and $n = 9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 < X < 6)$?

Question ID: 0334383014

Suppose that $X$ follows a hypergeometric distribution with $N = 45$, $M = 32$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 5)$?

Question ID: 0352785795

Suppose that $X$ follows a hypergeometric distribution with $N = 53$, $M = 29$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(12 < X < 15)$?

Question ID: 0275021877

Suppose that $X$ follows a hypergeometric distribution with $N = 19$, $M = 7$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X < 4)$?

Question ID: 0617055454

Suppose that $X$ follows a hypergeometric distribution with $N = 94$, $M = 29$, and $n = 9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(4 < X < 7)$?

Question ID: 0861683655

Suppose that $X$ follows a hypergeometric distribution with $N = 43$, $M = 12$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 5)$?

Question ID: 0493354907

Suppose that $X$ follows a hypergeometric distribution with $N = 14$, $M = 9$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 4)$?

Question ID: 0272287339

Suppose that $X$ follows a hypergeometric distribution with $N = 41$, $M = 23$, and $n = 7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(4 < X < 8)$?

Question ID: 0127760360

Suppose that $X$ follows a hypergeometric distribution with $N = 52$, $M = 37$, and $n = 11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(7 < X < 10)$?

Question ID: 0746143315

Suppose that $X$ follows a hypergeometric distribution with $N = 78$, $M = 38$, and $n = 14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(3 < X < 6)$?

Question ID: 0471489798

Suppose that $X$ follows a hypergeometric distribution with $N = 20$, $M = 6$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(3 < X < 5)$?

Question ID: 0344395231

Suppose that $X$ follows a hypergeometric distribution with $N = 96$, $M = 39$, and $n = 23$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(13 < X < 17)$?

Question ID: 0594834110

Suppose that $X$ follows a hypergeometric distribution with $N = 18$, $M = 9$, and $n = 9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(5 < X < 8)$?

Question ID: 0802368639

Suppose that $X$ follows a hypergeometric distribution with $N = 68$, $M = 46$, and $n = 10$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(4 < X < 8)$?

Question ID: 0346355858

Suppose that $X$ follows a hypergeometric distribution with $N = 14$, $M = 10$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 6)$?

Question ID: 0990760336

Suppose that $X$ follows a hypergeometric distribution with $N = 17$, $M = 11$, and $n = 6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(5 < X < 7)$?

Question ID: 0727221610

Suppose that $X$ follows a hypergeometric distribution with $N = 26$, $M = 8$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 4)$?

Question ID: 0980248854

Suppose that $X$ follows a hypergeometric distribution with $N = 58$, $M = 34$, and $n = 14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(5 < X < 9)$?

Question ID: 0904266685

Suppose that $X$ follows a hypergeometric distribution with $N = 68$, $M = 43$, and $n = 18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(10 < X < 13)$?

Question ID: 0848803015

Suppose that $X$ follows a hypergeometric distribution with $N = 99$, $M = 43$, and $n = 35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(15 < X < 18)$?

Question ID: 0538825865

Suppose that $X$ follows a hypergeometric distribution with $N = 30$, $M = 22$, and $n = 7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(5 < X < 9)$?

Question ID: 0101576585

Suppose that $X$ follows a hypergeometric distribution with $N = 80$, $M = 21$, and $n = 14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(7 < X < 9)$?

Question ID: 0056052921

Suppose that $X$ follows a hypergeometric distribution with $N = 23$, $M = 7$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X < 2)$?

Question ID: 0426696270

Suppose that $X$ follows a hypergeometric distribution with $N = 59$, $M = 38$, and $n = 9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(9 < X < 13)$?

Question ID: 0350206425

Suppose that $X$ follows a hypergeometric distribution with $N = 40$, $M = 18$, and $n = 12$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(4 < X < 8)$?

Question ID: 0785390501

Suppose that $X$ follows a hypergeometric distribution with $N = 11$, $M = 5$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 5)$?

Question ID: 0263732938

Suppose that $X$ follows a hypergeometric distribution with $N = 33$, $M = 12$, and $n = 11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(4 < X < 8)$?

Question ID: 0376005548

Suppose that $X$ follows a hypergeometric distribution with $N = 62$, $M = 45$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 4)$?

Question ID: 0713714282

Suppose that $X$ follows a hypergeometric distribution with $N = 13$, $M = 8$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 3)$?

Question ID: 0849499237

Suppose that $X$ follows a hypergeometric distribution with $N = 39$, $M = 14$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X < 6)$?

Question ID: 0011505456

Suppose that $X$ follows a hypergeometric distribution with $N = 76$, $M = 53$, and $n = 6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(5 < X < 9)$?

Question ID: 0107035868

Suppose that $X$ follows a hypergeometric distribution with $N = 10$, $M = 6$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 3)$?

Question ID: 0738118979

Suppose that $X$ follows a hypergeometric distribution with $N = 100$, $M = 56$, and $n = 26$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 16)$?
What is $P(12 < X < 15)$?

Question ID: 0163382474

Suppose that $X$ follows a hypergeometric distribution with $N = 36$, $M = 21$, and $n = 14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(6 < X < 8)$?

Question ID: 0153346648

Suppose that $X$ follows a hypergeometric distribution with $N = 49$, $M = 21$, and $n = 7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 4)$?

Question ID: 0387871012

Suppose that $X$ follows a hypergeometric distribution with $N = 18$, $M = 10$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 2)$?

Question ID: 0536185810

Suppose that $X$ follows a hypergeometric distribution with $N = 93$, $M = 54$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(13 < X < 17)$?

Question ID: 0851977228

Suppose that $X$ follows a hypergeometric distribution with $N = 30$, $M = 17$, and $n = 10$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(6 < X < 9)$?

Question ID: 0206959029

Suppose that $X$ follows a hypergeometric distribution with $N = 70$, $M = 23$, and $n = 22$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(3 < X < 7)$?

Question ID: 0450918923

Suppose that $X$ follows a hypergeometric distribution with $N = 82$, $M = 40$, and $n = 37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(21 < X < 23)$?

Question ID: 0431889942

Suppose that $X$ follows a hypergeometric distribution with $N = 46$, $M = 28$, and $n = 7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(2 < X < 4)$?

Question ID: 0924765918

Suppose that $X$ follows a hypergeometric distribution with $N = 43$, $M = 12$, and $n = 11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(2 < X < 5)$?

Question ID: 0480595545

Suppose that $X$ follows a hypergeometric distribution with $N = 100$, $M = 46$, and $n = 15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 9)$?
What is $P(5 < X < 7)$?

Question ID: 0628276109

Suppose that $X$ follows a hypergeometric distribution with $N = 54$, $M = 20$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(9 < X < 12)$?

Question ID: 0306891759

Suppose that $X$ follows a hypergeometric distribution with $N = 52$, $M = 32$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(13 < X < 16)$?

Question ID: 0360824829

Suppose that $X$ follows a hypergeometric distribution with $N = 36$, $M = 9$, and $n = 9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(3 < X < 6)$?

Question ID: 0668663395

Suppose that $X$ follows a hypergeometric distribution with $N = 47$, $M = 12$, and $n = 10$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 < X < 7)$?

Question ID: 0948143357

Suppose that $X$ follows a hypergeometric distribution with $N = 14$, $M = 4$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 5)$?

Question ID: 0169792024

Suppose that $X$ follows a hypergeometric distribution with $N = 29$, $M = 19$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 < X < 5)$?

Question ID: 0760786338

Suppose that $X$ follows a hypergeometric distribution with $N = 91$, $M = 23$, and $n = 13$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X < 3)$?

Question ID: 0554146546

Suppose that $X$ follows a hypergeometric distribution with $N = 90$, $M = 55$, and $n = 31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 24)$?
What is $P(20 < X < 23)$?

Question ID: 0624005535

Suppose that $X$ follows a hypergeometric distribution with $N = 19$, $M = 11$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 4)$?

Question ID: 0188604870

Suppose that $X$ follows a hypergeometric distribution with $N = 93$, $M = 39$, and $n = 38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(15 < X < 18)$?

Question ID: 0416703302

Suppose that $X$ follows a hypergeometric distribution with $N = 78$, $M = 42$, and $n = 15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(4 < X < 8)$?

Question ID: 0706403095

Suppose that $X$ follows a hypergeometric distribution with $N = 65$, $M = 24$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(8 < X < 12)$?

Question ID: 0018775288

Suppose that $X$ follows a hypergeometric distribution with $N = 64$, $M = 18$, and $n = 18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 4)$?

Question ID: 0483013725

Suppose that $X$ follows a hypergeometric distribution with $N = 10$, $M = 5$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X < 4)$?

Question ID: 0148893902

Suppose that $X$ follows a hypergeometric distribution with $N = 96$, $M = 44$, and $n = 11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(5 < X < 8)$?

Question ID: 0373643699

Suppose that $X$ follows a hypergeometric distribution with $N = 84$, $M = 59$, and $n = 14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(11 < X < 13)$?

Question ID: 0332925293

Suppose that $X$ follows a hypergeometric distribution with $N = 26$, $M = 19$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(5 < X < 8)$?

Question ID: 0379238441

Suppose that $X$ follows a hypergeometric distribution with $N = 13$, $M = 6$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 5)$?

Question ID: 0123795565

Suppose that $X$ follows a hypergeometric distribution with $N = 57$, $M = 34$, and $n = 20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(13 < X < 17)$?

Question ID: 0266902250

Suppose that $X$ follows a hypergeometric distribution with $N = 27$, $M = 15$, and $n = 7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(3 < X < 6)$?

Question ID: 0312373828

Suppose that $X$ follows a hypergeometric distribution with $N = 93$, $M = 31$, and $n = 12$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(3 < X < 6)$?

Question ID: 0965908031

Suppose that $X$ follows a hypergeometric distribution with $N = 59$, $M = 25$, and $n = 8$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(2 < X < 6)$?

Question ID: 0822285497

Suppose that $X$ follows a hypergeometric distribution with $N = 54$, $M = 19$, and $n = 16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(5 < X < 7)$?

Question ID: 0336571776

Suppose that $X$ follows a hypergeometric distribution with $N = 67$, $M = 40$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(4 < X < 6)$?

Question ID: 0955009333

Suppose that $X$ follows a hypergeometric distribution with $N = 19$, $M = 7$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(2 < X < 6)$?

Question ID: 0220290379

Suppose that $X$ follows a hypergeometric distribution with $N = 21$, $M = 11$, and $n = 10$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(3 < X < 6)$?

Question ID: 0972193937

Suppose that $X$ follows a hypergeometric distribution with $N = 24$, $M = 9$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 5)$?

Question ID: 0229118161

Suppose that $X$ follows a hypergeometric distribution with $N = 95$, $M = 42$, and $n = 27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(14 < X < 18)$?

Question ID: 0453269139

Suppose that $X$ follows a hypergeometric distribution with $N = 97$, $M = 55$, and $n = 19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(13 < X < 17)$?

Question ID: 0134087908

Suppose that $X$ follows a hypergeometric distribution with $N = 42$, $M = 17$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(2 < X < 4)$?

Question ID: 0420243457

Suppose that $X$ follows a hypergeometric distribution with $N = 55$, $M = 24$, and $n = 18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(7 < X < 9)$?

Question ID: 0483978905

Suppose that $X$ follows a hypergeometric distribution with $N = 81$, $M = 41$, and $n = 31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 18)$?
What is $P(18 < X < 21)$?

Question ID: 0185819673

Suppose that $X$ follows a hypergeometric distribution with $N = 21$, $M = 14$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(2 < X < 4)$?

Question ID: 0782520633

Suppose that $X$ follows a hypergeometric distribution with $N = 60$, $M = 21$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X < 2)$?

Question ID: 0350110715

Suppose that $X$ follows a hypergeometric distribution with $N = 53$, $M = 15$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X < 3)$?

Question ID: 0607360571

Suppose that $X$ follows a hypergeometric distribution with $N = 34$, $M = 13$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 4)$?

Question ID: 0869990841

Suppose that $X$ follows a hypergeometric distribution with $N = 71$, $M = 32$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X < 4)$?

Question ID: 0257890757

Suppose that $X$ follows a hypergeometric distribution with $N = 28$, $M = 15$, and $n = 2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(2 < X < 6)$?

Question ID: 0612294931

Suppose that $X$ follows a hypergeometric distribution with $N = 15$, $M = 9$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 6)$?

Question ID: 0709686152

Suppose that $X$ follows a hypergeometric distribution with $N = 60$, $M = 34$, and $n = 20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(12 < X < 14)$?

Question ID: 0237350641

Suppose that $X$ follows a hypergeometric distribution with $N = 39$, $M = 13$, and $n = 8$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(4 < X < 8)$?

Question ID: 0196507868

Suppose that $X$ follows a hypergeometric distribution with $N = 52$, $M = 33$, and $n = 15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 10)$?
What is $P(6 < X < 9)$?

Question ID: 0848041036

Suppose that $X$ follows a hypergeometric distribution with $N = 16$, $M = 7$, and $n = 6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(2 < X < 5)$?

Question ID: 0400515855

Suppose that $X$ follows a hypergeometric distribution with $N = 67$, $M = 28$, and $n = 27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(11 < X < 14)$?

Question ID: 0356684435

Suppose that $X$ follows a hypergeometric distribution with $N = 46$, $M = 22$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(1 < X < 4)$?

Question ID: 0138369195

Suppose that $X$ follows a hypergeometric distribution with $N = 63$, $M = 20$, and $n = 18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(6 < X < 10)$?

Question ID: 0512818645

Suppose that $X$ follows a hypergeometric distribution with $N = 38$, $M = 20$, and $n = 6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(6 < X < 10)$?

Question ID: 0895323968

Suppose that $X$ follows a hypergeometric distribution with $N = 12$, $M = 5$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 < X < 4)$?

Question ID: 0813421485

Suppose that $X$ follows a hypergeometric distribution with $N = 24$, $M = 10$, and $n = 4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(2 < X < 5)$?

Question ID: 0957381461

Suppose that $X$ follows a hypergeometric distribution with $N = 35$, $M = 15$, and $n = 8$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(4 < X < 7)$?

Question ID: 0937624114

Suppose that $X$ follows a hypergeometric distribution with $N = 19$, $M = 5$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(1 < X < 4)$?

Question ID: 0106563134

Suppose that $X$ follows a hypergeometric distribution with $N = 24$, $M = 14$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(2 < X < 4)$?

Question ID: 0740143949

Suppose that $X$ follows a hypergeometric distribution with $N = 19$, $M = 5$, and $n = 3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(1 < X < 5)$?

Question ID: 0129902437

Suppose that $X$ follows a hypergeometric distribution with $N = 93$, $M = 52$, and $n = 5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(5 < X < 8)$?

Question ID: 0282095264

Self Assessment 8.6

Suppose that $X$ follows a Poisson distribution with rate $33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(23 \leq X \leq 24)$?

Suppose that $X$ follows a Poisson distribution with rate $18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(13 \leq X \leq 15)$?

Suppose that $X$ follows a Poisson distribution with rate $48$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(41 \leq X \leq 42)$?

Suppose that $X$ follows a Poisson distribution with rate $12$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(11 \leq X \leq 14)$?

Suppose that $X$ follows a Poisson distribution with rate $44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 41)$?
What is $P(54 \leq X \leq 55)$?

Suppose that $X$ follows a Poisson distribution with rate $50$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(42 \leq X \leq 45)$?

Suppose that $X$ follows a Poisson distribution with rate $43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 50)$?
What is $P(44 \leq X \leq 46)$?

Suppose that $X$ follows a Poisson distribution with rate $40$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(50 \leq X \leq 51)$?

Suppose that $X$ follows a Poisson distribution with rate $15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(10 \leq X \leq 11)$?

Suppose that $X$ follows a Poisson distribution with rate $16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(24 \leq X \leq 28)$?

Suppose that $X$ follows a Poisson distribution with rate $43$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 33)$?
What is $P(36 \leq X \leq 37)$?

Suppose that $X$ follows a Poisson distribution with rate $9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 8)$?
What is $P(15 \leq X \leq 18)$?

Suppose that $X$ follows a Poisson distribution with rate $2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(6 \leq X \leq 8)$?

Suppose that $X$ follows a Poisson distribution with rate $14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 19)$?
What is $P(13 \leq X \leq 16)$?

Suppose that $X$ follows a Poisson distribution with rate $33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 40)$?
What is $P(27 \leq X \leq 29)$?

Suppose that $X$ follows a Poisson distribution with rate $50$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(49 \leq X \leq 53)$?

Suppose that $X$ follows a Poisson distribution with rate $1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(1 \leq X \leq 3)$?

Suppose that $X$ follows a Poisson distribution with rate $44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 45)$?
What is $P(54 \leq X \leq 57)$?

Suppose that $X$ follows a Poisson distribution with rate $4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(3 \leq X \leq 7)$?

Suppose that $X$ follows a Poisson distribution with rate $22$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 18)$?
What is $P(30 \leq X \leq 31)$?

Suppose that $X$ follows a Poisson distribution with rate $32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 40)$?
What is $P(38 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $21$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(21 \leq X \leq 23)$?

Suppose that $X$ follows a Poisson distribution with rate $33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 38)$?
What is $P(32 \leq X \leq 33)$?

Suppose that $X$ follows a Poisson distribution with rate $40$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 47)$?
What is $P(43 \leq X \leq 45)$?

Suppose that $X$ follows a Poisson distribution with rate $29$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 24)$?
What is $P(23 \leq X \leq 26)$?

Suppose that $X$ follows a Poisson distribution with rate $15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(13 \leq X \leq 14)$?

Suppose that $X$ follows a Poisson distribution with rate $20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(23 \leq X \leq 24)$?

Suppose that $X$ follows a Poisson distribution with rate $18$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 12)$?
What is $P(11 \leq X \leq 12)$?

Suppose that $X$ follows a Poisson distribution with rate $27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 31)$?
What is $P(36 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $29$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(37 \leq X \leq 40)$?

Suppose that $X$ follows a Poisson distribution with rate $27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(37 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $36$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 31)$?
What is $P(39 \leq X \leq 41)$?

Suppose that $X$ follows a Poisson distribution with rate $46$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 41)$?
What is $P(34 \leq X \leq 38)$?

Suppose that $X$ follows a Poisson distribution with rate $1$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(1 \leq X \leq 2)$?

Suppose that $X$ follows a Poisson distribution with rate $15$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 14)$?
What is $P(13 \leq X \leq 15)$?

Suppose that $X$ follows a Poisson distribution with rate $24$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(20 \leq X \leq 24)$?

Suppose that $X$ follows a Poisson distribution with rate $47$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 53)$?
What is $P(36 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $50$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 59)$?
What is $P(60 \leq X \leq 64)$?

Suppose that $X$ follows a Poisson distribution with rate $3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(7 \leq X \leq 10)$?

Suppose that $X$ follows a Poisson distribution with rate $30$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 30)$?
What is $P(20 \leq X \leq 23)$?

Suppose that $X$ follows a Poisson distribution with rate $19$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 15)$?
What is $P(18 \leq X \leq 21)$?

Suppose that $X$ follows a Poisson distribution with rate $2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 0)$?
What is $P(6 \leq X \leq 10)$?

Suppose that $X$ follows a Poisson distribution with rate $17$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(21 \leq X \leq 24)$?

Suppose that $X$ follows a Poisson distribution with rate $29$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 38)$?
What is $P(35 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $13$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(18 \leq X \leq 21)$?

Suppose that $X$ follows a Poisson distribution with rate $49$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 60)$?
What is $P(43 \leq X \leq 45)$?

Suppose that $X$ follows a Poisson distribution with rate $5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(5 \leq X \leq 8)$?

Suppose that $X$ follows a Poisson distribution with rate $3$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 4)$?
What is $P(0 \leq X \leq 1)$?

Suppose that $X$ follows a Poisson distribution with rate $30$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 21)$?
What is $P(23 \leq X \leq 24)$?

Suppose that $X$ follows a Poisson distribution with rate $11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 16)$?
What is $P(14 \leq X \leq 15)$?

Suppose that $X$ follows a Poisson distribution with rate $27$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(37 \leq X \leq 41)$?

Suppose that $X$ follows a Poisson distribution with rate $6$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 6)$?
What is $P(3 \leq X \leq 6)$?

Suppose that $X$ follows a Poisson distribution with rate $35$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 36)$?
What is $P(43 \leq X \leq 46)$?

Suppose that $X$ follows a Poisson distribution with rate $38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 37)$?
What is $P(42 \leq X \leq 44)$?

Suppose that $X$ follows a Poisson distribution with rate $38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 47)$?
What is $P(28 \leq X \leq 30)$?

Suppose that $X$ follows a Poisson distribution with rate $23$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 18)$?
What is $P(33 \leq X \leq 36)$?

Suppose that $X$ follows a Poisson distribution with rate $4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(9 \leq X \leq 12)$?

Suppose that $X$ follows a Poisson distribution with rate $34$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 29)$?
What is $P(44 \leq X \leq 46)$?

Suppose that $X$ follows a Poisson distribution with rate $20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(29 \leq X \leq 30)$?

Suppose that $X$ follows a Poisson distribution with rate $23$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 25)$?
What is $P(29 \leq X \leq 33)$?

Suppose that $X$ follows a Poisson distribution with rate $16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(20 \leq X \leq 21)$?

Suppose that $X$ follows a Poisson distribution with rate $38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 32)$?
What is $P(31 \leq X \leq 32)$?

Suppose that $X$ follows a Poisson distribution with rate $16$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(22 \leq X \leq 23)$?

Suppose that $X$ follows a Poisson distribution with rate $50$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 48)$?
What is $P(38 \leq X \leq 42)$?

Suppose that $X$ follows a Poisson distribution with rate $44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(41 \leq X \leq 45)$?

Suppose that $X$ follows a Poisson distribution with rate $17$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(10 \leq X \leq 13)$?

Suppose that $X$ follows a Poisson distribution with rate $13$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(8 \leq X \leq 10)$?

Suppose that $X$ follows a Poisson distribution with rate $47$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 48)$?
What is $P(45 \leq X \leq 49)$?

Suppose that $X$ follows a Poisson distribution with rate $47$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 38)$?
What is $P(46 \leq X \leq 49)$?

Suppose that $X$ follows a Poisson distribution with rate $33$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 29)$?
What is $P(37 \leq X \leq 41)$?

Suppose that $X$ follows a Poisson distribution with rate $32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(42 \leq X \leq 45)$?

Suppose that $X$ follows a Poisson distribution with rate $2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 1)$?
What is $P(6 \leq X \leq 8)$?

Suppose that $X$ follows a Poisson distribution with rate $11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(15 \leq X \leq 19)$?

Suppose that $X$ follows a Poisson distribution with rate $36$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(32 \leq X \leq 36)$?

Suppose that $X$ follows a Poisson distribution with rate $5$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 2)$?
What is $P(9 \leq X \leq 11)$?

Suppose that $X$ follows a Poisson distribution with rate $32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 23)$?
What is $P(35 \leq X \leq 37)$?

Suppose that $X$ follows a Poisson distribution with rate $2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(4 \leq X \leq 8)$?

Suppose that $X$ follows a Poisson distribution with rate $34$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 39)$?
What is $P(39 \leq X \leq 40)$?

Suppose that $X$ follows a Poisson distribution with rate $39$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(31 \leq X \leq 35)$?

Suppose that $X$ follows a Poisson distribution with rate $11$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(14 \leq X \leq 17)$?

Suppose that $X$ follows a Poisson distribution with rate $17$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 17)$?
What is $P(20 \leq X \leq 23)$?

Suppose that $X$ follows a Poisson distribution with rate $7$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 11)$?
What is $P(2 \leq X \leq 5)$?

Suppose that $X$ follows a Poisson distribution with rate $31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 27)$?
What is $P(36 \leq X \leq 39)$?

Suppose that $X$ follows a Poisson distribution with rate $39$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 40)$?
What is $P(35 \leq X \leq 38)$?

Suppose that $X$ follows a Poisson distribution with rate $20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(24 \leq X \leq 27)$?

Suppose that $X$ follows a Poisson distribution with rate $34$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 33)$?
What is $P(25 \leq X \leq 29)$?

Suppose that $X$ follows a Poisson distribution with rate $42$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 52)$?
What is $P(48 \leq X \leq 50)$?

Suppose that $X$ follows a Poisson distribution with rate $31$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(33 \leq X \leq 35)$?

Suppose that $X$ follows a Poisson distribution with rate $20$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(28 \leq X \leq 32)$?

Suppose that $X$ follows a Poisson distribution with rate $4$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 7)$?
What is $P(8 \leq X \leq 12)$?

Suppose that $X$ follows a Poisson distribution with rate $40$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 33)$?
What is $P(39 \leq X \leq 41)$?

Suppose that $X$ follows a Poisson distribution with rate $38$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 27)$?
What is $P(34 \leq X \leq 35)$?

Suppose that $X$ follows a Poisson distribution with rate $9$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 3)$?
What is $P(12 \leq X \leq 16)$?

Suppose that $X$ follows a Poisson distribution with rate $44$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 41)$?
What is $P(50 \leq X \leq 54)$?

Suppose that $X$ follows a Poisson distribution with rate $32$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 34)$?
What is $P(30 \leq X \leq 34)$?

Suppose that $X$ follows a Poisson distribution with rate $14$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 13)$?
What is $P(21 \leq X \leq 23)$?

Suppose that $X$ follows a Poisson distribution with rate $39$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 44)$?
What is $P(34 \leq X \leq 37)$?

Suppose that $X$ follows a Poisson distribution with rate $42$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 49)$?
What is $P(41 \leq X \leq 42)$?

Suppose that $X$ follows a Poisson distribution with rate $2$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 5)$?
What is $P(3 \leq X \leq 7)$?

Suppose that $X$ follows a Poisson distribution with rate $37$.

What is $E[X]$?
What is $\text{var}(X)$?
What is $P(X = 26)$?
What is $P(31 \leq X \leq 35)$?

Self Assessment 8.7

A fair 15-sided die is tossed 92 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 < v \leq 10$?
Across the 92 tosses, what is the probability of observing a value as in (a) exactly 19 times?

Question ID: 0417214007

A fair 9-sided die is tossed 44 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v \leq 4$?
Across the 44 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0081094632

A fair 8-sided die is tossed 76 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 4$?
Across the 76 tosses, what is the probability of observing a value as in (a) exactly 29 times?

Question ID: 0205144413

A fair 16-sided die is tossed 47 times.

On any single toss, what is the probability of observing a value, $v$, such that $5 \leq v \leq 10$?
Across the 47 tosses, what is the probability of observing a value as in (a) exactly 18 times?

Question ID: 0642022771

A fair 16-sided die is tossed 17 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 < v < 13$?
Across the 17 tosses, what is the probability of never observing a value as in (a)?

Question ID: 0667463688

A fair 16-sided die is tossed 82 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 6$?
Across the 82 tosses, what is the probability of observing a value as in (a) exactly 26 times?

Question ID: 0532902750

A fair 12-sided die is tossed 53 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v < 7$?
Across the 53 tosses, what is the probability of observing a value as in (a) exactly 23 times?

Question ID: 0422048940

A fair 13-sided die is tossed 82 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 \leq v \leq 8$?
Across the 82 tosses, what is the probability of observing a value as in (a) exactly 32 times?

Question ID: 0547579686

A fair 13-sided die is tossed 38 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 \leq v < 11$?
Across the 38 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0900334229

A fair 18-sided die is tossed 66 times.

On any single toss, what is the probability of observing a value, $v$, such that $8 \leq v < 11$?
Across the 66 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0803276024

A fair 20-sided die is tossed 46 times.

On any single toss, what is the probability of observing a value, $v$, such that $14 \leq v \leq 19$?
Across the 46 tosses, what is the probability of observing a value as in (a) exactly 15 times?

Question ID: 0858807238

A fair 11-sided die is tossed 25 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 \leq v < 8$?
Across the 25 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0913943811

A fair 15-sided die is tossed 74 times.

On any single toss, what is the probability of observing a value, $v$, such that $10 \leq v < 14$?
Across the 74 tosses, what is the probability of observing a value as in (a) exactly 20 times?

Question ID: 0693653991

A fair 17-sided die is tossed 49 times.

On any single toss, what is the probability of observing a value, $v$, such that $11 \leq v < 15$?
Across the 49 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0839226734

A fair 12-sided die is tossed 98 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v \leq 5$?
Across the 98 tosses, what is the probability of observing a value as in (a) exactly 42 times?

Question ID: 0121192430

A fair 7-sided die is tossed 22 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 5$?
Across the 22 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0302727527

A fair 17-sided die is tossed 71 times.

On any single toss, what is the probability of observing a value, $v$, such that $12 \leq v < 16$?
Across the 71 tosses, what is the probability of observing a value as in (a) exactly 17 times?

Question ID: 0107258263

A fair 11-sided die is tossed 59 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 < v \leq 9$?
Across the 59 tosses, what is the probability of observing a value as in (a) exactly 28 times?

Question ID: 0141564763

A fair 13-sided die is tossed 76 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 6$?
Across the 76 tosses, what is the probability of observing a value as in (a) exactly 30 times?

Question ID: 0261465179

A fair 16-sided die is tossed 39 times.

On any single toss, what is the probability of observing a value, $v$, such that $11 < v < 15$?
Across the 39 tosses, what is the probability of observing a value as in (a) exactly 8 times?

Question ID: 0931870521

A fair 16-sided die is tossed 42 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v \leq 8$?
Across the 42 tosses, what is the probability of observing a value as in (a) exactly 9 times?

Question ID: 0161225658

A fair 10-sided die is tossed 79 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v \leq 4$?
Across the 79 tosses, what is the probability of observing a value as in (a) exactly 32 times?

Question ID: 0140550477

A fair 7-sided die is tossed 32 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v < 5$?
Across the 32 tosses, what is the probability of observing a value as in (a) exactly 19 times?

Question ID: 0316171322

A fair 8-sided die is tossed 43 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 6$?
Across the 43 tosses, what is the probability of observing a value as in (a) exactly 28 times?

Question ID: 0460508673

A fair 12-sided die is tossed 82 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 < v \leq 9$?
Across the 82 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0045004593

A fair 6-sided die is tossed 61 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v < 3$?
Across the 61 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0264139457

A fair 18-sided die is tossed 48 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v < 6$?
Across the 48 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0551283827

A fair 6-sided die is tossed 12 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v < 5$?
Across the 12 tosses, what is the probability of observing a value as in (a) exactly 7 times?

Question ID: 0686088684

A fair 16-sided die is tossed 76 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v \leq 4$?
Across the 76 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0955677572

A fair 15-sided die is tossed 23 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v \leq 11$?
Across the 23 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0628180213

A fair 17-sided die is tossed 91 times.

On any single toss, what is the probability of observing a value, $v$, such that $12 \leq v \leq 17$?
Across the 91 tosses, what is the probability of observing a value as in (a) exactly 33 times?

Question ID: 0216081161

A fair 12-sided die is tossed 100 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 < v \leq 6$?
Across the 100 tosses, what is the probability of observing a value as in (a) exactly 26 times?

Question ID: 0015626625

A fair 14-sided die is tossed 92 times.

On any single toss, what is the probability of observing a value, $v$, such that $8 \leq v \leq 12$?
Across the 92 tosses, what is the probability of observing a value as in (a) exactly 34 times?

Question ID: 0922106680

A fair 15-sided die is tossed 38 times.

On any single toss, what is the probability of observing a value, $v$, such that $8 \leq v < 12$?
Across the 38 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0288112349

A fair 11-sided die is tossed 80 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 < v < 5$?
Across the 80 tosses, what is the probability of observing a value as in (a) exactly 8 times?

Question ID: 0059518289

A fair 6-sided die is tossed 70 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 5$?
Across the 70 tosses, what is the probability of observing a value as in (a) exactly 48 times?

Question ID: 0666529693

A fair 8-sided die is tossed 17 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v < 5$?
Across the 17 tosses, what is the probability of observing a value as in (a) exactly 5 times?

Question ID: 0594302518

A fair 7-sided die is tossed 16 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v < 5$?
Across the 16 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0003342600

A fair 14-sided die is tossed 86 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v \leq 5$?
Across the 86 tosses, what is the probability of observing a value as in (a) exactly 32 times?

Question ID: 0427355898

A fair 7-sided die is tossed 85 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v \leq 7$?
Across the 85 tosses, what is the probability of observing a value as in (a) exactly 62 times?

Question ID: 0497283984

A fair 10-sided die is tossed 67 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v \leq 4$?
Across the 67 tosses, what is the probability of observing a value as in (a) exactly 21 times?

Question ID: 0429824949

A fair 7-sided die is tossed 60 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v \leq 6$?
Across the 60 tosses, what is the probability of observing a value as in (a) exactly 44 times?

Question ID: 0603371337

A fair 20-sided die is tossed 73 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 < v < 10$?
Across the 73 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0826955662

A fair 17-sided die is tossed 12 times.

On any single toss, what is the probability of observing a value, $v$, such that $10 \leq v \leq 12$?
Across the 12 tosses, what is the probability of observing a value as in (a) at least once?

Question ID: 0750396094

A fair 8-sided die is tossed 38 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v < 3$?
Across the 38 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0362113838

A fair 6-sided die is tossed 39 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 3$?
Across the 39 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0803522120

A fair 10-sided die is tossed 76 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v < 8$?
Across the 76 tosses, what is the probability of observing a value as in (a) exactly 39 times?

Question ID: 0933171266

A fair 20-sided die is tossed 23 times.

On any single toss, what is the probability of observing a value, $v$, such that $5 \leq v < 10$?
Across the 23 tosses, what is the probability of observing a value as in (a) exactly 6 times?

Question ID: 0482636780

A fair 13-sided die is tossed 21 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v < 6$?
Across the 21 tosses, what is the probability of observing a value as in (a) exactly 6 times?

Question ID: 0356662312

A fair 10-sided die is tossed 23 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 3$?
Across the 23 tosses, what is the probability of observing a value as in (a) exactly 5 times?

Question ID: 0032252904

A fair 19-sided die is tossed 40 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 < v \leq 8$?
Across the 40 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0326504774

A fair 7-sided die is tossed 80 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v < 4$?
Across the 80 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0140596121

A fair 15-sided die is tossed 50 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 < v < 8$?
Across the 50 tosses, what is the probability of observing a value as in (a) at least once?

Question ID: 0175209299

A fair 10-sided die is tossed 78 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v < 5$?
Across the 78 tosses, what is the probability of observing a value as in (a) exactly 24 times?

Question ID: 0448251908

A fair 13-sided die is tossed 22 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 \leq v < 11$?
Across the 22 tosses, what is the probability of observing a value as in (a) exactly 8 times?

Question ID: 0183124685

A fair 15-sided die is tossed 57 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v < 5$?
Across the 57 tosses, what is the probability of observing a value as in (a) exactly 16 times?

Question ID: 0823514015

A fair 18-sided die is tossed 59 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v \leq 7$?
Across the 59 tosses, what is the probability of observing a value as in (a) exactly 17 times?

Question ID: 0228581056

A fair 16-sided die is tossed 80 times.

On any single toss, what is the probability of observing a value, $v$, such that $11 < v \leq 14$?
Across the 80 tosses, what is the probability of observing a value as in (a) exactly 16 times?

Question ID: 0990846844

A fair 16-sided die is tossed 40 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 < v \leq 10$?
Across the 40 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0262177161

A fair 10-sided die is tossed 95 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 \leq v < 9$?
Across the 95 tosses, what is the probability of observing a value as in (a) exactly 48 times?

Question ID: 0807478256

A fair 16-sided die is tossed 11 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 < v < 13$?
Across the 11 tosses, what is the probability of observing a value as in (a) at least once?

Question ID: 0988860440

A fair 12-sided die is tossed 26 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 4$?
Across the 26 tosses, what is the probability of observing a value as in (a) exactly 7 times?

Question ID: 0891926558

A fair 15-sided die is tossed 48 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 < v < 12$?
Across the 48 tosses, what is the probability of observing a value as in (a) exactly 7 times?

Question ID: 0518549594

A fair 13-sided die is tossed 85 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v \leq 8$?
Across the 85 tosses, what is the probability of observing a value as in (a) exactly 20 times?

Question ID: 0181277460

A fair 16-sided die is tossed 88 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 \leq v < 11$?
Across the 88 tosses, what is the probability of observing a value as in (a) exactly 12 times?

Question ID: 0573394124

A fair 19-sided die is tossed 24 times.

On any single toss, what is the probability of observing a value, $v$, such that $12 < v \leq 15$?
Across the 24 tosses, what is the probability of never observing a value as in (a)?

Question ID: 0374879895

A fair 18-sided die is tossed 30 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v < 10$?
Across the 30 tosses, what is the probability of observing a value as in (a) exactly 7 times?

Question ID: 0595347243

A fair 11-sided die is tossed 97 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v \leq 7$?
Across the 97 tosses, what is the probability of observing a value as in (a) exactly 45 times?

Question ID: 0939003683

A fair 15-sided die is tossed 66 times.

On any single toss, what is the probability of observing a value, $v$, such that $10 < v < 14$?
Across the 66 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0286793454

A fair 18-sided die is tossed 94 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v < 4$?
Across the 94 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0572908574

A fair 8-sided die is tossed 50 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v < 5$?
Across the 50 tosses, what is the probability of observing a value as in (a) exactly 20 times?

Question ID: 0084616907

A fair 14-sided die is tossed 64 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v \leq 6$?
Across the 64 tosses, what is the probability of observing a value as in (a) exactly 24 times?

Question ID: 0195856813

A fair 13-sided die is tossed 48 times.

On any single toss, what is the probability of observing a value, $v$, such that $5 \leq v < 10$?
Across the 48 tosses, what is the probability of observing a value as in (a) exactly 19 times?

Question ID: 0129614817

A fair 13-sided die is tossed 40 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v < 6$?
Across the 40 tosses, what is the probability of observing a value as in (a) exactly 13 times?

Question ID: 0172565262

A fair 9-sided die is tossed 23 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v < 6$?
Across the 23 tosses, what is the probability of observing a value as in (a) exactly 8 times?

Question ID: 0295990561

A fair 20-sided die is tossed 30 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 \leq v < 9$?
Across the 30 tosses, what is the probability of observing a value as in (a) exactly 8 times?

Question ID: 0527694928

A fair 8-sided die is tossed 33 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v < 6$?
Across the 33 tosses, what is the probability of observing a value as in (a) exactly 13 times?

Question ID: 0406013669

A fair 11-sided die is tossed 73 times.

On any single toss, what is the probability of observing a value, $v$, such that $5 < v < 8$?
Across the 73 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0996288581

A fair 14-sided die is tossed 49 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v \leq 11$?
Across the 49 tosses, what is the probability of observing a value as in (a) exactly 22 times?

Question ID: 0586658047

A fair 6-sided die is tossed 89 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v \leq 3$?
Across the 89 tosses, what is the probability of observing a value as in (a) exactly 46 times?

Question ID: 0491664348

A fair 14-sided die is tossed 37 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 \leq v \leq 11$?
Across the 37 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0409654100

A fair 12-sided die is tossed 71 times.

On any single toss, what is the probability of observing a value, $v$, such that $5 < v \leq 9$?
Across the 71 tosses, what is the probability of observing a value as in (a) exactly 24 times?

Question ID: 0124711488

A fair 13-sided die is tossed 61 times.

On any single toss, what is the probability of observing a value, $v$, such that $7 \leq v < 11$?
Across the 61 tosses, what is the probability of observing a value as in (a) exactly 20 times?

Question ID: 0579985501

A fair 9-sided die is tossed 42 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v \leq 6$?
Across the 42 tosses, what is the probability of observing a value as in (a) exactly 24 times?

Question ID: 0486300123

A fair 7-sided die is tossed 31 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 \leq v < 5$?
Across the 31 tosses, what is the probability of observing a value as in (a) exactly 19 times?

Question ID: 0774227217

A fair 13-sided die is tossed 33 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 < v \leq 9$?
Across the 33 tosses, what is the probability of observing a value as in (a) exactly 14 times?

Question ID: 0499821845

A fair 15-sided die is tossed 68 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v < 11$?
Across the 68 tosses, what is the probability of observing a value as in (a) exactly 23 times?

Question ID: 0769492587

A fair 8-sided die is tossed 62 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v < 7$?
Across the 62 tosses, what is the probability of observing a value as in (a) exactly 32 times?

Question ID: 0938949787

A fair 10-sided die is tossed 12 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v \leq 5$?
Across the 12 tosses, what is the probability of never observing a value as in (a)?

Question ID: 0813124173

A fair 19-sided die is tossed 94 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v < 5$?
Across the 94 tosses, what is the probability of observing a value as in (a) exactly 10 times?

Question ID: 0355503837

A fair 12-sided die is tossed 62 times.

On any single toss, what is the probability of observing a value, $v$, such that $6 \leq v < 8$?
Across the 62 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0203041689

A fair 20-sided die is tossed 81 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 < v < 12$?
Across the 81 tosses, what is the probability of observing a value as in (a) exactly 9 times?

Question ID: 0342886374

A fair 7-sided die is tossed 23 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 < v \leq 4$?
Across the 23 tosses, what is the probability of observing a value as in (a) exactly 7 times?

Question ID: 0214523842

A fair 20-sided die is tossed 50 times.

On any single toss, what is the probability of observing a value, $v$, such that $9 \leq v \leq 14$?
Across the 50 tosses, what is the probability of observing a value as in (a) exactly 16 times?

Question ID: 0823589318

A fair 20-sided die is tossed 10 times.

On any single toss, what is the probability of observing a value, $v$, such that $12 \leq v < 17$?
Across the 10 tosses, what is the probability of observing a value as in (a) at least once?

Question ID: 0774857677

A fair 18-sided die is tossed 29 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 \leq v \leq 7$?
Across the 29 tosses, what is the probability of observing a value as in (a) exactly 9 times?

Question ID: 0361701113

A fair 17-sided die is tossed 59 times.

On any single toss, what is the probability of observing a value, $v$, such that $4 < v < 8$?
Across the 59 tosses, what is the probability of observing a value as in (a) exactly 11 times?

Question ID: 0750371531

A fair 16-sided die is tossed 96 times.

On any single toss, what is the probability of observing a value, $v$, such that $2 \leq v \leq 4$?
Across the 96 tosses, what is the probability of observing a value as in (a) exactly 19 times?

Question ID: 0996756825

A fair 6-sided die is tossed 35 times.

On any single toss, what is the probability of observing a value, $v$, such that $1 < v < 6$?
Across the 35 tosses, what is the probability of observing a value as in (a) exactly 24 times?

Question ID: 0853541574

A fair 12-sided die is tossed 25 times.

On any single toss, what is the probability of observing a value, $v$, such that $3 < v \leq 5$?
Across the 25 tosses, what is the probability of observing a value as in (a) at least once?

Question ID: 0033744215

Self Assessment 8.8

There are a total of 77 phones currently at a local repair shop. Of these, 29 phones have a cracked display. Suppose that 25 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 11 phones have a cracked display?

Question ID: 0650205448

There are a total of 67 cars currently at a local garage. Of these, 31 cars have a cracked windshield. Suppose that 21 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 9 cars have a cracked windshield?

Question ID: 0601991924

There are a total of 28 cars currently at a local garage. Of these, 26 cars have a cracked windshield. Suppose that 1 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 0 cars have a cracked windshield?

Question ID: 0245206344

There are a total of 26 computers currently at a local repair shop. Of these, 15 computers have a broken screen. Suppose that 7 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 2 computers have a broken screen?

Question ID: 0856187379

There are a total of 97 cars currently at a local garage. Of these, 28 cars have a cracked windshield. Suppose that 3 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 1 cars have a cracked windshield?

Question ID: 0843523522

There are a total of 83 computers currently at a local repair shop. Of these, 81 computers have a broken screen. Suppose that 2 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 1 computers have a broken screen?

Question ID: 0142037858

There are a total of 90 cameras currently at a local repair shop. Of these, 72 cameras have a broken lens. Suppose that 16 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 10 cameras have a broken lens?

Question ID: 0979747383

There are a total of 69 patients currently at a local clinic. Of these, 8 patients have flu-like symptoms. Suppose that 6 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 2 patients have flu-like symptoms?

Question ID: 0728639879

There are a total of 85 patients currently at a local clinic. Of these, 12 patients have flu-like symptoms. Suppose that 7 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0933901976

There are a total of 43 cars currently at a local garage. Of these, 31 cars have a cracked windshield. Suppose that 10 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 6 cars have a cracked windshield?

Question ID: 0652890131

There are a total of 96 patients currently at a local clinic. Of these, 64 patients have flu-like symptoms. Suppose that 12 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 10 patients have flu-like symptoms?

Question ID: 0476206666

There are a total of 92 patients currently at a local clinic. Of these, 82 patients have flu-like symptoms. Suppose that 8 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 6 patients have flu-like symptoms?

Question ID: 0324027255

There are a total of 70 cameras currently at a local repair shop. Of these, 22 cameras have a broken lens. Suppose that 7 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 1 cameras have a broken lens?

Question ID: 0616022891

There are a total of 49 cars currently at a local garage. Of these, 5 cars have a cracked windshield. Suppose that 5 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 2 cars have a cracked windshield?

Question ID: 0206638811

There are a total of 65 computers currently at a local repair shop. Of these, 61 computers have a broken screen. Suppose that 4 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 4 computers have a broken screen?

Question ID: 0916492786

There are a total of 71 cameras currently at a local repair shop. Of these, 39 cameras have a broken lens. Suppose that 6 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 4 cameras have a broken lens?

Question ID: 0547981649

There are a total of 45 patients currently at a local clinic. Of these, 31 patients have flu-like symptoms. Suppose that 7 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 6 patients have flu-like symptoms?

Question ID: 0550329535

There are a total of 25 cameras currently at a local repair shop. Of these, 6 cameras have a broken lens. Suppose that 3 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0891811403

There are a total of 96 phones currently at a local repair shop. Of these, 2 phones have a cracked display. Suppose that 2 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 1 phones have a cracked display?

Question ID: 0019924910

There are a total of 57 cars currently at a local garage. Of these, 44 cars have a cracked windshield. Suppose that 8 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 7 cars have a cracked windshield?

Question ID: 0137218567

There are a total of 64 cameras currently at a local repair shop. Of these, 55 cameras have a broken lens. Suppose that 5 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 5 cameras have a broken lens?

Question ID: 0618279346

There are a total of 90 phones currently at a local repair shop. Of these, 77 phones have a cracked display. Suppose that 8 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 5 phones have a cracked display?

Question ID: 0495991017

There are a total of 44 phones currently at a local repair shop. Of these, 31 phones have a cracked display. Suppose that 6 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 4 phones have a cracked display?

Question ID: 0966031396

There are a total of 26 computers currently at a local repair shop. Of these, 8 computers have a broken screen. Suppose that 8 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 0 computers have a broken screen?

Question ID: 0508231630

There are a total of 35 patients currently at a local clinic. Of these, 9 patients have flu-like symptoms. Suppose that 5 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 0 patients have flu-like symptoms?

Question ID: 0000490591

There are a total of 30 cameras currently at a local repair shop. Of these, 25 cameras have a broken lens. Suppose that 2 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0881975406

There are a total of 93 cameras currently at a local repair shop. Of these, 85 cameras have a broken lens. Suppose that 8 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 8 cameras have a broken lens?

Question ID: 0575912791

There are a total of 22 phones currently at a local repair shop. Of these, 19 phones have a cracked display. Suppose that 3 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 3 phones have a cracked display?

Question ID: 0563060613

There are a total of 87 patients currently at a local clinic. Of these, 3 patients have flu-like symptoms. Suppose that 3 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0495265834

There are a total of 71 cameras currently at a local repair shop. Of these, 4 cameras have a broken lens. Suppose that 2 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 1 cameras have a broken lens?

Question ID: 0031145083

There are a total of 43 computers currently at a local repair shop. Of these, 5 computers have a broken screen. Suppose that 3 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 1 computers have a broken screen?

Question ID: 0562709673

There are a total of 22 computers currently at a local repair shop. Of these, 6 computers have a broken screen. Suppose that 6 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 3 computers have a broken screen?

Question ID: 0431933076

There are a total of 40 patients currently at a local clinic. Of these, 3 patients have flu-like symptoms. Suppose that 2 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0591295082

There are a total of 74 cameras currently at a local repair shop. Of these, 54 cameras have a broken lens. Suppose that 3 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0210119358

There are a total of 83 patients currently at a local clinic. Of these, 11 patients have flu-like symptoms. Suppose that 8 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 3 patients have flu-like symptoms?

Question ID: 0356867696

There are a total of 36 cameras currently at a local repair shop. Of these, 10 cameras have a broken lens. Suppose that 3 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0609979867

There are a total of 67 cameras currently at a local repair shop. Of these, 39 cameras have a broken lens. Suppose that 26 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 17 cameras have a broken lens?

Question ID: 0375608111

There are a total of 79 cars currently at a local garage. Of these, 49 cars have a cracked windshield. Suppose that 11 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 9 cars have a cracked windshield?

Question ID: 0555928450

There are a total of 23 patients currently at a local clinic. Of these, 19 patients have flu-like symptoms. Suppose that 4 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 3 patients have flu-like symptoms?

Question ID: 0919753890

There are a total of 61 cars currently at a local garage. Of these, 43 cars have a cracked windshield. Suppose that 5 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 4 cars have a cracked windshield?

Question ID: 0105389157

There are a total of 55 computers currently at a local repair shop. Of these, 39 computers have a broken screen. Suppose that 13 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 6 computers have a broken screen?

Question ID: 0833682476

There are a total of 79 cars currently at a local garage. Of these, 49 cars have a cracked windshield. Suppose that 29 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 22 cars have a cracked windshield?

Question ID: 0568095355

There are a total of 65 cameras currently at a local repair shop. Of these, 29 cameras have a broken lens. Suppose that 23 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 6 cameras have a broken lens?

Question ID: 0693407635

There are a total of 47 cameras currently at a local repair shop. Of these, 10 cameras have a broken lens. Suppose that 3 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 0 cameras have a broken lens?

Question ID: 0733544972

There are a total of 23 cars currently at a local garage. Of these, 15 cars have a cracked windshield. Suppose that 3 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 2 cars have a cracked windshield?

Question ID: 0515786195

There are a total of 83 computers currently at a local repair shop. Of these, 27 computers have a broken screen. Suppose that 3 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 2 computers have a broken screen?

Question ID: 0046487817

There are a total of 79 patients currently at a local clinic. Of these, 5 patients have flu-like symptoms. Suppose that 2 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0599841984

There are a total of 68 phones currently at a local repair shop. Of these, 21 phones have a cracked display. Suppose that 2 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 0 phones have a cracked display?

Question ID: 0646257772

There are a total of 92 cars currently at a local garage. Of these, 88 cars have a cracked windshield. Suppose that 2 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 2 cars have a cracked windshield?

Question ID: 0087394255

There are a total of 52 computers currently at a local repair shop. Of these, 39 computers have a broken screen. Suppose that 11 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 8 computers have a broken screen?

Question ID: 0072066229

There are a total of 84 patients currently at a local clinic. Of these, 5 patients have flu-like symptoms. Suppose that 3 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 0 patients have flu-like symptoms?

Question ID: 0201729078

There are a total of 69 cars currently at a local garage. Of these, 27 cars have a cracked windshield. Suppose that 4 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 0 cars have a cracked windshield?

Question ID: 0181941828

There are a total of 64 computers currently at a local repair shop. Of these, 18 computers have a broken screen. Suppose that 9 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 3 computers have a broken screen?

Question ID: 0955463348

There are a total of 52 patients currently at a local clinic. Of these, 35 patients have flu-like symptoms. Suppose that 15 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 13 patients have flu-like symptoms?

Question ID: 0537369987

There are a total of 53 cameras currently at a local repair shop. Of these, 17 cameras have a broken lens. Suppose that 11 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0088190955

There are a total of 89 cars currently at a local garage. Of these, 42 cars have a cracked windshield. Suppose that 29 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 19 cars have a cracked windshield?

Question ID: 0434400742

There are a total of 71 cars currently at a local garage. Of these, 58 cars have a cracked windshield. Suppose that 13 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 8 cars have a cracked windshield?

Question ID: 0958920929

There are a total of 54 phones currently at a local repair shop. Of these, 24 phones have a cracked display. Suppose that 2 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 0 phones have a cracked display?

Question ID: 0409381005

There are a total of 81 cameras currently at a local repair shop. Of these, 8 cameras have a broken lens. Suppose that 2 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 1 cameras have a broken lens?

Question ID: 0299908702

There are a total of 90 patients currently at a local clinic. Of these, 38 patients have flu-like symptoms. Suppose that 35 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 20 patients have flu-like symptoms?

Question ID: 0371754800

There are a total of 48 patients currently at a local clinic. Of these, 43 patients have flu-like symptoms. Suppose that 4 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 3 patients have flu-like symptoms?

Question ID: 0573172994

There are a total of 34 cameras currently at a local repair shop. Of these, 17 cameras have a broken lens. Suppose that 6 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 2 cameras have a broken lens?

Question ID: 0028044940

There are a total of 37 cars currently at a local garage. Of these, 2 cars have a cracked windshield. Suppose that 1 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 1 cars have a cracked windshield?

Question ID: 0479897490

There are a total of 30 cars currently at a local garage. Of these, 16 cars have a cracked windshield. Suppose that 13 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 6 cars have a cracked windshield?

Question ID: 0494475544

There are a total of 82 phones currently at a local repair shop. Of these, 5 phones have a cracked display. Suppose that 3 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 0 phones have a cracked display?

Question ID: 0605353780

There are a total of 36 patients currently at a local clinic. Of these, 34 patients have flu-like symptoms. Suppose that 1 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0300278251

There are a total of 58 patients currently at a local clinic. Of these, 43 patients have flu-like symptoms. Suppose that 4 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0278901753

There are a total of 50 cars currently at a local garage. Of these, 6 cars have a cracked windshield. Suppose that 2 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 2 cars have a cracked windshield?

Question ID: 0270604488

There are a total of 52 patients currently at a local clinic. Of these, 30 patients have flu-like symptoms. Suppose that 12 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 9 patients have flu-like symptoms?

Question ID: 0049465180

There are a total of 21 computers currently at a local repair shop. Of these, 17 computers have a broken screen. Suppose that 4 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 4 computers have a broken screen?

Question ID: 0932992696

There are a total of 43 phones currently at a local repair shop. Of these, 19 phones have a cracked display. Suppose that 5 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 1 phones have a cracked display?

Question ID: 0201413517

There are a total of 39 cars currently at a local garage. Of these, 31 cars have a cracked windshield. Suppose that 2 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 0 cars have a cracked windshield?

Question ID: 0760932615

There are a total of 82 patients currently at a local clinic. Of these, 18 patients have flu-like symptoms. Suppose that 6 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 1 patients have flu-like symptoms?

Question ID: 0965722847

There are a total of 39 computers currently at a local repair shop. Of these, 25 computers have a broken screen. Suppose that 2 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 1 computers have a broken screen?

Question ID: 0053633068

There are a total of 34 computers currently at a local repair shop. Of these, 22 computers have a broken screen. Suppose that 8 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 4 computers have a broken screen?

Question ID: 0139482500

There are a total of 39 computers currently at a local repair shop. Of these, 24 computers have a broken screen. Suppose that 14 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 10 computers have a broken screen?

Question ID: 0119262355

There are a total of 81 phones currently at a local repair shop. Of these, 46 phones have a cracked display. Suppose that 6 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 5 phones have a cracked display?

Question ID: 0696754503

There are a total of 91 cameras currently at a local repair shop. Of these, 80 cameras have a broken lens. Suppose that 10 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 10 cameras have a broken lens?

Question ID: 0214933103

There are a total of 60 computers currently at a local repair shop. Of these, 26 computers have a broken screen. Suppose that 19 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 9 computers have a broken screen?

Question ID: 0195429313

There are a total of 93 patients currently at a local clinic. Of these, 58 patients have flu-like symptoms. Suppose that 29 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 14 patients have flu-like symptoms?

Question ID: 0813296039

There are a total of 82 computers currently at a local repair shop. Of these, 66 computers have a broken screen. Suppose that 13 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 13 computers have a broken screen?

Question ID: 0944210164

There are a total of 68 computers currently at a local repair shop. Of these, 59 computers have a broken screen. Suppose that 7 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 4 computers have a broken screen?

Question ID: 0496402832

There are a total of 78 computers currently at a local repair shop. Of these, 22 computers have a broken screen. Suppose that 20 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 9 computers have a broken screen?

Question ID: 0956899268

There are a total of 39 computers currently at a local repair shop. Of these, 25 computers have a broken screen. Suppose that 8 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 5 computers have a broken screen?

Question ID: 0894428963

There are a total of 42 cars currently at a local garage. Of these, 21 cars have a cracked windshield. Suppose that 5 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 5 cars have a cracked windshield?

Question ID: 0891521978

There are a total of 39 phones currently at a local repair shop. Of these, 7 phones have a cracked display. Suppose that 4 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 0 phones have a cracked display?

Question ID: 0213395856

There are a total of 23 computers currently at a local repair shop. Of these, 12 computers have a broken screen. Suppose that 10 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 8 computers have a broken screen?

Question ID: 0688396268

There are a total of 50 phones currently at a local repair shop. Of these, 23 phones have a cracked display. Suppose that 7 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 1 phones have a cracked display?

Question ID: 0027258236

There are a total of 53 patients currently at a local clinic. Of these, 44 patients have flu-like symptoms. Suppose that 3 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 3 patients have flu-like symptoms?

Question ID: 0465283125

There are a total of 36 phones currently at a local repair shop. Of these, 8 phones have a cracked display. Suppose that 7 phones are selected at random.

How many phones should we expect to have a cracked display?
What is the probability that, of those selected, exactly 1 phones have a cracked display?

Question ID: 0272911223

There are a total of 48 computers currently at a local repair shop. Of these, 13 computers have a broken screen. Suppose that 2 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 1 computers have a broken screen?

Question ID: 0759833782

There are a total of 96 cameras currently at a local repair shop. Of these, 31 cameras have a broken lens. Suppose that 6 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 1 cameras have a broken lens?

Question ID: 0068491721

There are a total of 47 patients currently at a local clinic. Of these, 5 patients have flu-like symptoms. Suppose that 2 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 0 patients have flu-like symptoms?

Question ID: 0291971573

There are a total of 90 patients currently at a local clinic. Of these, 70 patients have flu-like symptoms. Suppose that 8 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 7 patients have flu-like symptoms?

Question ID: 0564247431

There are a total of 99 computers currently at a local repair shop. Of these, 18 computers have a broken screen. Suppose that 2 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 2 computers have a broken screen?

Question ID: 0778260048

There are a total of 71 cars currently at a local garage. Of these, 43 cars have a cracked windshield. Suppose that 18 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 12 cars have a cracked windshield?

Question ID: 0938584816

There are a total of 48 patients currently at a local clinic. Of these, 31 patients have flu-like symptoms. Suppose that 6 patients are selected at random.

How many patients should we expect to have flu-like symptoms?
What is the probability that, of those selected, exactly 6 patients have flu-like symptoms?

Question ID: 0832284513

There are a total of 60 computers currently at a local repair shop. Of these, 20 computers have a broken screen. Suppose that 13 computers are selected at random.

How many computers should we expect to have a broken screen?
What is the probability that, of those selected, exactly 3 computers have a broken screen?

Question ID: 0684702067

There are a total of 100 cameras currently at a local repair shop. Of these, 69 cameras have a broken lens. Suppose that 30 cameras are selected at random.

How many cameras should we expect to have a broken lens?
What is the probability that, of those selected, exactly 21 cameras have a broken lens?

Question ID: 0847912187

There are a total of 96 cars currently at a local garage. Of these, 9 cars have a cracked windshield. Suppose that 8 cars are selected at random.

How many cars should we expect to have a cracked windshield?
What is the probability that, of those selected, exactly 0 cars have a cracked windshield?

Question ID: 0500548759

Self Assessment 8.9

The probability of a complication for a patient at an ICU occuring during any hour is 0.2.

What is the probability that the first complication for the patient occurs during hour 12?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0756661837

The probability of a car accident at a particular intersection occuring during any specific month is 0.36.

What is the probability that the first car accident at the particular intersection occurs in month 5?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0331081826

The probability of a complication for a patient at an ICU occuring during any hour is 0.42.

What is the probability that the first complication for the patient occurs during hour 3?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0738594471

The probability of a car accident at a particular intersection occuring during any specific month is 0.18.

What is the probability that the first car accident at the particular intersection occurs in month 13?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0149213522

The probability of a car accident at a particular intersection occuring during any specific month is 0.27.

What is the probability that the first car accident at the particular intersection occurs in month 1?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0900182458

The probability of a computer crash occuring on any particular day is 0.22.

What is the probability that the first computer crash occurs on day 12?
What is the probability that, by day 4, the first computer crash has still not occured ?

Question ID: 0074193594

The probability of a complication for a patient at an ICU occuring during any hour is 0.49.

What is the probability that the first complication for the patient occurs during hour 4?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0697565219

The probability of a defective item being produced occuring the production of any item is 0.25.

What is the probability that the first defective item produced is item 8?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0428693396

The probability of a defective item being produced occuring the production of any item is 0.33.

What is the probability that the first defective item produced is item 6?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0102782512

The probability of a complication for a patient at an ICU occuring during any hour is 0.04.

What is the probability that the first complication for the patient occurs during hour 20?
What is the probability that, by hour 2, the first complication for the patient has still not occured ?

Question ID: 0636666062

The probability of a defective item being produced occuring the production of any item is 0.24.

What is the probability that the first defective item produced is item 3?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0567191172

The probability of a car accident at a particular intersection occuring during any specific month is 0.07.

What is the probability that the first car accident at the particular intersection occurs in month 2?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0708825001

The probability of a computer crash occuring on any particular day is 0.06.

What is the probability that the first computer crash occurs on day 29?
What is the probability that, by day 2, the first computer crash has still not occured ?

Question ID: 0027077296

The probability of a defective item being produced occuring the production of any item is 0.38.

What is the probability that the first defective item produced is item 6?
What is the probability that, by item 2, the first defective item produced has still not occured ?

Question ID: 0692487170

The probability of a car accident at a particular intersection occuring during any specific month is 0.2.

What is the probability that the first car accident at the particular intersection occurs in month 9?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0329378476

The probability of a defective item being produced occuring the production of any item is 0.18.

What is the probability that the first defective item produced is item 11?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0303906912

The probability of a computer crash occuring on any particular day is 0.27.

What is the probability that the first computer crash occurs on day 10?
What is the probability that, by day 4, the first computer crash has still not occured ?

Question ID: 0314147640

The probability of a computer crash occuring on any particular day is 0.19.

What is the probability that the first computer crash occurs on day 8?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0072848675

The probability of a complication for a patient at an ICU occuring during any hour is 0.37.

What is the probability that the first complication for the patient occurs during hour 6?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0361164053

The probability of a computer crash occuring on any particular day is 0.15.

What is the probability that the first computer crash occurs on day 1?
What is the probability that, by day 4, the first computer crash has still not occured ?

Question ID: 0130610263

The probability of a defective item being produced occuring the production of any item is 0.21.

What is the probability that the first defective item produced is item 6?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0824746045

The probability of a defective item being produced occuring the production of any item is 0.35.

What is the probability that the first defective item produced is item 9?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0323076977

The probability of a defective item being produced occuring the production of any item is 0.44.

What is the probability that the first defective item produced is item 3?
What is the probability that, by item 2, the first defective item produced has still not occured ?

Question ID: 0372273482

The probability of a car accident at a particular intersection occuring during any specific month is 0.13.

What is the probability that the first car accident at the particular intersection occurs in month 11?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0872692639

The probability of a car accident at a particular intersection occuring during any specific month is 0.33.

What is the probability that the first car accident at the particular intersection occurs in month 3?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0537812280

The probability of a computer crash occuring on any particular day is 0.47.

What is the probability that the first computer crash occurs on day 7?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0568078314

The probability of a car accident at a particular intersection occuring during any specific month is 0.34.

What is the probability that the first car accident at the particular intersection occurs in month 9?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0943560149

The probability of a defective item being produced occuring the production of any item is 0.34.

What is the probability that the first defective item produced is item 8?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0966578110

The probability of a defective item being produced occuring the production of any item is 0.15.

What is the probability that the first defective item produced is item 11?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0659410305

The probability of a computer crash occuring on any particular day is 0.02.

What is the probability that the first computer crash occurs on day 4?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0069665917

The probability of a car accident at a particular intersection occuring during any specific month is 0.23.

What is the probability that the first car accident at the particular intersection occurs in month 7?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0465486744

The probability of a complication for a patient at an ICU occuring during any hour is 0.13.

What is the probability that the first complication for the patient occurs during hour 4?
What is the probability that, by hour 5, the first complication for the patient has still not occured ?

Question ID: 0731956289

The probability of a computer crash occuring on any particular day is 0.45.

What is the probability that the first computer crash occurs on day 2?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0146049314

The probability of a defective item being produced occuring the production of any item is 0.07.

What is the probability that the first defective item produced is item 24?
What is the probability that, by item 4, the first defective item produced has still not occured ?

Question ID: 0321106014

The probability of a defective item being produced occuring the production of any item is 0.06.

What is the probability that the first defective item produced is item 13?
What is the probability that, by item 4, the first defective item produced has still not occured ?

Question ID: 0634281645

The probability of a car accident at a particular intersection occuring during any specific month is 0.36.

What is the probability that the first car accident at the particular intersection occurs in month 2?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0509077287

The probability of a car accident at a particular intersection occuring during any specific month is 0.36.

What is the probability that the first car accident at the particular intersection occurs in month 2?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0208905782

The probability of a computer crash occuring on any particular day is 0.02.

What is the probability that the first computer crash occurs on day 31?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0225436093

The probability of a computer crash occuring on any particular day is 0.46.

What is the probability that the first computer crash occurs on day 6?
What is the probability that, by day 4, the first computer crash has still not occured ?

Question ID: 0909927970

The probability of a complication for a patient at an ICU occuring during any hour is 0.11.

What is the probability that the first complication for the patient occurs during hour 3?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0803188200

The probability of a car accident at a particular intersection occuring during any specific month is 0.41.

What is the probability that the first car accident at the particular intersection occurs in month 2?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0171460080

The probability of a complication for a patient at an ICU occuring during any hour is 0.12.

What is the probability that the first complication for the patient occurs during hour 4?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0354693163

The probability of a car accident at a particular intersection occuring during any specific month is 0.44.

What is the probability that the first car accident at the particular intersection occurs in month 3?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0533963420

The probability of a computer crash occuring on any particular day is 0.09.

What is the probability that the first computer crash occurs on day 17?
What is the probability that, by day 2, the first computer crash has still not occured ?

Question ID: 0260779464

The probability of a car accident at a particular intersection occuring during any specific month is 0.03.

What is the probability that the first car accident at the particular intersection occurs in month 33?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0047785779

The probability of a car accident at a particular intersection occuring during any specific month is 0.42.

What is the probability that the first car accident at the particular intersection occurs in month 7?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0179408438

The probability of a complication for a patient at an ICU occuring during any hour is 0.32.

What is the probability that the first complication for the patient occurs during hour 4?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0406610741

The probability of a complication for a patient at an ICU occuring during any hour is 0.38.

What is the probability that the first complication for the patient occurs during hour 2?
What is the probability that, by hour 2, the first complication for the patient has still not occured ?

Question ID: 0497369178

The probability of a computer crash occuring on any particular day is 0.25.

What is the probability that the first computer crash occurs on day 7?
What is the probability that, by day 2, the first computer crash has still not occured ?

Question ID: 0837593448

The probability of a complication for a patient at an ICU occuring during any hour is 0.03.

What is the probability that the first complication for the patient occurs during hour 35?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0374259708

The probability of a complication for a patient at an ICU occuring during any hour is 0.4.

What is the probability that the first complication for the patient occurs during hour 8?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0138913450

The probability of a car accident at a particular intersection occuring during any specific month is 0.04.

What is the probability that the first car accident at the particular intersection occurs in month 1?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0800202583

The probability of a car accident at a particular intersection occuring during any specific month is 0.03.

What is the probability that the first car accident at the particular intersection occurs in month 25?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0196825873

The probability of a complication for a patient at an ICU occuring during any hour is 0.39.

What is the probability that the first complication for the patient occurs during hour 7?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0045838577

The probability of a computer crash occuring on any particular day is 0.06.

What is the probability that the first computer crash occurs on day 24?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0927627693

The probability of a complication for a patient at an ICU occuring during any hour is 0.26.

What is the probability that the first complication for the patient occurs during hour 7?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0828644520

The probability of a car accident at a particular intersection occuring during any specific month is 0.41.

What is the probability that the first car accident at the particular intersection occurs in month 3?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0191452007

The probability of a car accident at a particular intersection occuring during any specific month is 0.09.

What is the probability that the first car accident at the particular intersection occurs in month 1?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0690387214

The probability of a computer crash occuring on any particular day is 0.02.

What is the probability that the first computer crash occurs on day 33?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0548322985

The probability of a complication for a patient at an ICU occuring during any hour is 0.47.

What is the probability that the first complication for the patient occurs during hour 3?
What is the probability that, by hour 2, the first complication for the patient has still not occured ?

Question ID: 0665103650

The probability of a complication for a patient at an ICU occuring during any hour is 0.34.

What is the probability that the first complication for the patient occurs during hour 2?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0624320098

The probability of a car accident at a particular intersection occuring during any specific month is 0.32.

What is the probability that the first car accident at the particular intersection occurs in month 1?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0399334012

The probability of a complication for a patient at an ICU occuring during any hour is 0.34.

What is the probability that the first complication for the patient occurs during hour 5?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0001088136

The probability of a car accident at a particular intersection occuring during any specific month is 0.13.

What is the probability that the first car accident at the particular intersection occurs in month 3?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0855198507

The probability of a defective item being produced occuring the production of any item is 0.34.

What is the probability that the first defective item produced is item 2?
What is the probability that, by item 2, the first defective item produced has still not occured ?

Question ID: 0648546193

The probability of a defective item being produced occuring the production of any item is 0.37.

What is the probability that the first defective item produced is item 6?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0886106133

The probability of a computer crash occuring on any particular day is 0.05.

What is the probability that the first computer crash occurs on day 28?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0581502177

The probability of a car accident at a particular intersection occuring during any specific month is 0.26.

What is the probability that the first car accident at the particular intersection occurs in month 1?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0537008925

The probability of a car accident at a particular intersection occuring during any specific month is 0.37.

What is the probability that the first car accident at the particular intersection occurs in month 3?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0827599961

The probability of a computer crash occuring on any particular day is 0.19.

What is the probability that the first computer crash occurs on day 7?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0708279034

The probability of a complication for a patient at an ICU occuring during any hour is 0.33.

What is the probability that the first complication for the patient occurs during hour 3?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0450649048

The probability of a defective item being produced occuring the production of any item is 0.33.

What is the probability that the first defective item produced is item 3?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0143254083

The probability of a defective item being produced occuring the production of any item is 0.15.

What is the probability that the first defective item produced is item 4?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0224599782

The probability of a computer crash occuring on any particular day is 0.37.

What is the probability that the first computer crash occurs on day 6?
What is the probability that, by day 2, the first computer crash has still not occured ?

Question ID: 0787899178

The probability of a car accident at a particular intersection occuring during any specific month is 0.09.

What is the probability that the first car accident at the particular intersection occurs in month 16?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0302732547

The probability of a car accident at a particular intersection occuring during any specific month is 0.18.

What is the probability that the first car accident at the particular intersection occurs in month 14?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0182927685

The probability of a computer crash occuring on any particular day is 0.42.

What is the probability that the first computer crash occurs on day 1?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0274492923

The probability of a defective item being produced occuring the production of any item is 0.27.

What is the probability that the first defective item produced is item 4?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0547398277

The probability of a car accident at a particular intersection occuring during any specific month is 0.12.

What is the probability that the first car accident at the particular intersection occurs in month 6?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0317727036

The probability of a complication for a patient at an ICU occuring during any hour is 0.33.

What is the probability that the first complication for the patient occurs during hour 8?
What is the probability that, by hour 5, the first complication for the patient has still not occured ?

Question ID: 0146996896

The probability of a car accident at a particular intersection occuring during any specific month is 0.31.

What is the probability that the first car accident at the particular intersection occurs in month 5?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0903889568

The probability of a defective item being produced occuring the production of any item is 0.15.

What is the probability that the first defective item produced is item 16?
What is the probability that, by item 4, the first defective item produced has still not occured ?

Question ID: 0310177704

The probability of a car accident at a particular intersection occuring during any specific month is 0.06.

What is the probability that the first car accident at the particular intersection occurs in month 7?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0238490399

The probability of a computer crash occuring on any particular day is 0.49.

What is the probability that the first computer crash occurs on day 6?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0528788982

The probability of a complication for a patient at an ICU occuring during any hour is 0.3.

What is the probability that the first complication for the patient occurs during hour 2?
What is the probability that, by hour 5, the first complication for the patient has still not occured ?

Question ID: 0618243021

The probability of a car accident at a particular intersection occuring during any specific month is 0.02.

What is the probability that the first car accident at the particular intersection occurs in month 16?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0537851626

The probability of a complication for a patient at an ICU occuring during any hour is 0.39.

What is the probability that the first complication for the patient occurs during hour 5?
What is the probability that, by hour 3, the first complication for the patient has still not occured ?

Question ID: 0351993594

The probability of a computer crash occuring on any particular day is 0.5.

What is the probability that the first computer crash occurs on day 5?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0910768395

The probability of a defective item being produced occuring the production of any item is 0.18.

What is the probability that the first defective item produced is item 7?
What is the probability that, by item 3, the first defective item produced has still not occured ?

Question ID: 0276747050

The probability of a defective item being produced occuring the production of any item is 0.37.

What is the probability that the first defective item produced is item 8?
What is the probability that, by item 2, the first defective item produced has still not occured ?

Question ID: 0515673653

The probability of a defective item being produced occuring the production of any item is 0.03.

What is the probability that the first defective item produced is item 12?
What is the probability that, by item 4, the first defective item produced has still not occured ?

Question ID: 0777598765

The probability of a car accident at a particular intersection occuring during any specific month is 0.2.

What is the probability that the first car accident at the particular intersection occurs in month 4?
What is the probability that, by month 3, the first car accident at the particular intersection has still not occured ?

Question ID: 0248646523

The probability of a defective item being produced occuring the production of any item is 0.07.

What is the probability that the first defective item produced is item 10?
What is the probability that, by item 5, the first defective item produced has still not occured ?

Question ID: 0626551268

The probability of a computer crash occuring on any particular day is 0.03.

What is the probability that the first computer crash occurs on day 12?
What is the probability that, by day 5, the first computer crash has still not occured ?

Question ID: 0671026361

The probability of a car accident at a particular intersection occuring during any specific month is 0.09.

What is the probability that the first car accident at the particular intersection occurs in month 11?
What is the probability that, by month 2, the first car accident at the particular intersection has still not occured ?

Question ID: 0563020156

The probability of a car accident at a particular intersection occuring during any specific month is 0.47.

What is the probability that the first car accident at the particular intersection occurs in month 7?
What is the probability that, by month 4, the first car accident at the particular intersection has still not occured ?

Question ID: 0796744368

The probability of a computer crash occuring on any particular day is 0.45.

What is the probability that the first computer crash occurs on day 3?
What is the probability that, by day 3, the first computer crash has still not occured ?

Question ID: 0486107367

The probability of a car accident at a particular intersection occuring during any specific month is 0.12.

What is the probability that the first car accident at the particular intersection occurs in month 11?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0388885159

The probability of a complication for a patient at an ICU occuring during any hour is 0.29.

What is the probability that the first complication for the patient occurs during hour 10?
What is the probability that, by hour 4, the first complication for the patient has still not occured ?

Question ID: 0559114327

The probability of a car accident at a particular intersection occuring during any specific month is 0.05.

What is the probability that the first car accident at the particular intersection occurs in month 15?
What is the probability that, by month 5, the first car accident at the particular intersection has still not occured ?

Question ID: 0512143086

Self Assessment 8.10

The probability of a car accident at a particular intersection occuring during any specific month is 0.38.

What is the probability that the 2nd car accident at the particular intersection occurs in month 9?
What is the probability that, by month 7, the 2nd car accident at the particular intersection has still not occured ?

Question ID: 0399139975

The probability of a car accident at a particular intersection occuring during any specific month is 0.46.

What is the probability that the 5th car accident at the particular intersection occurs in month 19?
What is the probability that, by month 5, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0643373853

The probability of a complication for a patient at an ICU occuring during any hour is 0.08.

What is the probability that the 10th complication for the patient occurs during hour 99?
What is the probability that, by hour 14, the 10th complication for the patient has still not occured ?

Question ID: 0125898888

The probability of a complication for a patient at an ICU occuring during any hour is 0.47.

What is the probability that the 7th complication for the patient occurs during hour 21?
What is the probability that, by hour 12, the 7th complication for the patient has still not occured ?

Question ID: 0933638428

The probability of a defective item being produced occuring the production of any item is 0.22.

What is the probability that the 2nd defective item produced is item 7?
What is the probability that, by item 2, the 2nd defective item produced has still not occured ?

Question ID: 0947513587

The probability of a complication for a patient at an ICU occuring during any hour is 0.31.

What is the probability that the 9th complication for the patient occurs during hour 40?
What is the probability that, by hour 12, the 9th complication for the patient has still not occured ?

Question ID: 0939350646

The probability of a computer crash occuring on any particular day is 0.35.

What is the probability that the 4th computer crash occurs on day 20?
What is the probability that, by day 8, the 4th computer crash has still not occured ?

Question ID: 0747403907

The probability of a car accident at a particular intersection occuring during any specific month is 0.27.

What is the probability that the 9th car accident at the particular intersection occurs in month 29?
What is the probability that, by month 12, the 9th car accident at the particular intersection has still not occured ?

Question ID: 0482297558

The probability of a complication for a patient at an ICU occuring during any hour is 0.17.

What is the probability that the 6th complication for the patient occurs during hour 52?
What is the probability that, by hour 10, the 6th complication for the patient has still not occured ?

Question ID: 0614118033

The probability of a computer crash occuring on any particular day is 0.09.

What is the probability that the 4th computer crash occurs on day 60?
What is the probability that, by day 5, the 4th computer crash has still not occured ?

Question ID: 0566600854

The probability of a car accident at a particular intersection occuring during any specific month is 0.21.

What is the probability that the 5th car accident at the particular intersection occurs in month 32?
What is the probability that, by month 5, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0139275608

The probability of a complication for a patient at an ICU occuring during any hour is 0.1.

What is the probability that the 8th complication for the patient occurs during hour 88?
What is the probability that, by hour 8, the 8th complication for the patient has still not occured ?

Question ID: 0109713514

The probability of a computer crash occuring on any particular day is 0.4.

What is the probability that the 6th computer crash occurs on day 21?
What is the probability that, by day 7, the 6th computer crash has still not occured ?

Question ID: 0154662894

The probability of a complication for a patient at an ICU occuring during any hour is 0.09.

What is the probability that the 10th complication for the patient occurs during hour 86?
What is the probability that, by hour 10, the 10th complication for the patient has still not occured ?

Question ID: 0464947735

The probability of a complication for a patient at an ICU occuring during any hour is 0.07.

What is the probability that the 7th complication for the patient occurs during hour 94?
What is the probability that, by hour 11, the 7th complication for the patient has still not occured ?

Question ID: 0828327895

The probability of a car accident at a particular intersection occuring during any specific month is 0.37.

What is the probability that the 8th car accident at the particular intersection occurs in month 32?
What is the probability that, by month 13, the 8th car accident at the particular intersection has still not occured ?

Question ID: 0219131150

The probability of a defective item being produced occuring the production of any item is 0.12.

What is the probability that the 9th defective item produced is item 48?
What is the probability that, by item 9, the 9th defective item produced has still not occured ?

Question ID: 0673851373

The probability of a defective item being produced occuring the production of any item is 0.48.

What is the probability that the 9th defective item produced is item 21?
What is the probability that, by item 11, the 9th defective item produced has still not occured ?

Question ID: 0864561888

The probability of a car accident at a particular intersection occuring during any specific month is 0.03.

What is the probability that the 8th car accident at the particular intersection occurs in month 17?
What is the probability that, by month 12, the 8th car accident at the particular intersection has still not occured ?

Question ID: 0890191992

The probability of a defective item being produced occuring the production of any item is 0.41.

What is the probability that the 2nd defective item produced is item 6?
What is the probability that, by item 2, the 2nd defective item produced has still not occured ?

Question ID: 0378216084

The probability of a defective item being produced occuring the production of any item is 0.25.

What is the probability that the 6th defective item produced is item 15?
What is the probability that, by item 9, the 6th defective item produced has still not occured ?

Question ID: 0585274402

The probability of a defective item being produced occuring the production of any item is 0.36.

What is the probability that the 9th defective item produced is item 19?
What is the probability that, by item 12, the 9th defective item produced has still not occured ?

Question ID: 0560067708

The probability of a car accident at a particular intersection occuring during any specific month is 0.38.

What is the probability that the 7th car accident at the particular intersection occurs in month 17?
What is the probability that, by month 7, the 7th car accident at the particular intersection has still not occured ?

Question ID: 0084006745

The probability of a computer crash occuring on any particular day is 0.27.

What is the probability that the 2nd computer crash occurs on day 14?
What is the probability that, by day 7, the 2nd computer crash has still not occured ?

Question ID: 0586310385

The probability of a defective item being produced occuring the production of any item is 0.48.

What is the probability that the 10th defective item produced is item 30?
What is the probability that, by item 10, the 10th defective item produced has still not occured ?

Question ID: 0061218189

The probability of a computer crash occuring on any particular day is 0.43.

What is the probability that the 8th computer crash occurs on day 20?
What is the probability that, by day 12, the 8th computer crash has still not occured ?

Question ID: 0709672968

The probability of a complication for a patient at an ICU occuring during any hour is 0.49.

What is the probability that the 9th complication for the patient occurs during hour 14?
What is the probability that, by hour 10, the 9th complication for the patient has still not occured ?

Question ID: 0528538692

The probability of a car accident at a particular intersection occuring during any specific month is 0.04.

What is the probability that the 2nd car accident at the particular intersection occurs in month 27?
What is the probability that, by month 3, the 2nd car accident at the particular intersection has still not occured ?

Question ID: 0771201284

The probability of a complication for a patient at an ICU occuring during any hour is 0.25.

What is the probability that the 6th complication for the patient occurs during hour 31?
What is the probability that, by hour 11, the 6th complication for the patient has still not occured ?

Question ID: 0496708830

The probability of a defective item being produced occuring the production of any item is 0.18.

What is the probability that the 6th defective item produced is item 23?
What is the probability that, by item 6, the 6th defective item produced has still not occured ?

Question ID: 0768671926

The probability of a complication for a patient at an ICU occuring during any hour is 0.31.

What is the probability that the 10th complication for the patient occurs during hour 23?
What is the probability that, by hour 12, the 10th complication for the patient has still not occured ?

Question ID: 0349924246

The probability of a computer crash occuring on any particular day is 0.15.

What is the probability that the 8th computer crash occurs on day 50?
What is the probability that, by day 9, the 8th computer crash has still not occured ?

Question ID: 0686900775

The probability of a defective item being produced occuring the production of any item is 0.42.

What is the probability that the 7th defective item produced is item 24?
What is the probability that, by item 12, the 7th defective item produced has still not occured ?

Question ID: 0336415538

The probability of a car accident at a particular intersection occuring during any specific month is 0.38.

What is the probability that the 3rd car accident at the particular intersection occurs in month 3?
What is the probability that, by month 6, the 3rd car accident at the particular intersection has still not occured ?

Question ID: 0412633206

The probability of a complication for a patient at an ICU occuring during any hour is 0.31.

What is the probability that the 8th complication for the patient occurs during hour 16?
What is the probability that, by hour 11, the 8th complication for the patient has still not occured ?

Question ID: 0502645215

The probability of a complication for a patient at an ICU occuring during any hour is 0.33.

What is the probability that the 4th complication for the patient occurs during hour 9?
What is the probability that, by hour 8, the 4th complication for the patient has still not occured ?

Question ID: 0599073281

The probability of a complication for a patient at an ICU occuring during any hour is 0.06.

What is the probability that the 9th complication for the patient occurs during hour 67?
What is the probability that, by hour 12, the 9th complication for the patient has still not occured ?

Question ID: 0863636978

The probability of a computer crash occuring on any particular day is 0.25.

What is the probability that the 5th computer crash occurs on day 25?
What is the probability that, by day 5, the 5th computer crash has still not occured ?

Question ID: 0901935883

The probability of a complication for a patient at an ICU occuring during any hour is 0.38.

What is the probability that the 7th complication for the patient occurs during hour 18?
What is the probability that, by hour 11, the 7th complication for the patient has still not occured ?

Question ID: 0372010215

The probability of a complication for a patient at an ICU occuring during any hour is 0.26.

What is the probability that the 7th complication for the patient occurs during hour 26?
What is the probability that, by hour 9, the 7th complication for the patient has still not occured ?

Question ID: 0938447728

The probability of a computer crash occuring on any particular day is 0.11.

What is the probability that the 6th computer crash occurs on day 37?
What is the probability that, by day 11, the 6th computer crash has still not occured ?

Question ID: 0128243187

The probability of a car accident at a particular intersection occuring during any specific month is 0.4.

What is the probability that the 10th car accident at the particular intersection occurs in month 27?
What is the probability that, by month 15, the 10th car accident at the particular intersection has still not occured ?

Question ID: 0309886113

The probability of a complication for a patient at an ICU occuring during any hour is 0.11.

What is the probability that the 3rd complication for the patient occurs during hour 12?
What is the probability that, by hour 5, the 3rd complication for the patient has still not occured ?

Question ID: 0461237994

The probability of a car accident at a particular intersection occuring during any specific month is 0.06.

What is the probability that the 5th car accident at the particular intersection occurs in month 55?
What is the probability that, by month 9, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0807944433

The probability of a complication for a patient at an ICU occuring during any hour is 0.45.

What is the probability that the 2nd complication for the patient occurs during hour 8?
What is the probability that, by hour 4, the 2nd complication for the patient has still not occured ?

Question ID: 0672165937

The probability of a computer crash occuring on any particular day is 0.47.

What is the probability that the 6th computer crash occurs on day 21?
What is the probability that, by day 10, the 6th computer crash has still not occured ?

Question ID: 0908118433

The probability of a complication for a patient at an ICU occuring during any hour is 0.26.

What is the probability that the 9th complication for the patient occurs during hour 27?
What is the probability that, by hour 10, the 9th complication for the patient has still not occured ?

Question ID: 0769795614

The probability of a computer crash occuring on any particular day is 0.5.

What is the probability that the 5th computer crash occurs on day 10?
What is the probability that, by day 9, the 5th computer crash has still not occured ?

Question ID: 0117415745

The probability of a computer crash occuring on any particular day is 0.22.

What is the probability that the 7th computer crash occurs on day 47?
What is the probability that, by day 12, the 7th computer crash has still not occured ?

Question ID: 0121074044

The probability of a computer crash occuring on any particular day is 0.13.

What is the probability that the 2nd computer crash occurs on day 20?
What is the probability that, by day 3, the 2nd computer crash has still not occured ?

Question ID: 0785799397

The probability of a car accident at a particular intersection occuring during any specific month is 0.16.

What is the probability that the 8th car accident at the particular intersection occurs in month 52?
What is the probability that, by month 12, the 8th car accident at the particular intersection has still not occured ?

Question ID: 0136946413

The probability of a car accident at a particular intersection occuring during any specific month is 0.19.

What is the probability that the 5th car accident at the particular intersection occurs in month 13?
What is the probability that, by month 5, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0614757654

The probability of a computer crash occuring on any particular day is 0.13.

What is the probability that the 6th computer crash occurs on day 37?
What is the probability that, by day 9, the 6th computer crash has still not occured ?

Question ID: 0155296573

The probability of a computer crash occuring on any particular day is 0.39.

What is the probability that the 8th computer crash occurs on day 12?
What is the probability that, by day 8, the 8th computer crash has still not occured ?

Question ID: 0613325272

The probability of a computer crash occuring on any particular day is 0.43.

What is the probability that the 10th computer crash occurs on day 25?
What is the probability that, by day 11, the 10th computer crash has still not occured ?

Question ID: 0853105662

The probability of a computer crash occuring on any particular day is 0.29.

What is the probability that the 7th computer crash occurs on day 27?
What is the probability that, by day 10, the 7th computer crash has still not occured ?

Question ID: 0604090413

The probability of a defective item being produced occuring the production of any item is 0.02.

What is the probability that the 2nd defective item produced is item 22?
What is the probability that, by item 4, the 2nd defective item produced has still not occured ?

Question ID: 0007885965

The probability of a computer crash occuring on any particular day is 0.2.

What is the probability that the 3rd computer crash occurs on day 25?
What is the probability that, by day 3, the 3rd computer crash has still not occured ?

Question ID: 0924622641

The probability of a computer crash occuring on any particular day is 0.2.

What is the probability that the 10th computer crash occurs on day 63?
What is the probability that, by day 15, the 10th computer crash has still not occured ?

Question ID: 0306027698

The probability of a car accident at a particular intersection occuring during any specific month is 0.03.

What is the probability that the 4th car accident at the particular intersection occurs in month 61?
What is the probability that, by month 4, the 4th car accident at the particular intersection has still not occured ?

Question ID: 0227817651

The probability of a complication for a patient at an ICU occuring during any hour is 0.32.

What is the probability that the 5th complication for the patient occurs during hour 20?
What is the probability that, by hour 8, the 5th complication for the patient has still not occured ?

Question ID: 0287608022

The probability of a computer crash occuring on any particular day is 0.38.

What is the probability that the 3rd computer crash occurs on day 5?
What is the probability that, by day 5, the 3rd computer crash has still not occured ?

Question ID: 0279373807

The probability of a defective item being produced occuring the production of any item is 0.15.

What is the probability that the 8th defective item produced is item 42?
What is the probability that, by item 9, the 8th defective item produced has still not occured ?

Question ID: 0332222333

The probability of a complication for a patient at an ICU occuring during any hour is 0.39.

What is the probability that the 10th complication for the patient occurs during hour 24?
What is the probability that, by hour 12, the 10th complication for the patient has still not occured ?

Question ID: 0545551537

The probability of a computer crash occuring on any particular day is 0.18.

What is the probability that the 4th computer crash occurs on day 12?
What is the probability that, by day 6, the 4th computer crash has still not occured ?

Question ID: 0511799518

The probability of a defective item being produced occuring the production of any item is 0.28.

What is the probability that the 10th defective item produced is item 41?
What is the probability that, by item 15, the 10th defective item produced has still not occured ?

Question ID: 0762625384

The probability of a defective item being produced occuring the production of any item is 0.21.

What is the probability that the 3rd defective item produced is item 14?
What is the probability that, by item 7, the 3rd defective item produced has still not occured ?

Question ID: 0196876371

The probability of a car accident at a particular intersection occuring during any specific month is 0.39.

What is the probability that the 5th car accident at the particular intersection occurs in month 19?
What is the probability that, by month 5, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0229981120

The probability of a complication for a patient at an ICU occuring during any hour is 0.34.

What is the probability that the 9th complication for the patient occurs during hour 16?
What is the probability that, by hour 14, the 9th complication for the patient has still not occured ?

Question ID: 0952007568

The probability of a computer crash occuring on any particular day is 0.28.

What is the probability that the 8th computer crash occurs on day 35?
What is the probability that, by day 11, the 8th computer crash has still not occured ?

Question ID: 0102683963

The probability of a computer crash occuring on any particular day is 0.45.

What is the probability that the 4th computer crash occurs on day 14?
What is the probability that, by day 8, the 4th computer crash has still not occured ?

Question ID: 0349424687

The probability of a defective item being produced occuring the production of any item is 0.26.

What is the probability that the 8th defective item produced is item 41?
What is the probability that, by item 8, the 8th defective item produced has still not occured ?

Question ID: 0913174291

The probability of a complication for a patient at an ICU occuring during any hour is 0.27.

What is the probability that the 8th complication for the patient occurs during hour 17?
What is the probability that, by hour 13, the 8th complication for the patient has still not occured ?

Question ID: 0908309391

The probability of a defective item being produced occuring the production of any item is 0.18.

What is the probability that the 4th defective item produced is item 23?
What is the probability that, by item 9, the 4th defective item produced has still not occured ?

Question ID: 0372726330

The probability of a defective item being produced occuring the production of any item is 0.41.

What is the probability that the 6th defective item produced is item 14?
What is the probability that, by item 11, the 6th defective item produced has still not occured ?

Question ID: 0060510572

The probability of a computer crash occuring on any particular day is 0.39.

What is the probability that the 3rd computer crash occurs on day 7?
What is the probability that, by day 4, the 3rd computer crash has still not occured ?

Question ID: 0070009089

The probability of a complication for a patient at an ICU occuring during any hour is 0.43.

What is the probability that the 8th complication for the patient occurs during hour 26?
What is the probability that, by hour 10, the 8th complication for the patient has still not occured ?

Question ID: 0979725732

The probability of a complication for a patient at an ICU occuring during any hour is 0.17.

What is the probability that the 6th complication for the patient occurs during hour 26?
What is the probability that, by hour 7, the 6th complication for the patient has still not occured ?

Question ID: 0640559725

The probability of a car accident at a particular intersection occuring during any specific month is 0.07.

What is the probability that the 6th car accident at the particular intersection occurs in month 65?
What is the probability that, by month 9, the 6th car accident at the particular intersection has still not occured ?

Question ID: 0186550658

The probability of a defective item being produced occuring the production of any item is 0.01.

What is the probability that the 7th defective item produced is item 32?
What is the probability that, by item 7, the 7th defective item produced has still not occured ?

Question ID: 0289369915

The probability of a computer crash occuring on any particular day is 0.14.

What is the probability that the 7th computer crash occurs on day 66?
What is the probability that, by day 8, the 7th computer crash has still not occured ?

Question ID: 0935257748

The probability of a defective item being produced occuring the production of any item is 0.31.

What is the probability that the 7th defective item produced is item 35?
What is the probability that, by item 11, the 7th defective item produced has still not occured ?

Question ID: 0019546255

The probability of a defective item being produced occuring the production of any item is 0.28.

What is the probability that the 10th defective item produced is item 40?
What is the probability that, by item 13, the 10th defective item produced has still not occured ?

Question ID: 0013469289

The probability of a complication for a patient at an ICU occuring during any hour is 0.13.

What is the probability that the 8th complication for the patient occurs during hour 77?
What is the probability that, by hour 8, the 8th complication for the patient has still not occured ?

Question ID: 0220366457

The probability of a computer crash occuring on any particular day is 0.41.

What is the probability that the 10th computer crash occurs on day 27?
What is the probability that, by day 13, the 10th computer crash has still not occured ?

Question ID: 0364030556

The probability of a defective item being produced occuring the production of any item is 0.08.

What is the probability that the 10th defective item produced is item 99?
What is the probability that, by item 11, the 10th defective item produced has still not occured ?

Question ID: 0649811559

The probability of a computer crash occuring on any particular day is 0.15.

What is the probability that the 4th computer crash occurs on day 12?
What is the probability that, by day 9, the 4th computer crash has still not occured ?

Question ID: 0672827205

The probability of a complication for a patient at an ICU occuring during any hour is 0.24.

What is the probability that the 9th complication for the patient occurs during hour 52?
What is the probability that, by hour 12, the 9th complication for the patient has still not occured ?

Question ID: 0439880023

The probability of a complication for a patient at an ICU occuring during any hour is 0.25.

What is the probability that the 8th complication for the patient occurs during hour 41?
What is the probability that, by hour 9, the 8th complication for the patient has still not occured ?

Question ID: 0587489132

The probability of a computer crash occuring on any particular day is 0.04.

What is the probability that the 7th computer crash occurs on day 17?
What is the probability that, by day 7, the 7th computer crash has still not occured ?

Question ID: 0405885521

The probability of a defective item being produced occuring the production of any item is 0.04.

What is the probability that the 5th defective item produced is item 44?
What is the probability that, by item 8, the 5th defective item produced has still not occured ?

Question ID: 0413447440

The probability of a computer crash occuring on any particular day is 0.37.

What is the probability that the 10th computer crash occurs on day 32?
What is the probability that, by day 12, the 10th computer crash has still not occured ?

Question ID: 0626459428

The probability of a car accident at a particular intersection occuring during any specific month is 0.38.

What is the probability that the 5th car accident at the particular intersection occurs in month 20?
What is the probability that, by month 10, the 5th car accident at the particular intersection has still not occured ?

Question ID: 0874749745

The probability of a car accident at a particular intersection occuring during any specific month is 0.06.

What is the probability that the 2nd car accident at the particular intersection occurs in month 22?
What is the probability that, by month 6, the 2nd car accident at the particular intersection has still not occured ?

Question ID: 0429208134

The probability of a car accident at a particular intersection occuring during any specific month is 0.17.

What is the probability that the 7th car accident at the particular intersection occurs in month 57?
What is the probability that, by month 8, the 7th car accident at the particular intersection has still not occured ?

Question ID: 0867005616

The probability of a computer crash occuring on any particular day is 0.23.

What is the probability that the 10th computer crash occurs on day 25?
What is the probability that, by day 12, the 10th computer crash has still not occured ?

Question ID: 0116526310

The probability of a complication for a patient at an ICU occuring during any hour is 0.5.

What is the probability that the 6th complication for the patient occurs during hour 8?
What is the probability that, by hour 8, the 6th complication for the patient has still not occured ?

Question ID: 0377381017

The probability of a defective item being produced occuring the production of any item is 0.28.

What is the probability that the 9th defective item produced is item 31?
What is the probability that, by item 12, the 9th defective item produced has still not occured ?

Question ID: 0562356753

The probability of a defective item being produced occuring the production of any item is 0.25.

What is the probability that the 2nd defective item produced is item 5?
What is the probability that, by item 3, the 2nd defective item produced has still not occured ?

Question ID: 0750198355

The probability of a complication for a patient at an ICU occuring during any hour is 0.29.

What is the probability that the 10th complication for the patient occurs during hour 37?
What is the probability that, by hour 10, the 10th complication for the patient has still not occured ?

Question ID: 0582349345

Self Assessment 8.11

Suppose that computer crashes occur at a rate of 6.7 per day.

What is the probability that 5 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0116531450

Suppose that complications for a patient at an ICU occur at a rate of 3.24 per stay.

What is the probability that 8 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0850090531

Suppose that computer crashes occur at a rate of 5.17 per day.

What is the probability that 9 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0740559247

Suppose that arrivals to an emergency room occur at a rate of 2.12 per quarter hour.

What is the probability that 4 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0348174798

Suppose that complications for a patient at an ICU occur at a rate of 9.06 per stay.

What is the probability that 12 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0389541002

Suppose that arrivals to an emergency room occur at a rate of 8.98 per quarter hour.

What is the probability that 6 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0937864858

Suppose that car accidents at a particular intersection occur at a rate of 3.95 per month.

What is the probability that 3 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0933542157

Suppose that car accidents at a particular intersection occur at a rate of 9.77 per month.

What is the probability that 9 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0528229967

Suppose that phone calls to a call center occur at a rate of 8.52 per minute.

What is the probability that 9 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0955748029

Suppose that arrivals to a store occur at a rate of 5.16 per hour.

What is the probability that 3 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0470485735

Suppose that complications for a patient at an ICU occur at a rate of 8.88 per stay.

What is the probability that 8 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0428825220

Suppose that complications for a patient at an ICU occur at a rate of 1.52 per stay.

What is the probability that 2 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0203277936

Suppose that arrivals to an emergency room occur at a rate of 6.72 per quarter hour.

What is the probability that 12 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0541224273

Suppose that complications for a patient at an ICU occur at a rate of 2.01 per stay.

What is the probability that 2 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0425359218

Suppose that phone calls to a call center occur at a rate of 3.84 per minute.

What is the probability that 5 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0422031743

Suppose that arrivals to an emergency room occur at a rate of 5.98 per quarter hour.

What is the probability that 11 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0237940923

Suppose that arrivals to a store occur at a rate of 5.36 per hour.

What is the probability that 5 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0309685920

Suppose that complications for a patient at an ICU occur at a rate of 6.29 per stay.

What is the probability that 8 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0405827707

Suppose that emails to a server occur at a rate of 8.6 per second.

What is the probability that 14 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0172085687

Suppose that complications for a patient at an ICU occur at a rate of 6.72 per stay.

What is the probability that 4 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0289567744

Suppose that computer crashes occur at a rate of 4.13 per day.

What is the probability that 2 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0934489917

Suppose that emails to a server occur at a rate of 7.28 per second.

What is the probability that 10 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0064993503

Suppose that complications for a patient at an ICU occur at a rate of 6.6 per stay.

What is the probability that 6 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0547722072

Suppose that arrivals to a store occur at a rate of 5.27 per hour.

What is the probability that 9 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0682591434

Suppose that emails to a server occur at a rate of 3.41 per second.

What is the probability that 8 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0997272987

Suppose that phone calls to a call center occur at a rate of 6.04 per minute.

What is the probability that 10 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0159899223

Suppose that car accidents at a particular intersection occur at a rate of 0.86 per month.

What is the probability that 2 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0249696945

Suppose that arrivals to a store occur at a rate of 9.27 per hour.

What is the probability that 4 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0571054508

Suppose that car accidents at a particular intersection occur at a rate of 9.12 per month.

What is the probability that 8 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0942488540

Suppose that complications for a patient at an ICU occur at a rate of 6.74 per stay.

What is the probability that 9 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0440707200

Suppose that arrivals to an emergency room occur at a rate of 5.16 per quarter hour.

What is the probability that 2 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0711038255

Suppose that car accidents at a particular intersection occur at a rate of 9.17 per month.

What is the probability that 3 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0900435440

Suppose that complications for a patient at an ICU occur at a rate of 9.02 per stay.

What is the probability that 9 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0185568089

Suppose that complications for a patient at an ICU occur at a rate of 1.36 per stay.

What is the probability that 3 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0392455867

Suppose that computer crashes occur at a rate of 8.51 per day.

What is the probability that 12 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0092607712

Suppose that computer crashes occur at a rate of 8.29 per day.

What is the probability that 4 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0981127494

Suppose that arrivals to a store occur at a rate of 3.62 per hour.

What is the probability that 3 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0515997407

Suppose that phone calls to a call center occur at a rate of 3.11 per minute.

What is the probability that 6 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0094478703

Suppose that arrivals to a store occur at a rate of 5.18 per hour.

What is the probability that 11 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0963546073

Suppose that emails to a server occur at a rate of 6.55 per second.

What is the probability that 4 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0783274339

Suppose that emails to a server occur at a rate of 6.63 per second.

What is the probability that 12 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0114282566

Suppose that arrivals to a store occur at a rate of 7.02 per hour.

What is the probability that 12 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0809768974

Suppose that arrivals to a store occur at a rate of 6.66 per hour.

What is the probability that 11 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0517013388

Suppose that arrivals to a store occur at a rate of 7.52 per hour.

What is the probability that 14 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0114666926

Suppose that phone calls to a call center occur at a rate of 2.53 per minute.

What is the probability that 6 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0147952858

Suppose that computer crashes occur at a rate of 2.45 per day.

What is the probability that 2 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0814181901

Suppose that computer crashes occur at a rate of 2.13 per day.

What is the probability that 4 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0086087171

Suppose that car accidents at a particular intersection occur at a rate of 4.21 per month.

What is the probability that 7 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0399572829

Suppose that car accidents at a particular intersection occur at a rate of 5.01 per month.

What is the probability that 3 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0820354123

Suppose that arrivals to a store occur at a rate of 5.77 per hour.

What is the probability that 5 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0774097620

Suppose that emails to a server occur at a rate of 9.81 per second.

What is the probability that 4 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0797405165

Suppose that car accidents at a particular intersection occur at a rate of 4.51 per month.

What is the probability that 5 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0616241227

Suppose that phone calls to a call center occur at a rate of 4 per minute.

What is the probability that 5 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0759939115

Suppose that arrivals to an emergency room occur at a rate of 8.19 per quarter hour.

What is the probability that 10 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0428913709

Suppose that arrivals to a store occur at a rate of 2.43 per hour.

What is the probability that 3 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0038643683

Suppose that complications for a patient at an ICU occur at a rate of 3.39 per stay.

What is the probability that 4 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0271818627

Suppose that arrivals to a store occur at a rate of 4.27 per hour.

What is the probability that 8 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0716271873

Suppose that car accidents at a particular intersection occur at a rate of 2.53 per month.

What is the probability that 7 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0158023642

Suppose that computer crashes occur at a rate of 7.97 per day.

What is the probability that 3 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0050714168

Suppose that phone calls to a call center occur at a rate of 5.69 per minute.

What is the probability that 8 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0757516808

Suppose that phone calls to a call center occur at a rate of 2.11 per minute.

What is the probability that 6 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0223940863

Suppose that car accidents at a particular intersection occur at a rate of 7.61 per month.

What is the probability that 9 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0607454143

Suppose that arrivals to an emergency room occur at a rate of 9.81 per quarter hour.

What is the probability that 17 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0505748983

Suppose that emails to a server occur at a rate of 1.92 per second.

What is the probability that 5 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0917621607

Suppose that arrivals to a store occur at a rate of 5.93 per hour.

What is the probability that 7 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0765680826

Suppose that emails to a server occur at a rate of 1.82 per second.

What is the probability that 2 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0785990973

Suppose that phone calls to a call center occur at a rate of 2.57 per minute.

What is the probability that 5 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0094440919

Suppose that emails to a server occur at a rate of 2.79 per second.

What is the probability that 4 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0260971001

Suppose that emails to a server occur at a rate of 4.75 per second.

What is the probability that 2 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0626381038

Suppose that arrivals to an emergency room occur at a rate of 6.73 per quarter hour.

What is the probability that 2 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0229791176

Suppose that car accidents at a particular intersection occur at a rate of 4.78 per month.

What is the probability that 3 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0674683882

Suppose that complications for a patient at an ICU occur at a rate of 1.89 per stay.

What is the probability that 3 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0560427959

Suppose that complications for a patient at an ICU occur at a rate of 2.47 per stay.

What is the probability that 4 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0801734616

Suppose that complications for a patient at an ICU occur at a rate of 1.94 per stay.

What is the probability that 5 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0964438054

Suppose that emails to a server occur at a rate of 9.53 per second.

What is the probability that 14 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0661029293

Suppose that complications for a patient at an ICU occur at a rate of 3.57 per stay.

What is the probability that 7 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0188623432

Suppose that arrivals to a store occur at a rate of 0.85 per hour.

What is the probability that 2 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0441538453

Suppose that arrivals to a store occur at a rate of 6.53 per hour.

What is the probability that 5 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0378672368

Suppose that car accidents at a particular intersection occur at a rate of 4.69 per month.

What is the probability that 4 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0972216402

Suppose that emails to a server occur at a rate of 4.48 per second.

What is the probability that 5 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0848976099

Suppose that arrivals to an emergency room occur at a rate of 7.91 per quarter hour.

What is the probability that 3 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0940801194

Suppose that car accidents at a particular intersection occur at a rate of 6.81 per month.

What is the probability that 6 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0415634093

Suppose that phone calls to a call center occur at a rate of 8.25 per minute.

What is the probability that 12 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0158500044

Suppose that computer crashes occur at a rate of 4.01 per day.

What is the probability that 7 computer crashes occur on a specific day?
What is the variance in the number of occurrences of computer crashes per day?

Question ID: 0095495956

Suppose that arrivals to an emergency room occur at a rate of 8.91 per quarter hour.

What is the probability that 12 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0171699773

Suppose that emails to a server occur at a rate of 7.63 per second.

What is the probability that 7 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0928843969

Suppose that complications for a patient at an ICU occur at a rate of 1.46 per stay.

What is the probability that 2 complications for the patient occur during a specific stay?
What is the variance in the number of occurrences of complications for the patient per stay?

Question ID: 0544133640

Suppose that car accidents at a particular intersection occur at a rate of 4.39 per month.

What is the probability that 8 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0137679798

Suppose that phone calls to a call center occur at a rate of 1.16 per minute.

What is the probability that 2 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0348101743

Suppose that arrivals to a store occur at a rate of 9.29 per hour.

What is the probability that 16 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0670152748

Suppose that car accidents at a particular intersection occur at a rate of 5.88 per month.

What is the probability that 2 car accidents at the particular intersection occur during a specific month?
What is the variance in the number of occurrences of car accidents at the particular intersection per month?

Question ID: 0723305299

Suppose that arrivals to a store occur at a rate of 5.68 per hour.

What is the probability that 2 arrivals to the store occur during a specific hour?
What is the variance in the number of occurrences of arrivals to the store per hour?

Question ID: 0977726229

Suppose that arrivals to an emergency room occur at a rate of 8.63 per quarter hour.

What is the probability that 6 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0977196866

Suppose that emails to a server occur at a rate of 8.58 per second.

What is the probability that 9 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0535598821

Suppose that emails to a server occur at a rate of 2.65 per second.

What is the probability that 3 emails to the server occur during a specific second?
What is the variance in the number of occurrences of emails to the server per second?

Question ID: 0735677277

Suppose that arrivals to an emergency room occur at a rate of 5.68 per quarter hour.

What is the probability that 2 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0998453000

Suppose that phone calls to a call center occur at a rate of 1.72 per minute.

What is the probability that 2 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0292708958

Suppose that phone calls to a call center occur at a rate of 5.69 per minute.

What is the probability that 9 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0890955546

Suppose that phone calls to a call center occur at a rate of 5.7 per minute.

What is the probability that 3 phone calls to the call center occur during a specific minute?
What is the variance in the number of occurrences of phone calls to the call center per minute?

Question ID: 0599962267

Suppose that arrivals to an emergency room occur at a rate of 0.98 per quarter hour.

What is the probability that 2 arrivals to the emergency room occur during a specific quarter hour?
What is the variance in the number of occurrences of arrivals to the emergency room per quarter hour?

Question ID: 0128488890

… and to a lesser extent, the expected value and variance.↩︎
Note that this assumption is not actually restrictive: if you have any $k$ items you can simply label each of the items one of the numbers between $1$ and $k$ and take $a=1$.↩︎
Or, if we forget, can lookup.↩︎
Interestingly, shuffle algorithms employed by streaming companies typically deviate far from the discrete uniform distribution. When Apple introduced shuffle to the iPod it originally had the next song be chosen as a discrete uniform over the as-yet unplayed songs. However, people found that this did not suitably feel random as maybe you would hear the same artist a few times in a row; they moved a way from an equally-likely model of selection to have people feel like it was more random.↩︎
Somewhat interestingly, this phenomenon of getting far with a small amount of effort comes up in a large number of contexts. Often referred to as the 80-20 rule the idea is that $80\%$ of results can be achieved via $20\%$ of efforts. So, for instance, approximately $80\%$ of processes in the world can be described by $20\%$ of probability distributions. This phenomenon is, itself, represented by a named distribution: the Pareto distribution. This, for me, is beautifully ironic.↩︎
The Bernoulli distribution is named after Jacob Bernoulli. The Bernoulli family was an incredibly prominent family of mathematicians from Switzerland, with their hands all over much of mathematics.↩︎
We use $\text{Bern}$ is used for Bernoulli distributions↩︎
Note, $\stackrel{iid}{\sim}$ means “independent and identically distributed according to…”↩︎
In the framing we are using here, the random variable $X$ counts the total number of trials including the trail upon which the first success was reached. Sometimes you may see this distribution parameterized slightly differently, taking $X$ to instead count the number of failures before the first success. To convert between the two framings we need only subtract $1$. There is no meaningful difference in the underlying behaviour.↩︎
Like with the geometric distribution, we have taken $X$ to represent the total number of trials considered, including the $r$ successes. There are alternative parameterizations which would count how many failures occur prior to the $r$th success, which can be viewed as the value we consider minus $r$.↩︎
Note, a royal flush is the set of cards $10$ through ace of a single suit. This is the most rare poker hand in a standard game, occurring in only $4$ ways of the $\binom{52}{5}$ total possible hands.↩︎
Depending on the type of poker being played, but it is close enough to warrant the assumption likely.↩︎
Note, if the population size is large enough drawing with or without replacement is essentially the same thing. Sometimes, in sufficiently large populations, we do not differentiate between draws with and without replacement.↩︎
What happens if you lose on sock? Why must you replace both of them? You can wear either sock on either foot. It really seems to be unnecessary that you cannot buy one at a time.↩︎
Now, $1.5$ socks can never be observed. As a result, you may say that Charles expects to see either $1$ or $2$ red socks, though, recall our way of interpreting the expected value.↩︎
The Poisson distribution gets it name from the French mathematician, Siméon Poisson, rather than from the french word for fish. Though, I suppose it is likely that the surname came from the french word for fish, so in a roundabout way, the distribution is sort of the Fish Distribution.↩︎
The Poisson distribution is interesting in that the mean and variance are always equal to one another.↩︎
As a rough rule of thumb, we would want to have $n \geq 100$ and $np \leq 10$.↩︎
More on this in the coming chapter.↩︎