6  The Expected Value, Location Summaries, and Measures of Variability

6.1 Summarizing the Location of a Distribution

Until this point in our discussions of probability we have relied upon characterizing the behaviour of a random variable via the use of probability mass functions. In some sense, a probability mass function captures all of the probabilistic behaviour of a discrete random variable. Using the mass function you are able to characterize how often, in the long run, any particular value will be observed, and answer any questions associated with this. As a result, the mass function remains a critical area of focus for understanding how random quantities behave.

However, these functions need to be explored and manipulated in order for useful information to be extracted from them. They do not summarize this behaviour effectively, as they are not intended to be a summary tool. We may wish to have numeric quantities which are able to concisely express the behaviour of a distribution. Put differently, provided with a probability mass function it is hard to immediately answer “what do we expect to happen with this random variable?” despite the fact that this is a very obvious first question.

To address questions related to our expectations, we turn towards the statistical concept of central tendency or location.

Definition 6.1 (Location (Central Tendency)) The location of a distribution is a measure of a typical value, or a central value, for that distribution. A measure of location may also be referred to as a measure of central tendency.

With measures of location we are trying to capture, with one single number, what value is expected when we make observations from the random quantity. There are many ways one might think to describe our expectations, and it is worth exploring these concepts in some detail. In particular, we want to explore how we might think to define the expected value of a distribution.¹

6.2 Deriving the Expected Value

6.2.1 The Mode

One way that we may think to define our expected value is by asking what value is the most probable. This is a question which can be directly answered using the probability mass function. The process for this requires looking at the function and determining which value for \(x\) corresponds to the highest probability. This is the value that we are most likely to see. Sometimes this procedure is fairly straightforward, sometimes it is quite complicated. Regardless of the complexity of the specific scenario, the most probable value has a straightforward interpretation. As intuitive as this may seem, this is not the value that will be used as the expected value generally. Instead, this quantity is referred to as the mode.

Definition 6.2 (Mode) The mode of a distribution is the most probable value of that distribution. Specifically, if \(X\) is a discrete random variable with mass function \(p_X(x)\), then the mode is the value of \(x\) such that \(p_X(x)\) is maximized.

Example 6.1 (Charles and Sadie Investigate Cupcake Sprinkles) Charles and Sadie have noticed that their favourite coffee shop has been experiencing less foot traffic ever since Probability Patisserie: Cupcake Conundrums has opened up next door.² This cupcake shop has been attracting many of the regular customers, though, Charles and Sadie think that it has more to do with fancy marketing than with a better product. To this end, they go into the store and workout the probability mass function for \(X\), the number of sprinkles on top of the cupcakes. They find the following \[p_X(x) = \begin{cases} 0.25 & x = 0 \\ 0.3 & x = 1 \\ 0.1 & x = 2 \\ 0.05 & x \in \{3,4,5,6,7,8,9\} \\ 0 & \text{otherwise}.\end{cases}\]

What is the mode for the number of sprinkles on the cupcakes?

Solution

The mode is the value \(x\) such that \(p_X(x)\) is a maximum. In this case the maximum occurs when \(x=1\), with \(p_X(1) = 0.3\), and so the mode of the number of sprinkles is \(1\).

While the mode is a useful quantity, and for some decisions will be the most relevant summary value, there are some major issues with it as a general measure of location. For starters, consider that our most common probability model considered until this point has been that of equally likely outcomes. Here, there is no well-defined mode.³ While the case of equally likely outcomes is a fairly strong example highlighting the issues with the mode, it need not be so dramatic to undermine its utility. It is possible for a distribution to have several modes which are quite distinct from one another, even if it’s not all values in the support.

Moreover, it is quite common for the modal value to be not particularly likely itself. Consider a random variable that can take on a million different values. If all of the probabilities are approximately \(0.000001\) then presenting the mode as the most probable value does not translate to saying that the mode is particularly probable.

Example 6.2 (Charles and Sadie Investigate Cupcake Happiness) After realizing that the cupcake shop did not provide very many sprinkles, Charles and Sadie decided to turn to the marketing material. In it, Cupcake Conundrums claims that, on a scale from \(0\) to \(100,000\) happiness points, most of their customers experience the maximum happiness after eating their cupcakes. Charles and Sadie are well aware of the ways in which these types of reports can be misleading, and so they investigate, finding the following probability mass function for the number of happiness points. \[p_X(x) = \begin{cases} \frac{x}{5,000,050,000} & x \in \{1,\dots,100 000\} \\ 0 & \text{otherwise}. \end{cases}\]

1. Is the mode reported by the company correct?
2. Is the mode an accurate depiction of the distribution in this setting?

Solution

1. Yes. Note that \(p_X(x)\) is increasing in \(x\). As a result, the mode of the distribution is the highest value that the distribution can take on, which in this case is \(x = 100,000\).

2. The mode is likely not a good indication of the distribution. Note that the maximal value happens only \(100000/5000050000\) of the time, which is a very very small value. If you look at the probability that a customer is only halfway happy, this is \(50000/5000050000\). This value is half the likelihood of the modal value, but the difference between these two probabilities is also only \(50000/5000050000 \approx 0.000001\). That is, it is only \(1\) in \(100,000\) more likely to observe perfect happiness compared with half happiness. By extension, it is only about \(2\) in \(100,000\) more likely to observe perfect happiness compared with no happiness. The mode simply is not a good indicator of behaviour in this setting.

6.2.2 The Median

If the mode has these shortcomings, what else might work? Another intuitive concept is to try to select the “middle” of the distribution. One way to define the middle would be to select the value such that, in the long run, half of observations from the distribution are beneath it and half are above it. That way, when you are told this value, you immediately know that it is equally likely to observe values on either side of this mark. This is also a particularly intuitive definition for expected value, and is important enough to be named, the median.

Definition 6.3 (Median) The median of a distribution is the value \(m\) which attempts to have \(P(X \leq m) = 0.5\) and \(P(X \geq m) = 0.5\). This value may not always exist, and so formally for discrete random variables, the median \(m\) is any value such that \(P(X \leq m) \geq 0.5\) and \(P(X \geq m) \geq 0.5\).

The median is the midpoint of a distribution and is very important for describing the behaviour of random variables. Medians are often the most helpful single value to report to indicate the typical behaviour of a distribution, and they are frequently used. When people interpret averages it is often the median that they are actually interpreting. It is very intuitive to be given a value and know that half of all realizations are above that point, and half of all realizations are below that point.

Example 6.3 (Charles and Sadie Investigate Cupcake Sprinkles (Again)) After seeing how the cupcake shop used the mode to misrepresent the happiness of its customers, Charles and Sadie worry that they may have been unfair with using the mode. As a result, they turn back to the cupcake sprinkle distribution and try to summarize it differently. Recall that the probability mass function for \(X\), the number of sprinkles on top of the cupcakes, is \[p_X(x) = \begin{cases} 0.25 & x = 0 \\ 0.3 & x = 1 \\ 0.1 & x = 2 \\ 0.05 & x \in \{3,4,5,6,7,8,9\} \\ 0 & \text{otherwise}.\end{cases}\]

What is the median number of sprinkles on the cupcakes?

Solution

Note that we are looking for a value, \(m\), such that \(P(X \geq m) \geq 0.5\) and \(P(X \leq m) \geq 0.5\). To find this we can consider the cumulative probability sums. We know that \(P(X \leq k) = \sum_{x=0}^k p_X(x)\), and as a result, stopping this value at the first time that the sum goes beyond \(0.5\) satisfies the second condition. In this case our cumulative sums are \(0.25\) then \(0.55\). As a result, \(P(X \leq 1) = 0.55 > 0.5\). If we check \(P(X \geq 1) = 1 - P(X < 1) = 1 - P(X = 0) = 0.75 > 0.5\). As a result, \(m=1\) satisfies the required conditions and is a median.

Despite the advantages of medians, they have their own drawbacks. For starters, the median can be exceptionally challenging to compute in certain settings. As a result, even when a median is appropriate, it may not be desirable if it is too challenging to determine.

Beyond the difficulties in computation, medians have a feature which is simultaneously a major benefit and a major drawback. Specifically, medians are less influenced by extreme values in the probability distribution. Consider two different distributions. The first is equally likely to take any value between \(1\) and \(10\). The second is equally likely to take any value between \(1\) and \(9\) or \(1,000,000\). In both of these settings, the median is \(5\) since \(P(X\leq 5) = 0.5\) and \(P(X \geq 5) = 0.5\). However, in the second setting we may observe a value as high as \(1,000,000\). Moreover, this value will be observed as often as the median will be.

The median, in some sense, ignores the extreme value in the probability distribution. In certain settings, this can be very desirable.⁴ Consider the distribution of household incomes. There are a few households that earn an incredibly large amount, compared to the remaining households. If you are interested in understanding the “average household”, the median may be a more appropriate measure, as those households with extreme incomes would otherwise distort the picture provided by most families. In this sense, the median’s robustness to extreme values is a positive feature of it in terms of a summary measure for distributional behaviour.

Suppose instead that you work for an insurance company and are concerned with understanding the value of insurance claims that your company will need to pay out. The distribution will look quite similar to the income distribution. Most of the probability will be assigned to fairly small claims, with a small chance of a very large one. As an insurance company, if you use the median this large claim behaviour will be smoothed over, perhaps leaving you unprepared for the possibility of extremely large payouts. In this setting, the extreme values are informative and important, and as a result the median’s robustness becomes a hindrance to correctly describing the important behaviour.⁵

Example 6.4 (Charles and Sadie Investigate Cupcake Public Relations) Charles and Sadie feel as though they may be finally catching a break when word gets around that the cupcake shop was using spoiled ingredients, making the patrons sick! The cupcake shop, in hearing this, sent their massive public relations team into damage control mode. They claimed that the median number of illnesses per week associated with the cupcake store was the same as most local food services businesses. Doing some digging, Charles and Sadie find the following two probability mass functions, for \(X\) and \(Y\), where \(X\) is the number of weekly illnesses at the cupcake shop, and \(Y\) is the number from a local business that has been around for a while. \[\begin{align*} p_X(x) &= \begin{cases} 0.1 & x = 0 \\ 0.1 & x = 1 \\ 0.35 & x = 2 \\ 0.05 & x = 3 \\ 0.4 & x = 25 \\ 0 & \text{otherwise}; \end{cases} \\ p_Y(y) &= \begin{cases} 0.45 & x = 0 \\ 0.04 & x = 1 \\ 0.5 & x = 2 \\ 0.01 & x = 3 \end{cases}. \end{align*}\]

1. What is the median of \(X\)?
2. What is the median of \(Y\)?
3. Is the claim made by the public relations team an accurate depiction of the world? Why or why not?

Solution

1. We can consider cumulative sums here again. In order we get, \(0.1\), \(0.2\), \(0.55\). This suggests that \(x=2\) is a candidate. If we check \(P(X \geq 2) = 1 - 0.2 = 0.8\), and so \(x=2\) is a median.

2. Using cumulative sums we get \(0.45\), \(0.49\), \(0.99\). Again, this gives \(x=2\) as a candidate. If we check \(P(X \geq 2) = 1 - 0.49 = 0.51\), and so \(x=2\) is a median.

3. The claim is accurate in that the median number for both establishments in \(2\). However, here the median is a bad representation for \(X\). The probability that more than \(2\) cases occur in a week at the cupcake shop is \(0.8\), compared with \(0.51\) at the local business. What’s more, the probability that \(X\) is as high as \(25\) is \(0.4\), where \(Y\) is never higher than \(3\).

Between the median and the mode we have two measures which capture some sense of expected value, each with their own set of strengths and drawbacks. Neither capture what it is that is referred to as the expected value. For this, we need to take inspiration from the median, and consider another way that we may think to find the center of the distribution.

6.2.3 The Mean

If the median gives the middle reading along the values sequentially, we may also wish to think about trying to find the center of gravity of the numbers. Suppose you take a pen, or marker, or small box of chocolates, and you wish to balance this object on a finger or an arm. To do so, you do not place the item so that half of its length sits on one side of the appendage and half on the other. You adjust the location so that half of the mass sits on either side of the appendage.

Throughout our discussion of discrete random variables we have referred to probability as mass. We use the probability mass function to generate our probability values. This metaphor can be extended when we try to find the center of the distribution. If we imagine placing a mass with weight equal to the probability mass at each value that a random variable can take on, we may ask, “where would we have to place a fulcrum to have this number line be balanced?” The answer to this question serves as another possible measure of center. It turns out that this notion of center is the one that we are all most familiar with, the simple average, or mean.

Definition 6.4 (Mean) The mean of a distribution is the center of mass of the distribution. For a random variable, \(X\) with support \(\mathcal{X}\), and probability mass function \(p_X(x)\), the mean of \(X\) is given by \[\sum_{x \in \mathcal{X}} xp_X(x).\]

It is this measure of location which ends up being called the expected value in statistics. We will use average, expected value, mean, and expectation interchangeably. In terms of notation, the expected value of a random variable \(X\) is denoted \(E[X]\). Mathematically, the expected value is desirable for many reasons, some of which we will study in more depth later on. One of these desirable features, which stands in contrast with the median, is the comparative ease with which expected values can be computed. The summation for the expected value is easy to write down, and typically can be solved (either analytically, or readily with a computer).

Example 6.5 (Charles and Sadie Investigate Cupcake Sprinkles (One Last Time)) While the median and mode number of sprinkles on the cupcakes were the same, Charles and Sadie realize that this does not end up connecting well with the total number of sprinkles given out. Perhaps customers like the possibility of getting a large number of sprinkles, if they get lucky. As a result, they decide to round out the summary of the distribution by considering the mean number of sprinkles as well. Recall that the probability mass function for \(X\), the number of sprinkles on top of the cupcakes, is \[p_X(x) = \begin{cases} 0.25 & x = 0 \\ 0.3 & x = 1 \\ 0.1 & x = 2 \\ 0.05 & x \in \{3,4,5,6,7,8,9\} \\ 0 & \text{otherwise}.\end{cases}\]

What is the mean number of sprinkles?

Solution

Recall that the mean of a distribution is given by \(E[X] = \sum_{x\in\mathcal{X}}xP_X(x)\). In this case, this results in \[\begin{align*} &\sum_{x=0}^9 xp_X(x) \\ &= 0(0.25) + 1(0.3) + 2(0.1) + (3+4+5+6+7+8+9)(0.05) \\ &= 2.6. \end{align*}\] As a result, the mean number of sprinkles used is \(2.6\). This is higher than the median and mode, but is still not particularly high.

In the case of an equally likely probability model, the expected value becomes the standard average that is widely used. Suppose that there are \(n\) options in the support with \(\mathcal{X} = \{x_1,\dots,x_n\}\). We can write \[E[X] = \sum_{i=1}^n x_i\frac{1}{n} = \frac{1}{n}\sum_{i=1}^nx_i.\] This is the formula for the average that is most commonly applied. When the probability models are more complex, the formula is not precisely the standard average – instead, it becomes a weighted average, where the weights are the probabilities.⁶ The frequency with which expected values are used make them attractive as a quick summary for the center of a distribution.

6.2.4 How is the Mean “Expected”?

While the mean provides a useful, intuitive measure of center of the distribution, it is perhaps counterintuitive to name it the “expected value.” To understand the naming convention it is easiest to consider the application which has likely spurred more development of statistics and probability than any other: gambling.

Suppose that there is some game of chance that can pay out different amounts with different probabilities. A critical question for a gambler in deciding whether or not to play such a game is “how much can I expect to earn, if I play?” This is crucial to understanding, for instance, how much you should be willing to pay to participate, or if you are the one running the game, how much you should charge to ensure that you make a profit.

If you want to understand what you expect to earn, the intuitive way of accomplishing this is to weight each possible outcome by how likely it is to occur. This is exactly the expected value formula that has been provided, and so the expected value can be thought of as the expected payout of a game of chance where the outcomes are payouts corresponding to each probability.

Cost for a Game of Chance

Suppose that a game of chance is being run. It will cost \(\$m\) to play, and the game will pay out values from \(\mathcal{X}\), according to a random variable \(X\) with probability mass function \(p_X(x)\). The question that we want to know is what should the value be for \(m\), such that, in the long term, a player playing the game will earn no money?

Note that if \(X=x\) then a player playing the game will earn \(x - m\) for that play, and this will happen with probability \(p_X(x)\). Thus, in the long run, in \(p_X(x)\) proportion of games the player earns \(x-m\). If the player plays \(N\) games, then as \(N\to\infty\), the total contribution from these winnings will be \((x-m)\cdot N\cdot p_X(x)\). If we add up this contribution for all possible results, \(x\), we get \[\begin{align*} \sum_{x\in\mathcal{X}} N(x-m)p_X(x) &= N\left[\sum_{x\in\mathcal{X}}xp_X(x) - \sum_{x\in\mathcal{X}} mp_X(x)\right] \\ &= N\left[\sum_{x\in\mathcal{X}}xp_X(x) - m\sum_{x\in\mathcal{X}}p_X(x)\right] \\ &= N\left[E[X] - m\right]. \end{align*}\] Thus, in the long run, the total that the player wins, as \(N\to\infty\) will be \(N(E[X] - m)\). Thus, in order for the long run earnings to be zero, \(m\) should be set to be equal to \(E[X]\).

If \(m\) is set to be \(0\), then per game the player expects to earn \(E[X]\). This also represents the cost at which a rational actor should be willing to pay to participate. If a game of chance costs more than the expected value to play, in the long run you will lose money. If a game of chance costs less than the expected value, in the long run you will earn money. It is hard to overstate the utility of gambling in developing probability theory, and as such these types of connections are expected.

To interpret the expected value of a random variable, one possibility is using the intuition that we used to derive the result. Notably, the expected value is the center of mass of the distribution, where the masses correspond to probabilities. This means that it is not necessarily an actual central number over the range, but rather that it sits in the weighted middle. While this interpretation is useful in many situations, there are times where the point of balance is a less intuitive description. For these, it can sometimes be useful to frame the expected value as the long term simple average from the distribution.

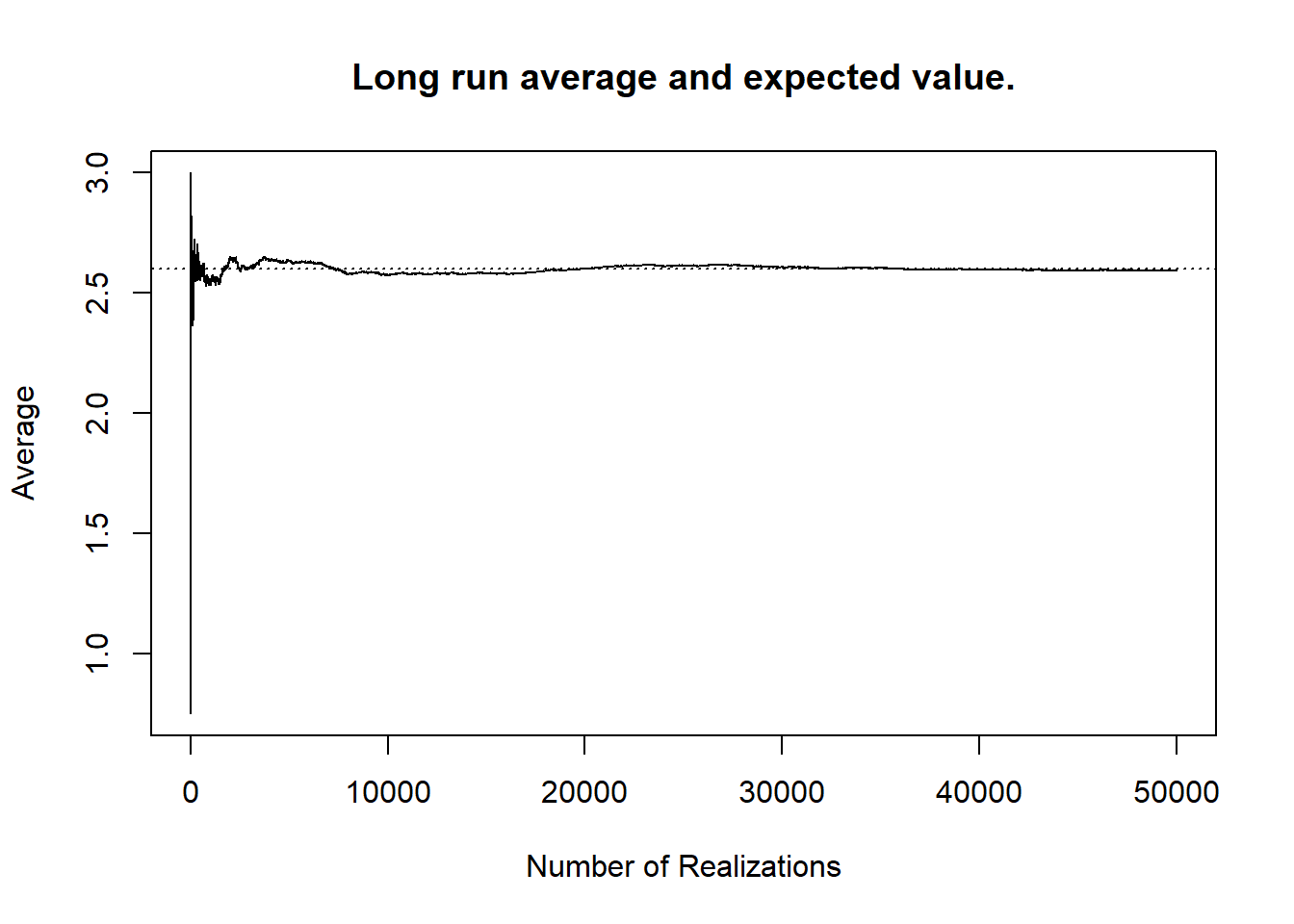
If we imagine observing many independent and identically distributed random variables, then as the number of samples tends to infinity, the expected value of \(X\) and the simple average will begin to coincide with one another. That is the distance between \(E[X]\) and \(\frac{1}{n}\sum_{i=1}^n X_i\) will shrink to \(0\). As a result, we can view the expected value as the average over repeated experiments. This interpretation coincides nicely with the description based on games of chance. Specifically, if you were to repeatedly play the same game of chance, the average payout per game will be equal to the expected value, if you play for long enough.

Figure 6.1: This plot produces 50000 realizations of the random variable described in Example 6.5. As computed in the example, the expected value is 2.6. As many repeated observations are averaged, the empirical average converges to this computed value.

6.3 Which Measure of Central Tendency Should be Used?

Where the median demonstrated robustness against extreme values in the distribution, the mean does not. For instance, if we consider the distribution of incomes across a particular region, the mean will be much higher than the median, since those families with exceptionally high incomes will not be smoothed over as they were with medians. In this case, the lack of robustness for the expected value will render the mean a less representative summary for the true behaviour of the random quantity.

To see this concretely consider a random variable which with equal probability takes a value between \(1\) and \(9\). This will have \(E[X] = 5\). Now, if the \(9\) is made to be \(1,000,000\), the expected value will now be \(E[X] = 111115.\dot1\). This is a far cry from the median which does not change from \(5\) in either case. This lack of robustness is desirable in the event of the insurance example from the median discussion, but will be less desirable in other settings.

The mean, median, and mode are the three standard measures of central tendency. They are single values which describe the standard behaviour of a random quantity. Each of the three has merits as a measure, and each has drawbacks for certain settings. The question of which to use and when depends primarily on the question of interest under consideration, rather than on features of the data alone.⁷ Often, presenting more than one measure can give a better sense of the distributional behaviour that any one individual will.

Example 6.6 (Charles and Sadie Reflect on the Cupcake Adventures) Charles and Sadie decide it is worth stepping back and summarizing all that has happened with regards to their cupcake adventures, trying to ensure that distributions are always summarized fairly.

1. For the number of sprinkles per cupcake is the mean, median, or mode the best measure of central tendency?
2. For the amount happiness in customers, is the mean, median, or mode the best measure of central tendency?
3. For the number of customers who become ill eating at establishments, is the mean, median, or mode the best measure of central tendency?

Solution

1. There is an argument that any of the measures here could work the best, it would depend on the individual’s preferences. The mode makes a lot of sense as, if you are a regular customer, the mode is what you will experience day-to-day; most days you will have the modal number of sprinkles. The median may make sense as it provides a benchmark for measuring what constitutes a lot of sprinkles and a little. Half of the time you’ll end up with a more sprinkled donut, half the time a less. The mean would be particularly interesting to note for the store owners themselves, since the mean is directly tied to totals: if the store knows that they sell \(100\) cupcakes per day, most days, then they also can expect to use \(100\) times the mean number of sprinkles in a day. This is helpful for planning.

2. The median is likely the most useful measure in this setting. The mode could be useful if happiness were not measured on a \(100,000\) point scale. The mean is likely a less relevant value here as we are not particularly concerned with the total happiness, and if there was a large skew or major outliers in this distribution, we would want to determine where the majority fall. This is more analogous to the income example rather than the insurance example.

3. In this case either the mode or mean are likely the best gauges. Here we do care about totals, and in particular, we do not want to smooth over outliers. It is very relevant if sometimes a lot of individuals become ill after eating an establishment, and the median would hide this information.

Despite the utility of all three measures, the expected value holds a place of more central importance in probability and statistics. A lot of this has to do with further mathematical properties of the mean. Because of its central role, it is worth studying the expected value in some more depth.

6.4 Expected Values of Functions of Random Variables

Sometimes the value of a random variable needs to be mapped through a function to give the value which is most relevant to us. Consider, for instance, a situation wherein the side lengths of boxes being manufactured by a specific supplier are random, due to incorrectly calibrated tolerances in the machines. The resulting boxes are perfect cubes. Suppose we are interested in the volume of the produced box not the side length. If a box has side length \(x\), then its volume will be \(x^3\), and so we may desire some way of computing \(E[X^3]\) rather than \(E[X]\).

Generally, for a function \(g(X)\), we may want to compute \(E[g(X)]\). It is important to recognize that \(E[g(X)] \neq g(E[X])\). This is a common mistake.⁸ If we are unable to apply the function to the expected value, then the question of how to compute the expected value remains. Instead of applying the function to overall expected value, instead, we apply the function to each value in the defining relationship for the expected value. That is, \[E[g(X)] = \sum_{x\in\mathcal{X}} g(x)p_X(x).\] This is sometimes referred to as the “law of the unconscious statistician,” a name which may be aggressive enough to help remember the correct way to compute the expectation.⁹

The Law of the Unconscious Statistician

The law of the unconscious statistician (LOTUS) states that, for a random variable \(X\), if we wish to find \(E[g(X)]\), then we compute \[E[g(X)] = \sum_{x\in\mathcal{X}} g(x)p_X(x).\]

Example 6.7 (The Happiness Scale Inversion) Charles and Sadie have made really great strides working to protect their favourite coffee shop from the new cupcake store. One day when digging through the material more, they realize that the happiness report produced by the company is even less accurate than they had originally reported! The company reported the following probability mass function for happiness points \[ p_X(x) = \begin{cases} \frac{x}{5,000,050,000} & x \in \{1,\dots,100 000\} \\ 0 & \text{otherwise}. \end{cases}\] Charles and Sadie track down the source of this expression and they find that, in fact, this does not measure happiness points at all. Instead, the number of happiness points is a function of \(X\), specifically, \(Z = 1/X\).

1. What is the expected value of \(X\)? Note, it may be helpful to recall that \(\sum_{x=1}^{k} x^2 = \frac{k(k+1)(2k+1)}{6}\).
2. What is the expected value of \(Z\)?

Solution

1. Using directly the formula for \(E[X]\) gives \[\begin{align*} E[X] = \sum_{x=1}^{100000} xp_X(x) &= \sum_{x=1}^{100000} x\frac{x}{5000050000} \\ &= \frac{1}{5000050000}\sum_{x=1}^{100000}x^2 \\ &= \frac{1}{5000050000}\cdot\frac{100000(100000+1)(2(100000)+1)}{6} \\ &= 66 667. \end{align*}\]

2. Applying the law of the unconscious statistician, gives \[\begin{align*} E[Z] = E[1/X] = \sum_{x=1}^{100000} \frac{1}{x}p_X(x) &= \sum_{x=1}^{100000} \frac{1}{x}\frac{x}{5000050000} \\ &= \frac{1}{5000050000}\sum_{x=1}^{100000} 1 \\ &= \frac{100000}{5000050000} \\ &= \frac{2}{100001}. \end{align*}\]

These functions applied to random variables are often thought of as “transformations” of the random quantities. For instance, we transformed a side length into a volume. While the law of the unconscious statistician will apply to any transformation for a random variable, we can sometimes use shortcuts to circumvent its application. In particular, when \(g(X) = aX + b\), for constant numbers \(a\) and \(b\), we can greatly simplify the expected value of the transformation. To see this note \[\begin{align*} E[aX + b] &= \sum_{x\in\mathcal{X}}(ax + b)p_X(x) \\ &= \sum_{x\in\mathcal{X}}axp_X(x) + bp_X(x) \\ &= a\sum_{x\in\mathcal{X}}xp_X(x) + b\sum_{x\in\mathcal{X}}p_X(X) \\ &= aE[X] + b. \end{align*}\] That is, in general, we have that \(E[aX + b] = aE[X] + b\). Note that part of the property of the linearity of expectation that we can immediately see if that the expected value of any constant is always that constant. If we take \(a = 0\), then we see that \(E[aX + b] = E[b] = b\). Thus, any time that we need to take the expected value of any constant number, we know that it is just that number.

This is particularly useful as linear transformations like \(aX+b\) arise very commonly. For instance, most unit conversions are simple linear combinations. If a random quantity is measured in one unit then this result can be used to quickly convert expectations to another.

Example 6.8 (Sadie’s Trip to America) Sadie has recently returned from a long trip to America. The trip was long enough that temperatures measured in Fahrenheit started to make sense. When Sadie and Charles begin to talk about the weather, Charles brings up the temperature distribution of a possible summer vacation spot. Unfortunately for Sadie, these temperatures are all in Celsius. The distribution Charles provides is \[p_X(x) = \begin{cases} 0.1 & x \in \{10, 11, 12, 13, 14\} \\ 0.05 & x \in \{15, 16, 17, 18, 19, 20, 21, 22, 23, 24\} \\ 0 & \text{otherwise} \end{cases}\]

1. What is the expected temperature, in Celsius?
2. Supposing that the temperature in Fahrenheit is given by \(Y = 1.8X + 32\), what is the expected temperature in Fahrenheit?

Solution

1. Here we find \[\begin{align*} \sum_{x=10}^{24} xp_X(x) &= 0.1\sum_{x=10}^{14}x + 0.05\sum_{x=15}^{24}x \\ &= 15.75. \end{align*}\]

2. Since \(E[X] = 15.75\) then \(E[Y] = E[1.8X + 32] = 1.8E[X] + 32 = 60.35\).

This type of linear transformation also frequently comes up with games of chance and payouts, or with scoring more generally.¹⁰ Beyond being linear over simple transformations, summations in general behave nicely with expectations. Specifically, for any quantities separated by addition, say \(g(X) + h(X)\), the expected value will be the sum of each expected value. Formally, \[\begin{align*} E[g(X) + h(X)] &= \sum_{x\in\mathcal{X}} (g(x) + h(x))p_X(x) \\ &= \sum_{x\in\mathcal{X}} g(x)p_X(x) + h(x)p_X(x) \\ &= \sum_{x\in\mathcal{X}} g(x)p_X(x) + \sum_{x\in\mathcal{X}} h(x)p_X(x) \\ &= E[g(X)] + E[h(X)]. \end{align*}\]

Behaving well under linearity is one of the very nice properties of expectations. It will come in useful when dealing with a large variety of important quantities, and as we will see shortly, this linearity will also extend to multiple different random quantities.

Measures of central tendency are important to summarize the behaviour of a random quantity. Whether using the mean, median, or mode, these measures of location describe, on average, what to expect from observations of the random quantity. However, understanding a distribution requires understanding far more than simply the measures of location. As was discussed previously, the probability mass function captures the complete probabilistic behaviour of a discrete random variable, it is only intuitive that some information would be lost with a single numeric summary.

Equal Location Across Different Distributions

Consider the following three distributions for three random variables, \(X\), \(Y\), and \(Z\): \[\begin{align*} p_X(x) = \begin{cases} 0.25 & x = -1 \\ 0.5 & x = 0 \\ 0.25 & x = 1 \\ 0 & \text{otherwise}. \end{cases} \quad p_Y(y) &= \begin{cases} 0.05 & x = -5 \\ 0.1 & x = -4 \\ 0.1 & x = -3 \\ 0.1 & x = -2\\ 0.1 & x = -1\\ 0.15 & x = 0 \\ 0.1 & x = 1\\ 0.1 & x = 2\\ 0.1 & x = 3\\ 0.1 & x = 4 \\ 0.05 & x = 5 \\ 0 & \text{otherwise}. \end{cases} \quad p_Z(z) = \begin{cases} 0.25 & x = -400 \\ 0.5 & x = 0 \\ \frac{1}{3196} & x \in \{1,\dots,799\}\\ 0 & \text{otherwise}. \end{cases}. \end{align*}\]

In each of these distributions we have the mean, median, and mode all equalling \(0\).¹¹ However, even just from a quick glance, these distributions are all very, very differently behaved. The location summaries here clearly miss much of the important information about these different distributions. Spend some time trying to think of the ways in which they differ from one another, and see if you can determine what is missing from relying solely on measures of location.

6.5 Summarizing the Variability of a Random Variable

A key characteristic of the behaviour of a random variable which is not captured by the measures of location is the variability of the quantity. If we imagine taking repeated realizations of a random variable, the variability of the random variable captures how much movement there will be observation to observation. If a random variable has low variability, we expect that the various observations will cluster together, becoming not too distant from one another. If a random variable has high variability, we expect the observations to jump around each time.

6.5.1 The Range

Just as was the case with measures of location, there are several measures of variability which may be applicable in any given setting. One fairly basic measure of this variability is the range of possible values: what is the highest possible value, what is the lowest possible value, and how much distance is there between those two points?

Definition 6.5 (Range) For a random variable, \(X\), the range of the random variable is defined as \(\text{Range}(X) = \max(X) - \min(X)\). That is, it is the distance between the maximum value that the random variable can take on, and the minimum value that the random variable can take on. Sometimes the range is reported with these outpoints explicitly specified.

This is a fairly intuitive notion, and is particularly useful in the equal probability model over a sequence of numbers. Consider dice. Dice are typically defined by the range of values that they occupy, say \(1\) to \(6\), or \(1\) to \(20\). Once you know the values present on any die, you have a sense for how much the values can move observation to observation.

Example 6.9 (Charles and Sadie Explore Ice Cream Flavors) Charles and Sadie have decided to spend their sunny afternoon exploring various ice cream flavors at their local parlor, Symmetric Scoops. They notice that Scoops Galore offers a wide variety of flavors, from classic vanilla to exotic dragon fruit swirl. Intrigued by the selection, they decide to investigate the probability distribution of a random variable, \(Y\), representing the number of unique flavors a customer selects.

After discreetly observing several customers, Charles and Sadie jot down their findings: \[ p_Y(y) = \begin{cases} 0.2 & y = 1 \\ 0.35 & y = 2 \\ 0.3 & y = 3 \\ 0.15 & y = 4 \\ 0 & \text{otherwise} \end{cases} \]

What is the range of the random variable \(Y\), representing the number of unique ice cream flavors a customer selects at Scoops Galore?

Solution

Looking at the defining relationship for this random variable, we can see that the maximum value the distribution can take on is \(4\) (with probability \(0.15\)) and the minimum value is \(1\) (with probability \(0.2\)). As a result, we say that \(\text{Range}(Y) = 4 - 1 = 3\).

While the range is an important measure to consider to determine the behaviour of a random variable, it is a fairly crude measurement. It may be the case that, while the extreme values are possible, they are sufficiently unlikely so as to come up very infrequently and not remain representative of the likely spread of observations. Alternatively, many random variables have a theoretically infinite range. In these cases, providing the range will likely not provide much utility.

Example 6.10 (Charles and Sadie Explore Ice Cream Flavors, Again) Having had so much fun at Symmetric Scoops the first time, Charles and Sadie return once more to continue to investigate customers behaviour. When they arrive they notice a temporary promotion going on, which happens on one randomly selected Sunday a year, where customers can buy a Mega Sunda(y)e Extravaganza, a wonderfully extravagant creation that features scoops from all \(50\) flavours on offer. Working on this today they find the following probability mass function for \(Y\). \[ p_Y(y) = \begin{cases} 0.2 & y = 1 \\ 0.35 & y = 2 \\ 0.3 & y = 3 \\ 0.145 & y = 4 \\ 0.005 & y = 50 \\ 0 & \text{otherwise} \end{cases} \]

What is the range of the random variable \(Y\) now? Does this accurately represent the dispersion we expect from \(Y\)?

Solution

Looking at the defining relationship for this random variable, we can see that the maximum value the distribution can take on is \(50\) (with probability \(0.005\)) and the minimum value is \(1\) (with probability \(0.2\)). As a result, we say that \(\text{Range}(Y) = 50 - 1 = 49\). This does not accurately represent the dispersion of the random variable. Not only do very few customers order this when it is available, it is also almost never available. As a result, the maximum value (while possible) is not reflective of the usual behaviour of this random quantity, and this displays one of the concerns with the range as a measure of spread.

6.5.2 The Interquartile Range

To remedy these two issues, we may think of techniques to modify the range. Instead of taking the minimum and maximum possible values, we can instead consider ranges of values which remain more plausible. A common way to do this is to extend our concept of a median beyond the half-way point. The median of a random variable \(X\), is the value, \(m\), such that \(P(X \leq m) = 0.5\)¹². While there is good reason to care about the midpoint, we can think of generalizing this to be any probability.

That is, we could find a number \(z\), such that \(P(X \leq z) = 0.1\). We could then use this value to conclude that the probability of observing a value less than \(z\) is \(10\%\). These values are referred to, generally, as percentiles and they are the natural extension of medians.

Definition 6.6 (Percentiles) The \(100p\)th percentile (e.g., \(70\)th percentile for \(p=0.7\), or \(20\)th percentile for \(p=0.20\)), is denoted \(\zeta(p)\) and is the value such that \(P(X \leq \zeta(p)) = p\). Thus, the median is given by \(\zeta(0.5)\) and is also called the \(50\)th percentile.¹³

Example 6.11 (Perplexed at the Ice Cream Parlour) Charles and Sadie remained somewhat disappointed by their lack of ability to accurately capture the behaviour of a random variable using the range. To this end, they spend a lot more time at the ice cream parlor, and come up with, what they believe, is the correct probability mass function for how many flavours customers order, in total. \[ p_Y(y) = \begin{cases} 0.25 & y = 1 \\ 0.25 & y = 2 \\ 0.1 & y = 3 \\ 0.05 & y = 4 \\ 0.05 & y = 5 \\ 0.05 & y = 6 \\ 0.15 & y = 7 \\ 0.05 & y = 8 \\ 0.04 & y = 9 \\ 0.005 & y = 10 \\ 0.005 & y = 50 \\ 0 & \text{otherwise} \end{cases} \]

Using this probability mass function, find \(\zeta(0.25)\), \(\zeta(0.5)\), \(\zeta(0.75)\), and \(\zeta(0.99)\). What do each of these values mean?

Solution

1. \(\zeta(0.25)\) is found by looking for \(P(Y \leq \zeta(0.25)) = 0.25\). We note that \(P(Y \leq 1) = P(Y = 1) = 0.25\), and so \(\zeta(0.25) = 1\). This means that there is a \(25\%\) chance that a randomly selected individual will order \(1\) or fewer flavours.
2. \(\zeta(0.5)\) is found by looking for \(P(Y \leq \zeta(0.5)) = 0.25\). Note that \(P(Y \leq 2) = P(Y = 1) + P(Y = 2) = 0.5\), and so \(\zeta(0.5) = 2\). This means that \(50\%\) of customers order \(2\) or fewer flavours, and \(50\%\) of customers order more than \(2\) flavours.
3. \(\zeta(0.75)\) is found by looking for \(P(Y \leq \zeta(0.75)) = 0.75\). Note that we can continue the cumulative sums from the probability mass function. This gives, in order, \(0.25, 0.5, 0.6, 0.65, 0.7, 0.75, 0.9, 0.95, 0.99, 0.995, 1\). As a result, \(P(Y \leq 6) = 0.75\) and so \(\zeta(0.75) = 6\). This means that \(75\%\) of customers order \(7\) or fewer flavours (the remaining \(25\%\) order more than \(7\)).
4. \(\zeta(0.99)\) can be found through the same cumulative sums as in (c). This is given by \(y = 9\), such that \(P(Y \leq 9) = 0.99\), so \(\zeta(0.99) = 9\). This means that \(99\%\) of individuals order \(9\) or fewer flavours.

We can leverage percentiles to remedy some of the issues with the range as a measure of variability. Framed in terms of percentiles, the minimum value is \(\zeta(0)\), and the maximum value is \(\zeta(1)\). Instead of considering the extreme endpoints, we can consider the difference between more moderate percentiles. Doing so allows us to overcome the major concerns outlined with the range. If we take \(\zeta(p_1)\) and \(\zeta(p_2)\), for \(p_1 < p_2\), then the difference between \(\zeta(p_2) - \zeta(p_1)\) can be seen as a measure of variability, analogous to the range.

The most common choices would be to take \(\zeta(0.25)\) and \(\zeta(0.75)\), the \(25\)th and \(75\)th percentiles, respectively. These are also referred to as the first and third quartiles, respectively. They are named as, taking \(\zeta(0.25)\), \(\zeta(0.5)\) and \(\zeta(0.75)\), the distribution is cut into quarters.

With the first and third quartiles computed, we can compute the interquartile range, which is given by \(\zeta(0.75)-\zeta(0.25)\).

Definition 6.7 (Interquartile Range (IQR)) The interquartile range, or IQR, is defined as \(\zeta(0.75) - \zeta(0.25)\), the difference between the third and first quartiles. It is a measure of spread, and is typically denoted as \(\text{IQR} = Q3 - Q1\), where \(Q\) stands for quartiles.

Like the range, the IQR gives a measure of how much spread there tends to be in a distribution. Unlike the range, however, we can be more certain that both the first and third quartiles are reasonable values around which repeated observations of the random variable would be observed. Specifically, there is a probability of \(0.5\) that a value between the first and third quartile will be observed. The larger the \(\text{IQR}\), the more spread out these moderate observations will be, and as a result, the more variable the distribution is.

Example 6.12 (Addressing the Ice Cream Perplexity) Having understood many of the percentiles of the distribution of ice cream flavours ordered at Symmetric Scoops, Charles and Sadie decide to have another shot at capturing the spread. Recall that the probability mass function for \(Y\), the number of ice cream flavours ordered by a customer, is given by \[ p_Y(y) = \begin{cases} 0.25 & y = 1 \\ 0.25 & y = 2 \\ 0.1 & y = 3 \\ 0.05 & y = 4 \\ 0.05 & y = 5 \\ 0.05 & y = 6 \\ 0.15 & y = 7 \\ 0.05 & y = 8 \\ 0.04 & y = 9 \\ 0.005 & y = 10 \\ 0.005 & y = 50 \\ 0 & \text{otherwise} \end{cases} \]

What is the interquartile range for this population? How does this compare to the range?

Solution

We know that \(\zeta(0.25) = 1\) and \(\zeta(0.75) = 6\). As a result, the \(\text{IQR} = 6 - 1 = 5\). By contrast, the range is given by \(50 - 1 = 49\). It is incredibly rare to observe a customer ordering \(50\) flavours, as a result, using \(5\) is a better measure of spread of the distribution. To see this, we could consider plotting a histogram (more on these later on) that show the number of customers who order each type, and then intuitively as for a good measure of how spread out the data are.

6.5.3 The Variance and Mean Absolute Deviation

Both the range and the interquartile range give a sense of the variation in the distribution irrespective of the measures of location for that distribution. Another plausible method for assessing the variability of a distribution is to assess how far we expect observations to be from its center. Intuitively, if observations of \(X\) are near the center with high probability, then the distribution will be less variable than if the average distance to the center is larger.

This intuitive measure of variability is useful for capturing the behaviour of a random variable, particularly when paired with a measure of location. However, we do have to be careful: not all measures of dispersion based on this notion will be useful. Consider the most basic possibility, \(X - E[X]\). We might ask, for instance, what is the expected value of this quantity. If we take \(E[X - E[X]]\) then note that this a linear combination in expectation since \(E[X]\) is just some number. Thus, \(E[X-E[X]] = E[X] - E[X] = 0\). In other words, the expected difference between a random variable and its mean is exactly \(0\). We thus need to think harder about how best to turn this intuition into a useful measure of spread.

The issue with this procedure is that some realizations are going to be below the mean, making the difference negative, and some will be above the mean, making the difference positive. Our defining relationship for the mean relied on balancing these two sets of mass. However, when discussing the variability of the random variable, we do not much care whether the observations are lower than expected or higher than expected, we simply care how much variability there is around what is expected. To remedy this, we should consider only the distance between the observation and the expectation, not the sign. That is, if \(X\) is \(5\) below \(E[X]\) we should treat that the same as if \(X\) is \(5\) above \(E[X]\).

There are two common ways to turn value into its magnitude in mathematics generally: squaring the number and using absolute values. Both of these tactics are useful approaches to defining measures of spread, and they result in the variance when using the expected value of the squared deviations, and the mean absolute deviation when using the absolute value. While \(E[|X-E[X]|]\) is perhaps the more intuitive quantity to consider, generally speaking it will not be the one that we use.

Definition 6.8 (Variance) The variance of a random variable, typically denoted \(\text{var}(X)\), is given by the expected value of the squared deviations of a random variable from its mean. That is, \[\text{var}(X) = E\left[(X - E[X])^2\right].\]

Definition 6.9 (Mean Absolute Deviation) The mean absolute deviation of a random variable, typically denoted \(\text{MAD}(X)\), is given by the expected value of the absolute value of the deviations of a random variable from its mean. That is, \[\text{MAD}(X) = E\left[|X - E[X]|\right].\]

In general when we need a positive quantity in mathematics it will typically be preferable to consider the square to the absolute value.¹⁴ The variance is the central measure of deviation for random variables. When discussing the variability of a random variable, it will almost universally be in reference to the variance.

Note that if we take \(g(X) = (X-E[X])^2\), then the variance of \(X\) is the expected value of a transformation. We have seen that to compute these we apply the law of the unconscious statistician, and substitute \(g(X)\) into the defining relationship for the expected value, which for the variance gives \[\text{var}(X) = \sum_{x\in\in\mathcal{X}} (x-E[X])^2p_X(x).\] In order to compute the variance, we must also find the mean as the function \(g(X)\) relies upon this value.

Example 6.13 (Variation in the Number of Ice Cream Flavours Ordered) Noting how different the range and IQR were of the distribution of number of different flavours ordered by customers at the ice cream parlour, Charles and Sadie decide to turn to the variance and mean absolute deviation to try understand the distribution’s variability once-and-for-all. Recall that the probability mass function for \(Y\), the number of ice cream flavours ordered by a customer, is given by \[ p_Y(y) = \begin{cases} 0.25 & y = 1 \\ 0.25 & y = 2 \\ 0.1 & y = 3 \\ 0.05 & y = 4 \\ 0.05 & y = 5 \\ 0.05 & y = 6 \\ 0.15 & y = 7 \\ 0.05 & y = 8 \\ 0.04 & y = 9 \\ 0.005 & y = 10 \\ 0.005 & y = 50 \\ 0 & \text{otherwise} \end{cases} \]

Find the variance and the mean absolute variation for this distribution.

Solution

For both \(\text{var}(Y)\) and \(\text{MAD}(Y)\) we require the expected value of \(Y\). To this end note that \[\begin{multline*}E[Y] = (0.25)(1) + (0.25)(2) + (0.1)(3) + (0.05)(4) + (0.05)(5) + (0.05)(6) + (0.15)(7) \\ + (0.05)(8) + (0.04)(9) + (0.005)(10) + (0.005)(50) = 3.91.\end{multline*}\]

Then, it can be useful to define a table with the probabilities, absolute, and squared deviations, so that the summations can be made easier.

\(Y\)	\(p_Y(y)\)	\((Y - E[Y])^2\)	\(|Y - E[Y]|\)
\(1\)	\(0.25\)	\(8.4681\)	\(2.91\)
\(2\)	\(0.25\)	\(3.6481\)	\(1.91\)
\(3\)	\(0.1\)	\(0.8281\)	\(0.91\)
\(4\)	\(0.05\)	\(0.0081\)	\(0.09\)
\(5\)	\(0.05\)	\(1.1881\)	\(1.09\)
\(6\)	\(0.05\)	\(4.3681\)	\(2.09\)
\(7\)	\(0.15\)	\(9.5481\)	\(3.09\)
\(8\)	\(0.05\)	\(16.7281\)	\(4.09\)
\(9\)	\(0.04\)	\(25.9081\)	\(5.09\)
\(10\)	\(0.005\)	\(37.0881\)	\(6.09\)
\(50\)	\(0.005\)	\(2124.2881\)	\(46.09\)

With this table we can compute both the variance and mean absolute deviation by taking the second column times by the third, and adding up those results (for the variance) and the second column times the fourth, and adding up those results (for the MAD). Doing so results in \(\text{var}(Y) = 17.5019\) and \(\text{MAD}(Y) = 2.592\).

6.5.4 Standard Deviation

The higher that an individual random variable’s variance is, the more spread we expect there to be in repeated realizations of that quantity. Specifically, the more spread out around the mean value the random variable will be. A random variable with a low variance will concentrate more around its mean value than one with a higher variance. One confusing part of the variance of a random variable is in trying to assess the units. Suppose that a random quantity is measured in a particular set of units – dollars, seconds, grams, or similar. In this case, our interpretations of measures of location will all be in the same units, which aids in drawing connections to the underlying phenomenon that we are trying to study. However, because the variance is squared, we cannot make the same extensions to it. Variance is not measured in the regular units, but in the regular units, squared.

Suppose you have a random time being measured, perhaps the reaction time for some treatment to take effect in a treated patient. Finding the mean or median will give you a result that you can read off in seconds. The range and interquartile range both give you the spread in seconds. However, if you work out the variance of this quantity it will be measured in seconds squared – a unit that is challenging to have much intuition about. To remedy this we will often use a transformed version of the variance, called the standard deviation, returning the units to be only the original scale.

Definition 6.10 (Standard Deviation) The standard deviation of a random variable is the square root of the variance, which is to say \[\text{SD}(X) = \sqrt{\text{var}(X)}.\]

We do not often consider computing the standard deviation directly, and so will most commonly refer to the variance when discussing the behaviour of a random variable, but it is important to be able to move seamlessly between these two measures of spread.

Example 6.14 (Variation in the Number of Ice Cream Flavours Ordered, the Finale) Having realized that the IQR and range are not directly comparable to the variance, as they are measured in different units, Charles and Sadie decide to end their investigation in the variability of the number of ice cream flavours ordered by calculating the standard deviation of \(Y\). Recall that the probability mass function for \(Y\), the number of ice cream flavours ordered by a customer, is given by \[ p_Y(y) = \begin{cases} 0.25 & y = 1 \\ 0.25 & y = 2 \\ 0.1 & y = 3 \\ 0.05 & y = 4 \\ 0.05 & y = 5 \\ 0.05 & y = 6 \\ 0.15 & y = 7 \\ 0.05 & y = 8 \\ 0.04 & y = 9 \\ 0.005 & y = 10 \\ 0.005 & y = 50 \\ 0 & \text{otherwise} \end{cases}. \]

What is the standard deviation of this random variable?

Solution

The standard deviation is given by the square root of the variance. This is given by \(\sqrt{17.5019} = 4.18353\).

Example 6.15 (The Dolphin Olympics) Sadie and Charles, on a trip to a beach in a particularly quirky town, find themselves watching the dolphin Olympics. These are a set of games put on by the local dolphin populations where they see how high they can jump from the water, and how many flips they can do while they do it. Charles and Sadie get to work determining the probability distributions related to the heights and the number of flips, with Sadie taking the heights and Charles taking the number of flips. At the end of the day they are discussing their findings and Sadie indicates that the standard deviation of the height that was jumped was \(1.6m\). Charles is intrigued, saying, “I could have sworn that there was more variation in the jump heights than in the number of flips, but the variance of the flips was \(2.56\), greater than the variability in the heights!”

Is Charles correct? Why or why not?

Solution

Charles has compared the standard deviation of the first quantity to the variance of the second. We must compare the same measure, and as a result, conclude that the variance of the heights was \(1.6^2 = 2.56\), exactly the same as the second.

6.6 Computing the Variance

When computing the variance of a random quantity, we often use a shortcut for the formula, \[\text{var}(X) = E[X^2] - E[X]^2.\] Generally, this is moderately more straightforward to calculate since \(X^2\) is an easier transformation than \((X-E[X])^2\). This identity will come back time and time again, with a lot of versatility in the ways that it can be used. Typically, when a variance is needed to be calculated the process is to simply compute \(E[X]\) and \(E[X^2]\), and then apply this relationship.

Proof of the Variance Identity

To determine the variance identity, we need only remember the definition of the variance (being \(E[(X-E[X])^2]\)), and then use summation techniques to manipulate the expression. To this end consider, \[\begin{align*} \text{var}(X) &= \sum_{x\in\mathcal{X}} (x-E[X])^2p_X(x) \\ &= \sum_{x\in\mathcal{X}} (x^2 - 2xE[X] + E[X]^2)p_X(x) \\ &=\sum_{x\in\mathcal{X}} x^2p_X(x) - 2E[X]\sum_{x\in\mathcal{X}}xp_X(x) + E[X^2]\sum_{x\in\mathcal{X}}p_X(x)\\ &= E[X^2] - 2E[X]E[X] + E[X]^2\\ &= E[X^2] - E[X]^2. \end{align*}\]

Example 6.16 (Choosing the Outcome of a Die) Charles and Sadie come across a new game of chance involving the rolling of a die. In it a player chooses a number between \(1\) and \(6\). They then roll a die (up to) \(6\) times. If they get their chosen number on the first throw for the first time, they get \(\$1\). If they get their chosen number on the second throw, they get \(\$2\). The same goes for the first time seeing their chosen number from throws \(3\) through \(6\). If they never get the chosen number, they have to pay \(\$1\).

What is the expected value and variance of a player playing this game?

Solution

Let \(X\) represent the winnings of a play of this game. We know that \(X\) takes a value in \(\{-1, 1, 2, 3, 4, 5, 6\}\). The \(p_X(-1)\) is given by the probability that the die never shows the chosen number. We can view this as \(6\) independent trials, where each trial is the result of a die roll. If \(A_j\) is the event that the die shows the selected number, then we can calculate \(P(A_1^C, A_2^C, A_3^C, A_4^C, A_5^C, A_6^C) = P(A_1^C)P(A_2^C)P(A_3^C)P(A_4^C)P(A_5^C)P(A_6^C)\). Note that each of these probabilities is equivalent, and equivalently equal to \(\dfrac{5}{6}\), and so this probability is \(\left(\dfrac{5}{6}\right)^6 \approx 0.335\). The remainder of the outcomes happen if the first time that the number shows up is on toss \(j\). This means that we have \(A_1, \dots, A_{j-1}^C\) and then \(A_j\) occurring. As a result, for \(j=1,\dots,6\) we get \(P(A_1^C, \dots, A_{j-1}^C, A_j) = P(A_1^C)^{j-1}P(A_j)\). Note that \(P(A_j) = \dfrac{1}{6}\), no matter \(j\), and so the total probability here is \(\left(\dfrac{5}{6}\right)^{j-1}\left(\dfrac{1}{6}\right)\). This fully defines the probability mass function.

To get the \(E[X]\) we can apply the standard expectation formula. To get the variance we can note that \(\text{var}(X) = E[X^2] - E[X]^2\), and so while we compute \(E[X]\) we can also compute \(E[X^2]\). To this end \[E[X] = (-1)\left(\frac{5}{5}\right)^6 + \frac{1}{6}\left[1 + 2\left(\frac{5}{6}\right) + 3\left(\frac{5}{6}\right)^{2} + 4\left(\frac{5}{6}\right)^{3} + 5\left(\frac{5}{6}\right)^{4}+ 6\left(\frac{5}{6}\right)^{5}\right].\] Solving this gives approximately \(\$0.98\), so every play of the game you would expect to earn \(98\) cents, approximately. To find \(E[X^2]\), we use essentially the same setup, this time squaring the values, \[E[X] = (-1)^2\left(\frac{5}{5}\right)^6 + \frac{1}{6}\left[1^2 + 2^2\left(\frac{5}{6}\right) + 3^2\left(\frac{5}{6}\right)^{2} + 4^2\left(\frac{5}{6}\right)^{3} + 5^2\left(\frac{5}{6}\right)^{4}+ 6^2\left(\frac{5}{6}\right)^{5}\right].\] This is \(8.728\), approximately. Then the variance will be given by \[\text{var}(X) = E[X^2] - E[X]^2 \approx 8.728 - (0.98)^2 = 7.7676.\]

6.7 The Variance of Transformations

With expectations, we saw that \(E[g(X)]\) needed to be directly computed from the definition. The same is true for variances of transformations. Specifically, \(\text{var}(g(X))\) is given by \(E[(g(X) - E[g(X)])^2]\) which can be simplified with the previous relationship as \(E[g(X)^2] - E[g(X)]^2\). Just as with expectations, it is important to realize that \(\text{var}(g(X)) \neq g(\text{var}(X))\), and so dealing with transformations requires further work.

With expectations, we highlighted linear transformations as a special case, with \(g(X) = aX + b\). For the variance, the linear transformations are also worth distinguishing from others. In particular, \[\text{var}(aX + b) = a^2\text{var}(X).\] In the same way that the linearity of expectation demonstrates that the expected value of any constant is that constant, we can use this identity to show that the variance of constant is zero. However, we can also reason to this based on our definitions so far. Suppose that we have a random variable which is constant.¹⁵ A constant \(b\) can be seen as a random variable with probability distribution \(p_X(x) = 1\) if \(x=b\) and \(p_X(x) = 0\) otherwise. The expected value is going to be \(E[X] = 1(b) = b\), and \(E[X^2] = 1(b)^2 = b^2\). Thus, \(\text{var}(b) = E[X^2] - E[X]^2 = b^2 - b^2 = 0\). From an intuitive perspective, there is no variation around the mean of a constant. It is always the same value. As a result, when taking the variance, we know that it should be \(0\).

Proof of the Variance of Linear Transformations

To calculate the variance of a linear transformation of a random variable we can apply the standard identity for the variance, giving \[\begin{align*} E[(aX+b)^2] &= E[a^2X^2 + 2abX + b^2] \\ &= E[a^2X^2] + E[2abX] + E[b^2]\\ &= a^2E[X^2] + 2abE[X] + b^2. \end{align*}\] Next, we note that \(E[aX + b] = aE[X] + b\) and so \[\begin{align*} E[aX + b]^2 &= (aE[X] + b)^2 \\ &= a^2E[X]^2 + 2abE[X] + b^2.\end{align*}\] Differencing these two quantities gives \[a^2E[X^2] + 2abE[X] + b^2 - a^2E[X]^2 - 2abE[X] - b^2 = a^2(E[X^2] - E[X]^2).\] By noting that \(E[X^2] - E[X]^2\), we can complete the statement that \[\text{var}(aX + b) = a^2\text{var}(X).\]

Thus, when applying a linear transformation, only the multiplicative constant matters, and it transforms the variance by a squared factor. This should make some intuitive sense that the additive constant does not change anything. If we consider that variance is a measure of spread, adding a constant value to our random quantity will not make it more or less spread out, it will simply shift where the spread is located. This is not true of the mean, which measures where the center of the distribution is, which helps explain why the result identities are different.

Example 6.17 (Sadie’s Trip to America) When Sadie had recently returned from a long trip to America, Charles and Sadie worked out how to convert the expected values of temperatures from Celsius to Fahrenheit. They now wish to do the same, with the variances. The distribution of daily temperatures, in Celsius, is \[p_X(x) = \begin{cases} 0.1 & x \in \{10, 11, 12, 13, 14\} \\ 0.05 & x \in \{15, 16, 17, 18, 19, 20, 21, 22, 23, 24\} \\ 0 & \text{otherwise} \end{cases}\]

1. What is the variance of temperatures, in Celsius?
2. Supposing that the temperature in Fahrenheit is given by \(Y = 1.8X + 32\), what is the variance of temperatures in Fahrenheit?

Solution

1. Here we find \[\begin{align*} E[X] = \sum_{x=10}^{24} xp_X(x) &= 0.1\sum_{x=10}^{14}x + 0.05\sum_{x=15}^{24}x \\ &= 15.75. \\ E[X^2] = \sum_{x=10}^{24} x^2p_X(x) &= 0.1\sum_{x=10}^{14}x^2 + 0.05\sum_{x=15}^{24}x^2 \\ &= 267.25 \\ \text{var}(X) &= 267.25 - 15.75^2 \\ &= 19.1875. \end{align*}\]

2. Since \(\text{var}(X) = 19.1875\), then we know that \(\text{var}(Y) = \text{var}(1.8X + 32) = 1.8^2\text{var}(X) = 62.1675\).

Unlike the expectation, the variance of additive terms will not generally be the addition of the variances themselves. That is, we cannot say that \(\text{var}(g(X) + h(X)) = \text{var}(g(X)) + \text{var}(h(X))\). Writing out the definition shows issue with this, \[E[(g(X) + h(X))^2] = E[g(X)^2] + 2E[g(X)h(X)] + E[h(X)^2].\] The first and third terms here are nicely separated and behave well. However, the central term is not generally easy to simplify. You can view \(g(X)h(X)\) as a function itself, and so \[E[g(X)h(X)] \neq E[g(X)]E[h(X)].\] Instead, this will typically need to be worked out for any specific set of functions.

Self-Assessment

Note: the following questions are still experimental. Please contact me if you have any issues with these components. This can be if there are incorrect answers, or if there are any technical concerns. Each question currently has an ID with it, randomized for each version. If you have issues, reporting the specific ID will allow for easier checking!

For each question, you can check your answer using the checkmark button. You can cycle through variants of the question by pressing the arrow icon.

Self Assessment 6.1

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $250,000.00 with probability 0.099.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $43025. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $43025?

Question ID: 0354930767

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $50.00 with probability 0.123, and a prize of $5,000.00 with probability 0.031.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $129. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $129?

Question ID: 0164246907

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $5,000.00 with probability 0.066, and a prize of $250,000.00 with probability 0.047.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $16793. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $16793?

Question ID: 0870013095

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $50,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $12782. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $12782?

Question ID: 0030580179

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $50,000.00 with probability 0.066.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $5228. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $5228?

Question ID: 0005899163

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $100.00 with probability 0.101, and a prize of $1,000,000.00 with probability 0.042.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $42010.47. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $42010.47?

Question ID: 0870483617

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $2,500.00 with probability 0.15, and a prize of $100,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $10518. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $10518?

Question ID: 0463825580

A lottery is proposed that would pay players a prize of $5.00 with probability 0.109, a prize of $75.00 with probability 0.075, and a prize of $5,000.00 with probability 0.05.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $131. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $131?

Question ID: 0232227299

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $250.00 with probability 0.15, and a prize of $10,000.00 with probability 0.135.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1398.75. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1398.75?

Question ID: 0528674136

A lottery is proposed that would pay players a prize of $500.00 with probability 0.15, a prize of $25,000.00 with probability 0.074, and a prize of $1,000,000.00 with probability 0.074.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $49732. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $49732?

Question ID: 0390300895

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $50,000.00 with probability 0.04.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2127.50. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2127.50?

Question ID: 0335533933

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $250.00 with probability 0.15, and a prize of $7,500.00 with probability 0.025.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $167. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $167?

Question ID: 0421247229

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $75,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $11400.38. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $11400.38?

Question ID: 0249056070

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $7,500.00 with probability 0.126, and a prize of $25,000.00 with probability 0.104.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $5328. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $5328?

Question ID: 0208818328

A lottery is proposed that would pay players a prize of $2,500.00 with probability 0.15, a prize of $75,000.00 with probability 0.109, and a prize of $750,000.00 with probability 0.043.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $40800.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $40800.00?

Question ID: 0996176265

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $50,000.00 with probability 0.109.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $4087. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $4087?

Question ID: 0641807344

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $100,000.00 with probability 0.15, and a prize of $500,000.00 with probability 0.063.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $65555. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $65555?

Question ID: 0119028232

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $1,000,000.00 with probability 0.002.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2871. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2871?

Question ID: 0198458666

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $75,000.00 with probability 0.111, and a prize of $500,000.00 with probability 0.015.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $11070. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $11070?

Question ID: 0146291302

A lottery is proposed that would pay players a prize of $750.00 with probability 0.15, a prize of $10,000.00 with probability 0.115, and a prize of $750,000.00 with probability 0.002.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1543. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1543?

Question ID: 0223369187

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $75,000.00 with probability 0.003.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $375.75. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $375.75?

Question ID: 0927585691

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $50,000.00 with probability 0.139.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $3620. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $3620?

Question ID: 0616538130

A lottery is proposed that would pay players a prize of $750.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $50,000.00 with probability 0.028.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2637.50. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2637.50?

Question ID: 0965998615

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $25.00 with probability 0.101, and a prize of $1,000.00 with probability 0.098.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $154. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $154?

Question ID: 0469527961

A lottery is proposed that would pay players a prize of $250.00 with probability 0.15, a prize of $100,000.00 with probability 0.15, and a prize of $750,000.00 with probability 0.092.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $78191. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $78191?

Question ID: 0045047766

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $500,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $110581. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $110581?

Question ID: 0874274371

A lottery is proposed that would pay players a prize of $25.00 with probability 0.15, a prize of $1,000.00 with probability 0.13, and a prize of $250,000.00 with probability 0.074.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $10973. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $10973?

Question ID: 0302513326

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $500.00 with probability 0.111, and a prize of $100,000.00 with probability 0.078.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $11882. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $11882?

Question ID: 0520931736

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $500.00 with probability 0.15, and a prize of $250,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $37575.38. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $37575.38?

Question ID: 0779467644

A lottery is proposed that would pay players a prize of $5.00 with probability 0.137, a prize of $2,500.00 with probability 0.067, and a prize of $1,000,000.00 with probability 0.012.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $13373. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $13373?

Question ID: 0009096298

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $5,000.00 with probability 0.15, and a prize of $50,000.00 with probability 0.093.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $4483. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $4483?

Question ID: 0283863949

A lottery is proposed that would pay players a prize of $1,000.00 with probability 0.15, a prize of $25,000.00 with probability 0.056, and a prize of $1,000,000.00 with probability 0.013.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $23382. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $23382?

Question ID: 0272346292

A lottery is proposed that would pay players a prize of $1,000.00 with probability 0.15, a prize of $100,000.00 with probability 0.093, and a prize of $250,000.00 with probability 0.01.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $15857. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $15857?

Question ID: 0617754335

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $75,000.00 with probability 0.079.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $6045.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $6045.00?

Question ID: 0529242171

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $50.00 with probability 0.15, and a prize of $50,000.00 with probability 0.083.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2965. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2965?

Question ID: 0299464345

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $250.00 with probability 0.15, and a prize of $50,000.00 with probability 0.035.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1789.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1789.00?

Question ID: 0088140347

A lottery is proposed that would pay players a prize of $1,000.00 with probability 0.15, a prize of $25,000.00 with probability 0.135, and a prize of $250,000.00 with probability 0.129.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $35775.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $35775.00?

Question ID: 0441143437

A lottery is proposed that would pay players a prize of $1,000.00 with probability 0.15, a prize of $25,000.00 with probability 0.134, and a prize of $750,000.00 with probability 0.102.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $55873. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $55873?

Question ID: 0476946209

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $1,000.00 with probability 0.108, and a prize of $10,000.00 with probability 0.019.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $313.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $313.00?

Question ID: 0494268482

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $100.00 with probability 0.15, and a prize of $750,000.00 with probability 0.063.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $47266.50. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $47266.50?

Question ID: 0768452451

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $25,000.00 with probability 0.15, and a prize of $1,000,000.00 with probability 0.039.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $30981. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $30981?

Question ID: 0730322196

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $50,000.00 with probability 0.11, and a prize of $750,000.00 with probability 0.067.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $55751.12. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $55751.12?

Question ID: 0957176680

A lottery is proposed that would pay players a prize of $5.00 with probability 0.092, a prize of $750.00 with probability 0.052, and a prize of $25,000.00 with probability 0.009.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $178. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $178?

Question ID: 0095449880

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $750.00 with probability 0.126, and a prize of $75,000.00 with probability 0.027.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2482. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2482?

Question ID: 0326564358

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $500.00 with probability 0.15, and a prize of $2,500.00 with probability 0.069.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $216. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $216?

Question ID: 0766685799

A lottery is proposed that would pay players a prize of $7.50 with probability 0.058, a prize of $1,000.00 with probability 0.039, and a prize of $250,000.00 with probability 0.013.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $2501. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $2501?

Question ID: 0697266853

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $250,000.00 with probability 0.093.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $23695. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $23695?

Question ID: 0200912290

A lottery is proposed that would pay players a prize of $500.00 with probability 0.15, a prize of $10,000.00 with probability 0.15, and a prize of $750,000.00 with probability 0.035.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $27825.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $27825.00?

Question ID: 0927966915

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $25.00 with probability 0.093, and a prize of $250,000.00 with probability 0.058.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $14502.70. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $14502.70?

Question ID: 0165761113

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $750.00 with probability 0.047, and a prize of $1,000,000.00 with probability 0.033.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $33042.75. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $33042.75?

Question ID: 0878145145

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $10,000.00 with probability 0.056.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $571.625. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $571.625?

Question ID: 0647154713

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $2,500.00 with probability 0.082, and a prize of $1,000,000.00 with probability 0.07.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $48878. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $48878?

Question ID: 0833769499

A lottery is proposed that would pay players a prize of $250.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $250,000.00 with probability 0.012.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $4162.50. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $4162.50?

Question ID: 0084044528

A lottery is proposed that would pay players a prize of $7,500.00 with probability 0.15, a prize of $25,000.00 with probability 0.15, and a prize of $250,000.00 with probability 0.097.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $46676. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $46676?

Question ID: 0405566463

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $50,000.00 with probability 0.15, and a prize of $500,000.00 with probability 0.103.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $31569. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $31569?

Question ID: 0271785822

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $500.00 with probability 0.141, and a prize of $2,500.00 with probability 0.128.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $767. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $767?

Question ID: 0629411982

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $10,000.00 with probability 0.102.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1752. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1752?

Question ID: 0168145057

A lottery is proposed that would pay players a prize of $750.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $750,000.00 with probability 0.033.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $41835. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $41835?

Question ID: 0821774898

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $5,000.00 with probability 0.15, and a prize of $75,000.00 with probability 0.114.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $5295. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $5295?

Question ID: 0847457667

A lottery is proposed that would pay players a prize of $7.50 with probability 0.072, a prize of $25.00 with probability 0.005, and a prize of $1,000,000.00 with probability 0.002.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1570. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1570?

Question ID: 0523018823

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $75.00 with probability 0.087, and a prize of $1,000,000.00 with probability 0.05.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $50007.27. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $50007.27?

Question ID: 0035897931

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $2,500.00 with probability 0.15, and a prize of $500,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $75382.50. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $75382.50?

Question ID: 0475741159

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $100.00 with probability 0.106, and a prize of $500,000.00 with probability 0.012.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $3218. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $3218?

Question ID: 0616647839

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $500.00 with probability 0.117, and a prize of $50,000.00 with probability 0.025.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $767. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $767?

Question ID: 0515170992

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $250.00 with probability 0.1, and a prize of $75,000.00 with probability 0.052.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $3551. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $3551?

Question ID: 0858359376

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $10,000.00 with probability 0.022, and a prize of $100,000.00 with probability 0.006.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1157. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1157?

Question ID: 0421259096

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $25,000.00 with probability 0.15, and a prize of $1,000,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $284616. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $284616?

Question ID: 0791462786

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $50.00 with probability 0.115, and a prize of $5,000.00 with probability 0.001.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $9. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $9?

Question ID: 0023668264

A lottery is proposed that would pay players a prize of $50.00 with probability 0.148, a prize of $250.00 with probability 0.139, and a prize of $750,000.00 with probability 0.112.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $84042.15. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $84042.15?

Question ID: 0119867126

A lottery is proposed that would pay players a prize of $25.00 with probability 0.15, a prize of $250.00 with probability 0.15, and a prize of $100,000.00 with probability 0.099.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $12593. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $12593?

Question ID: 0091934752

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $25.00 with probability 0.15, and a prize of $25,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $6694. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $6694?

Question ID: 0528297641

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $100.00 with probability 0.134, and a prize of $750,000.00 with probability 0.012.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $9014.525. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $9014.525?

Question ID: 0267317843

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $7,500.00 with probability 0.089, and a prize of $750,000.00 with probability 0.008.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $6675.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $6675.00?

Question ID: 0019876677

A lottery is proposed that would pay players a prize of $500.00 with probability 0.15, a prize of $5,000.00 with probability 0.116, and a prize of $1,000,000.00 with probability 0.083.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $83655.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $83655.00?

Question ID: 0115054122

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $10,000.00 with probability 0.118, and a prize of $25,000.00 with probability 0.073.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $3314. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $3314?

Question ID: 0324363628

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $75,000.00 with probability 0.15, and a prize of $500,000.00 with probability 0.035.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $53590. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $53590?

Question ID: 0642870191

A lottery is proposed that would pay players a prize of $750.00 with probability 0.076, a prize of $7,500.00 with probability 0.048, and a prize of $1,000,000.00 with probability 0.025.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $26819. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $26819?

Question ID: 0394185287

A lottery is proposed that would pay players a prize of $2,500.00 with probability 0.15, a prize of $50,000.00 with probability 0.073, and a prize of $500,000.00 with probability 0.029.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $18525.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $18525.00?

Question ID: 0881478041

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $750.00 with probability 0.114, and a prize of $7,500.00 with probability 0.096.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $805.875. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $805.875?

Question ID: 0355487680

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $2,500.00 with probability 0.15, and a prize of $75,000.00 with probability 0.011.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1372. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1372?

Question ID: 0612936733

A lottery is proposed that would pay players a prize of $500.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $1,000,000.00 with probability 0.035.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $36200.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $36200.00?

Question ID: 0802902833

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $75,000.00 with probability 0.067.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $4913. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $4913?

Question ID: 0592908242

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $5,000.00 with probability 0.044.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $614. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $614?

Question ID: 0268244531

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $100,000.00 with probability 0.15, and a prize of $250,000.00 with probability 0.004.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $12440. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $12440?

Question ID: 0733456738

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $250.00 with probability 0.15, and a prize of $5,000.00 with probability 0.15.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $653. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $653?

Question ID: 0084940653

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $1,000,000.00 with probability 0.076.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $76150.37. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $76150.37?

Question ID: 0393841277

A lottery is proposed that would pay players a prize of $10.00 with probability 0.123, a prize of $750.00 with probability 0.102, and a prize of $750,000.00 with probability 0.024.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $18077.73. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $18077.73?

Question ID: 0196250009

A lottery is proposed that would pay players a prize of $500.00 with probability 0.15, a prize of $100,000.00 with probability 0.099, and a prize of $750,000.00 with probability 0.014.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $21977. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $21977?

Question ID: 0951700812

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $25,000.00 with probability 0.15, and a prize of $750,000.00 with probability 0.022.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $20989. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $20989?

Question ID: 0099019967

A lottery is proposed that would pay players a prize of $25.00 with probability 0.15, a prize of $7,500.00 with probability 0.15, and a prize of $25,000.00 with probability 0.002.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $1169. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $1169?

Question ID: 0260738443

A lottery is proposed that would pay players a prize of $2.50 with probability 0.15, a prize of $250.00 with probability 0.077, and a prize of $1,000,000.00 with probability 0.023.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $15253. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $15253?

Question ID: 0491497146

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $10,000.00 with probability 0.132, and a prize of $500,000.00 with probability 0.058.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $16731. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $16731?

Question ID: 0035179936

A lottery is proposed that would pay players a prize of $10.00 with probability 0.15, a prize of $1,000.00 with probability 0.15, and a prize of $2,500.00 with probability 0.109.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $424.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $424.00?

Question ID: 0168960453

A lottery is proposed that would pay players a prize of $25.00 with probability 0.15, a prize of $500.00 with probability 0.099, and a prize of $2,500.00 with probability 0.036.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $137. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $137?

Question ID: 0358215279

A lottery is proposed that would pay players a prize of $100.00 with probability 0.15, a prize of $25,000.00 with probability 0.13, and a prize of $1,000,000.00 with probability 0.03.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $33265.00. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $33265.00?

Question ID: 0395978203

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $75.00 with probability 0.15, and a prize of $7,500.00 with probability 0.029.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $443. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $443?

Question ID: 0872045136

A lottery is proposed that would pay players a prize of $5.00 with probability 0.15, a prize of $75.00 with probability 0.093, and a prize of $5,000.00 with probability 0.068.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $347.725. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $347.725?

Question ID: 0366703909

A lottery is proposed that would pay players a prize of $7.50 with probability 0.15, a prize of $750.00 with probability 0.15, and a prize of $5,000.00 with probability 0.003.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $76. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $76?

Question ID: 0334792066

A lottery is proposed that would pay players a prize of $75.00 with probability 0.15, a prize of $5,000.00 with probability 0.15, and a prize of $100,000.00 with probability 0.029.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $6648. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $6648?

Question ID: 0885334318

A lottery is proposed that would pay players a prize of $50.00 with probability 0.15, a prize of $5,000.00 with probability 0.138, and a prize of $500,000.00 with probability 0.04.

1. If the game is to be fair, how much should it cost to play this lottery?
2. Suppose that a ticket of playing this lottery costs $14424. What is the expected value of a single lottery ticket?
3. What is the variance of the payout from a single lottery ticket?
4. What is the standard deviation of the total earnings from a single lottery ticket, if it costs $14424?

Question ID: 0713805422

Self Assessment 6.2

Suppose that \(X\) is a random variable with \(E[X] = -1\) and \(\text{var}(X) = 30\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-43X + 29]\)?
2. What is \(\text{var}(-43X + 29)\)?
3. What is \(E[-43X^2 + 29]\)?

Question ID: 0389838355

Suppose that \(X\) is a random variable with \(E[X] = -10\) and \(\text{var}(X) = 83\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-44X - 11]\)?
2. What is \(\text{var}(-44X - 11)\)?
3. What is \(E[-44X^2 - 11]\)?

Question ID: 0875945982

Suppose that \(X\) is a random variable with \(E[X] = 23\) and \(\text{var}(X) = 11\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[35X - 21]\)?
2. What is \(\text{var}(35X - 21)\)?
3. What is \(E[35X^2 - 21]\)?

Question ID: 0321009316

Suppose that \(X\) is a random variable with \(E[X] = 49\) and \(\text{var}(X) = 52\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[47X - 4]\)?
2. What is \(\text{var}(47X - 4)\)?
3. What is \(E[47X^2 - 4]\)?

Question ID: 0349560366

Suppose that \(X\) is a random variable with \(E[X] = 11\) and \(\text{var}(X) = 62\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-32X + 21]\)?
2. What is \(\text{var}(-32X + 21)\)?
3. What is \(E[-32X^2 + 21]\)?

Question ID: 0747818635

Suppose that \(X\) is a random variable with \(E[X] = -3\) and \(\text{var}(X) = 78\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[24X - 10]\)?
2. What is \(\text{var}(24X - 10)\)?
3. What is \(E[24X^2 - 10]\)?

Question ID: 0438882725

Suppose that \(X\) is a random variable with \(E[X] = -48\) and \(\text{var}(X) = 44\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-48X + 37]\)?
2. What is \(\text{var}(-48X + 37)\)?
3. What is \(E[-48X^2 + 37]\)?

Question ID: 0455333783

Suppose that \(X\) is a random variable with \(E[X] = 29\) and \(\text{var}(X) = 71\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-6X + 45]\)?
2. What is \(\text{var}(-6X + 45)\)?
3. What is \(E[-6X^2 + 45]\)?

Question ID: 0795600888

Suppose that \(X\) is a random variable with \(E[X] = 30\) and \(\text{var}(X) = 6\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[33X + 43]\)?
2. What is \(\text{var}(33X + 43)\)?
3. What is \(E[33X^2 + 43]\)?

Question ID: 0815189565

Suppose that \(X\) is a random variable with \(E[X] = -14\) and \(\text{var}(X) = 86\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[42X - 36]\)?
2. What is \(\text{var}(42X - 36)\)?
3. What is \(E[42X^2 - 36]\)?

Question ID: 0092652688

Suppose that \(X\) is a random variable with \(E[X] = 47\) and \(\text{var}(X) = 92\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[43X + 25]\)?
2. What is \(\text{var}(43X + 25)\)?
3. What is \(E[43X^2 + 25]\)?

Question ID: 0406822221

Suppose that \(X\) is a random variable with \(E[X] = -42\) and \(\text{var}(X) = 87\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-12X + 26]\)?
2. What is \(\text{var}(-12X + 26)\)?
3. What is \(E[-12X^2 + 26]\)?

Question ID: 0203899783

Suppose that \(X\) is a random variable with \(E[X] = -35\) and \(\text{var}(X) = 33\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[40X - 29]\)?
2. What is \(\text{var}(40X - 29)\)?
3. What is \(E[40X^2 - 29]\)?

Question ID: 0805171559

Suppose that \(X\) is a random variable with \(E[X] = 45\) and \(\text{var}(X) = 43\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-16X + 6]\)?
2. What is \(\text{var}(-16X + 6)\)?
3. What is \(E[-16X^2 + 6]\)?

Question ID: 0363739129

Suppose that \(X\) is a random variable with \(E[X] = -49\) and \(\text{var}(X) = 66\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-38X - 30]\)?
2. What is \(\text{var}(-38X - 30)\)?
3. What is \(E[-38X^2 - 30]\)?

Question ID: 0436683332

Suppose that \(X\) is a random variable with \(E[X] = 18\) and \(\text{var}(X) = 30\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[22X + 24]\)?
2. What is \(\text{var}(22X + 24)\)?
3. What is \(E[22X^2 + 24]\)?

Question ID: 0921784945

Suppose that \(X\) is a random variable with \(E[X] = 19\) and \(\text{var}(X) = 86\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[43X - 12]\)?
2. What is \(\text{var}(43X - 12)\)?
3. What is \(E[43X^2 - 12]\)?

Question ID: 0664291534

Suppose that \(X\) is a random variable with \(E[X] = 15\) and \(\text{var}(X) = 25\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[1X - 6]\)?
2. What is \(\text{var}(1X - 6)\)?
3. What is \(E[1X^2 - 6]\)?

Question ID: 0157320951

Suppose that \(X\) is a random variable with \(E[X] = 15\) and \(\text{var}(X) = 73\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-29X + 49]\)?
2. What is \(\text{var}(-29X + 49)\)?
3. What is \(E[-29X^2 + 49]\)?

Question ID: 0334994678

Suppose that \(X\) is a random variable with \(E[X] = -5\) and \(\text{var}(X) = 82\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-38X - 43]\)?
2. What is \(\text{var}(-38X - 43)\)?
3. What is \(E[-38X^2 - 43]\)?

Question ID: 0386256330

Suppose that \(X\) is a random variable with \(E[X] = -10\) and \(\text{var}(X) = 24\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[6X - 21]\)?
2. What is \(\text{var}(6X - 21)\)?
3. What is \(E[6X^2 - 21]\)?

Question ID: 0874848876

Suppose that \(X\) is a random variable with \(E[X] = 30\) and \(\text{var}(X) = 5\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[32X - 28]\)?
2. What is \(\text{var}(32X - 28)\)?
3. What is \(E[32X^2 - 28]\)?

Question ID: 0918460167

Suppose that \(X\) is a random variable with \(E[X] = -46\) and \(\text{var}(X) = 50\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-8X - 48]\)?
2. What is \(\text{var}(-8X - 48)\)?
3. What is \(E[-8X^2 - 48]\)?

Question ID: 0654163188

Suppose that \(X\) is a random variable with \(E[X] = 43\) and \(\text{var}(X) = 23\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-31X - 47]\)?
2. What is \(\text{var}(-31X - 47)\)?
3. What is \(E[-31X^2 - 47]\)?

Question ID: 0735235852

Suppose that \(X\) is a random variable with \(E[X] = -31\) and \(\text{var}(X) = 92\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[2X - 14]\)?
2. What is \(\text{var}(2X - 14)\)?
3. What is \(E[2X^2 - 14]\)?

Question ID: 0847283418

Suppose that \(X\) is a random variable with \(E[X] = 38\) and \(\text{var}(X) = 46\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[28X + 34]\)?
2. What is \(\text{var}(28X + 34)\)?
3. What is \(E[28X^2 + 34]\)?

Question ID: 0452734355

Suppose that \(X\) is a random variable with \(E[X] = -43\) and \(\text{var}(X) = 77\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[22X - 35]\)?
2. What is \(\text{var}(22X - 35)\)?
3. What is \(E[22X^2 - 35]\)?

Question ID: 0555396165

Suppose that \(X\) is a random variable with \(E[X] = -47\) and \(\text{var}(X) = 10\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-40X + 6]\)?
2. What is \(\text{var}(-40X + 6)\)?
3. What is \(E[-40X^2 + 6]\)?

Question ID: 0356064475

Suppose that \(X\) is a random variable with \(E[X] = 22\) and \(\text{var}(X) = 97\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-30X - 2]\)?
2. What is \(\text{var}(-30X - 2)\)?
3. What is \(E[-30X^2 - 2]\)?

Question ID: 0030679819

Suppose that \(X\) is a random variable with \(E[X] = -15\) and \(\text{var}(X) = 92\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[42X - 7]\)?
2. What is \(\text{var}(42X - 7)\)?
3. What is \(E[42X^2 - 7]\)?

Question ID: 0830789004

Suppose that \(X\) is a random variable with \(E[X] = 46\) and \(\text{var}(X) = 45\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[49X - 38]\)?
2. What is \(\text{var}(49X - 38)\)?
3. What is \(E[49X^2 - 38]\)?

Question ID: 0531995435

Suppose that \(X\) is a random variable with \(E[X] = 50\) and \(\text{var}(X) = 62\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-48X - 35]\)?
2. What is \(\text{var}(-48X - 35)\)?
3. What is \(E[-48X^2 - 35]\)?

Question ID: 0213138200

Suppose that \(X\) is a random variable with \(E[X] = 50\) and \(\text{var}(X) = 21\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[39X - 32]\)?
2. What is \(\text{var}(39X - 32)\)?
3. What is \(E[39X^2 - 32]\)?

Question ID: 0359506659

Suppose that \(X\) is a random variable with \(E[X] = -1\) and \(\text{var}(X) = 52\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-7X - 30]\)?
2. What is \(\text{var}(-7X - 30)\)?
3. What is \(E[-7X^2 - 30]\)?

Question ID: 0755796523

Suppose that \(X\) is a random variable with \(E[X] = -16\) and \(\text{var}(X) = 73\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-2X + 43]\)?
2. What is \(\text{var}(-2X + 43)\)?
3. What is \(E[-2X^2 + 43]\)?

Question ID: 0072324677

Suppose that \(X\) is a random variable with \(E[X] = 27\) and \(\text{var}(X) = 11\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-48X - 30]\)?
2. What is \(\text{var}(-48X - 30)\)?
3. What is \(E[-48X^2 - 30]\)?

Question ID: 0116553218

Suppose that \(X\) is a random variable with \(E[X] = 27\) and \(\text{var}(X) = 58\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-11X - 33]\)?
2. What is \(\text{var}(-11X - 33)\)?
3. What is \(E[-11X^2 - 33]\)?

Question ID: 0546088900

Suppose that \(X\) is a random variable with \(E[X] = 3\) and \(\text{var}(X) = 64\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[46X - 39]\)?
2. What is \(\text{var}(46X - 39)\)?
3. What is \(E[46X^2 - 39]\)?

Question ID: 0974255443

Suppose that \(X\) is a random variable with \(E[X] = -1\) and \(\text{var}(X) = 99\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[18X + 43]\)?
2. What is \(\text{var}(18X + 43)\)?
3. What is \(E[18X^2 + 43]\)?

Question ID: 0753829012

Suppose that \(X\) is a random variable with \(E[X] = 25\) and \(\text{var}(X) = 41\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-21X + 23]\)?
2. What is \(\text{var}(-21X + 23)\)?
3. What is \(E[-21X^2 + 23]\)?

Question ID: 0896550678

Suppose that \(X\) is a random variable with \(E[X] = -48\) and \(\text{var}(X) = 17\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[45X - 12]\)?
2. What is \(\text{var}(45X - 12)\)?
3. What is \(E[45X^2 - 12]\)?

Question ID: 0882380301

Suppose that \(X\) is a random variable with \(E[X] = 4\) and \(\text{var}(X) = 38\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[12X + 38]\)?
2. What is \(\text{var}(12X + 38)\)?
3. What is \(E[12X^2 + 38]\)?

Question ID: 0486723718

Suppose that \(X\) is a random variable with \(E[X] = 22\) and \(\text{var}(X) = 41\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[42X + 34]\)?
2. What is \(\text{var}(42X + 34)\)?
3. What is \(E[42X^2 + 34]\)?

Question ID: 0828038002

Suppose that \(X\) is a random variable with \(E[X] = 9\) and \(\text{var}(X) = 54\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[38X - 18]\)?
2. What is \(\text{var}(38X - 18)\)?
3. What is \(E[38X^2 - 18]\)?

Question ID: 0044772212

Suppose that \(X\) is a random variable with \(E[X] = -33\) and \(\text{var}(X) = 90\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[21X - 44]\)?
2. What is \(\text{var}(21X - 44)\)?
3. What is \(E[21X^2 - 44]\)?

Question ID: 0958522030

Suppose that \(X\) is a random variable with \(E[X] = -21\) and \(\text{var}(X) = 4\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[36X + 31]\)?
2. What is \(\text{var}(36X + 31)\)?
3. What is \(E[36X^2 + 31]\)?

Question ID: 0066701059

Suppose that \(X\) is a random variable with \(E[X] = -47\) and \(\text{var}(X) = 87\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-4X - 22]\)?
2. What is \(\text{var}(-4X - 22)\)?
3. What is \(E[-4X^2 - 22]\)?

Question ID: 0482033972

Suppose that \(X\) is a random variable with \(E[X] = -14\) and \(\text{var}(X) = 55\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-15X + 28]\)?
2. What is \(\text{var}(-15X + 28)\)?
3. What is \(E[-15X^2 + 28]\)?

Question ID: 0208508328

Suppose that \(X\) is a random variable with \(E[X] = 48\) and \(\text{var}(X) = 20\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[30X + 17]\)?
2. What is \(\text{var}(30X + 17)\)?
3. What is \(E[30X^2 + 17]\)?

Question ID: 0914651672

Suppose that \(X\) is a random variable with \(E[X] = -41\) and \(\text{var}(X) = 23\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[45X - 11]\)?
2. What is \(\text{var}(45X - 11)\)?
3. What is \(E[45X^2 - 11]\)?

Question ID: 0366814186

Suppose that \(X\) is a random variable with \(E[X] = -31\) and \(\text{var}(X) = 11\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-44X - 47]\)?
2. What is \(\text{var}(-44X - 47)\)?
3. What is \(E[-44X^2 - 47]\)?

Question ID: 0009321237

Suppose that \(X\) is a random variable with \(E[X] = 47\) and \(\text{var}(X) = 87\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-31X - 26]\)?
2. What is \(\text{var}(-31X - 26)\)?
3. What is \(E[-31X^2 - 26]\)?

Question ID: 0118057641

Suppose that \(X\) is a random variable with \(E[X] = 8\) and \(\text{var}(X) = 64\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-6X + 32]\)?
2. What is \(\text{var}(-6X + 32)\)?
3. What is \(E[-6X^2 + 32]\)?

Question ID: 0670345296

Suppose that \(X\) is a random variable with \(E[X] = -9\) and \(\text{var}(X) = 81\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-36X + 3]\)?
2. What is \(\text{var}(-36X + 3)\)?
3. What is \(E[-36X^2 + 3]\)?

Question ID: 0285277554

Suppose that \(X\) is a random variable with \(E[X] = 8\) and \(\text{var}(X) = 18\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-31X - 23]\)?
2. What is \(\text{var}(-31X - 23)\)?
3. What is \(E[-31X^2 - 23]\)?

Question ID: 0099314524

Suppose that \(X\) is a random variable with \(E[X] = 7\) and \(\text{var}(X) = 87\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[2X + 21]\)?
2. What is \(\text{var}(2X + 21)\)?
3. What is \(E[2X^2 + 21]\)?

Question ID: 0847904369

Suppose that \(X\) is a random variable with \(E[X] = 26\) and \(\text{var}(X) = 14\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-49X + 5]\)?
2. What is \(\text{var}(-49X + 5)\)?
3. What is \(E[-49X^2 + 5]\)?

Question ID: 0756791907

Suppose that \(X\) is a random variable with \(E[X] = -36\) and \(\text{var}(X) = 31\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[23X + 33]\)?
2. What is \(\text{var}(23X + 33)\)?
3. What is \(E[23X^2 + 33]\)?

Question ID: 0131725087

Suppose that \(X\) is a random variable with \(E[X] = -32\) and \(\text{var}(X) = 62\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-36X - 41]\)?
2. What is \(\text{var}(-36X - 41)\)?
3. What is \(E[-36X^2 - 41]\)?

Question ID: 0285808066

Suppose that \(X\) is a random variable with \(E[X] = 12\) and \(\text{var}(X) = 19\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-43X - 13]\)?
2. What is \(\text{var}(-43X - 13)\)?
3. What is \(E[-43X^2 - 13]\)?

Question ID: 0456657457

Suppose that \(X\) is a random variable with \(E[X] = -30\) and \(\text{var}(X) = 97\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-25X - 28]\)?
2. What is \(\text{var}(-25X - 28)\)?
3. What is \(E[-25X^2 - 28]\)?

Question ID: 0350557819

Suppose that \(X\) is a random variable with \(E[X] = -36\) and \(\text{var}(X) = 4\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-26X - 24]\)?
2. What is \(\text{var}(-26X - 24)\)?
3. What is \(E[-26X^2 - 24]\)?

Question ID: 0911937900

Suppose that \(X\) is a random variable with \(E[X] = -9\) and \(\text{var}(X) = 9\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[13X + 45]\)?
2. What is \(\text{var}(13X + 45)\)?
3. What is \(E[13X^2 + 45]\)?

Question ID: 0263325860

Suppose that \(X\) is a random variable with \(E[X] = 34\) and \(\text{var}(X) = 14\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[2X + 41]\)?
2. What is \(\text{var}(2X + 41)\)?
3. What is \(E[2X^2 + 41]\)?

Question ID: 0709005897

Suppose that \(X\) is a random variable with \(E[X] = 31\) and \(\text{var}(X) = 100\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[17X + 34]\)?
2. What is \(\text{var}(17X + 34)\)?
3. What is \(E[17X^2 + 34]\)?

Question ID: 0189116110

Suppose that \(X\) is a random variable with \(E[X] = 2\) and \(\text{var}(X) = 93\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-20X + 45]\)?
2. What is \(\text{var}(-20X + 45)\)?
3. What is \(E[-20X^2 + 45]\)?

Question ID: 0649344515

Suppose that \(X\) is a random variable with \(E[X] = -31\) and \(\text{var}(X) = 39\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-22X - 6]\)?
2. What is \(\text{var}(-22X - 6)\)?
3. What is \(E[-22X^2 - 6]\)?

Question ID: 0583818678

Suppose that \(X\) is a random variable with \(E[X] = -25\) and \(\text{var}(X) = 68\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[28X - 17]\)?
2. What is \(\text{var}(28X - 17)\)?
3. What is \(E[28X^2 - 17]\)?

Question ID: 0673206981

Suppose that \(X\) is a random variable with \(E[X] = 43\) and \(\text{var}(X) = 100\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[45X - 5]\)?
2. What is \(\text{var}(45X - 5)\)?
3. What is \(E[45X^2 - 5]\)?

Question ID: 0735283530

Suppose that \(X\) is a random variable with \(E[X] = -32\) and \(\text{var}(X) = 71\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[34X - 43]\)?
2. What is \(\text{var}(34X - 43)\)?
3. What is \(E[34X^2 - 43]\)?

Question ID: 0845000919

Suppose that \(X\) is a random variable with \(E[X] = 12\) and \(\text{var}(X) = 44\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-29X - 40]\)?
2. What is \(\text{var}(-29X - 40)\)?
3. What is \(E[-29X^2 - 40]\)?

Question ID: 0298820385

Suppose that \(X\) is a random variable with \(E[X] = 37\) and \(\text{var}(X) = 41\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-31X - 32]\)?
2. What is \(\text{var}(-31X - 32)\)?
3. What is \(E[-31X^2 - 32]\)?

Question ID: 0212598401

Suppose that \(X\) is a random variable with \(E[X] = -29\) and \(\text{var}(X) = 58\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-33X - 26]\)?
2. What is \(\text{var}(-33X - 26)\)?
3. What is \(E[-33X^2 - 26]\)?

Question ID: 0788411664

Suppose that \(X\) is a random variable with \(E[X] = 7\) and \(\text{var}(X) = 14\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-19X - 13]\)?
2. What is \(\text{var}(-19X - 13)\)?
3. What is \(E[-19X^2 - 13]\)?

Question ID: 0849396502

Suppose that \(X\) is a random variable with \(E[X] = -28\) and \(\text{var}(X) = 92\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[10X + 1]\)?
2. What is \(\text{var}(10X + 1)\)?
3. What is \(E[10X^2 + 1]\)?

Question ID: 0468885968

Suppose that \(X\) is a random variable with \(E[X] = -27\) and \(\text{var}(X) = 17\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-2X - 17]\)?
2. What is \(\text{var}(-2X - 17)\)?
3. What is \(E[-2X^2 - 17]\)?

Question ID: 0491265405

Suppose that \(X\) is a random variable with \(E[X] = 7\) and \(\text{var}(X) = 40\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[15X - 31]\)?
2. What is \(\text{var}(15X - 31)\)?
3. What is \(E[15X^2 - 31]\)?

Question ID: 0782868506

Suppose that \(X\) is a random variable with \(E[X] = 32\) and \(\text{var}(X) = 6\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-8X + 3]\)?
2. What is \(\text{var}(-8X + 3)\)?
3. What is \(E[-8X^2 + 3]\)?

Question ID: 0690488738

Suppose that \(X\) is a random variable with \(E[X] = 11\) and \(\text{var}(X) = 4\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-5X + 11]\)?
2. What is \(\text{var}(-5X + 11)\)?
3. What is \(E[-5X^2 + 11]\)?

Question ID: 0904578193

Suppose that \(X\) is a random variable with \(E[X] = -2\) and \(\text{var}(X) = 76\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[37X + 4]\)?
2. What is \(\text{var}(37X + 4)\)?
3. What is \(E[37X^2 + 4]\)?

Question ID: 0148114025

Suppose that \(X\) is a random variable with \(E[X] = 17\) and \(\text{var}(X) = 71\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[12X - 25]\)?
2. What is \(\text{var}(12X - 25)\)?
3. What is \(E[12X^2 - 25]\)?

Question ID: 0863123095

Suppose that \(X\) is a random variable with \(E[X] = 25\) and \(\text{var}(X) = 87\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[40X - 9]\)?
2. What is \(\text{var}(40X - 9)\)?
3. What is \(E[40X^2 - 9]\)?

Question ID: 0955431271

Suppose that \(X\) is a random variable with \(E[X] = 38\) and \(\text{var}(X) = 89\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-12X - 11]\)?
2. What is \(\text{var}(-12X - 11)\)?
3. What is \(E[-12X^2 - 11]\)?

Question ID: 0211493452

Suppose that \(X\) is a random variable with \(E[X] = -49\) and \(\text{var}(X) = 57\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[29X - 30]\)?
2. What is \(\text{var}(29X - 30)\)?
3. What is \(E[29X^2 - 30]\)?

Question ID: 0940576052

Suppose that \(X\) is a random variable with \(E[X] = 5\) and \(\text{var}(X) = 30\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-6X - 46]\)?
2. What is \(\text{var}(-6X - 46)\)?
3. What is \(E[-6X^2 - 46]\)?

Question ID: 0383679914

Suppose that \(X\) is a random variable with \(E[X] = -32\) and \(\text{var}(X) = 67\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[30X + 32]\)?
2. What is \(\text{var}(30X + 32)\)?
3. What is \(E[30X^2 + 32]\)?

Question ID: 0171445125

Suppose that \(X\) is a random variable with \(E[X] = -12\) and \(\text{var}(X) = 24\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[6X + 32]\)?
2. What is \(\text{var}(6X + 32)\)?
3. What is \(E[6X^2 + 32]\)?

Question ID: 0224404908

Suppose that \(X\) is a random variable with \(E[X] = 46\) and \(\text{var}(X) = 1\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[38X + 13]\)?
2. What is \(\text{var}(38X + 13)\)?
3. What is \(E[38X^2 + 13]\)?

Question ID: 0272760163

Suppose that \(X\) is a random variable with \(E[X] = 7\) and \(\text{var}(X) = 69\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[7X + 1]\)?
2. What is \(\text{var}(7X + 1)\)?
3. What is \(E[7X^2 + 1]\)?

Question ID: 0292251086

Suppose that \(X\) is a random variable with \(E[X] = 14\) and \(\text{var}(X) = 76\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-8X - 7]\)?
2. What is \(\text{var}(-8X - 7)\)?
3. What is \(E[-8X^2 - 7]\)?

Question ID: 0305976544

Suppose that \(X\) is a random variable with \(E[X] = -17\) and \(\text{var}(X) = 51\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-23X + 48]\)?
2. What is \(\text{var}(-23X + 48)\)?
3. What is \(E[-23X^2 + 48]\)?

Question ID: 0241444019

Suppose that \(X\) is a random variable with \(E[X] = 2\) and \(\text{var}(X) = 27\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-17X + 14]\)?
2. What is \(\text{var}(-17X + 14)\)?
3. What is \(E[-17X^2 + 14]\)?

Question ID: 0297938845

Suppose that \(X\) is a random variable with \(E[X] = -1\) and \(\text{var}(X) = 84\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-14X - 1]\)?
2. What is \(\text{var}(-14X - 1)\)?
3. What is \(E[-14X^2 - 1]\)?

Question ID: 0904391662

Suppose that \(X\) is a random variable with \(E[X] = -50\) and \(\text{var}(X) = 48\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[32X - 6]\)?
2. What is \(\text{var}(32X - 6)\)?
3. What is \(E[32X^2 - 6]\)?

Question ID: 0983550987

Suppose that \(X\) is a random variable with \(E[X] = 45\) and \(\text{var}(X) = 44\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-44X - 45]\)?
2. What is \(\text{var}(-44X - 45)\)?
3. What is \(E[-44X^2 - 45]\)?

Question ID: 0489973271

Suppose that \(X\) is a random variable with \(E[X] = -10\) and \(\text{var}(X) = 85\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[7X - 47]\)?
2. What is \(\text{var}(7X - 47)\)?
3. What is \(E[7X^2 - 47]\)?

Question ID: 0619818842

Suppose that \(X\) is a random variable with \(E[X] = -29\) and \(\text{var}(X) = 95\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-42X + 30]\)?
2. What is \(\text{var}(-42X + 30)\)?
3. What is \(E[-42X^2 + 30]\)?

Question ID: 0108333402

Suppose that \(X\) is a random variable with \(E[X] = 40\) and \(\text{var}(X) = 36\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-16X + 20]\)?
2. What is \(\text{var}(-16X + 20)\)?
3. What is \(E[-16X^2 + 20]\)?

Question ID: 0290601258

Suppose that \(X\) is a random variable with \(E[X] = -4\) and \(\text{var}(X) = 60\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[-14X + 4]\)?
2. What is \(\text{var}(-14X + 4)\)?
3. What is \(E[-14X^2 + 4]\)?

Question ID: 0714426979

Suppose that \(X\) is a random variable with \(E[X] = 50\) and \(\text{var}(X) = 90\).

Answer the following questions. If ever you are not provided sufficient information, enter a value of -1.

1. What is \(E[36X + 38]\)?
2. What is \(\text{var}(36X + 38)\)?
3. What is \(E[36X^2 + 38]\)?

Question ID: 0914863436

Self Assessment 6.3

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.19 & x = 15\\0.31 & x = 34\\0.17 & x = 41\\0.12 & x = 45\\0.21 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 62th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0203482805

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.28 & x = 4\\0.24 & x = 10\\0.23 & x = 17\\0.11 & x = 34\\0.14 & x = 39\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 92th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0456486690

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.32 & x = 3\\0.1 & x = 5\\0.2 & x = 11\\0.29 & x = 33\\0.09 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 79th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0823544268

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.1 & x = 0\\0.06 & x = 3\\0.23 & x = 7\\0.47 & x = 29\\0.14 & x = 37\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 26th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0288307729

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.21 & x = 16\\0.07 & x = 21\\0.05 & x = 33\\0 & x = 40\\0.67 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 68th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0605220038

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 10\\0.28 & x = 15\\0.25 & x = 24\\0.1 & x = 35\\0.3 & x = 39\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 74th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0878410977

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 2\\0.22 & x = 6\\0.43 & x = 8\\0.26 & x = 9\\0.01 & x = 18\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 63th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0645927823

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 13\\0.13 & x = 30\\0.4 & x = 32\\0.22 & x = 37\\0.18 & x = 45\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 17th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0190008803

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.25 & x = 7\\0.2 & x = 9\\0.47 & x = 27\\0.05 & x = 36\\0.03 & x = 41\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 55th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0709229751

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.19 & x = 16\\0.15 & x = 19\\0.1 & x = 21\\0.42 & x = 44\\0.14 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 70th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0499170570

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.22 & x = 12\\0.28 & x = 14\\0.31 & x = 16\\0 & x = 20\\0.19 & x = 45\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 38th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0506500222

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.09 & x = 0\\0.2 & x = 7\\0.01 & x = 21\\0.51 & x = 31\\0.19 & x = 41\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 64th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0758406613

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.05 & x = 2\\0.33 & x = 5\\0.04 & x = 21\\0.53 & x = 25\\0.05 & x = 30\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 80th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0632131874

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 8\\0.02 & x = 10\\0.31 & x = 28\\0.33 & x = 30\\0.17 & x = 43\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 44th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0569717004

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 11\\0.28 & x = 15\\0.23 & x = 17\\0.09 & x = 21\\0.28 & x = 24\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 52th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0590479977

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 8\\0.24 & x = 11\\0.05 & x = 16\\0.27 & x = 26\\0.27 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 89th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0111408527

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.36 & x = 9\\0.03 & x = 23\\0.04 & x = 29\\0.27 & x = 41\\0.3 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 63th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0351257399

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.64 & x = 1\\0.03 & x = 2\\0 & x = 22\\0.05 & x = 35\\0.28 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 66th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0543871182

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.01 & x = 3\\0.72 & x = 15\\0.1 & x = 19\\0.17 & x = 37\\0 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 77th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0016816512

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.04 & x = 3\\0.3 & x = 16\\0.45 & x = 25\\0.18 & x = 41\\0.03 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 6th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0291746806

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 8\\0.17 & x = 19\\0.37 & x = 35\\0.05 & x = 40\\0.29 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 88th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0638975051

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 0\\0.16 & x = 24\\0.2 & x = 30\\0.37 & x = 39\\0.1 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 23th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0517999320

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.02 & x = 7\\0.07 & x = 28\\0.25 & x = 30\\0.07 & x = 35\\0.59 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 55th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0718889244

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 8\\0.05 & x = 35\\0.27 & x = 36\\0.04 & x = 44\\0.52 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 96th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0571220144

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 8\\0.11 & x = 9\\0.64 & x = 11\\0.15 & x = 12\\0.03 & x = 16\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 91th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0675525932

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 17\\0.27 & x = 25\\0.28 & x = 46\\0.04 & x = 48\\0.24 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 49th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0851466330

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 1\\0.28 & x = 11\\0.04 & x = 19\\0.06 & x = 27\\0.5 & x = 44\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 29th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0649486695

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.2 & x = 7\\0.25 & x = 8\\0.29 & x = 10\\0.05 & x = 20\\0.21 & x = 31\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 46th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0851001275

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.13 & x = 8\\0.54 & x = 14\\0.22 & x = 29\\0.06 & x = 37\\0.05 & x = 38\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 8th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0245851640

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.23 & x = 10\\0.5 & x = 19\\0.12 & x = 23\\0.13 & x = 39\\0.02 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 22th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0980085713

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.09 & x = 5\\0.04 & x = 23\\0.32 & x = 28\\0.26 & x = 43\\0.29 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 85th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0418943165

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.06 & x = 6\\0.34 & x = 22\\0.37 & x = 31\\0.02 & x = 33\\0.21 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 62th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0040276508

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.03 & x = 7\\0.37 & x = 26\\0.17 & x = 31\\0.04 & x = 41\\0.39 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 80th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0797711141

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.6 & x = 2\\0.1 & x = 6\\0.02 & x = 8\\0.27 & x = 19\\0.01 & x = 27\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 16th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0445484998

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.1 & x = 0\\0.18 & x = 11\\0.26 & x = 29\\0.35 & x = 34\\0.11 & x = 36\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 99th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0683277259

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.15 & x = 6\\0.02 & x = 15\\0.39 & x = 24\\0.28 & x = 28\\0.16 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 63th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0657134015

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.23 & x = 4\\0.12 & x = 7\\0.01 & x = 13\\0.31 & x = 37\\0.33 & x = 39\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 97th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0389731140

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.27 & x = 19\\0.18 & x = 24\\0.04 & x = 28\\0.35 & x = 33\\0.16 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 89th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0844340952

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.4 & x = 10\\0.17 & x = 20\\0.1 & x = 27\\0.04 & x = 28\\0.29 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 89th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0193759052

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.56 & x = 16\\0.06 & x = 34\\0.17 & x = 37\\0.03 & x = 44\\0.18 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 9th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0520053210

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.28 & x = 16\\0.42 & x = 33\\0.1 & x = 40\\0.14 & x = 42\\0.06 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 44th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0275929214

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.06 & x = 0\\0.37 & x = 10\\0.26 & x = 17\\0.1 & x = 25\\0.21 & x = 44\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 3th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0468054494

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.31 & x = 8\\0.1 & x = 14\\0.42 & x = 18\\0 & x = 31\\0.17 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 39th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0783960197

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.1 & x = 22\\0.65 & x = 25\\0.15 & x = 26\\0.07 & x = 34\\0.03 & x = 41\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 64th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0843914792

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.11 & x = 7\\0.49 & x = 16\\0.21 & x = 35\\0.03 & x = 44\\0.16 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 61th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0579908952

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.4 & x = 9\\0.12 & x = 29\\0 & x = 31\\0.08 & x = 40\\0.4 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 24th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0464259137

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.03 & x = 31\\0.36 & x = 32\\0.15 & x = 36\\0.07 & x = 39\\0.39 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 93th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0299482452

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.23 & x = 16\\0.06 & x = 20\\0.22 & x = 39\\0.43 & x = 45\\0.06 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 41th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0528635731

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0 & x = 1\\0.01 & x = 4\\0.79 & x = 17\\0.1 & x = 36\\0.1 & x = 39\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 66th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0058560336

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.14 & x = 3\\0.48 & x = 11\\0.16 & x = 30\\0.12 & x = 48\\0.1 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 45th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0934655248

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 1\\0.32 & x = 3\\0.08 & x = 10\\0.29 & x = 11\\0.23 & x = 17\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 80th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0114464496

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.52 & x = 8\\0.02 & x = 12\\0.12 & x = 29\\0.31 & x = 36\\0.03 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 1th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0637708224

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.06 & x = 0\\0.24 & x = 21\\0.06 & x = 24\\0.18 & x = 36\\0.46 & x = 45\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 43th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0058224762

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 2\\0.13 & x = 4\\0.08 & x = 23\\0.43 & x = 35\\0.29 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 96th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0009894981

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.26 & x = 0\\0.26 & x = 16\\0.38 & x = 18\\0.01 & x = 38\\0.09 & x = 39\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 29th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0305864667

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.04 & x = 27\\0.06 & x = 35\\0.1 & x = 36\\0.74 & x = 41\\0.06 & x = 42\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 35th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0043287241

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 2\\0.27 & x = 10\\0.49 & x = 14\\0.1 & x = 47\\0.06 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 13th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0843584269

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.22 & x = 1\\0.04 & x = 3\\0.16 & x = 9\\0.2 & x = 19\\0.38 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 93th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0718093404

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.14 & x = 8\\0.04 & x = 15\\0.16 & x = 20\\0.45 & x = 21\\0.21 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 64th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0226380658

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.25 & x = 13\\0.21 & x = 16\\0.45 & x = 29\\0.08 & x = 35\\0.01 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 55th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0583193111

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 29\\0.31 & x = 38\\0.14 & x = 43\\0.12 & x = 44\\0.35 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 53th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0999579375

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0 & x = 15\\0.2 & x = 17\\0.03 & x = 35\\0.51 & x = 44\\0.26 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 62th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0801144056

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.23 & x = 14\\0.27 & x = 24\\0.02 & x = 26\\0.3 & x = 29\\0.18 & x = 45\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 11th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0539722613

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.5 & x = 0\\0.1 & x = 8\\0.23 & x = 13\\0.16 & x = 17\\0.01 & x = 19\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 60th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0672260548

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.16 & x = 2\\0.17 & x = 11\\0.21 & x = 23\\0.27 & x = 38\\0.19 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 51th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0834385464

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.47 & x = 13\\0.21 & x = 29\\0.15 & x = 35\\0.12 & x = 39\\0.05 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 92th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0592787623

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.06 & x = 2\\0.08 & x = 5\\0.1 & x = 13\\0.63 & x = 17\\0.13 & x = 23\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 83th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0870140921

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.36 & x = 13\\0.29 & x = 14\\0.18 & x = 24\\0.11 & x = 28\\0.06 & x = 40\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 68th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0810956393

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.32 & x = 4\\0.05 & x = 41\\0.49 & x = 44\\0.08 & x = 45\\0.06 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 86th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0148377977

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.27 & x = 5\\0.14 & x = 6\\0.06 & x = 9\\0.44 & x = 40\\0.09 & x = 41\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 64th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0580309142

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.37 & x = 2\\0.05 & x = 8\\0.12 & x = 13\\0.16 & x = 21\\0.3 & x = 35\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 61th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0125851323

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.62 & x = 5\\0.12 & x = 8\\0.2 & x = 14\\0.05 & x = 17\\0.01 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 57th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0292538163

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.1 & x = 9\\0.09 & x = 13\\0.07 & x = 18\\0.6 & x = 25\\0.14 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 69th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0691858441

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.43 & x = 6\\0.07 & x = 12\\0.01 & x = 23\\0.31 & x = 32\\0.18 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 56th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0288503155

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 10\\0.49 & x = 39\\0.32 & x = 40\\0.06 & x = 48\\0.05 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 19th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0221620870

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.27 & x = 7\\0.03 & x = 16\\0.36 & x = 22\\0.02 & x = 29\\0.32 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 63th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0577318833

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.09 & x = 4\\0.03 & x = 11\\0.03 & x = 12\\0.37 & x = 36\\0.48 & x = 42\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 22th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0037014528

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0 & x = 16\\0.34 & x = 23\\0.36 & x = 26\\0.19 & x = 48\\0.11 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 84th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0968563652

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.14 & x = 5\\0.11 & x = 8\\0.02 & x = 15\\0.33 & x = 22\\0.4 & x = 43\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 65th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0762930171

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 5\\0.09 & x = 21\\0.46 & x = 23\\0.36 & x = 36\\0.01 & x = 38\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 59th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0092306611

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 7\\0.41 & x = 9\\0.1 & x = 14\\0.37 & x = 17\\0 & x = 28\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 67th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0296861126

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.63 & x = 9\\0.18 & x = 22\\0 & x = 28\\0.14 & x = 30\\0.05 & x = 48\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 91th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0998751028

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 15\\0.06 & x = 22\\0.18 & x = 26\\0.45 & x = 28\\0.24 & x = 29\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 41th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0488896442

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.11 & x = 0\\0.16 & x = 2\\0.35 & x = 6\\0.17 & x = 23\\0.21 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 98th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0075654524

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.02 & x = 14\\0.16 & x = 27\\0.18 & x = 32\\0.57 & x = 39\\0.07 & x = 43\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 27th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0482779970

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.08 & x = 5\\0.24 & x = 11\\0.52 & x = 25\\0.13 & x = 32\\0.03 & x = 37\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 73th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0603133540

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 6\\0.23 & x = 15\\0.21 & x = 21\\0.34 & x = 30\\0.05 & x = 31\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 60th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0457841232

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.4 & x = 1\\0.37 & x = 28\\0.04 & x = 29\\0.04 & x = 32\\0.15 & x = 38\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 76th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0016162131

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.54 & x = 7\\0.01 & x = 8\\0.07 & x = 10\\0.07 & x = 37\\0.31 & x = 47\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 3th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0779487815

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.12 & x = 5\\0.57 & x = 17\\0.11 & x = 18\\0.14 & x = 26\\0.06 & x = 35\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 60th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0048167221

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.05 & x = 8\\0.09 & x = 14\\0.28 & x = 23\\0.46 & x = 39\\0.12 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 78th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0751801113

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.07 & x = 15\\0.15 & x = 19\\0.27 & x = 28\\0.31 & x = 41\\0.2 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 14th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0650185421

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.22 & x = 5\\0.05 & x = 15\\0.14 & x = 17\\0.28 & x = 19\\0.31 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 69th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0232501599

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.34 & x = 3\\0.27 & x = 8\\0.09 & x = 14\\0.1 & x = 27\\0.2 & x = 31\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 49th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0236695759

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.21 & x = 2\\0.09 & x = 3\\0.58 & x = 24\\0.07 & x = 25\\0.05 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 59th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0036089058

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.03 & x = 11\\0.06 & x = 20\\0.14 & x = 24\\0.6 & x = 25\\0.17 & x = 46\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 93th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0406401040

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.36 & x = 0\\0.47 & x = 7\\0.08 & x = 9\\0.04 & x = 14\\0.05 & x = 16\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 18th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0385188928

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.42 & x = 2\\0.15 & x = 3\\0.02 & x = 10\\0.14 & x = 44\\0.27 & x = 49\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 4th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0301308155

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.17 & x = 8\\0.5 & x = 20\\0.12 & x = 23\\0.07 & x = 30\\0.14 & x = 50\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 48th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0283878808

The following is the probability mass function for a random variable \(X\), \[p_X(x) = \begin{cases}0.22 & x = 2\\0.34 & x = 4\\0.26 & x = 10\\0.18 & x = 12\\0 & x = 31\end{cases}.\]

1. What is \(E[X]\)?
2. What is the median of \(X\)?
3. What is the mode of \(X\)? (Note: select the smallest value for the mode, if multiple modes exist).
4. What is the 91th percentile of \(X\)?
5. What is the range of \(X\)?
6. What is the variance of \(X\)?
7. What is the mean absolute deviation of \(X\)?
8. What is the standard deviation of \(X\)?
9. What is the interquartile range of \(X\)?

Question ID: 0793848529

---

1. As a general rule when learning it is often helpful to consider exercises of discovery. That is, try to determine why particular definitions are the way that they are, or where they have from.

2. You should picture the owner of this fictitious cupcake store as a giant, multinational, faceless corporation. A corporation that seems to take pleasure in stepping on the local businesses. That way, as Charles and Sadie try to fight back, we can remain on their side!

3. When multiple modes exist, convention tends to report the set of all of the modes. In the equally likely outcome model, this is the entire support for the random variable, and as a result, the mode is exactly the probability mass function. There is no summary provided.

4. You will find many introductory sources that say that you should always use the median when you are concerned with extreme values. This is a great oversimplification of the truth, and points to a general rule in Statistics: there are very few general rules. The guidance comes from the fact that often extreme values skew our perceptions of the underlying truth. While this may be true in general, it is not true often enough to warrant being given as universal guidance.

5. An insurance company ignoring these massive claims would almost certainly go out of business very, very quickly.

6. While less commonly applied than the simple average, a weighted average is familiar to most students for a crucial purpose: grade calculations. If you view the weight of each item in a course as a probability mass, and the grade you scored as the value, then your final grade in the course is exactly the expected value of this distribution.

7. The data are one consideration for which measure to use, but not the only one (and not the most important one).

8. and an attractive one, but a mistake nonetheless.

9. Some statisticians dislike this name. I find it to be rather cute.

10. For instance, suppose you are betting a certain amount on the results of a coin toss, or that you are taking a multiple choice test that gives \(2\) points for a correct answer.

11. Try working this out!

12. And, as a result, \(P(X > m) = 0.5\) as well.

13. Note that, when dealing with discrete random variables, it may not be possible to find a value \(\zeta(p)\) such that \(P(X \leq \zeta(p)) = p\) exactly. Instead, we typically define the percentile here to be such that \(P(X < \zeta(p)) < p \leq P(X \leq \zeta(p))\).

14. The reasons for this are plentiful, but generally squares are easier to handle than absolute values, and as a result become more natural quantities to consider.

15. This seems to be an oxymoron, but it is perfectly well defined.